目录
[一、MPC 最核心的思想(必须先理解)](#一、MPC 最核心的思想(必须先理解))
[2.5)滚动求解(Receding Horizon)](#2.5)滚动求解(Receding Horizon))
[二、为什么预测区间较控制区间多 1?](#二、为什么预测区间较控制区间多 1?)
[三、MPC 状态预测:以 4 步预测为例(Np=4)](#三、MPC 状态预测:以 4 步预测为例(Np=4))
[四、构造大向量 X 和 U](#四、构造大向量 X 和 U)
[五、得到经典 MPC 预测矩阵:X = Fx + GU](#五、得到经典 MPC 预测矩阵:X = Fx + GU)
[1)F 矩阵(预测初始状态的贡献)](#1)F 矩阵(预测初始状态的贡献))
[2)G 矩阵(控制量对未来状态的影响)](#2)G 矩阵(控制量对未来状态的影响))
[六、X = F xₖ + G U 在时间轴上的含义](#六、X = F xₖ + G U 在时间轴上的含义)
[1)第一次优化(在时刻 k)](#1)第一次优化(在时刻 k))
[2)第二次优化(在时刻 k+1)](#2)第二次优化(在时刻 k+1))
[九、MPC 代价函数构建与 QP 优化问题形成过程](#九、MPC 代价函数构建与 QP 优化问题形成过程)
[1)构造 MPC 代价函数 J](#1)构造 MPC 代价函数 J)
[2)将 X = F xₖ + G U 代入代价函数](#2)将 X = F xₖ + G U 代入代价函数)
[3)最终 QP 形式(直接给 qpOASES 求解)](#3)最终 QP 形式(直接给 qpOASES 求解))
[十、代价函数二次型展开、QP 核心矩阵 H、f 和有/无约束QP的二次型代价函数梯度求解手推步骤](#十、代价函数二次型展开、QP 核心矩阵 H、f 和有/无约束QP的二次型代价函数梯度求解手推步骤)
[十一、QP 求解 → 得到最优控制序列 U*](#十一、QP 求解 → 得到最优控制序列 U*)
MPC(模型预测控制)概念
模型预测控制(Model Predictive Control,MPC)是一种 基于模型的优化控制方法 。
它不是像 PID 那样"根据当前误差给输出",
也不是像纯追踪(Pure Pursuit)、Stanley 那样用几何关系求转角。
MPC 是用"未来好几步"的预测来决定"现在该怎么做"。
核心思想只有一句话:
在未来 N 步时间上,让系统的状态 X 尽量跟随参考轨迹 Xref,
并找到一串最优控制量 U,使代价最小、约束满足。
因此,MPC 本质上是:
"控制 + 预测 + 规划 + 优化" 的统一框架
前言
模型预测控制(Model Predictive Control, MPC)是现代自动驾驶、AGV、无人机中最主流的轨迹跟踪控制器。
然而,很多人只会用,却不知道:
-
MPC 的未来状态是怎么预测的?
-
控制输入 uk 是从哪里"求"出来的?
-
为什么预测区间总是比控制区间多 1?
-
MPC 如何变成一个二次规划(QP)问题?
本文将一步步从 离散模型 → 预测矩阵 → 代价函数 → QP 优化问题 → 得到最优控制量 整体推导,让你真正理解 MPC 的底层数学结构。
一、MPC 最核心的思想(必须先理解)
1)关键思想:
在 MPC 中:
uₖ、uₖ₊₁、uₖ₊₂......都不是提前设定的,
而是优化器求解出来的最优控制序列(决策变量)。
我们并不是给出一个 uk,然后预测未来状态。
而是:
2)步骤:
2.1)MPC未来N步的控制量
MPC 会把未来 N 步的控制量
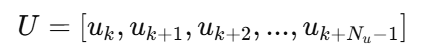
全部当成 未知变量。
2.2)构建优化目标:
未来轨迹误差最小+控制量最小+满足约束
2.3)二次规划(QP)求解器
最终通过 二次规划(QP)求解器 求出一整串最优控制量序列 U*。
2.4)执行第一个控制量
MPC 每次只执行第一个控制量:
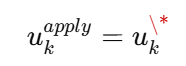
2.5)滚动求解(Receding Horizon)
然后进入下一时刻,滚动求解(Receding Horizon)。
二、为什么预测区间较控制区间多 1?
MPC 的预测模型:
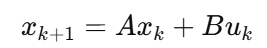
结构如下:
css
时间步: k k+1 k+2 k+3 k+4
|---------|----------|----------|----------|
状态: x_k x_{k+1} x_{k+2} x_{k+3} x_{k+4}
↑ ↑ ↑ ↑
控制: u_k u_{k+1} u_{k+2} u_{k+3}
(第1步) (第2步) (第3步) (第4步)
预测区间: [-------------- Np = 4 步状态预测 --------------]
控制区间: [----------- Nu = 4 个控制量 -----------]可以看到:
-
状态点:xₖ, xₖ₊₁, xₖ₊₂, xₖ₊₃, xₖ₊₄ → 5 个
-
控制量:uₖ, uₖ₊₁, uₖ₊₂, uₖ₊₃ → 4 个
所以预测区间状态数量 = 控制区间 + 1 ,
本质原因就是:状态是"节点",控制是"节点之间的边"。
三、MPC 状态预测:以 4 步预测为例(Np=4)
MPC离散线性模型:
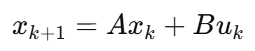
逐步展开:
第 1 步:
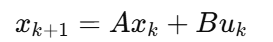
第 2 步:
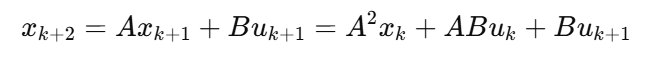
第 3 步:
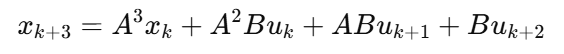
第 4 步:
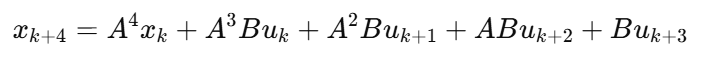
四、构造大向量 X 和 U
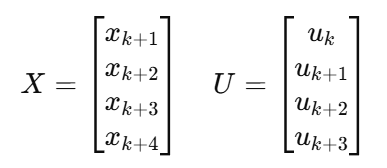
五、得到经典 MPC 预测矩阵:X = Fx + GU
1)F 矩阵(预测初始状态的贡献)
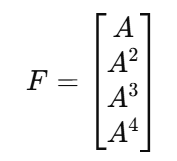
2)G 矩阵(控制量对未来状态的影响)
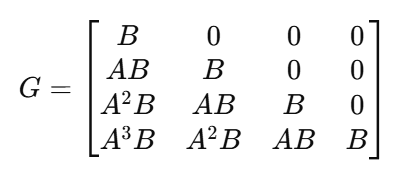
最终预测公式:
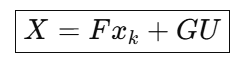
这是 MPC 的最核心公式之一。
六、X = F xₖ + G U 在时间轴上的含义
上一节我们推导了:
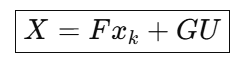
在时间轴上,可以把 X 和 U 理解为:
css
X = [x_{k+1}, x_{k+2}, x_{k+3}, x_{k+4}]^T
U = [u_k, u_{k+1}, u_{k+2}, u_{k+3}]^T此时:
-
F 决定:如果不给控制量(U=0),仅靠 A 演化,xₖ 会怎样传播到未来 4 步
-
G 决定:每一个控制量 uₖ, uₖ₊₁, uₖ₊₂, uₖ₊₃ 是如何叠加影响未来每个 x 的
你可以这样理解矩阵 G:
css
G =
[ B 0 0 0 ] → 只影响 x_{k+1}
[ A B B 0 0 ] → u_k 影响 x_{k+2},u_{k+1} 也影响 x_{k+2}
[ A^2 B A B B 0 ] → 三个控制依次累积影响 x_{k+3}
[ A^3 B A^2 B A B B ] → 四个控制依次累积影响 x_{k+4}在时间轴上的直观图:
css
x_k --u_k--> x_{k+1} --u_{k+1}--> x_{k+2} --u_{k+2}--> x_{k+3} --u_{k+3}--> x_{k+4}
u_k 影响: x_{k+1}, x_{k+2}, x_{k+3}, x_{k+4}
u_{k+1} 影响: x_{k+2}, x_{k+3}, x_{k+4}
u_{k+2} 影响: x_{k+3}, x_{k+4}
u_{k+3} 影响: x_{k+4}这就是 G 矩阵下三角结构 的直观含义:
越早施加的控制,对未来状态产生越多影响。
七、滚动优化
MPC 不是只算一次 U 就完事了,而是每个采样时刻都要重新优化一次。
1)第一次优化(在时刻 k)
css
当前真实状态:x_k 已知
优化得到:
U* = [u_k*, u_{k+1}*, u_{k+2}*, u_{k+3}*]
只执行第一个控制量:
u_k^{apply} = u_k*时间轴视图:
css
(第 1 次优化)
时间: k k+1 k+2 k+3 k+4
|---------|----------|----------|----------|
状态: x_k x_{k+1} x_{k+2} x_{k+3} x_{k+4}
控制: u_k* u_{k+1}* u_{k+2}* u_{k+3}*
↑
实际执行的只有这个2)第二次优化(在时刻 k+1)
车按照 u_k* 运行到新状态 xₖ₊₁,
现在新的初始状态是 xₖ₊₁,重新算一遍新的最优控制序列:
css
当前真实状态:x_{k+1} 已知
再次优化得到:
U_new* = [u_{k+1,new}*, u_{k+2,new}*, u_{k+3,new}*, u_{k+4,new}*]
只执行:
u_{k+1}^{apply} = u_{k+1,new}*此时时间轴从 k+1 开始"重新切一块"预测窗口:
css
(第 2 次优化:预测窗口右移一格)
时间: k+1 k+2 k+3 k+4 k+5
|----------|----------|----------|----------|
状态: x_{k+1} x_{k+2} x_{k+3} x_{k+4} x_{k+5}
控制: u_{k+1} u_{k+2} u_{k+3} u_{k+4}
↑
现在只执行它3)关键点:
-
每次优化 "看向未来好几步"
-
但只执行第一个控制量
-
下一次再重新用最新的状态出发,重新规划
这就是 " 滚动时域优化(Receding Horizon)" 的精髓。
八、状态预测模型&离散矩阵手推步骤
九、MPC 代价函数构建与 QP 优化问题形成过程
1)构造 MPC 代价函数 J
常见代价函数:
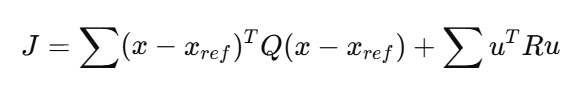
写成矩阵形式:
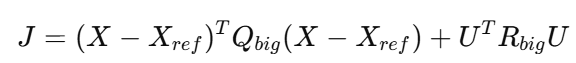
其中:
-
Qbig:4 次对角重复 Q
-
Rbig:4 次对角重复 R
2)将 X = F xₖ + G U 代入代价函数
代入后:
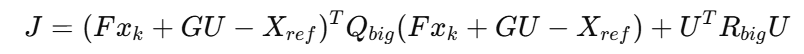
展开 → 整理 → 得到标准 QP 形式:
3)最终 QP 形式(直接给 qpOASES 求解)
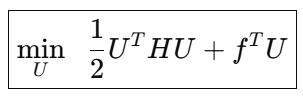
其中:
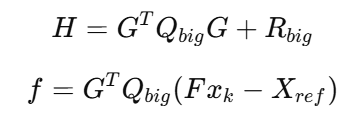
常数项被省略(不影响最优解)。
4)加入约束
控制约束:
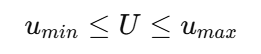
状态约束(可选):
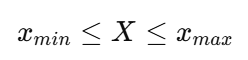
转化为:
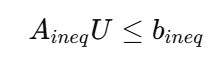
十、代价函数二次型展开、QP 核心矩阵 H、f 和有/无约束QP的二次型代价函数梯度求解手推步骤
十一、QP 求解 → 得到最优控制序列 U*
QP 求解器输出:

也就是 控制区间长度 Nu(控制时域)内的所有控制量。
MPC 实际执行:
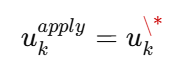
然后更新状态

接着进入下一轮优化,继续求新的:
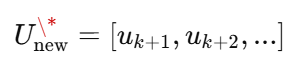
进入下一时刻重新求解:滚动优化(Receding Horizon)
十二、MPC理论步骤总结
① 离散状态模型
② 逐步预测 4 步
③ 得到矩阵形式:X = F x + G U
④ 套入 Q,R 得到代价函数 J
⑤ 推成标准 QP(H, f)
⑥ 加入(in)eq 约束
⑦ 丢给 qpOASES → 得到最优控制量序列
⑧ 执行第一步 → 滚动优化
十三、全文总结
-
MPC 中的控制量不是设定的,是优化器求出来的
-
预测区间 = 控制区间 + 1(状态是节点,控制量是边)
-
经典预测公式
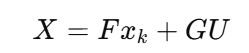
- 代价函数 J 可写成标准二次规划(QP):
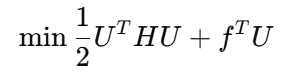
- QP 求解器输出整串控制序列,只执行第一个控制量,之后滚动优化。

