Provable Robust Watermarking for AI-Generated Text：给大模型文字“打上隐形指纹”

1. 论文基本信息

-　标题：Provable Robust Watermarking for AI-Generated Text

-　作者：Xuandong Zhao, Prabhanjan Ananth, Lei Li, Yu-Xiang Wang

-　机构：UC Santa Barbara

-　年份：2023（arXiv:2306.17439v2）

-　研究方向 ：大语言模型（LLM）、文本水印、鲁棒检测、理论保证、对抗攻击

-　核心方法名词：Unigram-Watermark、K-gram watermark、green list / red list、z-score 检测统计量、Renyi 散度、Type I/II error、edit distance

2. 前言

论文解决了什么问题？

　　**这篇论文想解决的是：如何给大模型生成的文本加"隐形水印"，并且在用户后续各种编辑、同义改写之后，仍然能可靠地检测出来，而且有严格的数学保证。**现有很多检测方法要么纯靠统计特征、容易被分布漂移和攻击打爆，要么水印方案没有清晰的鲁棒性分析。作者给出了一套形式化的"LLM 文本水印理论框架"，把"质量、误报率、漏报率、抗编辑攻击"全部写成可证明的性质。
有何历史意义和性能突破？

　　论文在一个非常关键的点上前进了一步：第一次对"统计型文本水印"给出了针对任意编辑攻击的可证明鲁棒性保证 ，并且在实验上比之前最有代表性的软水印方案（Kirchenbauer et al. 2023, 下文简称 KGW+23）更抗 paraphrase、更抗随机修改，同时几乎不损伤文本质量。作者还证明：当文本足够长且多样时，误报、漏报的概率会随长度指数级下降。
为什么值得写一篇解读？

　　第一，这篇工作关乎 AI 生成内容溯源，对学术诚信、内容审核、数据去污染都很现实。第二，它把水印问题放进了一个清晰的数学框架里，对之后的研究会是一个"基准范式"。第三，方法本身设计很简单（几乎只是在 logits 上加常数），却有 DP 风格的理论分析，非常有"性价比"。所以很值得把它好好拆开讲一讲。

3. 基础概念铺垫

　　大语言模型与概率分布。

　　一个 LLM（比如 GPT、LLaMA）在给定提示词 x 时，其实是在对下一 token 的分布做预测：对词表里每个 token 都给出一个概率。论文里记作：第 t 个位置、在当前上下文下生成 token v 的概率。整段文本就是一次次从这些分布中采样的结果。

　　什么是"文本水印"？

　　你可以把它理解成：在不影响读者体验的前提下，偷偷偏好"某一批词"，让这些词在生成文本中略微"超频出现"，然后在检测时再把这批词找出来，看它们是不是"多得有点过头"。

　　这批被偏好的词，就是所谓的 绿色列表（green list） ；其他词就是 红色列表（red list） 。水印的秘密就藏在"哪些 token 是绿的"这个划分里，这个划分由密钥 k 决定。

　　Type I / Type II 错误。

　　- Type I：把没带水印的文本错判成"有水印"（误报）。

　　- Type II：把实际带水印的文本错判成"没水印"（漏报）。

　　一个好的方案要同时控制这两个错误率，而且最好能说清楚：它们是怎么随文本长度变化的。

　　编辑距离（edit distance）。

　　论文用 Levenshtein 风格的编辑距离：把一段文本 y 变成另一段文本 z，需要多少次 token 级的"插入、删除、替换"。作者把"攻击者的改写代价"形式化成这个距离，并在这个度量下给出"要想躲过检测，你至少要改掉多少个 token"的下界。

　　z-score 检测统计量。

　　最核心的检测指标是：

其中是文本里落在 green list 的 token 数，(n) 是总长度，是 green list 所占词表比例。直观上，z-score 越大，说明"绿色 token 比正常随机情况多很多"，越可能是带水印的文本。

4. 历史背景与前置技术

　　大模型文本溯源，之前主要有两条路线：

事后检测（post-hoc detectors）

　　这类方法试图"仅从文本本身"判断是不是机器写的，比如 GLTR 看 token 概率是不是太"平滑"，DetectGPT 看 log-prob 曲率，或者训练分类器直接区分人类 vs 模型。

　　问题是：

　　- 模型越强，生成文本越像人，统计特征趋同 ；

　　- 模型一换、prompt 一变、或者被 paraphrase 一下，检测器就容易翻车；

　　- 还有对非母语者的偏见问题。
主动水印（watermarking）

　　另一条思路是：在生成时就埋好"暗号" ，比如 Kirchenbauer et al. (2023) 的 soft watermark：

　　- 根据前 K-1 个 token 的前缀，动态地 把词表随机分成 green/red 两组；

　　- 然后在 green 组上略微提高概率，使得生成结果总体更偏爱 green token；

　　- 检测时，对给定文本和同样的前缀规则，统计 green token 的数量，做假设检验。

　　KGW+23 这套 K-gram watermark 很优雅，但存在一个现实问题：

　　- 后处理敏感 ：如果有人对水过的文本做同义替换、paraphrase、删词，这种"依赖前缀决定分组"的设计会使 green/red 的判定完全被打乱，检测能力急剧下降；

　　- 另一方面，它的鲁棒性分析有一些不够系统、偏经验。

　　与此同时，还有一些 密码学式水印（Aaronson 2023, Christ et al. 2023），追求的是"对任何多项式时间攻击都是安全的"，但往往实现复杂、未必能直接落地在现有 LLM API 上。

　　这篇论文站的位置很明确：

　　- 沿用 统计型 K-gram watermark 的基本思路；

　　- 但选择 最简单的 K=1 版本（Unigram-Watermark） ，用固定的 green/red 划分；

　　- 然后从质量、误报、漏报、编辑鲁棒性等方面给出 系统的理论分析 + 实证验证。

5. 论文核心贡献

　　如果用一段话来概括，这篇论文的核心贡献大致是：在几乎不改动原始 LLM 推理逻辑的前提下，通过对词表做一次固定随机划分，并在 green token 上加一个统一的 logit 偏置，就构造出一个简单到"有点可疑"的文本水印方案；随后，作者用差分隐私工具箱和集中不等式，证明了这个水印在生成质量、检验准确性和对任意编辑攻击的鲁棒性上，都达到了可以写成定理的程度------同时，还在多个公开模型和数据集上展示它比现有软水印更扛 paraphrase、更扛编辑，几乎不损失困惑度和人工感受。

6. 方法详解（Unigram-Watermark）

6.1 问题形式化：什么叫"LLM 水印方案"？

　　作者先给了一个比较抽象但很有用的定义，把"一个水印方案"拆成两个算法：

Watermark(M) ：

　　输入原始语言模型 (M)，输出：

　　1. 一个"加了水印的模型" ；

　　2. 一个"检测密钥" (k)。

　　这两者合在一起，就定义了"这家模型厂商的水印风格"。
Detect(k, y) ：

　　输入密钥 (k) 和一段文本 (y)，输出 1 或 0：

　　- 1：认为是生成的（带水印）；

　　- 0：认为不是。

　　这个定义还要求水印满足三类性质：

质量保证（ω-Quality）

　　在任意给定 prompt 和前缀下，原模型输出分布是，水印模型是。

　　要求某个概率距离，也就是说：

　　> 加水印并不会"把模型变成另一个人"，它在每个 token 级别都和原模型保持很近。
Type I 错误控制（No false positives）

　　对于任意固定文本 y （只要它是在不知道密钥的情况下生成的），

　　误报率。
Type II 错误控制（No false negatives）

　　对于由在 prompt x 下生成的文本，漏报率。
安全性（Security property）

　　这里是最有趣的：作者要求，对于任何攻击者，把生成的文本 y 改成：

　　要么检测器仍然判 1，要么 编辑距离 ED(y, y_A) 必须至少达到某个下界。

　　直觉是：

　　> 想抹掉水印，就得真动刀子，不是"小修小改"就能蒙混过关的。

6.2 Unigram-Watermark：生成端算法（Algorithm 1）

随机划分词表

　　- 用随机数生成器和密钥 k ，把词表 (V) 划成两部分：

　　　- green list (G)：大小约为；

　　　- red list 。

　　- 这里的是一个超参数，比如 1/3 或 1/2。
修改 logits

　　- 对于任意生成步骤 t ，原模型给出 logits 向量；

　　- 水印模型把 green token 的 logit 统一加上一个常数：

　　- 然后再照常做 softmax 采样下一 token。
输出

　　- 返回水印模型 () 和密钥 k。

　　这就是 Unigram-Watermark：K=1 的 K-gram watermark。

　　之前 K≥2 的方案会根据"前缀"动态决定 green/red 列表；这里则是 前缀无关的固定划分，这也是它名字中 "Unigram" 的由来。

　　参数含义：

()：green list 占词表的比例。

　　- 越小：green token 越稀有，检测信号越强，但会对生成分布施加更大偏置。
()：logit 偏置强度。

　　- 越大：水印越"浓"，更容易检测，但更有可能损伤文本质量。

　　作者实验里常用配置是 (=2.0, =0.5)。

6.3 Unigram-Watermark：检测端算法（Algorithm 2）

　　检测器做的事也非常直接：

恢复 green list

　　- 用密钥 k 在本地重新生成 green list (G)。
数一数"绿词"

　　- 对 suspect 文本，统计
计算 z-score

　　- 直观理解：

　　　- 如果文本是"随机"用 green/red（比如人类写的），则期望约为，z-score 接近 0；

　　　- 如果是带水印文本，会倾向于多选 green token，会偏大，z-score 很可能显著 > 0。

阈值判断

　　- 选一个阈值（实验里经验值大概在 6 左右）；

　　- 若则判"带水印"，否则判"无水印"。

　　一个关键点是：这个检测器完全不需要访问原始模型或生成时的 prompt，只需要词表划分的密钥。

6.4 质量保证：水印对生成分布影响有多大？

　　作者先从最基本的问题入手：往 logits 上加个 δ，会不会把模型搞坏？

　　用到的主定理（Theorem 3.1）：

对任意步 t 、任意上下文 h ，

　　- 原分布是 ()，

　　- 水印分布是 ()。
他们证明了：对所有 Rényi 散度（包含 KL、χ²、Hellinger、Total Variation 等）的距离都满足：

　　直觉：

　　- 如果 δ 很小，这个 bound 大约是 ()；

　　- 也就是说，每一步的概率分布变化是二阶小的，整体上不会把模型"拉走太远"。

　　通过 DP 里的 composition 定理，作者还得到：整段长度 n 的文本分布之间的 KL 散度是 线性累积 的 ()。当 δ 适中、文本长度不是极端巨大时，水印模型生成的句子统计上仍然很接近原模型。

　　这给了一个非常硬的结论：Unigram-Watermark 满足他们定义中的 ω-Quality 要求。

6.5 Type I 错误：为什么不会"冤枉"人类文本？

　　Type I 错误是"没水印但被判有水印"。

　　作者证明的主要结果（Theorem 3.3 / C.4）可以粗暴概括为：

对于任意固定文本 y ，只要这个文本 不是为了配合密钥特意构造的 ，

　　- 也就是它的生成过程和词表划分 G 独立；

　　- 那么，它的 z-score (z_y) 在绝大多数情况下都处在一个 (O(1)) 的范围内。
更具体地：

　　- 定义：

　　　- ：文本中出现次数最多的那个 token 的计数；

　　　- ：大致刻画整个文本的"多样性"；

　　- 那么可以给出一个上界：

　　- 只要文本足够多样（不会是"goal goal goal..."那种），这个上界就是常数量级。

　　于是，检测器可以这样做：

给定一个期望的误报率（比如 1%）；
根据 y 的多样性参数算出一个 自适应门限 ；
证明表明：在这个 τ 下，Type I 错误概率 ≤ α，并且随着 τ 增大指数级下降。

　　这说明：只要阈值选得合理，人类文本以及无水印机器文本几乎不会被误判成"带水印"。

6.6 Type II 错误：水印文本为什么"躲不过去"？

　　这里难度就大得多了：要保证"只要是我们自己的水印文本，就几乎一定能检测出来"。

　　作者先提出两个假设：

On-average high entropy（平均高熵）

　　- 简单说，就是：在生成过程中，各步的 token 分布不能总是"特别尖锐"；

　　- 如果模型每一步都几乎确定要选某个 token（比如按指令一遍遍输出同一个词），那无论怎么加水印，都很难改变"绿词计数"的统计性质。
Homophily（同质性）假设

　　- 大意是：如果在某一步多生成了 green token，那么在未来的步骤里，green token 的概率不会"被平均拉下来"，平均意义上反而不会更少。

　　- 这对大多数正常的语言生成是合理的：你写了一个词，往往会在后面继续围绕类似的内容展开。

　　在这两个假设下，他们证明（Theorem 3.5 / C.13）：

对于水印模型生成的文本 y，

　　也就是 z-score 会随 (\sqrt{n}) 线性增长；
与前面 Type I 用到的结果对比：

　　- 无水印文本：是 (O(1))；

　　- 带水印文本：。

　　这样一来，就出现了一个非常漂亮的情况：

只要文本长度 n 足够大（大约到 (O(1/\delta^2)) 量级），就可以在一个很宽的阈值区间里做到"误报率和漏报率都指数级小"。

　　换句话说：越长的文本、水印越"稳"。

6.7 安全性：面对编辑攻击有多"硬"？

　　最关键的安全性结果是 Theorem 3.7：

设 y 是水印文本，攻击者把它改成 u，编辑距离为；
记它们的 z-score 分别为；
定理给出下界：

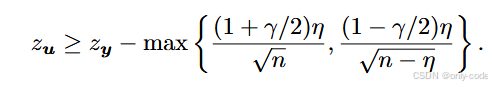
　　直觉解读：

每做一个编辑操作（插入 / 删除 / 替换），最多只能把一个 green token 换成 red 或反过来；
整体 z-score 的变化被严格地限制在这个量级；
而刚刚 Type II 的结果告诉我们：

　　- 原始；

　　- 所以只要没到某个线性级别，仍然高得离谱，检测依旧很容易。

　　论文里甚至指出：对 Unigram-Watermark 来说，要想彻底抹平水印，需要的编辑数量是 O(n) 的，也就是要改掉文本的一大半。

　　他们还和 KGW+23 的 K≥2 watermark 做了对比：在同样的分析框架下，Unigram-Watermark 至少"强一倍"------也就是说，对同样的编辑预算，Unigram 的 z-score 掉得更少。

6.8 其他细节：K 的选择、攻击者能否学出 green list？

　　作者对 "为什么选择 K=1，而不是 K≥2" 做了一些讨论：

选择 K=1 的好处：

　　- 对编辑/截断/乱序攻击更鲁棒 ：因为 green list 是固定的，不依赖前缀；

　　- 很多攻击（比如"在每个 token 前插一个 emoji"）会完全摧毁 K≥2 的分组逻辑，但对 K=1 几乎无影响。
代价：

　　- 攻击者如果能收集大量带水印文本，似乎可以从频率分布里估计出哪些 token 倾向于在水印文本中更常出现，也就是"学出 green list"；

　　- 这就带来了所谓的 "鲁棒性 vs 可学习性"权衡。

　　在附录 B.4 里，作者模拟了这种 white-box 攻击：

攻击者从水印模型和"人类文本"各采样数十万 token，算出每个 token 在水印文本里比在人类文本里频率高多少；
然后把正差值的 token 当作 green list。

　　结果显示：

即便如此，估计出来的 green list 仍然相当不准；
即使假设攻击者 完全知道真实的 green list ，试图通过同义词替换把 green token 换成 red token，也会造成 文本困惑度大幅上升，质量明显下降，而检测 AUC 仍然不低。

　　这说明：在现实设定下，"学出水印并抹除"的攻击并不轻松。

7. 实验结果与性能分析

7.1 实验设置

　　数据集与任务。

OpenGen：从 WikiText-103 中截取 3k 段两句的开头，后续 300 个 token 是人类写的 continuation。
LFQA：从 Reddit 抓取长问答，6 个领域各 500 条，总 3k 对，提问作为 prompt，回答作为人类长答案。

　　语言模型。

GPT2-XL（1.5B）、OPT-1.3B、LLaMA-7B 等三种公开模型；
使用 nucleus sampling 作为默认解码策略。

　　评价指标。

检测性能：在固定 FPR（1% 和 10%）下的 TPR、F1，以及 ROC-AUC；
文本质量 ：

　　- GPT-3 (text-davinci-003) 作为"oracle"算 perplexity；

　　- 众包工人（AMT）打 1--5 分的人工可读性评分。

　　所有模型都用统一的水印参数 (=2.0, =0.5)。

7.2 基本水印效果

论文 Table 1 -- 带/不带水印的 LLaMA-13B 文本对比

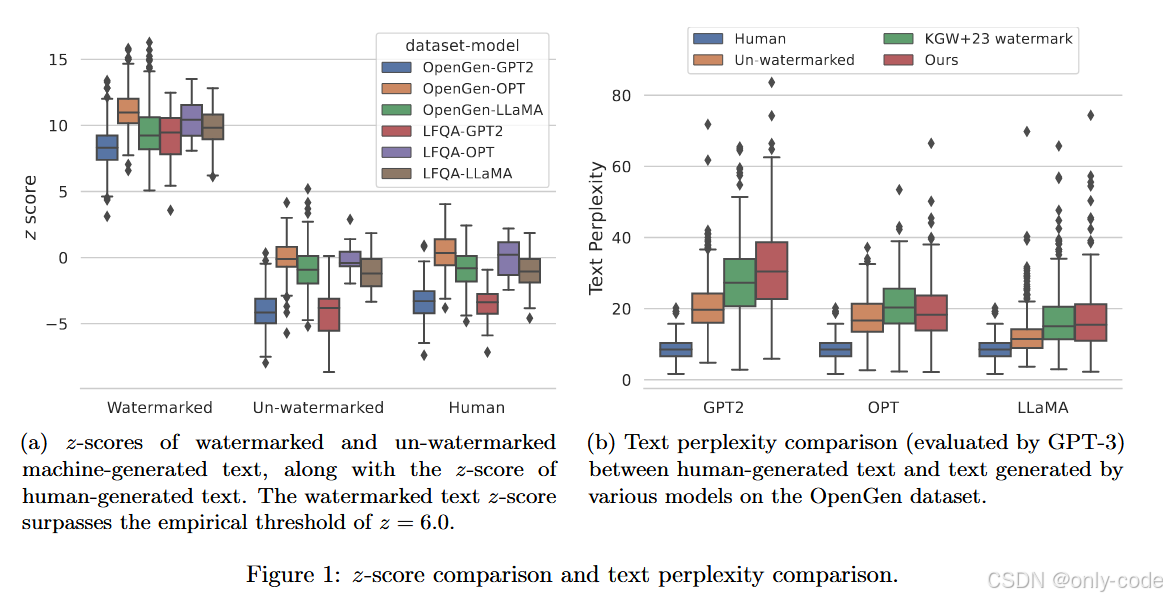
论文 Figure 1 -- z-score 与 perplexity 对比图

　　实验中，他们为每个模型、每种数据集生成 500 条带水印文本和 500 条无水印文本，并和对应的人类文本对比。

z-score 分布

　　- 对于带水印文本，z-score 往往远高于 6；

　　- 无水印机器文本和人类文本的 z-score 集中在 ~0 左右；

　　- 经验上，设阈值就能很好地区分有无水印。
困惑度与人工评价

　　- GPT-3 评估的 perplexity 显示：

　　　- 带水印文本的困惑度几乎和未水印文本一致；

　　　- 都略高于人类文本（因为 WikiText-103 与 GPT-3 的训练分布高度匹配）；

　　- 人工打分结果（在 LLaMA-7B + OpenGen 设定下）：

　　　- 无水印：3.660 ± 0.655

　　　- 有水印：3.665 ± 0.619

　　- 两者几乎完全齐平，说明水印不会显著妨碍可读性。

7.3 对 paraphrase 攻击的鲁棒性

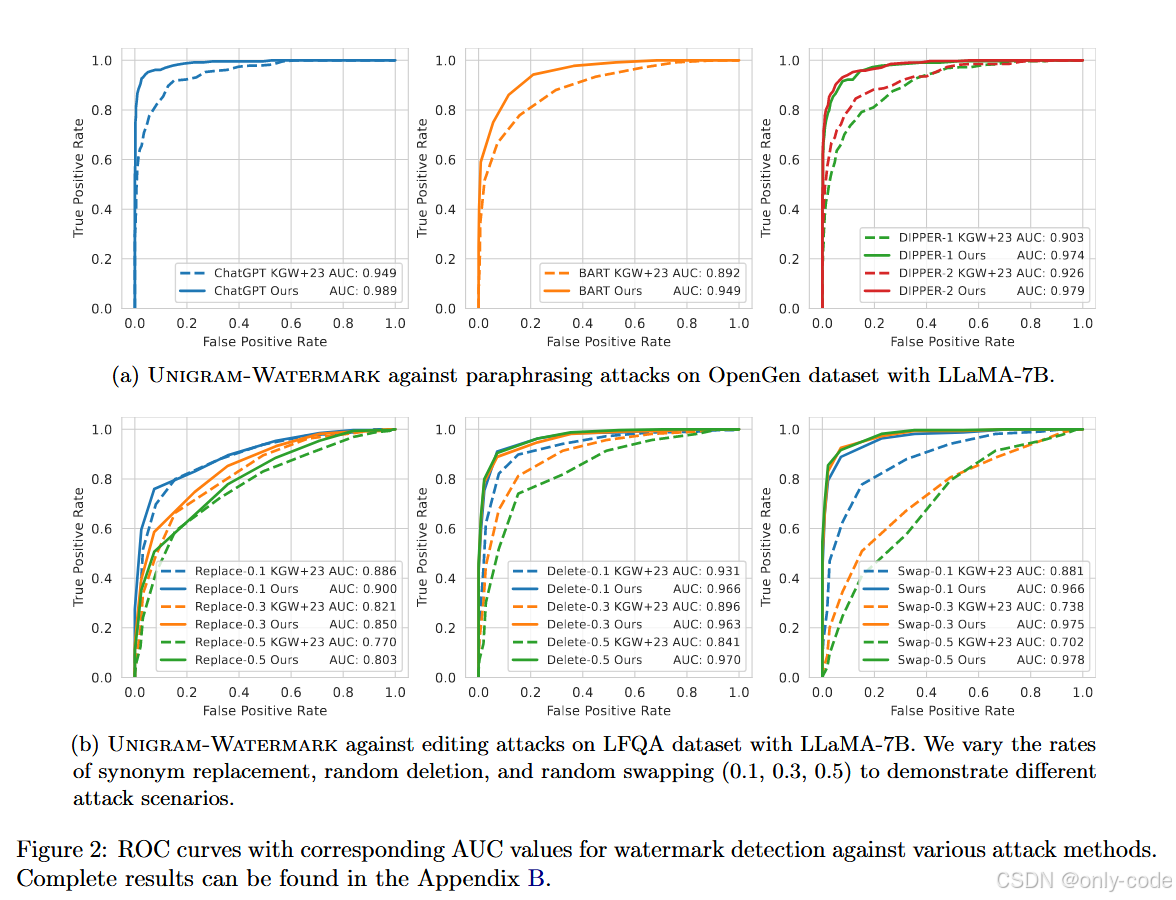
论文 Figure 2(a)、Figure 4(a) -- paraphrasing attack 下的 ROC 曲线　　

作者使用多种 paraphrase 模型攻击水印文本：

DIPPER-1 / DIPPER-2（后者生成更多样）；
ChatGPT API（通过"Rewrite the following paragraph"之类的 prompt）；
BART-large-cnn 做摘要，也视为一种强 paraphrase。

　　在 LLaMA-7B + OpenGen / LFQA 的设定下，与 KGW+23 对比（固定 FPR=1% 或 10%）：

ChatGPT 攻击 （OpenGen）：

　　- KGW+23：TPR ~0.56（1% FPR）、0.85（10% FPR）；

　　- Unigram：TPR ~0.87、0.96。
DIPPER / BART 攻击 ：

　　- 在所有组合下，Unigram 的 TPR 和 F1 都明显高于 KGW+23；

　　- 在 LFQA 上，某些设定下 Unigram 的 TPR 接近或超过 0.9，而 KGW+23 常停留在 0.7--0.8 左右。

　　再看 ROC-AUC（Figure 2, 4）：

ChatGPT 攻击时，AUC 基本都从 KGW+23 的 0.88--0.95 提升到 0.95--0.99；
DIPPER 和 BART 攻击下，Unigram 的 AUC 也持续高出一截。

　　一句话总结：在各种 paraphrase 攻击下，Unigram-Watermark 明显更难被抹掉。

7.4 对编辑攻击的鲁棒性

论文 Figure 2(b)、Figure 4(b) -- 编辑攻击下的 ROC 曲线

　　作者还测试了三种简单但实用的编辑攻击：

Synonym replace-p：随机挑选 p 比例的 token，用同义词替换；
Delete-p：随机删除 p 比例的 token；
Swap-p：随机交换 p 比例的相邻 token。

　　p 取 0.1 / 0.3 / 0.5，覆盖从轻微编辑到"大改一半"的情况。

　　结果显示：

在 LFQA 和 OpenGen 上，Unigram 的 AUC 一直显著高于 KGW+23；
当 p 提升到 0.5 时，KGW+23 的 AUC 已经跌到 0.7 左右，而 Unigram 通常还能维持在 0.85--0.97 的区间。

　　这和理论定理完全吻合：只要攻击的编辑比例不接近 100%，z-score 的"优势"就不会被完全吃掉。

7.5 人类文本区分与偏见问题

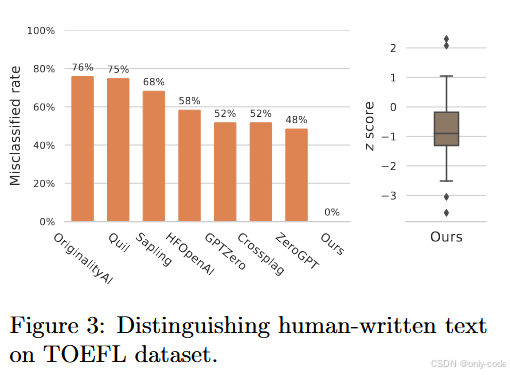
论文 Figure 3 -- TOEFL 数据集上的 z-score 分布

　　Liang et al. (2023) 提到：很多现有 AI 检测器会把非母语英语写作误判为 AI 生成。作者选用了同一份 TOEFL 作文数据集来测试：

他们对这些人类作文计算 z-score，发现绝大多数远低于经验阈值 6；
与此同时，若在同样的 prompt 下生成水印文本，z-score 则远高于 6。

　　和市面上一些通用检测器相比（OriginalityAI、GPTZero 等），Unigram 的"误判率"几乎可以视为 0。这说明这种基于水印的检测更像是"验证来源"，而不是"测文本像不像人写的"，因此天然减轻了对群体的偏见。

7.6 其他实验：参数敏感性、解码策略、放大模型

　　在附录中，作者还做了很多"工程向"的实验：

不同水印参数 δ, γ

　　- 增大 δ 会提升检测 TPR，但 perplexity 略升；

　　- 减小 γ（green list 更稀）也增强检测能力；

　　- 总体来看，(=2,=0.25--0.5) 是比较好的折衷。
不同解码策略

　　- 除了 nucleus sampling，还试了 multinomial sampling 和 beam search；

　　- 结果显示：各种策略下水印仍可有效检测；

　　- beam search 虽然 perplexity 更低，但会生成短而重复的句子，不太像真实使用场景。
放大到 LLaMA-13B / 65B

　　- 在 OpenGen 和 LFQA 上，TPR 在 1% FPR 下仍能保持在 0.78--1.0 的高位；

　　- 说明 Unigram-Watermark 对更大模型同样适用。
Alternative detector "Unique"

　　- 作者还提出了一个基于去重 token 的"Unique" 检测器，对某些攻击有更好表现；
- 但核心结论仍然是：Unigram 的水印信号足够强，可以多种方式读出来。

8. 亮点与创新点总结

　　如果只记住几个亮点，我会选这几个：

　　第一，极简而有效的设计。

　　整个 Unigram-Watermark 只做了一件事：把词表随机切一刀，然后对一半词统一加一个 logit 偏置。没有复杂的编码结构，不需要访问模型内部参数，更不需要改模型架构，本质是一个"解码层的小 hack"。

　　第二，把文本水印搬进了"可证明"世界。

　　作者不是只看图好看就说自己鲁棒，而是：

　　- 用 Rényi 散度 + 差分隐私工具证明了 水印对生成分布的上界影响 ；

用 concentration 不等式和高熵 / 同质性假设证明了 误报、漏报随长度指数下降 ；
把编辑攻击的影响写成 explicit 的 (\eta/\sqrt{n}) 上界，给出 "要改多少 token 才能藏住水印" 的定量结论。

　　第三，针对真实攻击场景的系统实证。

　　实验里用到的攻击对象包括 ChatGPT、DIPPER、BART 等现代 paraphraser，以及多种随机编辑操作，覆盖面非常现实；几乎所有实验中 Unigram 都比 KGW+23 更扛打，且质量不降。

　　第四，范式意义：从"检测是不是 AI"到"检测是不是这个模型"。

　　传统检测器试图做的是"AI vs 人"的分类，容易和写作水平、语言风格纠缠在一起；

　　而这种水印型方法做的是"是不是我家模型写的"，更像是"签名 / 指纹"，天然就有更清晰的使用边界，也更好解释。

　　第五，可扩展性与后续工作空间。

　　作者在结尾提到：

　　- 可以推广到 K≥2 的 K-gram 水印；

　　- 可以研究"不可学习水印"（unlearnable watermark），进一步增强攻击难度；

　　- 还可以尝试把统计水印与密码学水印统一起来，结合各自优势。

9. 局限性与不足

　　当然，这篇工作也不是"万能银弹"，作者自己在结论中也比较坦诚地写了几点限制，我们可以稍微再挖深一点：

依赖固定的 green/red 划分

　　- 固定划分带来的好处是鲁棒，但也意味着一旦攻击者掌握了相当数量的水印文本，就可能通过统计手段对 green list 做一定程度的推断；

　　- 虽然附录实验表明这种推断并不容易，但在极端强对手、长期交互场景下，这仍然是一个潜在风险。
理论假设未必总是满足

　　- 高熵假设和 homophily 假设在大多数 free-form 生成里是合理的，但在某些结构化任务（比如严格按模板输出、重复词很多的场景）里就不再成立；

　　- 在这些场景，水印的检测margin会收窄，Type II 错误可能上升。
编辑距离不等于"语义代价"

　　- 定理里使用的是 token 级编辑距离作为攻击成本度量；

　 - 但如果攻击者只关心"保留语义、不太在乎措辞变化"，那 paraphrase 模型完全可能进行大量编辑却保持读者感受相近；
- 虽然实验表明 paraphrase 攻击目前仍难以完全抹除 Unigram 的水印，但从理论角度看，edit distance 只是一个近似 proxy。
对生态的依赖

　　- 这种水印只有在"模型提供方愿意部署，并且检测方有密钥"的前提下才有用；

　　- 对于开源模型、第三方微调模型，或压根不用水印的服务，这一方案无法覆盖。
不可避免的 trade-off

　　- 想要更强水印（更大的 δ、更小的 γ），就要付出一些质量代价；

　　- 在应用层面，如何选择具体参数，使"检测力"和"体验"平衡，是一个需要产品化思考的问题。

10. 全文总结

　　回顾整篇论文，它做的事情其实很清晰：从"我要给 LLM 文本打上水印"这个需求出发，搭建了一套完整的理论框架，把生成质量、误报、漏报、抗编辑攻击都变成可以写成定理和上界的数学对象；然后在这个框架下，选择了最简单的 K=1 版本 K-gram 水印------Unigram-Watermark------并证明它在上述各个维度都表现良好。

　　方法上，它只是在解码时对一半词表统一加了一个 logit 偏置，用 z-score 检测 green token 的超额出现率，却在 DP 风格分析和集中不等式的支持下，保证了：水印不会明显破坏模型分布，却能让"自家模型生成的文本"和"非水印文本"在统计上逐渐拉开一条随 (\sqrt{n}) 增长的鸿沟。

　　实验上，从 GPT2-XL、OPT 到 LLaMA-7B，再到更大的 LLaMA-13B/65B，从 Wiki continuation 到 Reddit 长问答，从 paraphrase 到随机编辑，从人类作文到非母语写作，它几乎在所有场景下都展示出：检测能力强、对攻击鲁棒、对质量影响可忽略。

　　如果要用几句话浓缩这篇论文带来的观念变化，我会这样说：

检测 AI 文本，不必总是做"AI vs 人"的分类，我们可以让模型自己"签名"。
简单的统计水印，只要设计得当，也可以拥有相当硬核的理论保证。
鲁棒水印的关键，不只是"埋得多深"，更是在攻击和编辑的空间里，维持足够大的统计 margin。

　　如果你只看这一节，那么记住：Unigram-Watermark 是一个极简但可证明鲁棒的 LLM 文本水印方案，它通过固定 green/red 划分与 logits 偏置，在几乎不损伤文本质量的前提下，让"是不是这个模型生成的"这件事，有了一个既实用又可推理的答案。