图论专题(五)：图遍历的“终极考验”——深度「克隆图」

哈喽各位，我是前端小L。

欢迎来到我们的图论专题第五篇！我们已经学会了如何用 DFS 和 BFS 在图上"探险"，无论是找路径、开房间，还是枚举所有可能。那些都是"只读"操作。

今天，我们要进行"写 "操作。我们要扮演"造物主"，原模原样地复制一个图。这个图可能有环、有复杂的连接，我们的复制品必须和原作的结构一模一样。这道题，是检验我们是否真正理解了"遍历"与"递归"本质的试金石。

力扣 133. 克隆图

https://leetcode.cn/problems/clone-graph/

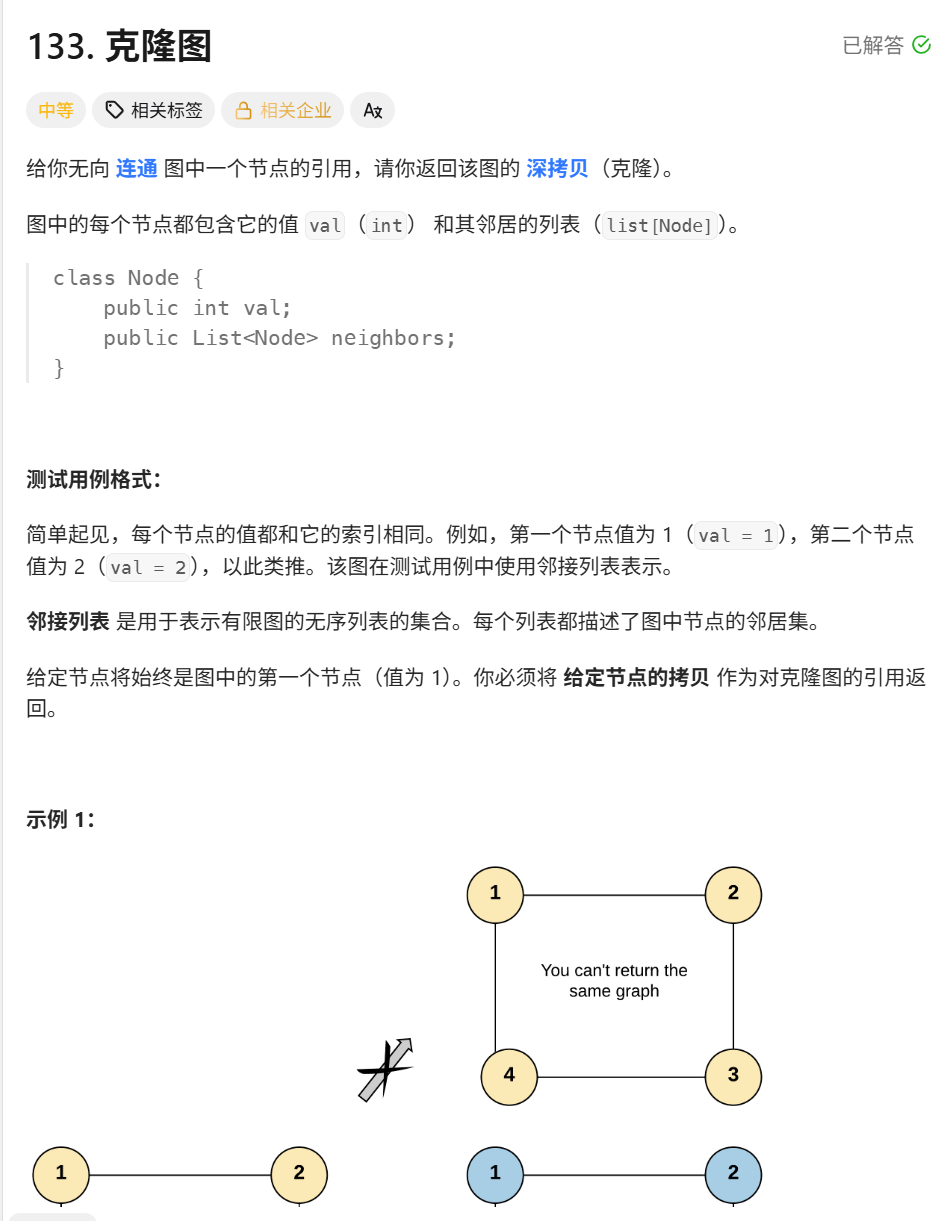
题目分析：

输入：一个无向连通图的某个节点 node。
节点定义 ：val (值), neighbors (一个 Node* 列表)。
目标：返回这个节点对应的克隆节点。
核心：这是一个深度克隆 (Deep Copy) 。你必须创建全新的 Node，并且新节点的 neighbors 列表，也必须指向新的克隆节点，而不是指向旧的原始节点。

"Aha!"时刻：最大的"陷阱"------环 最朴素的想法：写一个递归函数 clone(oldNode)。

创建一个 newNode，newNode->val = oldNode->val。
遍历 oldNode->neighbors 里的每个 neighbor。
newNode->neighbors.push_back(clone(neighbor))。
返回 newNode。

这会发生什么？假设 A 和 B 相互连接 ( A <-> B )。

clone(A) 被调用。
newA 被创建。
A 遍历邻居，找到 B。
调用 clone(B)。
newB 被创建。
B 遍历邻居，找到 A。
调用 clone(A) https://www.google.com/search?q=...
灾难发生！ 我们又在尝试创建 A，这将导致无限递归 和栈溢出。

解决方案：`visited` 数组的"终极进化"------哈希表

为了防止"兜圈"，我们需要一个 visited 数组。但一个 vector<bool> 够吗？不够！我们不仅需要知道"这个旧节点我是否见过了？ "，我们还需要知道"如果见过了，它对应的那个'克隆体'在哪里？"

这，正是哈希表 (HashMap / unordered_map) 的完美应用场景！

我们将创建一个哈希表： unordered_map<Node*, Node*> visited_and_cloned;

Key : Node* (原始图中的节点指针)
Value : Node* (我们为它创建的克隆节点指针)

这个哈希表，同时扮演了两个角色：

visited 集合 ：if (map.count(oldNode)) 就能判断是否访问过。
"克隆"注册表 ：map[oldNode] 能立刻返回我们之前创建的克隆体。

算法流程：DFS + 哈希表

创建一个全局（或通过引用传递）的哈希表 visited_map。
调用 dfs_clone(node)。
dfs_clone(oldNode) 函数的逻辑： a. Base Case : if (oldNode == nullptr) return nullptr; b. "查表" (防止循环) : if (visited_map.count(oldNode))，说明这个节点已经被克隆过了 ，我们必须返回它已有的克隆体：return visited_map[oldNode]; c. "克隆" (创建新节点) : Node* newNode = new Node(oldNode->val); d. "注册" (关键一步!) : 立刻将新旧节点配对，放入哈希表：visited_map[oldNode] = newNode; (必须在递归调用邻居之前注册，以防止在深层递归中（如 A->B->A），B 回访 A 时，A 还没被注册) e. "递归邻居" : 遍历 oldNode->neighbors 里的每个 oldNeighbor： i. Node* newNeighbor = dfs_clone(oldNeighbor); ii. newNode->neighbors.push_back(newNeighbor); f. 返回：return newNode;

代码实现 (DFS)

C++

复制代码

#include <vector>
#include <unordered_map>
#include <queue> // 仅用于 BFS 解法

using namespace std;

/*
// Definition for a Node.
class Node {
public:
    int val;
    vector<Node*> neighbors;
    Node() {
        val = 0;
        neighbors = vector<Node*>();
    }
    Node(int _val) {
        val = _val;
        neighbors = vector<Node*>();
    }
    Node(int _val, vector<Node*> _neighbors) {
        val = _val;
        neighbors = _neighbors;
    }
};
*/

class Solution {
private:
    // "灵魂"哈希表：<原始节点, 克隆节点>
    unordered_map<Node*, Node*> visited_and_cloned;

    Node* dfs_clone(Node* oldNode) {
        // 1. Base Case
        if (oldNode == nullptr) {
            return nullptr;
        }

        // 2. "查表" (防止循环)
        if (visited_and_cloned.count(oldNode)) {
            return visited_and_cloned[oldNode];
        }

        // 3. "克隆"
        Node* newNode = new Node(oldNode->val);
        
        // 4. "注册" (在递归邻居前)
        visited_and_cloned[oldNode] = newNode;

        // 5. "递归邻居"
        for (Node* oldNeighbor : oldNode->neighbors) {
            newNode->neighbors.push_back(dfs_clone(oldNeighbor));
        }

        // 6. 返回
        return newNode;
    }

public:
    Node* cloneGraph(Node* node) {
        // 清空哈希表，以防多组测试用例
        visited_and_cloned.clear();
        return dfs_clone(node);
    }
};

/*
// --- BFS 解法 (供参考) ---
class Solution_BFS {
public:
    Node* cloneGraph(Node* node) {
        if (!node) return nullptr;

        unordered_map<Node*, Node*> visited_map;
        queue<Node*> q;

        // 1. 克隆并注册起点
        Node* cloneRoot = new Node(node->val);
        visited_map[node] = cloneRoot;
        q.push(node);

        while (!q.empty()) {
            Node* currOld = q.front();
            q.pop();

            // 2. 遍历邻居
            for (Node* oldNeighbor : currOld->neighbors) {
                // 3. 如果邻居没被克隆过
                if (!visited_map.count(oldNeighbor)) {
                    Node* newNeighbor = new Node(oldNeighbor->val);
                    visited_map[oldNeighbor] = newNeighbor; // 注册
                    q.push(oldNeighbor); // 放入队列等待处理
                }
                
                // 4. 连接克隆节点
                // currOld 对应的克隆体是 visited_map[currOld]
                // oldNeighbor 对应的克隆体是 visited_map[oldNeighbor]
                visited_map[currOld]->neighbors.push_back(visited_map[oldNeighbor]);
            }
        }
        return cloneRoot;
    }
};
*/

深度复杂度分析

V (Vertices)：顶点数。
E (Edges)：边数。
时间复杂度 O(V + E)：
- 建图：无需建图。
- 遍历 (DFS/BFS) ：我们访问每个节点（V）有且仅有一次 （哈希表的保护）。在访问每个节点 u 时，我们会遍历它的所有邻居（u 的"度" deg(u)），这相当于遍历了它的所有"出边"。
- 整个遍历过程，我们访问了所有 V 个顶点，并遍历了所有 E 条边（在无向图中，每条边被遍历两次，2E）。
- 总时间 O(V + 2E) = O(V + E)。
空间复杂度 O(V)：
- visited_map 哈希表 ：需要存储 V 个键值对（V 个节点）。空间 O(V)。
- 辅助空间：
  - DFS 需要 O(H) 的递归栈 空间，H 是图的最大深度。最坏情况（一条长链）H=V。
  - BFS 需要 O(W) 的队列空间，W 是图的最大宽度。最坏情况（一个"星型图"）W=V-1。
- 总空间 = O(V) (哈希表) + O(V) (递归栈/队列) = O(V)。

总结

今天，我们用"克隆图"这道题，将"图遍历"的理解，提升到了"状态管理 "的层面。我们明白了，visited 不仅仅是一个 bool，它可以是一个哈希表 ，用来存储我们"已经处理过的子问题的答案"。

这，其实已经触及到了"记忆化搜索" (Memoization) 的本质，也是动态规划思想在图论中的一种完美体现。

在下一篇中，我们将把今天学到的 DFS/BFS，应用到最常见的"隐式图"------二维网格（"岛屿问题"）上！

下期见！