

🔥@晨非辰Tong: 个人主页
👀专栏:《C语言》、《数据结构与算法入门指南》
💪学习阶段:C语言、数据结构与算法初学者
⏳"人理解迭代,神理解递归。"
文章目录
- 引言:
- 一、排序算法背景摸底:归并排序是什么"人物"?
- 二、递归实现:自顶向下的分治艺术
-
- [2.1 算法框架:分解 → 解决 → 合并](#2.1 算法框架:分解 → 解决 → 合并)
- [2.2 归并操作核心组成:"分治法"的"来世今生"](#2.2 归并操作核心组成:“分治法”的“来世今生”)
-
- [2.2.1 算法思路解析:双指针与临时数组](#2.2.1 算法思路解析:双指针与临时数组)
- [2.2.2 代码实战:完整实现](#2.2.2 代码实战:完整实现)
- [2.2.3 **==代码分析:递归终止与指针移动==**](#2.2.3 ==代码分析:递归终止与指针移动==)
- 三、非递归实现:自底向上的迭代方案
-
- [3.1 算法思路深度解析:步长倍增与两两合并](#3.1 算法思路深度解析:步长倍增与两两合并)
- [3.2 代码实战:完整迭代实现](#3.2 代码实战:完整迭代实现)
- [3.3 **==代码分析:细节的边界处理==**](#3.3 ==代码分析:细节的边界处理==)
- 四、算法对比:递归vs非递归的性能分析
- 总结
引言:
归并排序是一种基于"分治"思想的高效排序算法,核心思路 是将数组
不断拆分再有序合并,保证稳定在O(n log n)时间复杂度。本文将对比解析其两种实现:直观的递归分治与高效的非递归迭代,通过图解、代码与性能分析,帮你彻底掌握这一经典算法。
一、排序算法背景摸底:归并排序是什么"人物"?
归并排序(MERGE-SORT)是建立在归并操作上的⼀种有效的排序算法,是采用分治法(Divide and Conquer)的⼀个非常典型的应用。
算法思想:将已有序的子序列合并,得到完全有序的序列;即先使每个子序列有序,再使子序列段间有序。若将两个有序序列合并成一个有序序列,称为二路归并。
二、递归实现:自顶向下的分治艺术
2.1 算法框架:分解 → 解决 → 合并
c
//归并排序
void MergeSort(int* arr, int n)
{
int* tmp = (int*)malloc(sizeof(int) * n);
//[0,n-1]
_MergeSort(arr, 0, n - 1, tmp);
free(tmp);
}2.2 归并操作核心组成:"分治法"的"来世今生"
"分治法"在应用时采用了"二分序列"的方法,但不是绝对的"二分序列"。归并排序的分治操作,通常是通过不断地二分序列,直到子序列有序,然后再合并。
首先分治是一种思想,分治本身并没有规定一定要"二分"。
- 分:将一个大问题分解成若干个规模较小的子问题。
- 治:递归地解决这些子问题。
- 合:将子问题的解合并起来,得到原问题的解。
2.2.1 算法思路解析:双指针与临时数组
- 作图分析
- 具体分析
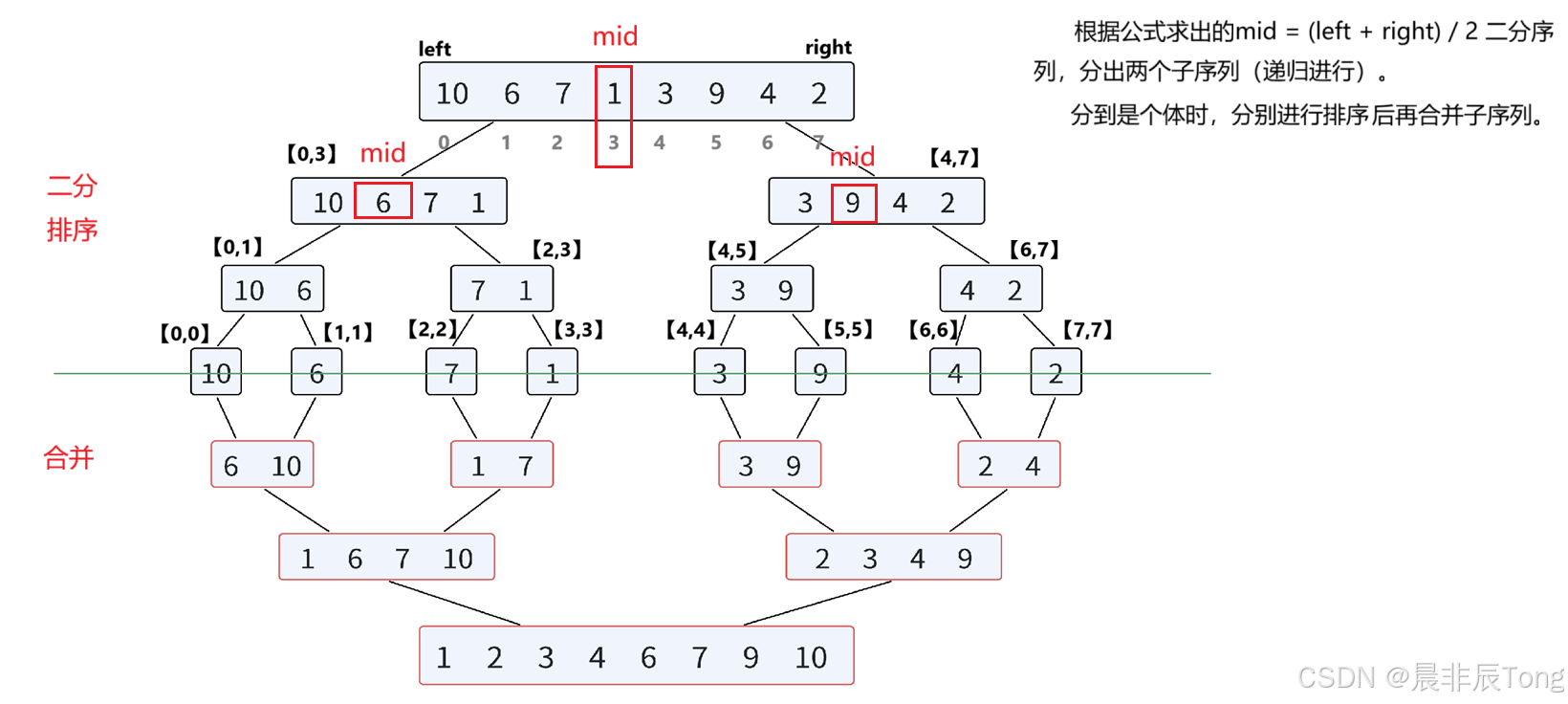
"二分 ":首先定义变量left、right明确序列的边界,也为了后面区分子序列做准备。然后就要确定序列的中间值mid = (left+right) / 2,根据下标得出左子序列为[left,mid],右子序列为[mid+,right1](当然left,right需要再次定义变量进行接收,防止原序列边界变化,方便为了后面的合并操作)。
"二分表现 ":原序列------> [10, 6, 7, 1, 3, 9, 4, 2],经过一次"分" ------> [10, 6, 7, 1]、[3, 9, 4, 2],就这样递归进行,最后"分"成个体 ------>[10],[6],[7],[1],[3],[9],[4],[2],再对应分组两两排序对比。
"合并":经过"二分"部分后,将有序的及逆行合并,相当于合并两个有序序列的操作,最终完成排序。
2.2.2 代码实战:完整实现
--大家自行将代码分成多个文件。
c
//"分治法"实现
void _MergeSort(int* arr, int left, int right, int* temp)
{
//当二分到个体时直接返回
if (left >= right)
{
return;
}
//中间值,分为两个子序列
int mid = (left + right) / 2;
//递归分解
_MergeSort(arr, left, mid, temp);//左
_MergeSort(arr, mid + 1, right, temp);//右
//开始分别排序、合并
//防止边界变化,新定义子序列边界
int begin1 = left, end1 = mid;
int begin2 = mid + 1, end2 = right;
int index = left;//下标
//循环遍历比较--从个体开始
while (begin1 <= end1 && begin2 <= end2)
{
if (arr[begin1] < arr[begin2])
{
temp[index++] = arr[begin1++];
}
else
{
temp[index++] = arr[begin2++];
}
}
//将子序列剩余的数组循环放入
//序列1剩余
while(begin1 <= end1)
{
temp[index++] = arr[begin1++];
}
//序列2剩余
while (begin2 <= end2)
{
temp[index++] = arr[begin2++];
}
//拷贝到原数组
for (int i = left; i <= right; i++)
{
arr[i] = temp[i];
}
}
//归并排序
void MergeSort(int* arr, int n)
{
int* tmp = (int*)malloc(sizeof(int) * n);
//[0,n-1]
_MergeSort(arr, 0, n - 1, tmp);
free(tmp);
}
test01()
{
//int arr[] = {6, 2, 7, 3};
int arr[] = { 5,3,9,6,2,4, 7, 1, 8 };
int n = sizeof(arr) / sizeof(arr[0]);
printf("排序之前:");
PrintArr(arr, n);
QuickSort(arr, 0, n - 1);
//归并排序-递归
MergeSort(arr, n);
printf("排序之后:");
PrintArr(arr, n);
}
int main()
{
test01();
return 0;
}
2.2.3 代码分析:递归终止与指针移动
-
关于下标的定义
int index = left;为什么不是从0开始?因为这是在递归调用函数内部用到,每个序列的起点不同。等于0就会导致重复覆盖前一段的序列内容。
-
为什么会有循环将序列剩余元素放入数组?
因为是两个比较后将小的放入,当有一个序列的比较完了但是另一个剩余很多(本身是有序的)就需要额外的循环来放入。
三、非递归实现:自底向上的迭代方案
3.1 算法思路深度解析:步长倍增与两两合并
-
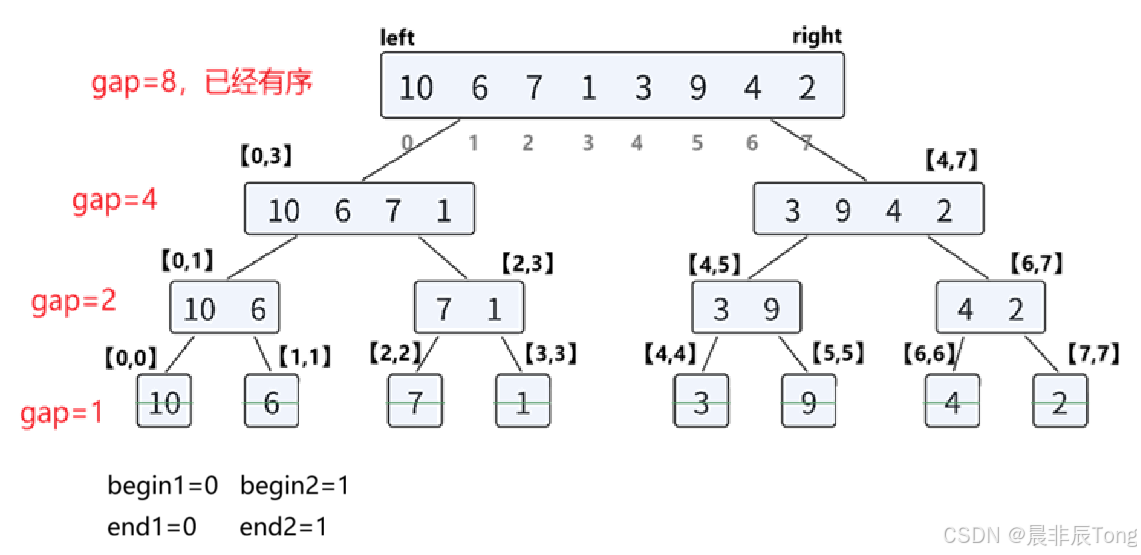
初始化
gap从最小的子数组开始,即步长
gap = 1。意味着最初将每个单独的元素视为一个已排序的长度为1的子序列。 -
两两合并
从左到右遍历数组,将相邻的两个子序列(序列1、序列2)合并成一个更大的有序序列。
第一次循环 (gap=1):合并 [10] 和 [6],[7] 和 [1],[3] 和 [9]...
第二次循环 (gap=2):合并 [10,6] 和 [7,1]...
第三次循环 (gap=4):...
-
处理边界情况
在合并时,可能会遇到三种情况:
情况一: 完整的两个子序列(两个序列成功配对)。
情况二: 只剩下一个子序列(只有序列1,序列2不存在)。这个子序列已经有序,无需合并。
情况三: 序列末尾剩下的元素数量不足以构成一个完整的序列2,改变右边界,进行合并。
-
gap增加每一轮合并完成后,将
gap乘以 2 (gap *= 2)。这表示下一轮要合并的子序列大小是当前的两倍。 -
循环终止
当步长大于或等于整个数组的长度 n 时,说明整个数组已经被合并成一个完整的有序数组,排序完成。
3.2 代码实战:完整迭代实现
c
//非递归版--归并排序
void MergeSortNore(int* arr, int n)
{
//开辟临时数组
int* temp = (int*)malloc(sizeof(int) * n);
if (temp == NULL)
{
perror("malloc fail!");
exit(1);
}
//从个体开始
int gap = 1;//代表一组就一个数据
//根据gap开始分组
while (gap < n)
{
//分组,两两比较合并
for (int i = 0;i < n; i += 2*gap)//注意条件的设置
{
//子序列1
int begin1 = i, end1 = i + gap - 1;
//子序列2
int begin2 = i + gap, end2 = i + 2 * gap - 1;
//特殊情况--没配对
if (begin2 >= n)//序列2没有
{
break;
}
if (end2 >= n)//单个
{
end2 = n - 1;
}
//两个序列进行比较合并
int index = begin1;
while (begin1 <= end1 && begin2 <= end2)
{
if (arr[begin1] < arr[begin2])
{
temp[index++] = arr[begin1++];
}
else
{
temp[index++] = arr[begin2++];
}
}
//将某序列剩余元素合并
while (begin1 <= end1)
{
temp[index++] = arr[begin1++];
}
while (begin2 <= end2)
{
temp[index++] = arr[begin2++];
}
//导入到原数组
memcpy(arr + i, temp + i, sizeof(int) * (end2 - i + 1));
}
gap *= 2;//向上合并
}
free(temp);
}
//打印
void PrintArr(int* arr, int n)
{
for (int i = 0; i < n; i++)
{
printf("%d ", arr[i]);
}
printf("\n");
}
test01()
{
//int arr[] = {6, 2, 7, 3};
int arr[] = { 5,3,9,6,2,4, 7, 1, 8 };
int n = sizeof(arr) / sizeof(arr[0]);
printf("排序之前:");
PrintArr(arr, n);
//非递归--归并
MergeSortNore(arr, n);
printf("排序之后:");
PrintArr(arr, n);
}
int main()
{
test01();
return 0;
}
3.3 代码分析:细节的边界处理
-
对于循环的比较合并
for (int i = 0;i < n; i += 2*gap),i的设置?
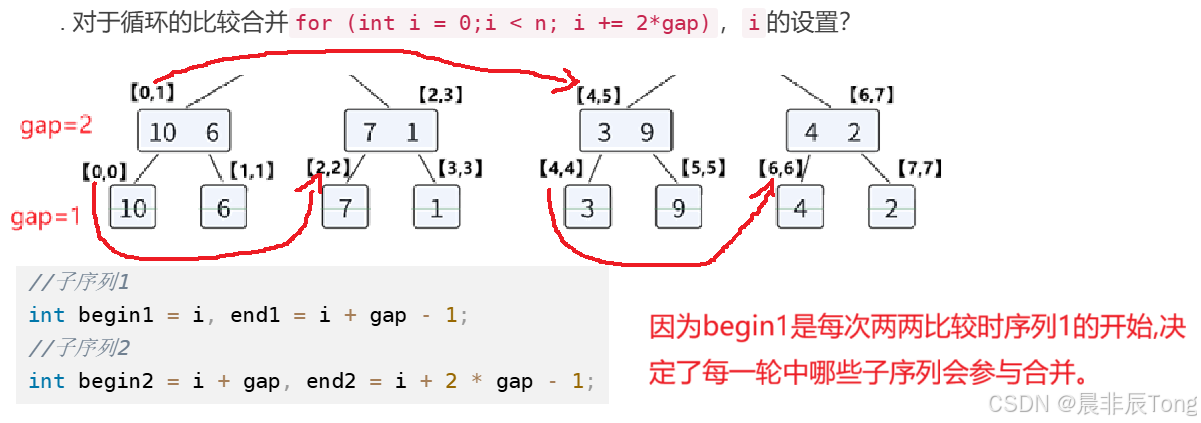
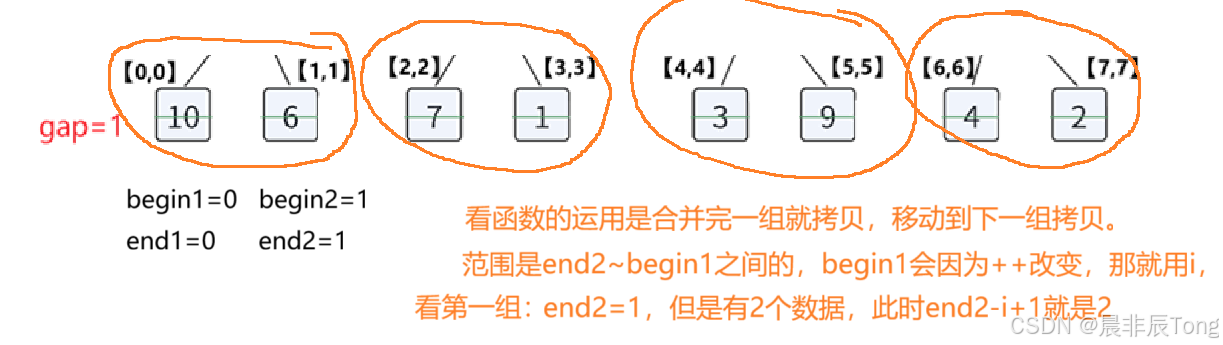
观察图示:两两比较合并,由于步长
gap的增加,每一个序列的大小也在变化,所以begin1下标的跳转**(看红色箭头指向)**要根据步长调整。 -
特殊情况的处理条件:
begin2 >= n、end2 >= n目的是什么?这就是前面算法解析的边界处理情况2、3;
对于
begin2 >= n,判断没有序列2,直接进行下一轮gap;对于
end2 >= n,在当前gap下不能构成一个完整序列2,但是改变右边界,仍进行比较合并。
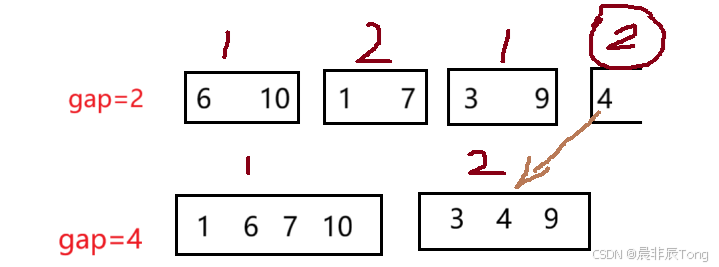
-
拷贝函数
end2 - i + 1设置原因?核心就是
end2~begin1之间的数据是要进行拷贝的。看图示:
四、算法对比:递归vs非递归的性能分析
| 特性维度 | 递归版归并排序 | 递归版归并排序 |
|---|---|---|
| 实现方式 | 自顶向下递归分解数组 | 自底向上循环迭代合并 |
| 算法思路 | 递归将数组二分,直到单个元素逐层,合并返回 | 从单个元素开始,按gap倍增,合并直到整个数组有序 |
| 时间复杂度 | 稳定 O(n log n) | 稳定 O(n log n) |
选择建议
- 学习理解:推荐递归版,概念更清晰;
- 生产环境:推荐非递归版,性能更稳定;
- 内存限制:非递归版更适合内存敏感场景;
- 代码维护:递归版更易于阅读和修改。
总结
html
🍓 我是晨非辰Tong!若这篇技术干货帮你打通了学习中的卡点:
👀 【关注】跟我一起深耕技术领域,从基础到进阶,见证每一次成长
❤️ 【点赞】让优质内容被更多人看见,让知识传递更有力量
⭐ 【收藏】把核心知识点、实战技巧存好,需要时直接查、随时用
💬 【评论】分享你的经验或疑问(比如曾踩过的技术坑?),一起交流避坑
🗳️ 【投票】用你的选择助力社区内容方向,告诉大家哪个技术点最该重点拆解
技术之路难免有困惑,但同行的人会让前进更有方向~愿我们都能在自己专注的领域里,一步步靠近心中的技术目标!结语:归并排序是分治算法的经典实现,通过递归分解或迭代合并达到稳定高效的排序效果。其核心在于掌握递归的时间复杂度分析和迭代的空间优化,理解分治思想中"分解-解决-合并"的完整流程。该算法不仅提供了可靠的排序方案,更体现了算法设计中时间与空间的本质权衡,是深入学习算法设计与分析的典范案例。