9.12 sinc插值 - 技术栈

文章目录

公式
例子
实验

公式

前文讲了傅里叶变换家族，如果要讲清楚，得单开一个专栏，这里就拿其中的sinc插值作为本专栏完结文章。

Sinc变换，大白话就是将离散的的采样点，完美还原为函数。其公式超级简单：
x ( t ) = ∑ n = − ∞ ∞ x [ n ] ⋅ sinc ⁡ ( t − n T T ) x(t) = \sum_{n=-\infty}^{\infty} x[n] \cdot \operatorname{sinc}\left( \frac{t - nT}{T} \right) x(t)=n=−∞∑∞x[n]⋅sinc(Tt−nT)

其中sinc函数是归一化的定义：
sinc ⁡ ( x ) = { sin ⁡ ( π x ) π x if x ≠ 0 1 if x = 0 \operatorname{sinc}(x) = \begin{cases} \dfrac{\sin(\pi x)}{\pi x} & \text{if } x \neq 0 \\ 1 & \text{if } x = 0 \end{cases} sinc(x)=⎩ ⎨ ⎧πxsin(πx)1if x=0if x=0

T就是采样周期（不是数据展现的周期）， n n n就是采样点的编号。

例子

以下列数据为例子：

采样点编号	采样时间	数值
0	0.5	7
1	1	6
2	1.5	7
3	2	-1
4	2.5	7

周期 T = 0.5 T=0.5 T=0.5，代入公式就是：
x ( t ) = 7 sinc ⁡ ⁣ ( t − 0 2 ) + 6 sinc ⁡ ⁣ ( t − 0.5 2 ) + 7 sinc ⁡ ⁣ ( t − 1 2 ) − 1 sinc ⁡ ⁣ ( t − 1.5 2 ) + 7 sinc ⁡ ⁣ ( t − 2 2 ) \begin{aligned} x(t)=&\;7\;\operatorname{sinc}\!\Bigl(\frac{t-0}{2}\Bigr) +6\;\operatorname{sinc}\!\Bigl(\frac{t-0.5}{2}\Bigr) \\ &+7\;\operatorname{sinc}\!\Bigl(\frac{t-1}{2}\Bigr) -1\;\operatorname{sinc}\!\Bigl(\frac{t-1.5}{2}\Bigr) \\ &+7\;\operatorname{sinc}\!\Bigl(\frac{t-2}{2}\Bigr) \end{aligned} x(t)=7sinc(2t−0)+6sinc(2t−0.5)+7sinc(2t−1)−1sinc(2t−1.5)+7sinc(2t−2)

实验

将代码写好，再看看效果：

python 复制代码

import matplotlib
import numpy as np
import matplotlib.pyplot as plt

# -------------------------------------------------
# 1. 参数
T = 0.5                                 # 采样周期
                   # 采样点编号 0~4
x_n = np.array([7, 6, 7, -1, 7])       # 对应的幅值
n = np.arange(0, len(x_n))
# 2. sinc 插值函数（归一化 sinc）
def sinc_interp(t):
    """在任意实数 t 处返回 sinc 插值结果"""
    # 计算每个基函数的贡献并求和
    # np.sinc 的定义为 sin(pi*x)/(pi*x)，恰好是归一化 sinc
    # 这里的自变量是 (t - n*T)/T
    return np.sum(x_n[:, None] *
                  np.sinc((t[None, :] - n[:, None] * T) / T), axis=0)

if __name__ == "__main__":
    # 3. 生成绘图用的时间轴
    t_fine = np.linspace(0, 12, 2000)   # 细密采样，覆盖几个周期

    # 4. 计算插值曲线
    x_fine = sinc_interp(t_fine)
    matplotlib.rcParams['font.family'] = 'Microsoft YaHei'  # Windows 常用

    # 5. 绘图
    plt.figure(figsize=(8, 4))
    # 连续插值曲线
    plt.plot(t_fine, x_fine, label='Sinc 插值', color='steelblue')
    # 采样点（用实心圆标记）
    plt.scatter([i * T for i in n], x_n, color="steelblue", s=60, edgecolor="k", alpha=0.8)
    # 美化
    plt.title(f'Sinc 插值重建（周期 $T={T}$）')
    plt.xlabel('时间 $t$')
    plt.ylabel('幅值')
    plt.grid(True, which='both', ls='--', alpha=0.5)
    plt.legend()
    plt.tight_layout()
    plt.gca().set_aspect('equal', adjustable='box')
    plt.show()

效果为：

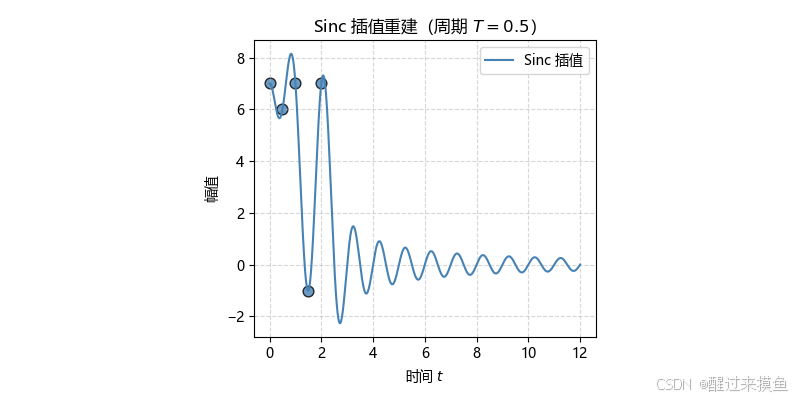
可见，并不能还原为周期函数，在采样范围外，是越来越离谱了。