在阅读本文前,建议读者优先阅读专栏内前面的文章。
目录
前言
本文主要介绍几道与链表相关的OJ题目的解法。
一、链表算法OJ题1:返回倒数第k个节点
我这里先把题目测试链接贴在下面:
面试题 02.02. 返回倒数第 k 个节点 - 力扣(LeetCode)
题目具体叙述如下:

思路一:
我们的思路是通过两次遍历链表来查找倒数第k个节点的值。首先遍历链表统计总长度len,然后计算出倒数第k个节点的正向位置为len - k,最后再次遍历链表,将指针移动到该位置,返回对应节点的值。该方法逻辑直接但需两次遍历,所以比较耗费时间,我给出代码示例:
cpp
typedef struct ListNode ListNode;
int kthToLast(struct ListNode* head, int k) {
ListNode* pcur = head;
int len = 0;
while(pcur != NULL){
len++;
pcur = pcur->next;
}
len -= k;
pcur = head;
while(len--){
pcur = pcur->next;
}
return pcur->val;
}
思路二:
当然我们也可以采用快慢指针法,通过一次遍历链表实现查找倒数第k个节点值的功能,核心利用快慢指针的距离差定位目标节点。具体思路为先初始化快慢指针均指向链表头节点,让快指针单独向前移动k步,此时快慢指针间形成k个节点的距离差;接着让快慢指针同时向后移动,当快指针指向空时,慢指针恰好走到链表倒数第k个节点的位置,最后返回慢指针所指节点的数值即可。请读者思考代码如何实现,我这里给出示例:
cpp
typedef struct ListNode ListNode;
int kthToLast(struct ListNode* head, int k) {
ListNode* fast = head;
ListNode* slow = head;
while(k--){
fast = fast->next;
}
while(fast != NULL){
fast = fast->next;
slow = slow->next;
}
return slow->val;
}
本题讲解结束。
二、链表算法OJ题2:链表的回文结构
我这里先把题目测试链接粘贴在下面:
题目详细叙述如下:
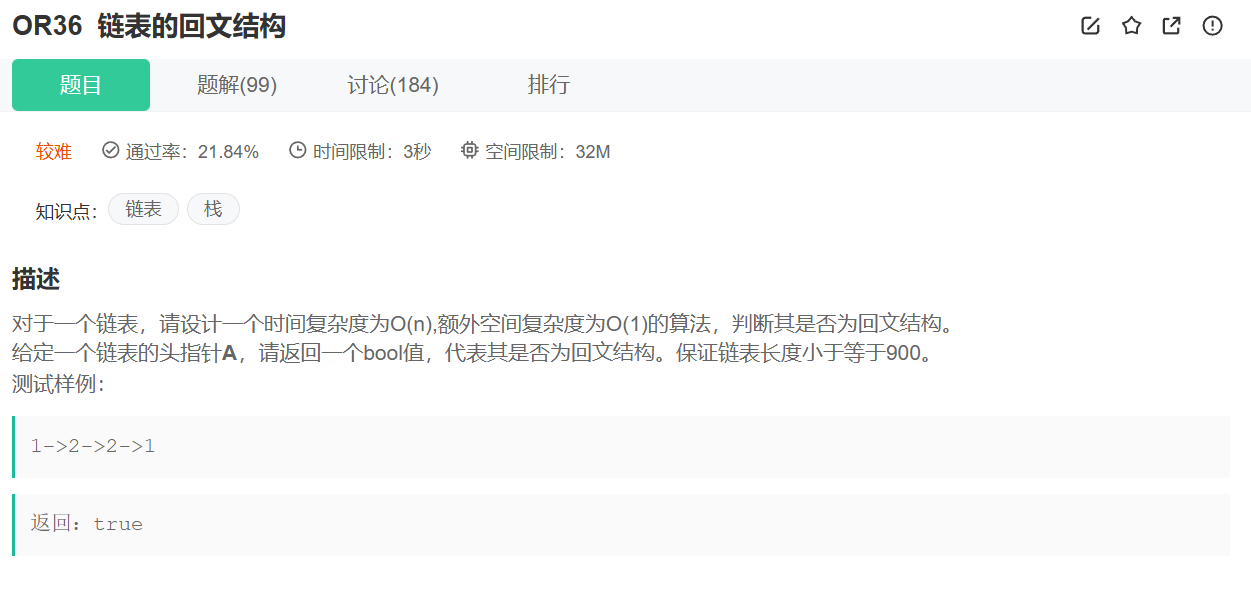
本道题具体可以参考我在刷题专栏中2025年11月19日的刷题记录,里面有详细的刷题记录,这里仅粘贴代码,不再赘述。
cpp
struct ListNode* reverseList(struct ListNode* head) {
struct ListNode* prev = NULL;
struct ListNode* curr = head;
while (curr != NULL) {
struct ListNode* nextTemp = curr->next;
curr->next = prev;
prev = curr;
curr = nextTemp;
}
return prev;
}
struct ListNode* endOfFirstHalf(struct ListNode* head) {
struct ListNode* fast = head;
struct ListNode* slow = head;
while (fast->next != NULL && fast->next->next != NULL) {
fast = fast->next->next;
slow = slow->next;
}
return slow;
}
bool isPalindrome(struct ListNode* head) {
if (head == NULL) {
return true;
}
// 找到前半部分链表的尾节点并反转后半部分链表
struct ListNode* firstHalfEnd = endOfFirstHalf(head);
struct ListNode* secondHalfStart = reverseList(firstHalfEnd->next);
// 判断是否回文
struct ListNode* p1 = head;
struct ListNode* p2 = secondHalfStart;
bool result = true;
while (result && p2 != NULL) {
if (p1->val != p2->val) {
result = false;
}
p1 = p1->next;
p2 = p2->next;
}
// 还原链表并返回结果
firstHalfEnd->next = reverseList(secondHalfStart);
return result;
}本题讲解到此结束。
三、链表算法OJ题3:相交链表
我这里先把题目测试链接粘贴在下面:
题目详细叙述如下:

我的核心思路是通过统计两个链表的长度差,补平遍历起点后同步移动指针,从而找到两个链表的相交节点。具体逻辑为首先初始化指针分别指向两个链表的头节点,遍历链表并统计各自的长度;计算两个链表的长度差,让指向较长链表的指针先向前移动长度差的步数,使两个指针后续遍历的剩余节点数一致;随后让两个指针同时向后移动,若遇到指向同一地址的节点,该节点即为相交节点并返回;若遍历至链表末尾仍未找到相同节点,则返回NULL表示两链表无相交。请读者思考代码如何实现,我这里给出我的代码:
cpp
typedef struct ListNode ListNode;
struct ListNode* getIntersectionNode(struct ListNode* headA,
struct ListNode* headB) {
int lenA = 1;
int lenB = 1;
ListNode* pA = headA;
ListNode* pB = headB;
while (pA != NULL) {
pA = pA->next;
lenA++;
}
while (pB != NULL) {
pB = pB->next;
lenB++;
}
pA = headA;
pB = headB;
int n = 0;
if (lenA >= lenB) {
n = lenA - lenB;
while (n--) {
pA = pA->next;
}
} else {
n = lenB - lenA;
while (n--) {
pB = pB->next;
}
}
while ((pA != NULL) && (pB != NULL)) {
if (pA == pB) {
return pA;
}
pA = pA->next;
pB = pB->next;
}
return NULL;
}
本题讲解到此结束。
四、链表算法OJ题4:环形链表
我先把题目测试链接粘贴在下面:
题目详细叙述如下:
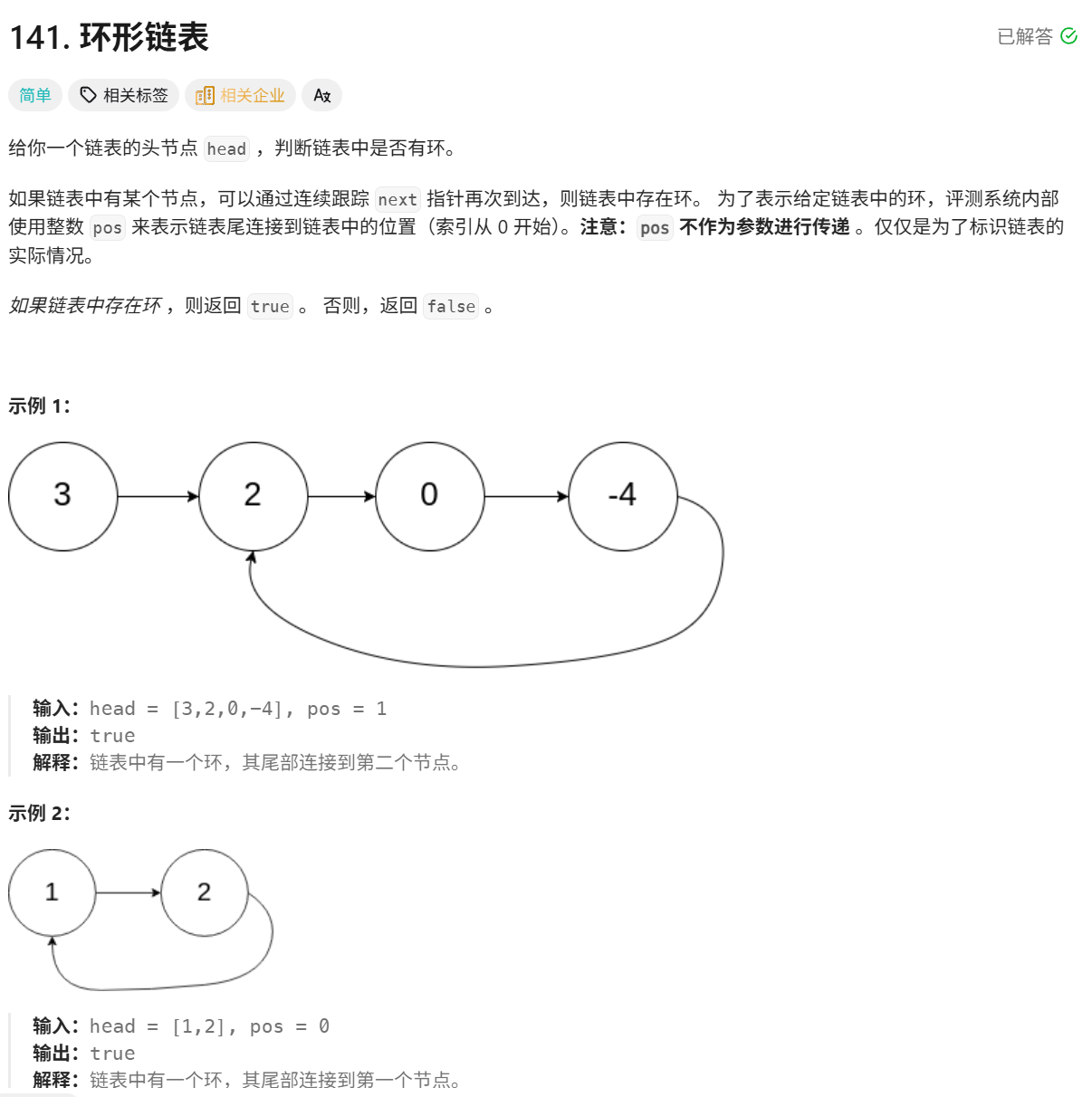
我的思路是采用快慢指针法检测链表是否存在环,核心利用快慢指针的速度差实现高效判断。具体思路为先判断链表为空或仅有一个节点的情况,直接返回无环;初始化快慢指针均指向头节点,慢指针每次向后移动1步,快指针每次向后移动2步;在快指针未指向空且其下一个节点也不为空的循环条件下持续移动,若快慢指针相遇,则说明链表存在环并返回true;若快指针先遍历到链表末尾则链表无环,返回false。请读者思考代码实现,我这里给出我的代码:
cpp
typedef struct ListNode ListNode;
bool hasCycle(struct ListNode *head) {
if((head == NULL) || (head->next == NULL)){
return false;
}
ListNode* fast = head;
ListNode* slow = head;
while((fast != NULL) && (fast->next != NULL)){
slow = slow->next;
fast = fast->next->next;
if(slow == fast){
return true;
}
}
return false;
}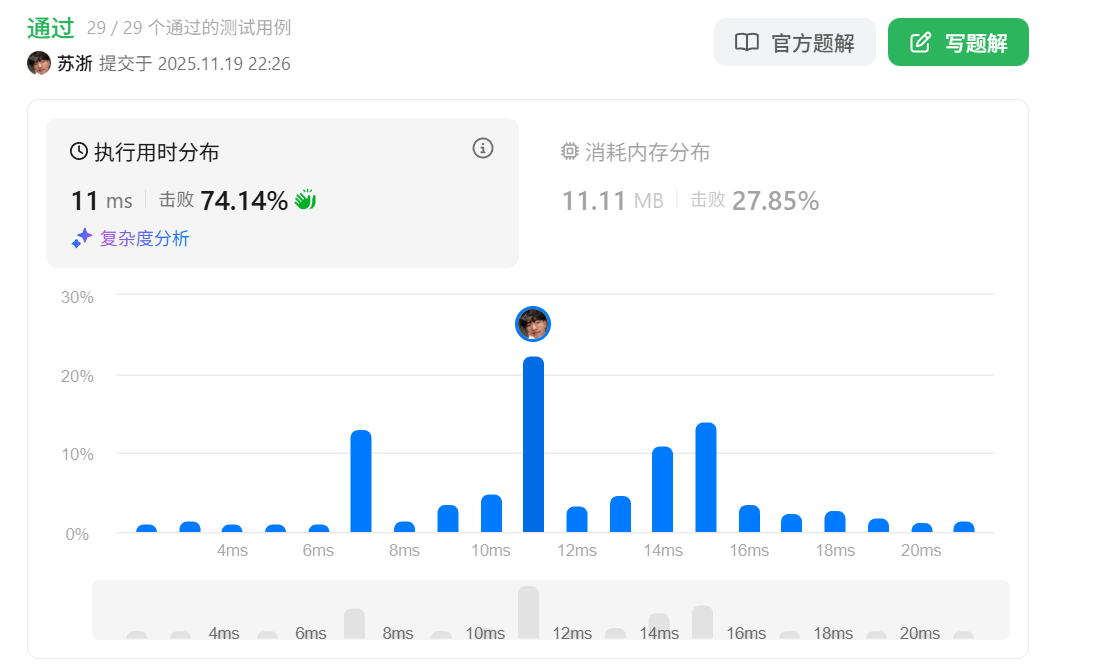
这个代码实现相对来说比较简单,我那么我们接下来来思考一下一些拓展的问题。首先我们来思考一下,为什么快慢指针一定会相遇,有没有可能二者会错过,永远都追不上,请证明结论。
我们首先假设链表存在环,若不存在环,快指针会率先走到链表末尾NULL,直接返回无环,不在本次证明范围内,慢指针每次向后移动1步;每次向后移动2步;设链表的非环部分长度为L(,环的长度为C;所有分析基于指针进入环后,在环内做循环移动的特性。当慢指针进入环时,快指针已在环内某位置,当慢指针走了L步时,会到达环的入口节点。此时快指针的移动步数是慢指针的 2倍,即走了2L步;快指针先走完非环部分的 L 步,进入环;剩余的2L - L = L步在环内移动,因此快指针在环内的位置为pos = L % C,即快指针在环内距离入口节点的偏移量为pos,%为取余运算。此时,快慢指针都处于环内,慢指针在环入口,快指针在环内偏移pos的位置,两者的环内相对距离为d,若pos = 0则快指针也在环入口,此时快慢指针直接相遇;若pos > 0则环形结构中,相对距离取最短路径,即d = C - pos,快指针在慢指针后方d步的位置,因为环是封闭的。
快慢指针的相对速度为1步/次,距离持续缩小,慢指针速度为1步/次,快指针速度为2步/次,因此快指针相对于慢指针的速度为1步/次。对于环内的初始相对距离d。每一次循环,快指针都会向慢指针靠近1步,两者的相对距离变为d-1;经过d次循环后,相对距离变为0,即快指针追上慢指针,两者相遇。
而为什么两者不会发生跳过呢,原因如下,若某一时刻,快慢指针的相对距离为1步,慢指针走1步,快指针走2步,则快指针刚好追上慢指针;若某一时刻,快慢指针的相对距离为2步:慢指针走 1步,快指针走2步,则下次循环就会追上;以此类推,由于相对速度是1步/次,快指针每次只会向慢指针靠近1步,不会出现 "跨步跳过" 的情况。也就是说,我们可以得出结论,在链表存在环的前提下,快慢指针的相对速度为1步/次,环内的相对距离会以1步/次的速度持续缩小,最终必然相遇。因此,用快慢指针检测链表环时,只要存在环,就一定能通过指针相遇判定,不会出现永远追不上的情况。
然后我们考虑一下,如果说快指针不是走两步,而是三步、四步甚至更多,是不是还会有与上面相似的结论?
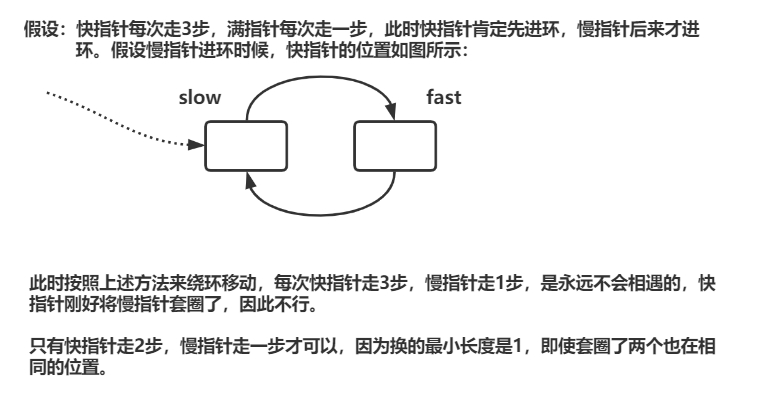
我们在上面的图片中简单讨论了一下情况,接下来我们尝试严密地证明一下。当快指针的步长超过 2步,如3步、4步甚至更多时,不再能保证快慢指针一定相遇,而是可能会出现永远错过、无限循环的情况。这一结论的核心在于快慢指针的相对速度与环的长度的最大公约数 ,决定了两者是否能相遇------只有当相对速度与环长的最大公约数能整除初始相对距离时,才会相遇;否则会陷入循环,永远错过。
假设链表存在环,定义慢指针每次移动1步;快指针每次移动k步;非环部分长度为L,环的长度为C;当慢指针走L步进入环入口时,快指针已走k*L步:先走完L步进入环,剩余(k*L - L) = L*(k-1)步在环内移动,因此快指针在环内的初始位置为 pos = [L*(k-1)] % C;快慢指针的初始相对距离为d,环形结构中,相对距离取快指针到慢指针的最短步数,即d = (C - pos) % C;快慢指针的相对速度为v = k - 1:快指针每次比慢指针多走k-1步。
快慢指针相遇的本质是存在正整数t,使得t次移动后,快指针通过相对速度弥补初始相对距离d,且总弥补的步数是环长C的整数倍。我们可以将上述关系转化为线性同余方程:
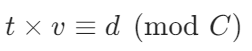
这个方程的含义是t次移动后,快指针相对慢指针走的步数t*v,减去初始相对距离d,结果是环长C的整数倍即绕环整数圈后追上。根据数论中线性同余方程解的存在性,我们必须要满足相对速度与环长的最大公约数能整除初始相对距离,否则方程会无解使整个过程陷入死循环。此时我们再看看上面这个图,就可以很好的理解了。
本题讲解到此为止。
五、链表算法OJ题5:环形链表的入环节点
我先把题目的链接粘贴在下面:
题目详细叙述如下:
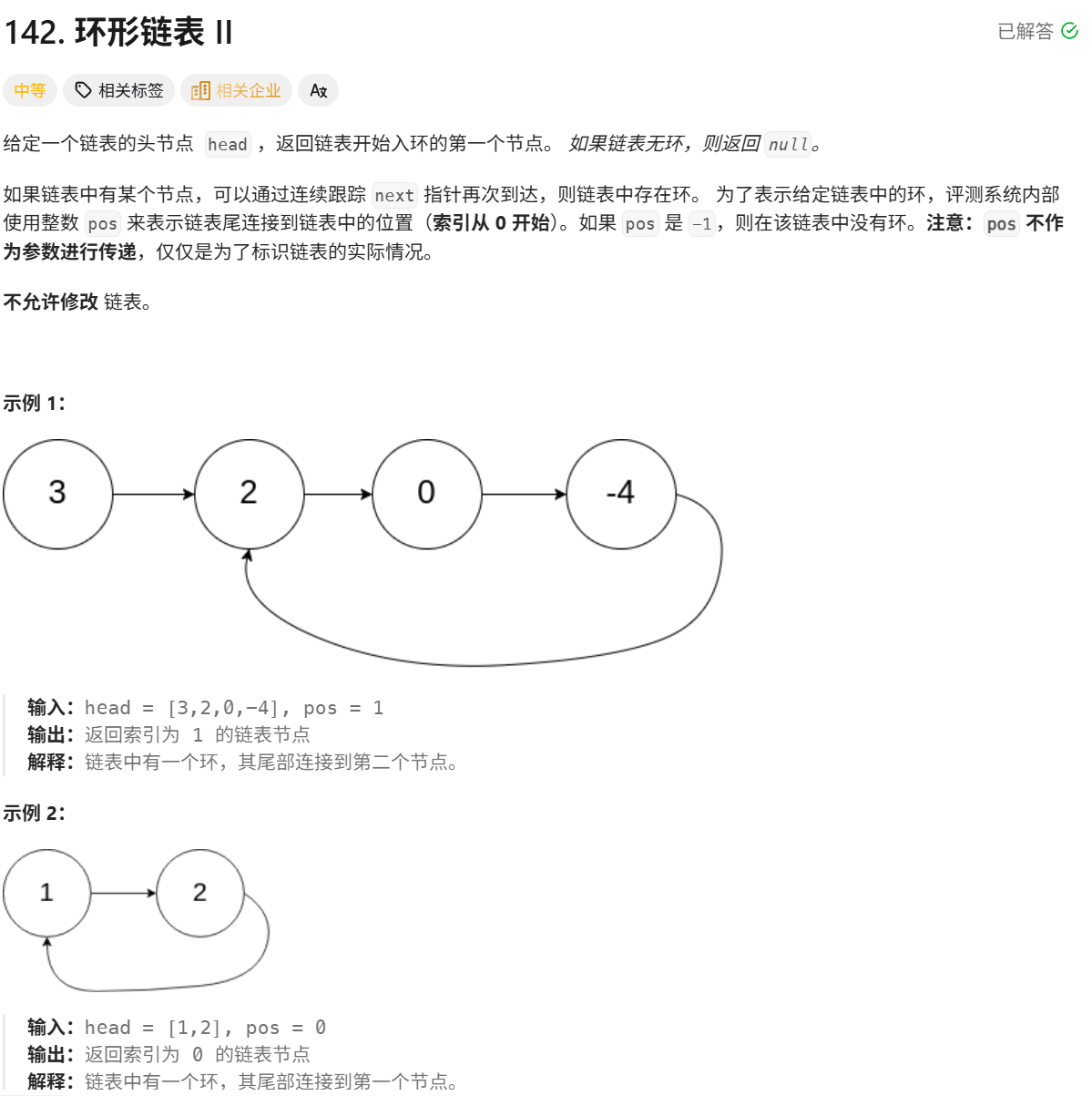
本题有一个极其简单的解法,就是采用快慢指针法分两阶段实现链表环入口节点的检测,第一阶段初始化快慢指针均指向头节点,快指针每次移动2步、慢指针每次移动1步,若指针相遇则说明链表存在环并跳出循环,若快指针走到链表末尾则返回NULL表示无环;第二阶段将慢指针重置为头节点,快慢指针以相同速度同步移动,当二者再次相遇时,该相遇节点即为环的入口节点,最终返回该节点。请读者思考代码如何实现,我这里给出示例代码:
cpp
typedef struct ListNode ListNode;
struct ListNode* detectCycle(struct ListNode* head) {
if (head == NULL) {
return NULL;
}
ListNode* fast = head;
ListNode* slow = head;
while (fast != NULL && fast->next != NULL) {
fast = fast->next->next;
slow = slow->next;
if (fast == slow) {
break;
}
}
if (fast == NULL || fast->next == NULL) {
return NULL;
}
slow = head;
while (fast != slow) {
fast = fast->next;
slow = slow->next;
}
return fast;
}
那么这个方法的原理是什么呢?我们证明一下,如下图:
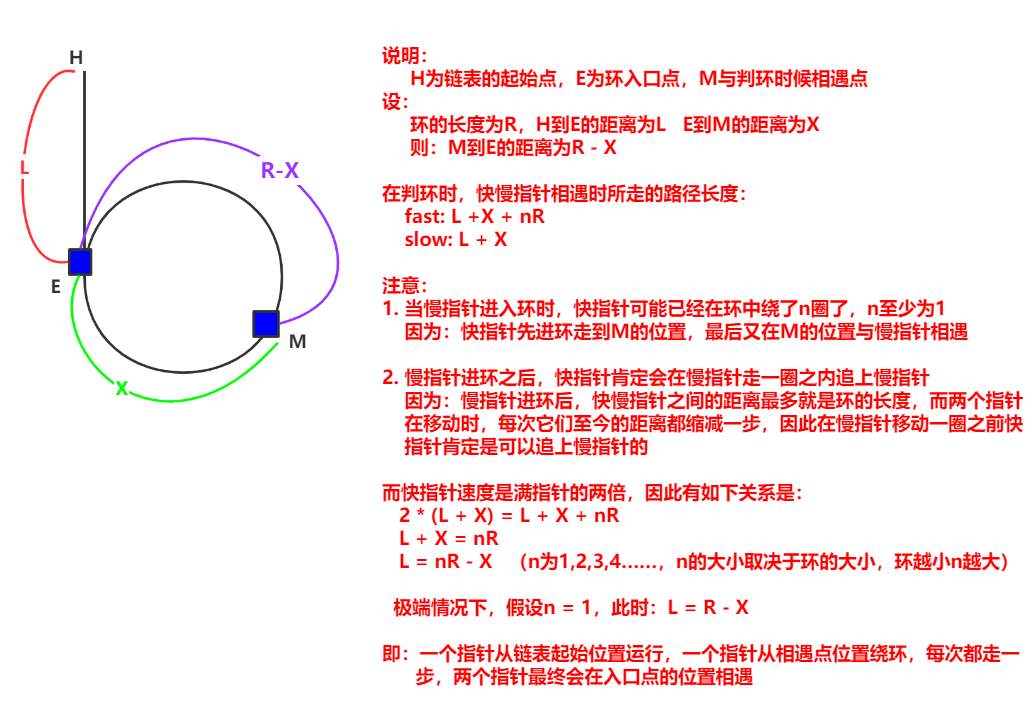
本题讲解到此为止。
六、链表算法OJ题:随机链表的复制
我先把题目的测试链接粘贴在下面:
题目详细叙述如下:
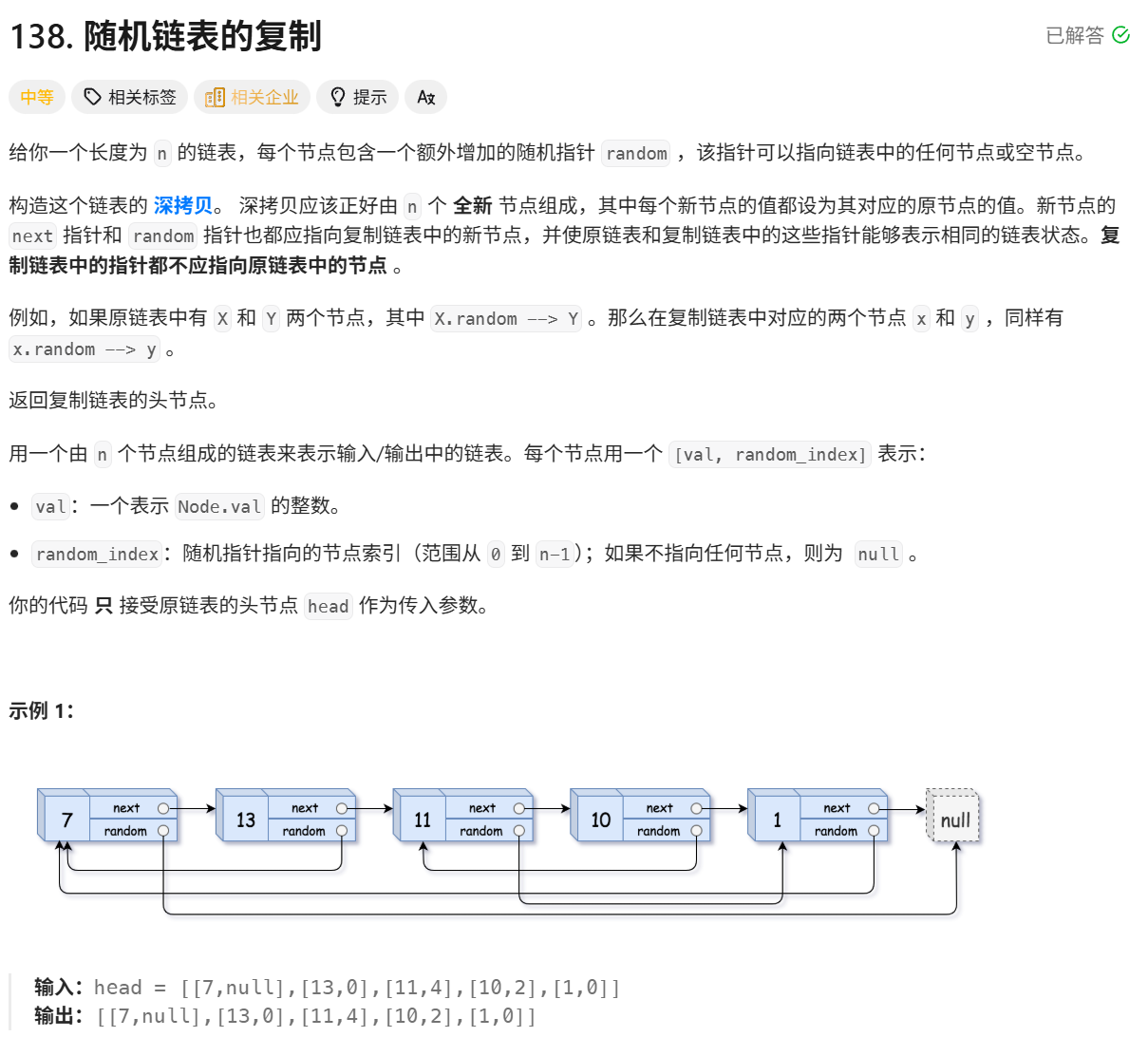
这道题需要采用三步插拆法实现带随机指针链表的深拷贝,核心利用将拷贝节点插入原节点后方的方式,避免额外空间存储节点映射关系,在O(n)时间复杂度和O(1)空间复杂度下完成拷贝。具体思路为首先遍历原链表,为每个原节点创建值相同的拷贝节点,并将拷贝节点插入到对应原节点的下一个位置,形成原节点与拷贝节点交替的链表结构;接着再次遍历原链表,根据原节点的random指针设置拷贝节点的random指针------若原节点random为空,拷贝节点random也为空,否则拷贝节点random指向原节点random所指节点的下一个拷贝节点;最后遍历链表,将插入的拷贝节点从原链表中拆分出来,通过copyhead和copytail构建独立的拷贝链表,同时恢复原链表的next指针结构,最终返回拷贝链表的头节点copyhead。我给出我的代码:
cpp
typedef struct Node Node;
struct Node* copyRandomList(struct Node* head) {
//第一步先是把拷贝节点插到被拷贝节点之后
Node* pcur = head;
while(pcur){
Node* copy = (Node*)malloc(sizeof(Node));
copy->val = pcur->val;
copy->next = pcur->next;
pcur->next = copy;
pcur = copy->next;
}
//第二步开始控制random
pcur = head;
while(pcur){
if(pcur->random == NULL){
pcur->next->random = NULL;
}else{
pcur->next->random = pcur->random->next;
}
pcur = pcur->next->next;
}
//第三步把拷贝节点拆分出去
pcur = head;
Node* copyhead = NULL;
Node* copytail = NULL;
pcur = head;
while(pcur){
Node* copy = pcur->next;
Node* next = copy->next;
if(copytail == NULL){
copyhead = copytail = copy;
}else{
copytail->next = copy;
copytail = copytail->next;
}
pcur->next = next;
pcur = next;
}
return copyhead;
}
本题讲解到此为止。
总结
本文介绍了5道链表相关算法题的解法:返回链表倒数第k个节点的两种方法(两次遍历法和快慢指针法);判断链表回文结构的实现思路(反转后半部分比对);寻找两个链表相交节点的长度差法;检测环形链表的快慢指针法及其数学证明;复制带随机指针链表的插拆法。文章提供了详细的算法思路、代码实现和必要的数学证明,帮助读者掌握链表问题的常见解决技巧。所有题目均给出力扣/牛客的测试链接供练习。