数据结构二叉树之链式结构（3）（上）

个人主页：星轨初途

个人专栏：C语言，数据结构

前言

嗨٩(๑❛ᴗ❛๑)۶，我们在刚进行了解二叉树时就向大家讲解了二叉树有两种表示方法------顺序结构和链式结构，顺序结构在前面几篇就已经进行了讲解，那么今天我们来介绍二叉树的链式结构

本文相关知识传送门：函数的栈帧的创建和销毁（超详细版本图文丰富）

一、创建二叉树链式结构（用链表实现）

在学习二叉树的基本操作前，需先要创建一棵二叉树，然后才能学习其相关的基本操作。

1、二叉树结构的创建

我们用链表来实现二叉树，相当于用链表来表示二叉树节点之间的关系，因为为二叉树，所以我们这里
用data表示当前节点数据
用指针left表示左孩子，也就是左节点
用指针right表示右孩子，也就是右节点

其结构代码如下

c 复制代码

#include <stdio.h>
#include <assert.h>
typedef int BTDataType;
//二叉树
typedef struct BinaryTreeNode
{
	BTDataType data;//当前节点数据
	struct BinaryTree* left; //当前结点指向的左子树地址
	struct BinaryTree* right;//当前结点指向的右子树地址
}BTNode;

2、手动创建链式二叉树

由于现在大家对二叉树结构掌握还不够深入，为了降低大家学习成本，此处手动快速创建一棵简单的二叉树，快速进入二叉树操作学习 ，等二叉树结构了解的差不多时，我们反过头再来研究二叉树真正的创建方式。

这里我们以下图为例，创建一个简单的链式二叉树

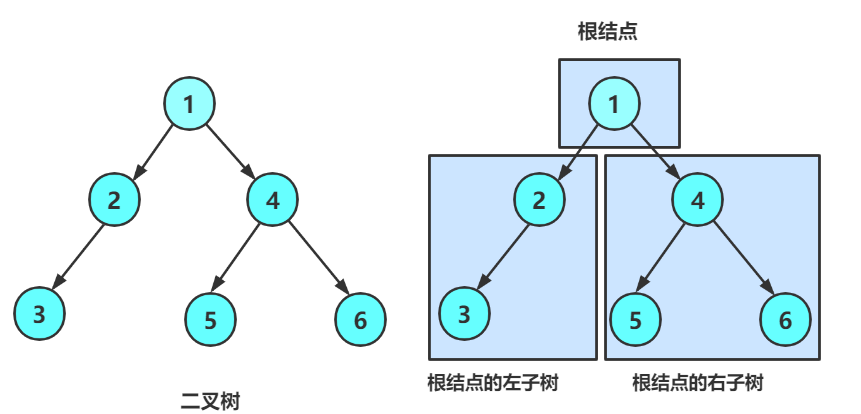
c 复制代码

#include<stdio.h>
typedef int BTDataType;
typedef struct BinaryTreeNode
{
	BTDataType data;
	struct BinaryTreeNode* left;
	struct BinaryTreeNode* right;
}BTNode;

BTNode* BuyNode(int x)
{
	BTNode* node = (BTNode*)malloc(sizeof(BTNode));
	if (node == NULL)
	{
		perror("malloc fail");
		return NULL;
	}
	node->data = x;
	node->left = NULL;
	node->right = NULL;
	return node;
}
BTNode* CreatBinaryTree()
{
	BTNode* node1 = BuyNode(1);
	BTNode* node2 = BuyNode(2);
	BTNode* node3 = BuyNode(3);
	BTNode* node4 = BuyNode(4);
	BTNode* node5 = BuyNode(5);
	BTNode* node6 = BuyNode(6);
	
	node1->left = node2;
	node1->right = node4;
	node2->left = node3;
	node4->left = node5;
	node4->right = node6;

	return node1;
}
int main()
{
	BTNode* root = CreatBinaryTree();
	return 0;
}

注意：上述代码并不是创建二叉树的方式，真正创建二叉树方式后序详解重点讲解。

再看二叉树基本操作前，再回顾下二叉树的概念，

二叉树是：

空树
非空：根结点，根结点的左子树、根结点的右子树组成的。
而左子树和右子树也是由左右子树节点和根节点组成，从概念中可以看出，二叉树定义是递归式的，因此后序基本操作中基本都是按照该概念实现的。

二、二叉树的遍历

二叉树的操作离不开树的遍历，让我们看看都有哪些遍历方式吧！

1、遍历规则

按照规则，二叉树的遍历有：前序、中序、后序的递归结构遍历 ：

（1）前序遍历(Preorder Traversal亦称先序遍历)------访问根结点的操作发生在遍历其左右子树之前。
访问顺序：根节点，左子树，右子树

（2）中序遍历(Inorder Traversal)------访问根结点的操作发生在遍历其左右子树之中（间）。
访问顺序：左子树，根节点，右子树

（3）后序遍历(Postorder Traversal)------访问根结点的操作发生在遍历其左右子树之后。
访问顺序：左子树，右子树，根节点

相当于就是根的访问顺序不同

2、前序遍历

（1）前序遍历思路

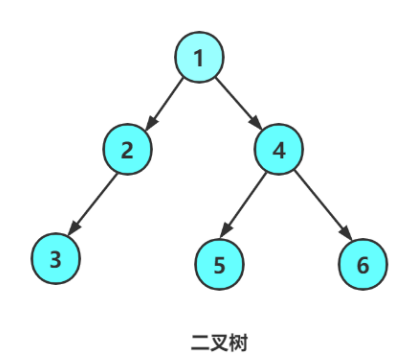
我们对这个进行分析，对它进行前序遍历，我们可以通过下面这张图来理解，序号表示递归顺序，逻辑就是根节点->左子树->右子树，若子树不为空，就先访问它的根节点->左子树->右子树，直到为空，再回去继续另一个子树

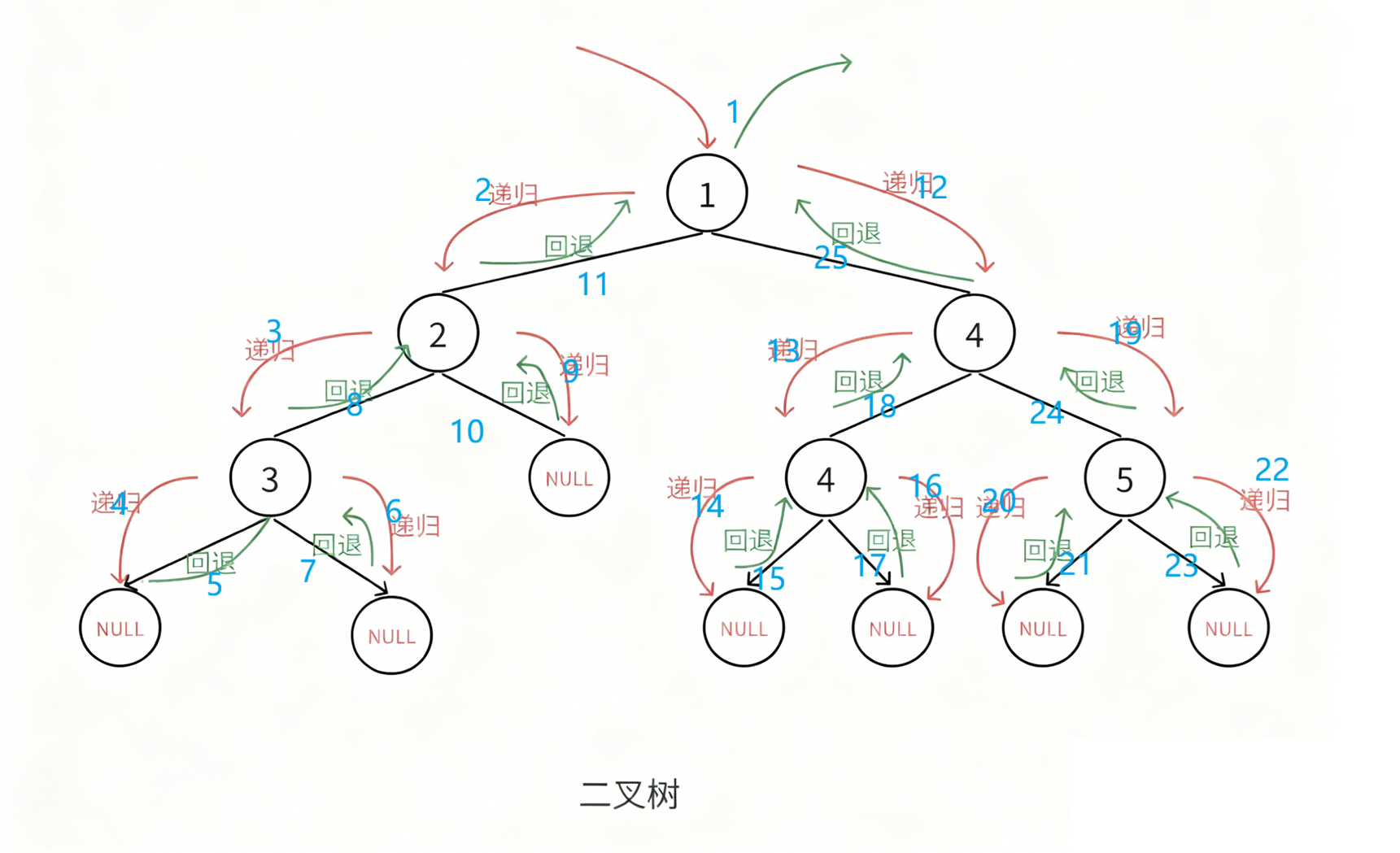
按照我们的思路结果应该如下，N表示空指针

下面我们使用代码实现

（2）代码实现

按照前面的思路我们来使用代码实现，这里空用N表示

这里只展示前序遍历代码，前面构建链式结构代码就不展示了

代码如下:

c 复制代码

void PrevOrder(BTNode* root)
{
	if (root == NULL)
	{
		printf("N ");
		return;
	}

	printf("%d ", root->data);
	PrevOrder(root->left);
	PrevOrder(root->right);
}
int main()
{
	BTNode* root = CreatBinaryTree();
	PrevOrder(root);
	return 0;
}

结果，与我们的思路一致，正确

2、中序遍历

同理，中序遍历就是左子树->根节点->右子树

所以只需把打印放在中间就行啦

c 复制代码

void InOrder(BTNode* root)
{
	if (root == NULL)
	{
		printf("N ");
		return;
	}

	InOrder(root->left);
	printf("%d ", root->data);
	InOrder(root->right);
}
int main()
{
	BTNode* root = CreatBinaryTree();
	InOrder(root);
	return 0;
}

结果

这里就不再做介绍了

3、后序遍历

就是左子树->右子树->根节点

代码

c 复制代码

//后序遍历------左右根
void PostOrder(BTNode* root)
{
	if (root == NULL)
	{
		printf("N ");
		return;
	}
	PostOrder(root->left);
	PostOrder(root->right);
	printf("%d ", root->data);
}
int main()
{
	BTNode* root = CreatBinaryTree();
	PostOrder(root);
	return 0;
}

结果

三、结束语

本篇到这里就结束啦ヾ(◍°∇°◍)ﾉﾞ，可能篇幅有些短，本文主要讲了二叉树链式结构的实现及二叉树遍历的规则及实现，下一篇我们就要将链式二叉树功能的相关实现和判断，欢迎大家来阅读！感谢大家的支持啦！