持续记录更新
前缀和
目的 :用于快速求解数组或矩阵中连续子区间的和。它的核心思想是预处理,通过一次遍历提前计算出一个辅助数组(前缀和数组),从而将后续的每次区间和查询时间从 O (n) 降低到 O (1)。
一维前缀和
定义一个一维数组 arr,其前缀和数组 preSum 的定义如下:
cpp
preSum[0] = 0
preSum[i] = arr[0] + arr[1] + ... + arr[i-1] (即前 i 个元素的和)
preSum[i] = arr[i-1] + preSum[i-1]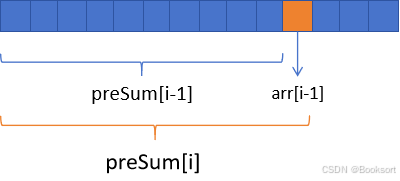
利用前缀和数组,可以快速计算出原数组中从索引 l 到 r(包含 l 和 r)的子区间和:
cpp
sum(l, r) = preSum[r+1] - preSum[l]例子
bash
假设 arr = [1, 2, 3, 4, 5]
前缀和数组 preSum 计算如下:
preSum[0] = 0
preSum[1] = 1
preSum[2] = 1+2 = 3
preSum[3] = 1+2+3 = 6
preSum[4] = 1+2+3+4 = 10
preSum[5] = 1+2+3+4+5 = 15
若要计算 arr[1] 到 arr[3] 的和(即 2+3+4):
sum(1, 3) = preSum[4] - preSum[1] = 10 - 1 = 9二维前缀和
preSum[i][j]表示矩阵中从(0,0) 到 (i-1,j-1)的子矩阵的和
cpp
preSum[i][j] = matrix[i-1][j-1] + preSum[i-1][j] + preSum[i][j-1] - preSum[i-1][j-1](重叠)
当前单元格的值 + 上方子矩阵和 + 左方子矩阵和 - 重复计算的左上子矩阵和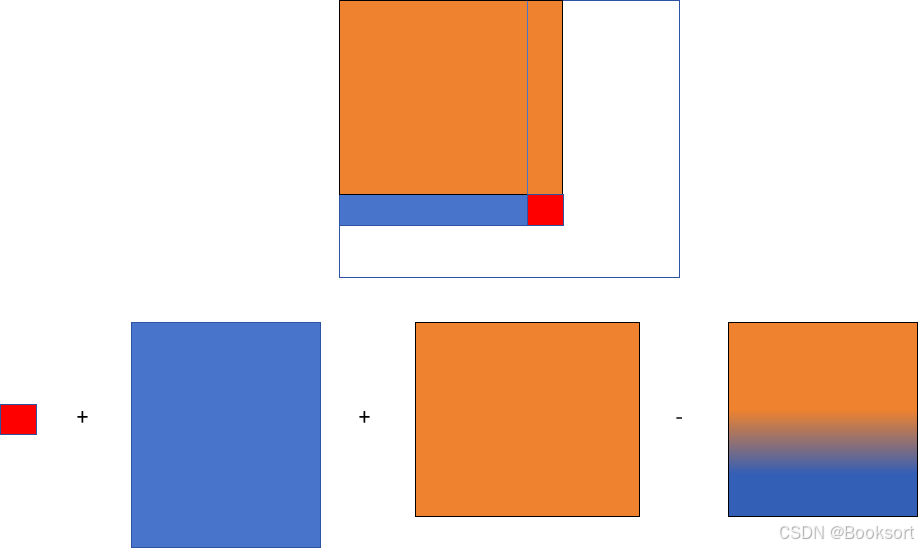
cpp
查询公式
若要计算从 (x1,y1) 到 (x2,y2) 的子矩阵和(包含边界):
sum = preSum[x2+1][y2+1] - preSum[x1][y2+1] - preSum[x2+1][y1] + preSum[x1][y1]
python
def prefix_sum_2d(matrix):
if not matrix or not matrix[0]:
return []
rows, cols = len(matrix), len(matrix[0])
pre_sum = [[0]*(cols+1) for _ in range(rows+1)]
for i in range(1, rows+1):
row_sum = 0
for j in range(1, cols+1):
row_sum += matrix[i-1][j-1]
pre_sum[i][j] = pre_sum[i-1][j] + row_sum
return pre_sum
# 示例
matrix = [[1, 2, 3], [4, 5, 6], [7, 8, 9]]
pre_sum_2d = prefix_sum_2d(matrix)
print(pre_sum_2d)
# 输出:
# [
# [0, 0, 0, 0],
# [0, 1, 3, 6],
# [0, 5, 12, 21],
# [0, 12, 27, 45]
# ]
# 查询子矩阵 (1,1) 到 (2,2) 的和
x1, y1 = 1, 1
x2, y2 = 2, 2
print(pre_sum_2d[x2+1][y2+1] - pre_sum_2d[x1][y2+1] - pre_sum_2d[x2+1][y1] + pre_sum_2d[x1][y1]) # 输出: 28前缀和优化的应用场景
- 频繁查询区间和:当需要多次查询数组或矩阵中不同子区间的和时,前缀和优化能显著提升效率。
- 滑动窗口问题:在滑动窗口类题目中,前缀和可用于快速计算窗口内元素的和。
- 动态规划:某些动态规划问题中,状态转移方程可能涉及区间和,前缀和可用于优化计算
例题1:统计稳定子数组的数目

1、分析题目,定义稳定子数组,即一个非递减区间的子数组 ,一个数组中,有很多块非递减区间的子数组,需要找找各个子数组是否符合非递减的特性
2、怎么统计非递减子数组的子集个数,1+2+3+...+N=N*(N+1)/2
3、判断左右区间覆盖的可能性:1、在一个非递减区间中;2、跨越一个或多个非递减区间
4、寻找规律并计算,这两种可能的计算出来的稳定子数组的个数
5、利用前缀和进行优化,否则超时
本题,统计左右区间覆盖中子数组的个数
情况一:[l,r]在一个非递减区间中

稳定子数组的计算公式为 N = R − L + 1 N=R-L+1 N=R−L+1, N ∗ ( N + 1 ) 2 \frac{N *(N+1)}{2} 2N∗(N+1)
关键是判断出这个稳定子数组中有多少个元素
情况二:[l,r]存在跨1个或多个非递减区间

前缀数组计算公式stable_arr[i] = nums[i]>=nums[i-1] ? stable_arr[i-1] + 1: 1;,计算从临界点开始重新计算存在的稳定子数组
不能直接计算前缀和,因为每次遇到分界点是会重新计算单个元素值,可以额外开一个数组计算前缀和presum_arr[i] = presum_arr[i-1] + stable_arr[i]
使用一个next数组,可以快速找到情况2的left的第一个分界点,不然在q循环中遍历去查找分界点,会超时
cpp
class Solution {
public:
vector<long long> countStableSubarrays(vector<int>& nums, vector<vector<int>>& queries) {
int N = nums.size();
vector<long long> ret_arr;
vector<long long> stable_arr(N,0);
vector<long long> presum_arr(N,0);
vector<int> next(N,0);
stable_arr[0]=1;
presum_arr[0] = stable_arr[0];
next[N-1] = N-1;
for(int i=1;i<nums.size();i++) {
stable_arr[i] = nums[i]>=nums[i-1] ? stable_arr[i-1] + 1: 1;
next[N-1-i] = nums[N-1-i]<=nums[N-i]? next[N-i]:N-1-i;
presum_arr[i] = presum_arr[i-1] + stable_arr[i];
}
for(int i=0;i<queries.size();i++) {
int left = queries[i][0];
int right = queries[i][1];
long long ret = 0;
int j = min(next[left],right)+1;
int m = j - left;
ret += (long long) (m*0.5*(m+1));
if(j<=right) {
//cout<<presum_arr[right] - presum_arr[j]+1<<" "<<accumulate(stable_arr.begin()+j, stable_arr.begin()+right+1, 0)<<endl;
//用前缀和优化,直接相加会超时
ret += presum_arr[right] - presum_arr[j]+1;//accumulate(stable_arr.begin()+j, stable_arr.begin()+right+1, 0);
}
ret_arr.push_back(ret);
}
return ret_arr;
}
};例题2:连接非零数字并乘以其数字和 II

本题与例题2同样的类型,都是需要在区间中频繁的去查找运算,还是需要
预处理+区间运算分析问题,改如何进行预处理,利用前缀和
- 计算区间内有效字符的数字和
- 计算区间内有效字符的×10和
直接理解,就是找到区间内的有效字符,然后挨个×10+value并且计算和,但是频繁的区间计算,在q循环中使用遍历查找,必然超时。
有效字符的数字和可以使用前缀和,直接可以得出,关键是第二个,区间内有效字符的×10和,
使用前缀,preMul[i]标识[0,i]中有效字符的数字乘积
如何处理[i,j]区间的数字乘积,想到的是preMul[j]-preMul[i-1]*1e(有效字符数)
本题出现了取MOD操作,需要,在每次运算时%MOD,尤其是1e(有效字符数),为了等式有效性,需要在每次×10都%MOD
cpp
class Solution {
const long long MOD = 1000000007;
public:
vector<int> sumAndMultiply(string s, vector<vector<int>>& queries) {
int N = s.size();
vector<int> preSum(N+1,0);//统计区间中有效数的和
vector<long long> preMul(N+1,0);//统计区间中有效数的乘积
vector<int> preCnt(N+1,0); //统计区间中存在几个有效字符
vector<long long> pow10(N+1,0);
pow10[0]=1;
for(int i=0;i<N;i++) {
preSum[i+1] = preSum[i] + (s[i]=='0'? 0:s[i]-'0');
preCnt[i+1] = preCnt[i] + (s[i]=='0'? 0: 1);
preMul[i+1] = (s[i]=='0'? preMul[i]:(long long)(preMul[i]*10 + s[i]-'0') % MOD);
pow10[i+1] = (pow10[i] * 10) % MOD;
//cout<<preSum[i+1]<<"-"<<preCnt[i+1]<<"-"<<preMul[i+1]<<endl;
}
vector<int> ret;
//通过前缀和预处理,频繁查询计算区间结果
for(int i=0;i<queries.size();i++) {
int left = queries[i][0];
int right = queries[i][1];
int cnt = preCnt[right+1] - preCnt[left];
long long x = (preMul[right+1] - preMul[left]*(pow10[cnt])) % MOD;
if(x<0) {
x += MOD;
}
int sum = preSum[right+1] - preSum[left];
long long ans = ((long long)sum*x) % MOD;
ret.push_back(ans);
}
return ret;
}
};回溯算法
子集型
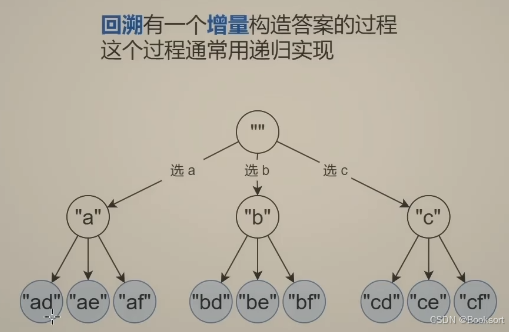
只需要把握边界条件 与非边界条件

需要理清楚,递归前进的状态(i->i+1,这个i具体是指什么,理清楚递归的时间线),递归终止条件与非终止条件的处理
例题

cpp
class Solution {
vector<string> arr = {"","","abc","def","ghi","jkl","mno","pqrs","tuv","wxyz"};
public:
void dfs(int i, int N,vector<string>& ans,string path,string& digits) {
if(i==N) { //终止条件
ans.push_back(path);
return;
}
//非终止条件,处理
for(auto e:arr[digits[i]-'0']) {
//增加新状态进入下一层递归/循环
dfs(i+1,N,ans,path + e,digits);
//恢复到原状态
}
}
vector<string> letterCombinations(string digits) {
vector<string> ans;
string s;
//递归的时间线i是指digits中的下标,挨个遍历,一层层向下去循环
dfs(0,digits.size(),ans,s,digits);
return ans;
}
};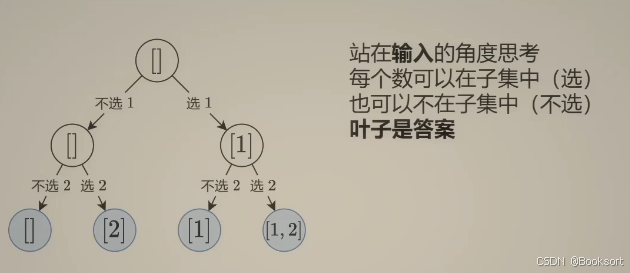

需要去构造哪些数可以选的判断条件,终止条件就是叶子节点
0-1选择递归
每一次递归,分别进行选择与不选的递归下一层,不选,就对答案不进行操作(充当一个跳过的作用),选择就append解
这个适合,每次新增状态都可以作为一个解进行记录,不适合需要全部遍历完才知道是否为解。
cpp
class Solution {
public:
void dfs(int i,int N,vector<int> path,vector<int>& nums,vector<vector<int>>& ans) {
if(i==N) {
ans.push_back(path);
return ;
}
dfs(i+1,N,path,nums,ans);//不选,充当一个跳过的作用
//选
path.push_back(nums[i]);
dfs(i+1,N,path,nums,ans);
path.pop_back();
}
vector<vector<int>> subsets(vector<int>& nums) {
int N=nums.size();
vector<int> path;
vector<vector<int>> ans;
dfs(0,N,path,nums,ans);
//ans.push_back(vector<int>());
return ans;
}
};
cpp
class Solution {
public:
bool ifPalindrome(string& s) {
int left=0;
int right = s.size()-1;
while(left<right) {
if(s[left]!=s[right]) return false;
left++;
right--;
}
return true;
}
vector<vector<string>> ret;
void dfs(int i, vector<string> ans, string& s,int j){
if(i==s.size()) {
ret.push_back(ans);
return ;
}
if(j==s.size()) return;//处理右边界,必须要返回上一层(j==N-1)去选择
//不选
dfs(i,ans,s,j+1);
string ts = s.substr(i,j-i+1);
if(ifPalindrome(ts)){
ans.push_back(ts);
dfs(j+1,ans,s,j+1);
ans.pop_back();
}
}
vector<vector<string>> partition(string s) {
vector<string> ans;
dfs(0,ans,s,0);
return ret;
}
};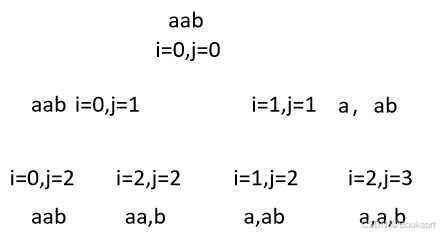
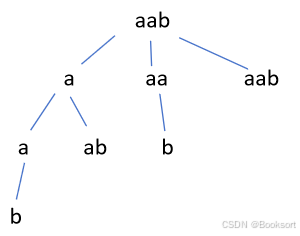
枚举递归
每一次必须选择一个,通过设置选择范围来进行每一层的筛选 ,每次选择都代表需要更新状态/解
这个适合,需要明确知道这一层的解是什么
c
class Solution {
public:
void dfs(int i,int N,vector<int> path,vector<int>& nums,vector<vector<int>>& ans) {
if(i==N) {
//ans.push_back(path);
return ;
}
for(int j = i;j<N;j++) {
path.push_back(nums[j]);
ans.push_back(path);//每出现一个新状态都需要append一次
dfs(j+1,N,path,nums,ans);
path.pop_back();
}
}
vector<vector<int>> subsets(vector<int>& nums) {
int N=nums.size();
vector<int> path;
vector<vector<int>> ans;
dfs(0,N,path,nums,ans);
ans.push_back(vector<int>());
return ans;
}
};
cpp
class Solution {
public:
bool ifPalindrome(string& s) {
int left=0;
int right = s.size()-1;
while(left<right) {
if(s[left]!=s[right]) return false;
left++;
right--;
}
return true;
}
vector<vector<string>> ret;
void dfs(int i, vector<string> ans, string& s){
if(i==s.size()) {
ret.push_back(ans);
return ;
}
for(int j=i;j<s.size();j++) {
string ts = s.substr(i,j-i+1);
if(ifPalindrome(ts)){
ans.push_back(ts);
dfs(j+1,ans,s);
ans.pop_back();
}
}
}
vector<vector<string>> partition(string s) {
vector<string> ans;
dfs(0,ans,s);
return ret;
}
};
组合型回溯
子集型回溯的一种剪枝
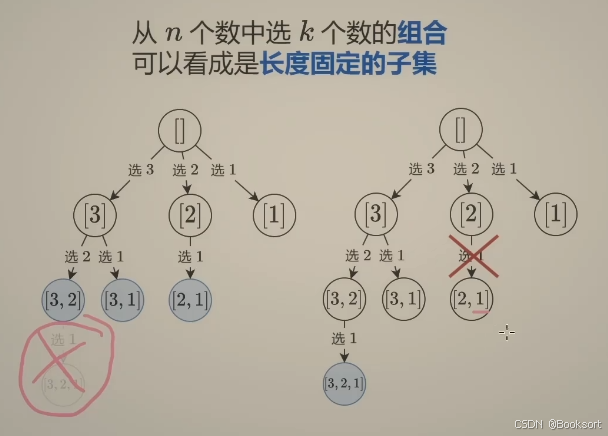
分析出剪枝条件,哪些条件可以返回,不用往下计算了
例题:组合

cpp
class Solution {
public:
vector<vector<int>> ans;
vector<int> path;
int sum=0;
void dfs(int i,int n,int k,int d) {
if(sum > n||path.size()>k) return; //超过了这个范围就返回
if(path.size()==k && sum==n) {
ans.push_back(path);
return ;
}
for(int j=i;j<=8;j++) {
if(9-j<d||n-sum<j) return; //剪枝,还剩下的几个数,剩下数的和是否有可能满足
path.push_back(j+1);
sum += j+1;
dfs(j+1,n,k,d-1);
path.pop_back();
sum-=j+1;
}
}
vector<vector<int>> combinationSum3(int k, int n) {
dfs(0,n,k,k);
return ans;
}
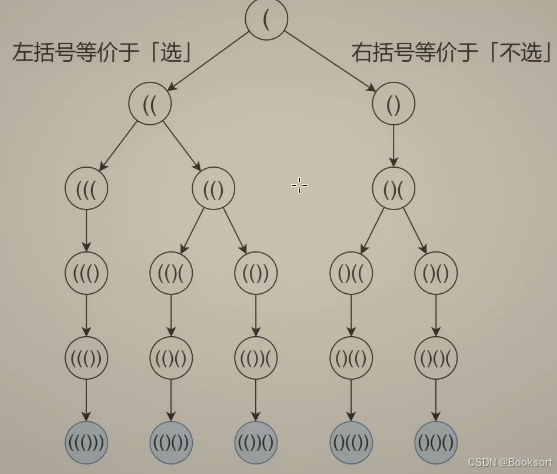
};例题:扩号生产

使用0-1选择的回溯模板,变成选'("与')',设置好剪枝条件
- count不会小于0,小于0说明当前括号不满足条件,不满足直接剪枝
- path长度为2N时判断是否满足
cpp
class Solution {
public:
vector<string> ans;
void dfs(int i,int count,int N,string path) {
/*
当i=0是一个空的
i=1时,才有第一个字符
当1=2*N时,path才刚好符合条件,会先去判断,才会考虑增加,不用担心,只需要确定好边界条件
*/
if(count<0) return;
if(i==2*N) {
if(count==0){
ans.push_back(path);
}
return ;
}
//选(
dfs(i+1,count+1,N,path+'(');
//选)
dfs(i+1,count-1,N,path+')');
}
vector<string> generateParenthesis(int n) {
string path;
dfs(0,0,n,path);
return ans;
}
};排列型回溯
全排列问题
dfs(遍历层的idx,未被选择的数字的集合)->子问题:dfs(遍历层的idx+1,未被选择的数字的集合)

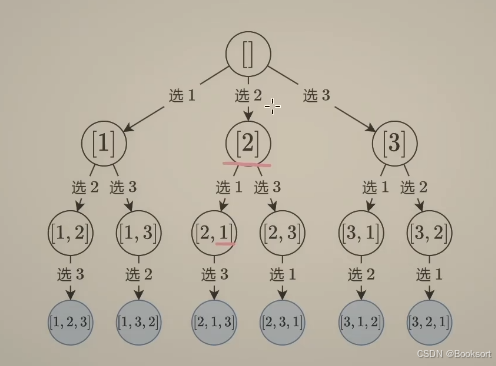
其时间复杂度是计算节点数*从根节点到叶子节点的长度= O ( N ∗ N ! ) O(N*N!) O(N∗N!)
N皇后问题
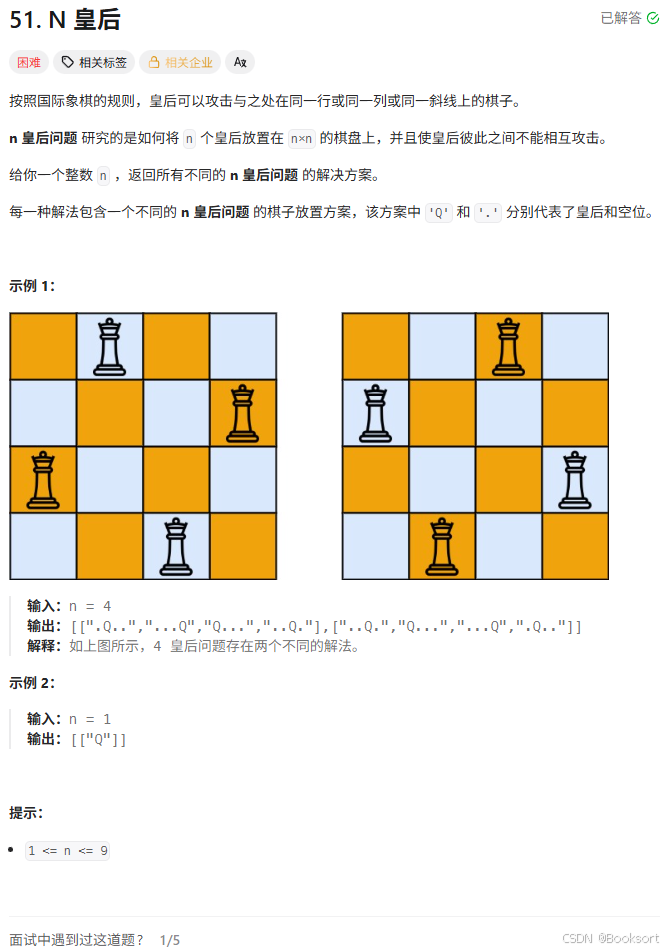
使用回溯法,利用递归来替代多重循环操作操作,转化为树模型进行求解。
- 先明确回溯的每一层,也就是i代表什么,可以设置为代表每一行的行号
- 明确求解的答案是列号,也就是说在递归时,行号是时间线,自动去递归迭代,然后去查找合法的列号,就能定位一个棋子的坐标
- 递归的边界条件,i==n,说明已经遍历了所有行,必须要剪枝,没有必要在进行递归了;合法解的条件,col_vec.size()==n,说明解是合法的
- 非边界条件,在[0,N-1]中进行遍历,如何这个列合法,就进行递归dfs(r+1),否者就跳过
N皇后判断一个列号是否合法:需要去遍历以及记录的位置,并挨个去判断是否满足y1-x1==y2-x2(正对角线) || x1+y1==x2+y2(反对角线) || x2==x2,只要符合,就说明这个列号不合法。时间复杂度为O(N)
通过一个函数去判断就比较简洁,如果使用一个set,每更新一个位置,就需要为下面的所有行都进行判断,判断每一行的哪些列号是不合法的,比较复杂。
也可以使用多个哈希表去分别记录,每个元素的x1+y1与x1-y1与x1,只需要通过三个哈希表的判断,就能把判断是否合法的时间复杂度 O ( N ) − > O ( 1 ) O(N)->O(1) O(N)−>O(1)
cpp
class Solution {
public:
vector<vector<int>> ans;
vector<int> path;
bool valid(int r,int c) {
//if(path.size()==0) return true;
//cout<<r<<","<<c<<endl;
for(int i=0;i<path.size();i++) {
//cout<<i<<","<<path[i]<<endl;
if(path[i]-i==c-r || path[i]+i==c+r ||c == path[i]) return false;
}
return true;
}
void dfs(int r,int n) {
//终止条件
//可用列数为0 return
// cout<<r<<"-"<<path.size()<<":";
// for(auto e:path){
// cout<<e<<" ";
// }
// cout<<endl;
if(r==n) {
if(path.size()==n) {
ans.push_back(path);
}
return;
}
for(int i=0;i<n;i++) {
if(!valid(r,i)) continue;
// cout<<r<<","<<i<<endl;
// for(auto e:path){
// cout<<e<<" ";
// }
// cout<<"----"<<endl;
path.push_back(i);
dfs(r+1,n);
path.pop_back();
}
}
vector<vector<string>> solveNQueens(int n) {
dfs(0,n);
vector<vector<string>> ret;
for(auto& path:ans) {
vector<string> tmp;
for(int i=0;i<path.size();i++) {
string s(n,'.');
s[path[i]]='Q';
tmp.push_back(s);
}
ret.push_back(tmp);
}
return ret;
}
};动态规划
关于动态规划问题,最基础/重要的是确定状态 与状态转移方程。
根据子集型回溯的0/1选择或选哪个的思路

这个问题从回溯的角度去思考
如果选择第一个房子,那么子问题变成了从n-2个房子中找最大的;
如果不选第一个房子,那么子问题变成了从n-1个房子中计算最大的;
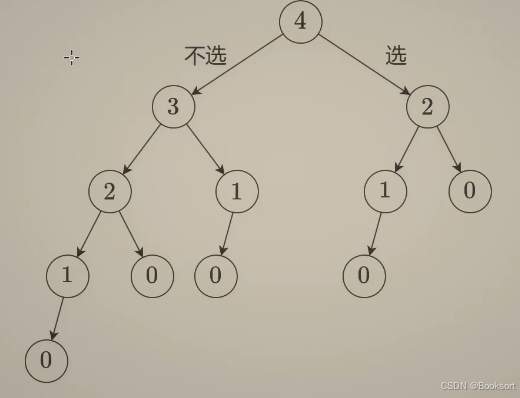
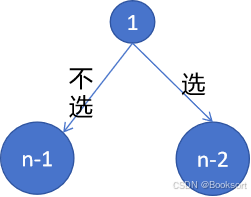
cpp
dfs(i) = max(dfs(i-1),dfs(i-2)+val[i])v1-回溯递归
cpp
class Solution {
public:
int dfs(int i,vector<int>& nums) {
if(i<0) return 0;
return max(dfs(i-1,nums), dfs(i-2,nums)+nums[i]);
}
int rob(vector<int>& nums) {
return dfs(nums.size()-1,nums);
}
};这个是递归回溯代码,但是会超时,因为每计算一个根节点,都要重复去递归计算地下的所有子节点,会非常耗时,使用一个容器,去记录,已经计算过的节点的值,就不需要重复去计算
v2-回溯+记忆化搜索
使用了一个哈希表去记录,并且会在去查找前进行判断哈希表中是否存在,时间复杂度为O(n)=状态个数*单个状态的计算时间
空间复杂度为O(N),自顶向下的递归需要开辟空间
cpp
class Solution {
public:
unordered_map<int,int> arr;
int dfs(int i,vector<int>& nums) {
if(i<0) return 0;
int res;
if(arr.find(i)!=arr.end()){
res = arr[i];
} else{
res = max(arr.find(i-1)==arr.end()?dfs(i-1,nums):arr[i-1], (arr.find(i-2)==arr.end()?dfs(i-2,nums):arr[i-2]) + nums[i]);
arr[i]=res;
}
return res;
}
int rob(vector<int>& nums) {
return dfs(nums.size()-1,nums);
}
};- 自顶向下:递归+记忆化搜索
- 自底向上:递推,从最低节点向上计算
将回溯递归+记忆化搜索,改成递推计算,回溯中,使用栈进行保存计算结果,递推中,使用数组保存结果
cpp
dfs(i) = max(dfs(i-1),dfs(i-2)+val[i])//使用栈保存结果
||
arr[i] = max(arr[i-1],arr[i-2]+val[i])//使用数组保存结果不过需要提前设置好,0-1与0-2的初始值,就像在递归中也通过判断条件设置了if(i<0) return 0;
所以创建一个N+2的数组,提前初始好0,遍历时(开始递归时)从i=[2,N+2)开始遍历
v3-自底向上递推
cpp
class Solution {
public:
int rob(vector<int>& nums) {
int N = nums.size();
vector<int> arr(N+2,0);//代表[0,i]个房子累计获得最大的金额
for(int i=2;i<N+2;i++) {
arr[i] = max(arr[i-1],arr[i-2]+nums[i-2]);
}
return *(arr.end()-1);
}
};但此时空间复杂度任然是O(N)因为使用了一个N的数组
不过可以通过公式分析得出,计算arr[i],只需要arr[i-1]与arr[i-2],i-2之前的所有元素都不需要被使用了,所以只需要递推式保存,上一个与上上一个元素的值即可。
v4-斐波那契数列
变成斐波那契数列了
cpp
class Solution {
public:
int rob(vector<int>& nums) {
//斐波那契数列
int N = nums.size();
int f1=0;//前一个
int f2=0;//前前一个
int f3;
for(int i=0;i<N;i++) {
f3 = max(f1,f2+nums[i]);
f2=f1;
f1=f3;
}
return f3;
}
};背包问题
0-1背包

在确定状态时,也需要确定状态转移的时间线,即i->i+1代表着什么含义
在背包问题中,i代表第i个物品,选择哪些物品,就是代表,哪些物品选或不选(0-1选择)
当前问题:在容量为capacity时,n个物品中价值最大,problem(n,capacity)
这个问题中,状态变化就是,当前第i个物品,选还是不选,会引发状态发生改变
下一个子问题:第i个物品不选:problem(i-1,c)的最大价值;第i个物品选:problem(i-1,c-c[i])+v[i]的最大价值,
状态转移方程:problem(i,c) = max(problem(i-1,c),problem(i-1,c-c[i])+[i])
当然,必须要满足c>=0的情况

例题:目标和

一眼分析,可以使用一个0-1子集回溯算法,每次要么选+,要么选-。
构建递归公式dfs(i,target) 代表,i个数,构成目标target的方案总数
cpp
dfs(i,target) = dfs(i-1,target+nums[i]) + dfs(i-1,target-nums[i])//-与+边界条件,当i<0的情况就是说明已经遍历结束了,递归的范围是[0,N-1],如果递归回到target==0,就说明是一个合法方案,方案数+1
cpp
class Solution {
public:
int dfs(int i,vector<int>& nums,int target) {
if(i<0) {
if(target==0) return 1;
return 0;
}
return dfs(i-1,nums,target-nums[i]) + dfs(i-1,nums,target+nums[i]);
}
int findTargetSumWays(vector<int>& nums, int target) {
return dfs(nums.size()-1,nums,target);
}
};也可以转换成0-1背包问题,使用动态规划
设数组中所有合法方案的正数和为p,则负数和为sum-p,有 t a r g e t = p − s u m + p − > p = t a r g e t + s u m 2 target=p-sum+p->p=\frac{target+sum}{2} target=p−sum+p−>p=2target+sum。
且p是一个正整数,必须要满足条件p>=0,并且p%2==0,如果不符合这个条件,就可以直接返回0
然后,问题就变成了,{arr1,arr2,...}数组中,那些数是组成p的,并且满足和为p
也就等效于一个0-1背包问题,恰好满足capacity,的方案数
cpp
class Solution {
public:
int findTargetSumWays(vector<int>& nums, int target) {
int sum = accumulate(nums.begin(),nums.end(),0);
int capacity = (sum - target);
//cout<<capacity<<endl;
if(capacity < 0 || capacity%2) return 0;
capacity /=2;
int N = nums.size();
vector<vector<int>> arr(N + 1, vector<int>(capacity + 1, 0));
//int arr[N+1][capacity+1] = {0}//arr[i][j]代表i个数字,组成capacity=j的方案数
arr[0][0] = 1;
for(int i=1;i<N+1;i++) {
for(int j=0;j<capacity+1;j++) {
if(j<nums[i-1])
arr[i][j] = arr[i-1][j];
else
arr[i][j] = arr[i-1][j] + arr[i-1][j-nums[i-1]];
//cout<<i<<","<<j<<"-"<<arr[i][j]<<endl;
}
}
return arr[N][capacity];
}
};还可以进一步分析空间复杂度,
由于公式计算中,只需要考虑第i个数组与第i-1个数组,之前的数组是不会被使用的,只需要创建两个n大小的数组即可
滚动数组

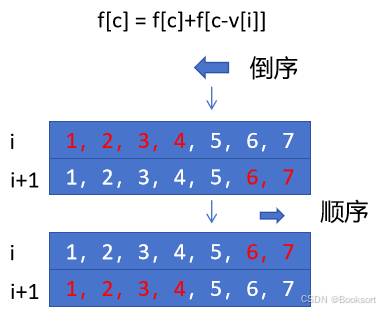
进一步优化,只使用一个数组,使用倒序遍历,从后往前遍历target
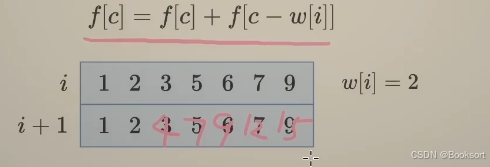
怎么判断优化成一个数组后,是顺序遍历还是倒序遍历?
cpp
class Solution {
public:
int findTargetSumWays(vector<int>& nums, int target) {
int sum = accumulate(nums.begin(),nums.end(),0);
int capacity = (sum - target);
//cout<<capacity<<endl;
if(capacity < 0 || capacity%2) return 0;
capacity /=2;
int N = nums.size();
//int arr[N+1][capacity+1] = {0}//arr[i][j]代表i个数字,组成capacity=j的方案数
vector<int> arr(capacity + 1, 0);
arr[0] = 1;
for(int i=1;i<N+1;i++) {
for(int j=capacity;j>=nums[i-1];j--) {//倒序,避免覆盖之前的值
arr[j] = arr[j] + arr[j-nums[i-1]];
//cout<<i<<","<<j<<"-"<<arr[i][j]<<endl;
}
}
return arr[capacity];
}
};完全背包

例题:零钱兑换

典型的完全背包问题
使用层次选择构建状态转移方程
dfs(amount)代表,构成amount最小需要的硬币数
cpp
dfs(amount) = min([dfs(coins[i]) for i in range(coins)])+1 设置边界条件,如果amount==0,就说明已经是合法的构成了,不会进一步递归,返回0
如果amount<0,就说明这条路径的组成不合法,返回INTMAX,这样与min最小化进行区分
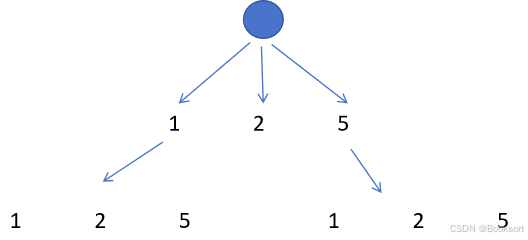
直接使用递归会超时,使用一个哈希表,进行记忆化搜索不会超时。
cpp
class Solution {
public:
unordered_map<int,int> umap;
int dfs(vector<int>& coins,int amount) {
if(amount<0) return INT_MAX;
if(amount==0) return 0;
int min_count = INT_MAX;
for(int i=0;i<coins.size();i++) {
min_count = min(umap.find(amount-coins[i])==umap.end()?dfs(coins,amount-coins[i]):umap[amount-coins[i]],min_count);
}
min_count = min_count==INT_MAX?INT_MAX:min_count+1;
umap[amount] = min_count;
return min_count;
}
int coinChange(vector<int>& coins, int amount) {
int ans = dfs(coins,amount);
return ans==INT_MAX?-1:ans;
}
};也可以转成0-1选择性
如果加入记忆化搜索,需要设置key={i,amount},记忆化搜索是为了缓存与快速查找之前递归已经计算的值,需要考虑不同环境下,必须要绑定i与amount,不然可能会互相覆盖。
cpp
class Solution {
public:
int dfs(int i,vector<int>& coins,int amount) {
if(i==coins.size()) {
if(amount==0) return 0;
return INT_MAX;
}
if(amount<coins[i]) return dfs(i+1,coins,amount);//跳过当前节点
int ans = dfs(i,coins,amount-coins[i]);
ans = ans==INT_MAX?INT_MAX:ans+1;
return min(dfs(i+1,coins,amount),ans);
}
int coinChange(vector<int>& coins, int amount) {
int ans = dfs(0,coins,amount);
return ans==INT_MAX?-1:ans;
}
};