目录
一、树的概念及结构
1.树的概念
树是一种非线性的数据结构。它由n(n>=0)个有限结点组成的一个具有层次关系的集合。
把它叫做树是因为它看起来像一棵倒置的树,也就是说它是根朝上、叶朝下的。

在树形结构中,子树之间不能有交集,否则就不是树结构。
除了根节点以外,每个节点有且只有一个父节点
一棵n个节点的树有(n-1)条边
2.树的相关概念
**节点的度:**一个节点含有的子树的个数称作该节点的度;如上图A的度是3。
**叶子节点或终端节点:**度为0的节点称为叶子节点;如上图K、L、F......等节点都是叶子节点
**非终端节点或分支节点:**度不为0的节点;如上图B、C、D......等节点为分支节点
**双亲节点或父节点:**若一个节点含有子节点,则这个结点称为其子节点的父节点;如上图A是B的父节点
**孩子节点或子节点:**一个节点含有的子树的根节点称为该节点的子节点;如上图B是A的子节点。
**兄弟节点:**具有相同父节点的节点互为兄弟节点;如上图B、C、D互为兄弟节点
**树的度:**一棵树中最大的结点的度称为树的度。例如上图树的度为3。
**节点的层次:**从根开始定义起,根为第一次层,根节点的子节点为第二层,以此类推。
**树的高度或深度:**树中节点的最大层次;如上图树的高度为4。
**堂兄弟结点:**双亲在同一层的结点互为堂兄弟;如上图E和G互为堂兄弟
**结点的祖先:**从根到该结点所经分支上的所有节点;如上图A是所有节点的祖先
**子孙:**以某节点为根的子树中任一节点都称为该节点的子孙,如上图所有节点都是A的子孙
**森林:**由m(m>0)棵互不相交的树组成的集合称为森林
3.树的表示
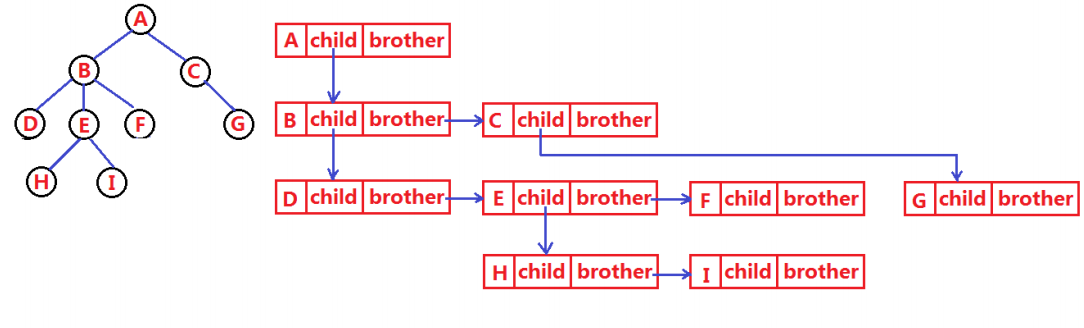
树有很多种表示方式,如:双亲表示法、孩子表示法、孩子双亲表示法以及孩子兄弟表示法。
二、二叉树概念及结构
1.概念
一棵二叉树是节点的一个有限集合,该节点:
(1)或为空
(2)由一个根节点加上左右两棵子树(左子树和右子树)组成

从上图可以看出:
(1)二叉树不存在度大于2的结点
(2)二叉树的子树有左右之分,次序不能颠倒,因此二叉树是有序树
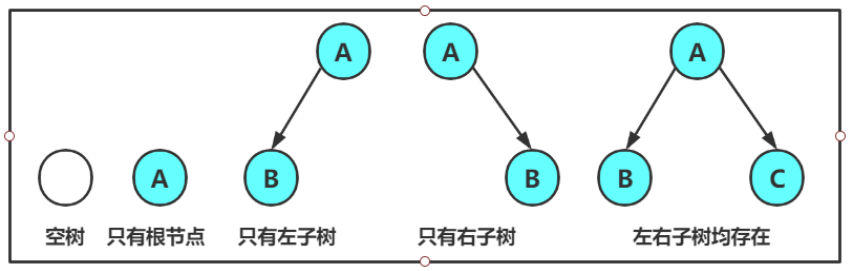
注意:对于任意的二叉树都是由以下几种情况复刻而成的:
2.特殊的二叉树
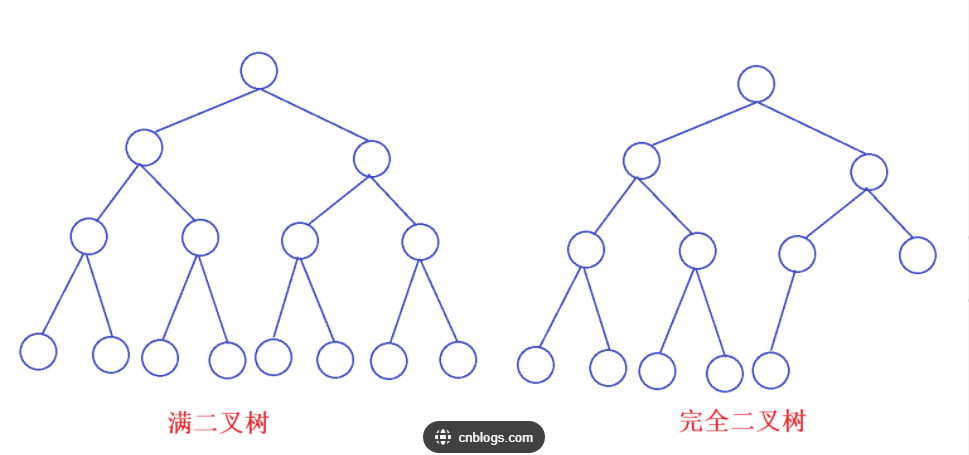
(1)满二叉树
一个二叉树,如果每一层的结点数量都达到最大值,则该二叉树为满二叉树。也就是说,如果一个高度为k的二叉树结点总数是(2^k-1),则它就是满二叉树。
(2)完全二叉树
完全二叉树是效率很高的数据结构。完全二叉树是由满二叉树引出来的。对于深度为k的二叉树,当且仅当其每个结点都与深度为k的满二叉树的编号一一对应时称其为完全二叉树。满二叉树是特殊的完全二叉树。
高度为k的完全二叉树中最少有2^(k-1)个节点。
3.二叉树的性质
(1)若规定根节点的层数为1,则一棵非空二叉树的第i层上最多有2^(i-1)个节点
(2)若规定根节点的层数为1,则深度为h的二叉树的最大节点数是2^h-1
(3)对任意一棵二叉树,如果度为0的叶子结点的个数为n0,度为2的分支节点的个数为n2,则n0 = n2 + 1
(4)若规定根节点的层数为1,具有n个节点的满二叉树的深度h = log2(n+1)
(5)对于具有n个节点的完全二叉树,如果按照从上至下从左至右的数组顺序对所有节点从0开始编号,则对于序号为i的节点有:
- 若i>0,i位置结点的双亲序号:(i-1)/2;i = 0时i为根节点,无双亲结点
- 若2i+1<n,左孩子序号:2i+1;2i+1>=n,否则无左孩子
- 若2i+2<n,左孩子序号:2i+2;2i+2>=n,否则无左孩子
4.二叉树的存储结构
(1)顺序存储
顺序存储就是用数组 来存储,一般使用数组只适合表示完全二叉树 ,因为不是完全二叉树会有空间的浪费。而现实中只有堆 才会使用数组存储。二叉树顺序存储在物理上是一个数组,在逻辑上是一棵二叉树。
(2)链式存储
二叉树的链式存储结构是指:用链表来表示一棵二叉树,即用链来指示元素的逻辑关系。通常的方法是链表中每个结点由三个域(数据域和左右指针域)组成,左右指针分别指向左右孩子所在的结点。链式结构分为二叉链和三叉链。
cpp
typedef int BTDataType;
// 二叉链
struct BinaryTreeNode {
struct BinaryTreeNode* left; // 指向当前结点的左孩子
struct BinaryTreeNode* right; // 指向当前结点的右孩子
BTDataType data; // 当前结点值域
};
// 三叉链
struct BinaryTreeNode {
struct BinaryTreeNode* parent; // 指向当前结点的双亲
struct BinaryTreeNode* left; // 指向当前结点的左孩子
struct BinaryTreeNode* right; // 指向当前结点的右孩子
BTDataType data; // 当前结点值域
};三、二叉树链式结构的实现
1.二叉树的创建
传入二叉树的前序遍历序列字符串和字符串大小、起始下标用来创建二叉树
函数声明
cpp
// 通过前序遍历的数组"ABD##E#H##CF##G##"构建二叉树
BTNode* BinaryTreeCreate(BTDataType* a, int n, int* pi);函数定义
cpp
// 通过前序遍历的数组"ABD##E#H##CF##G##"构建二叉树
BTNode* BinaryTreeCreate(BTDataType* a, int n, int* pi) {
if (*pi >= n || a[*pi] == '#')
{
(*pi)++;
return NULL;
}
BTNode* cur = (BTNode*)malloc(sizeof(BTNode));
cur->_data = a[*pi];
(*pi)++;
cur->_left = BinaryTreeCreate(a, n, pi);
cur->_right = BinaryTreeCreate(a, n, pi);
return cur;
}函数测试
cpp
char a[] = "ABD##E#H##CF##G##";
int i = 0;
BTNode* BinaryTree = BinaryTreeCreate(a, sizeof(a) / sizeof(a[0]), &i);2.二叉树销毁
二叉树的销毁要以后序的顺序销毁
函数声明
cpp
// 二叉树销毁
void BinaryTreeDestory(BTNode** root);函数定义
cpp
// 二叉树销毁
void BinaryTreeDestory(BTNode** root) {
if (*root) {
BinaryTreeDestory(&(*root)->_left);
BinaryTreeDestory(&(*root)->_right);
free(*root);
*root = NULL;
}
}3.二叉树的遍历
二叉树遍历(Traversal):按照某种特定的规则,依次对二叉树中的结点进行相应的操作,并且每个结点只操作一次。访问结点所做的操作依赖于具体的应用问题。遍历二叉树是二叉树上最重要的运算之一,也是二叉树上进行其他运算的基础。
二叉树的遍历有四种:前序遍历、中序遍历、后序遍历、层序遍历
- 前序遍历(Preorder Traversal 也叫先序遍历)------访问根节点的操作发生在遍历其左右子树之前(根左右)。
- 中序遍历(Inorder Traversal)------访问根节点的操作发生在遍历其左右子树之中(左根右)
- 后序遍历(Postorder Traversal)------访问根节点的操作发生在遍历其左右子树之后(左右根)
由于被访问的结点必须是某子树的根,所以**N(Node)、L(Left subtree)和R(Right subtree)又可解释为根、根的左子树、根的右子树。**NLR、LNR和LRN又称为先根遍历、中根遍历和后根遍历。
(1)前序遍历、中序遍历、后序遍历的递归实现
递归的本质是把问题拆成当前问题和子问题。
递归的返回条件本质是最小规模的子问题。
函数声明
cpp
// 二叉树前序遍历
void BinaryTreePrevOrder(BTNode* root);
// 二叉树中序遍历
void BinaryTreeInOrder(BTNode* root);
// 二叉树后序遍历
void BinaryTreePostOrder(BTNode* root);函数定义
cpp
// 二叉树前序遍历
void BinaryTreePrevOrder(BTNode* root) {
if (root == NULL) {
return;
}
printf("%c", root->_data);
BinaryTreePrevOrder(root->_left);
BinaryTreePrevOrder(root->_right);
}
// 二叉树中序遍历
void BinaryTreeInOrder(BTNode* root) {
if (root == NULL) {
return;
}
BinaryTreeInOrder(root->_left);
printf("%c", root->_data);
BinaryTreeInOrder(root->_right);
}
// 二叉树后序遍历
void BinaryTreePostOrder(BTNode* root) {
if (root == NULL) {
return;
}
BinaryTreePostOrder(root->_left);
BinaryTreePostOrder(root->_right);
printf("%c", root->_data);
}可以看到前序遍历、中序遍历、后序遍历的代码非常相似,只是递归调用的位置不同。
函数测试
cpp
BinaryTreePrevOrder(BinaryTree);
printf("\n");
BinaryTreeInOrder(BinaryTree);
printf("\n");
BinaryTreePostOrder(BinaryTree);
printf("\n");测试结果

(2)二叉树的层序遍历
层序遍历是从所在二叉树的根节点出发,从上到下从左到右依次访问每一层的每一个结点。
层序遍历的实现需要使用队列,上一层结点出队列时下一层结点入队列
4.二叉树结点个数
递归遍历二叉树,若当前结点为空则返回0,不为空则返回(左子树结点个数+右子树结点个数+1)
函数声明
cpp
// 二叉树节点个数
int BinaryTreeSize(BTNode* root);函数定义
cpp
// 二叉树节点个数
int BinaryTreeSize(BTNode* root) {
if (root == NULL) {
return 0;
}
int leftNum = BinaryTreeSize(root->_left);
int rightNum = BinaryTreeSize(root->_right);
return leftNum + rightNum + 1;
}函数测试
cpp
printf("%d\n", BinaryTreeSize(BinaryTree));5.二叉树叶子节点个数
递归遍历二叉树,若当前结点为空则返回0,当前结点为叶子节点则返回1,其他情况则返回(左子树叶子结点个数+右子树叶子结点个数)
函数声明
cpp
// 二叉树叶子节点个数
int BinaryTreeLeafSize(BTNode* root);函数定义
cpp
// 二叉树叶子节点个数
int BinaryTreeLeafSize(BTNode* root) {
if (root == NULL) {
return 0;
}
if (root->_left == NULL && root->_right == NULL) {
return 1;
}
int leftNum = BinaryTreeLeafSize(root->_left);
int rightNum = BinaryTreeLeafSize(root->_right);
return leftNum + rightNum;
}函数测试
cpp
printf("%d\n", BinaryTreeLeafSize(BinaryTree));6.二叉树第k层结点个数
当前结点为空时返回0;当k<0时无法查找,返回0;当k==1时说明当前结点就是第k层的结点,返回1;全部判断完毕后再依次遍历左右子树的k-1层,并分别记录左右子树第k层的结点数量(防止重复递归调用),最后返回(leftCount + rightCount)
函数声明
cpp
// 二叉树第k层节点个数
int BinaryTreeLevelKSize(BTNode* root, int k);函数定义
cpp
// 二叉树第k层节点个数
int BinaryTreeLevelKSize(BTNode* root, int k) {
if (root == NULL) {
return 0;
}
if (k < 0) {
return 0;
}
if (k == 1) {
return 1;
}
int leftCount = BinaryTreeLevelKSize(root->_left, k - 1);
int rightCount = BinaryTreeLevelKSize(root->_right, k - 1);
return leftCount + rightCount;
}函数测试
cpp
printf("%d\n", BinaryTreeLevelKSize(BinaryTree, 3));7.二叉树查找值为x的节点
遍历二叉树,当该节点为空时返回NULL,不为空时判断data是否与x相同,相同则返回root,不同则查找左右子树。
函数声明
cpp
// 二叉树查找值为x的节点
BTNode* BinaryTreeFind(BTNode* root, BTDataType x);函数定义
cpp
// 二叉树查找值为x的节点
BTNode* BinaryTreeFind(BTNode* root, BTDataType x) {
if (root == NULL) {
return NULL;
}
if (root->_data == x) {
return root;
}
else {
BinaryTreeFind(root->_left, x);
BinaryTreeFind(root->_right, x);
}
}函数测试
BinaryTreeFind返回的是BTNode*,所以需要通过判断返回值是否为空来判断是否找到值为x的结点。
cpp
BTNode* find = BinaryTreeFind(BinaryTree, 'C');
if (find) {
printf("%c\n", find->_data);
}
else {
printf("没有找到");
}8.完整代码
BinaryTree.h
cpp
#pragma once
#include<stdio.h>
#include<stdlib.h>
#include<assert.h>
typedef char BTDataType;
typedef struct BinaryTreeNode
{
BTDataType _data;
struct BinaryTreeNode* _left;
struct BinaryTreeNode* _right;
}BTNode;
// 通过前序遍历的数组"ABD##E#H##CF##G##"构建二叉树
BTNode* BinaryTreeCreate(BTDataType* a, int n, int* pi);
// 二叉树销毁
void BinaryTreeDestory(BTNode** root);
// 二叉树节点个数
int BinaryTreeSize(BTNode* root);
// 二叉树叶子节点个数
int BinaryTreeLeafSize(BTNode* root);
// 二叉树第k层节点个数
int BinaryTreeLevelKSize(BTNode* root, int k);
// 二叉树查找值为x的节点
BTNode* BinaryTreeFind(BTNode* root, BTDataType x);
// 二叉树前序遍历
void BinaryTreePrevOrder(BTNode* root);
// 二叉树中序遍历
void BinaryTreeInOrder(BTNode* root);
// 二叉树后序遍历
void BinaryTreePostOrder(BTNode* root);BinaryTree.c
cpp
#define _CRT_SECURE_NO_WARNINGS 1
#include"BinaryTree.h"
// 通过前序遍历的数组"ABD##E#H##CF##G##"构建二叉树
BTNode* BinaryTreeCreate(BTDataType* a, int n, int* pi) {
if (*pi >= n || a[*pi] == '#')
{
(*pi)++;
return NULL;
}
BTNode* cur = (BTNode*)malloc(sizeof(BTNode));
cur->_data = a[*pi];
(*pi)++;
cur->_left = BinaryTreeCreate(a, n, pi);
cur->_right = BinaryTreeCreate(a, n, pi);
return cur;
}
// 二叉树销毁
void BinaryTreeDestory(BTNode** root) {
if (*root) {
BinaryTreeDestory(&(*root)->_left);
BinaryTreeDestory(&(*root)->_right);
free(*root);
*root = NULL;
}
}
// 二叉树节点个数
int BinaryTreeSize(BTNode* root) {
if (root == NULL) {
return 0;
}
int leftNum = BinaryTreeSize(root->_left);
int rightNum = BinaryTreeSize(root->_right);
return leftNum + rightNum + 1;
}
// 二叉树叶子节点个数
int BinaryTreeLeafSize(BTNode* root) {
if (root == NULL) {
return 0;
}
if (root->_left == NULL && root->_right == NULL) {
return 1;
}
int leftNum = BinaryTreeLeafSize(root->_left);
int rightNum = BinaryTreeLeafSize(root->_right);
return leftNum + rightNum;
}
// 二叉树第k层节点个数
int BinaryTreeLevelKSize(BTNode* root, int k) {
if (root == NULL) {
return 0;
}
if (k < 0) {
return 0;
}
if (k == 1) {
return 1;
}
int leftCount = BinaryTreeLevelKSize(root->_left, k - 1);
int rightCount = BinaryTreeLevelKSize(root->_right, k - 1);
return leftCount + rightCount;
}
// 二叉树查找值为x的节点
BTNode* BinaryTreeFind(BTNode* root, BTDataType x) {
if (root == NULL) {
return NULL;
}
if (root->_data == x) {
return root;
}
else {
BinaryTreeFind(root->_left, x);
BinaryTreeFind(root->_right, x);
}
}
// 二叉树前序遍历
void BinaryTreePrevOrder(BTNode* root) {
if (root == NULL) {
return;
}
printf("%c", root->_data);
BinaryTreePrevOrder(root->_left);
BinaryTreePrevOrder(root->_right);
}
// 二叉树中序遍历
void BinaryTreeInOrder(BTNode* root) {
if (root == NULL) {
return;
}
BinaryTreeInOrder(root->_left);
printf("%c", root->_data);
BinaryTreeInOrder(root->_right);
}
// 二叉树后序遍历
void BinaryTreePostOrder(BTNode* root) {
if (root == NULL) {
return;
}
BinaryTreePostOrder(root->_left);
BinaryTreePostOrder(root->_right);
printf("%c", root->_data);
}Test.c
cpp
#define _CRT_SECURE_NO_WARNINGS 1
#include"BinaryTree.h"
void BTreeTest() {
char a[] = "ABD##E#H##CF##G##";
int i = 0;
BTNode* BinaryTree = BinaryTreeCreate(a, sizeof(a) / sizeof(a[0]), &i);
printf("%d\n", BinaryTreeSize(BinaryTree));
printf("%d\n", BinaryTreeLeafSize(BinaryTree));
printf("%d\n", BinaryTreeLevelKSize(BinaryTree, 3));
BTNode* find = BinaryTreeFind(BinaryTree, 'C');
if (find) {
printf("%c\n", find->_data);
}
else {
printf("没有找到");
}
BinaryTreePrevOrder(BinaryTree);
printf("\n");
BinaryTreeInOrder(BinaryTree);
printf("\n");
BinaryTreePostOrder(BinaryTree);
printf("\n");
BinaryTreeDestory(&BinaryTree);
}
int main() {
BTreeTest();
return 0;
}