基础数学算法-移棋子游戏

目录

• • 题目-移棋子游戏
  • 问题分析
  • 算法步骤
  • 代码实现

题目-移棋子游戏

问题分析

因为图上是没有环 的, 游戏一定会结束

问题的本质上就是 S G SG SG函数的定义
S G ( x ) = m e x { S G ( k ) } SG(x) = mex \{ SG(k)\} SG(x)=mex{SG(k)}

具体的定义和证明在基础数学算法的博弈论章节

假设当前有 k k k个棋子, 并且有 t t t个局面, 先手必胜等价于
S G ( s 1 ) ⊕ S G ( s 2 ) ⊕ S G ( s 3 ) ⊕ . . . ⊕ S G ( s t ) ≠ 0 SG(s_1) \oplus SG(s_2) \oplus SG(s_3) \oplus ... \oplus SG(s_t) \ne 0 SG(s1)⊕SG(s2)⊕SG(s3)⊕...⊕SG(st)=0

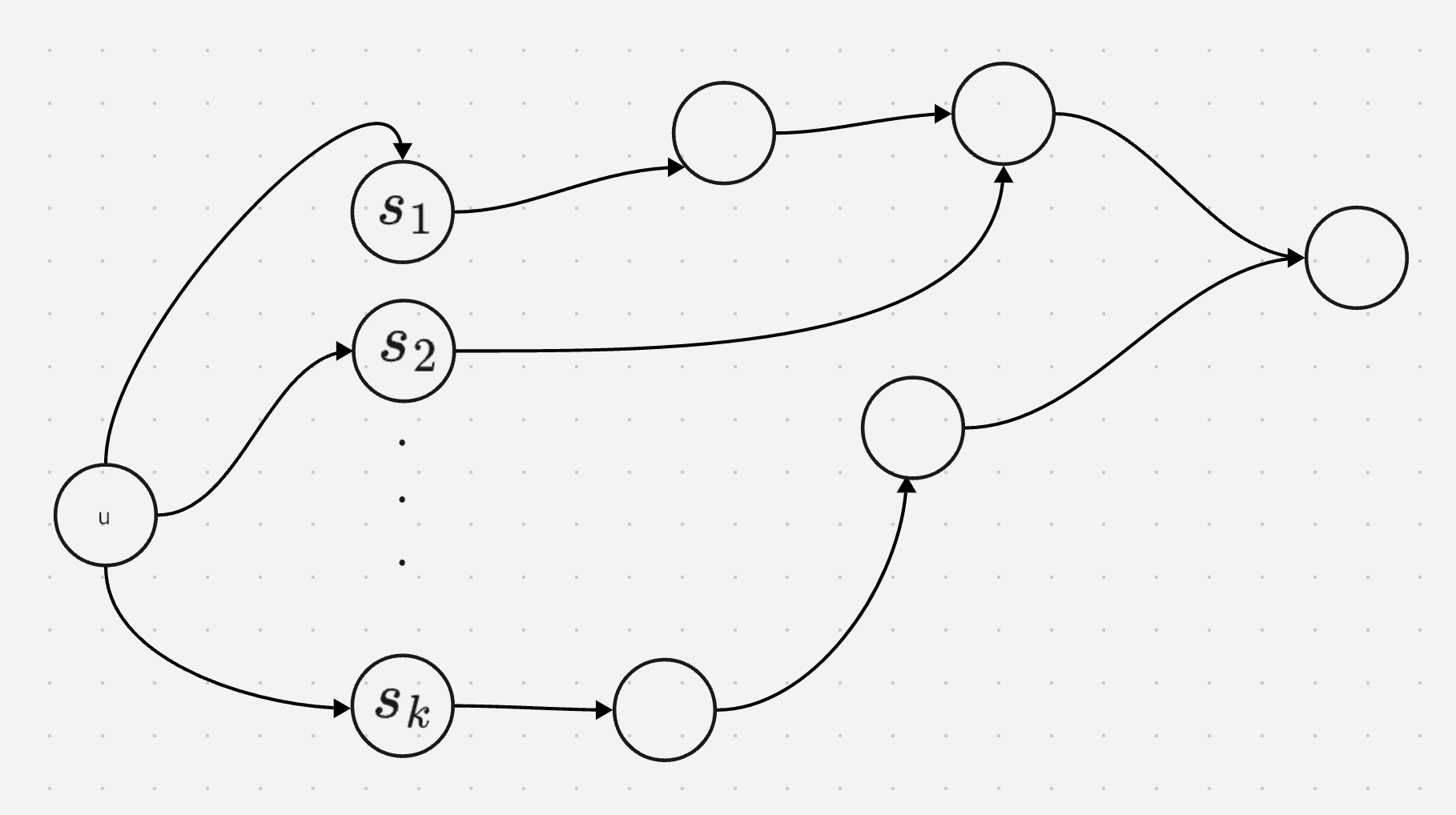
可以用记忆化搜索 计算每个节点的 S G SG SG值, 对于当前点 u u u, 可以先计算后面所有节点 的 S G SG SG的值存到一个集合当中 , 然后从 0 0 0开始计算 m e x ( u ) mex(u) mex(u)的值

算法步骤

每个点的后继元素数量其实是边的数量 M A MA MA, 需要枚举所有点 N N N, 算法时间的复杂度 O ( N + M ) O(N + M) O(N+M)

代码实现

#include <bits/stdc++.h>

using namespace std;

const int N = 2010, M = 6010;

int n, m, k;
int h[N], ed[M], ne[M], idx;
int f[N];

void add(int u, int v) {
    ed[idx] = v, ne[idx] = h[u], h[u] = idx++;
}

int sg(int x) {
    if (f[x] != -1) return f[x];

    set<int> s;
    for (int i = h[x]; ~i; i = ne[i]) {
        int v = ed[i];
        s.insert(sg(v));
    }

    for (int i = 0; ; ++i) {
        if (!s.count(i)) return f[x] = i;
    }
}

int main() {
    ios::sync_with_stdio(false);
    cin.tie(0);

    memset(h, -1, sizeof h);
    memset(f, -1, sizeof f);

    cin >> n >> m >> k;
    for (int i = 0; i < m; ++i) {
        int u, v;
        cin >> u >> v;
        add(u, v);
    }

    int ans = 0;
    for (int i = 0; i < k; ++i) {
        int u;
        cin >> u;
        ans ^= sg(u);
    }

    cout << (ans ? "win" : "lose") << '\n';

    return 0;
}