一、原理介绍
在进行参数辨识或者算法鲁棒性验证时,受困了MATLAB自带电机模型不方便运行中更改参数的问题,因此搭建一个可以设定参数变化的PMSM模型,并组建带有1.5拍数字延迟补偿的离散化矢量控制系统。
二、仿真模型
在MATLAB/simulink里面验证所提算法,搭建仿真。采用和实验中一致的控制周期1e-4,电机部分计算周期为1e-6。仿真模型如下所示:
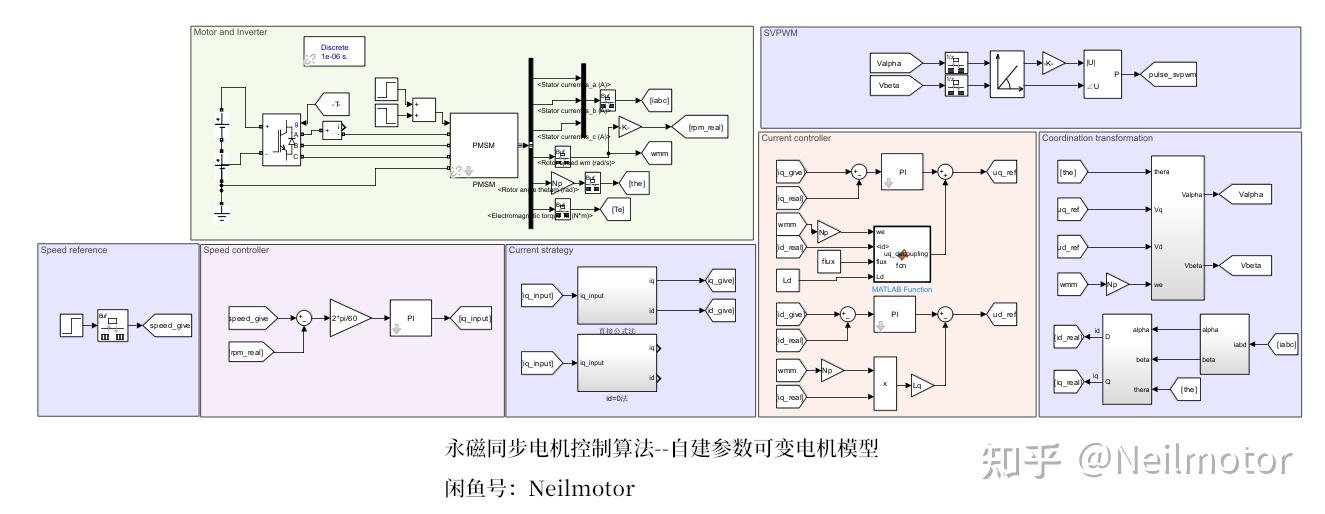
仿真工况1:电机空载零速启动,0s阶跃给定转速1000rpm,0.5s施加额定负载。电机参数保持固定值。
2.1给定转速、实际转速
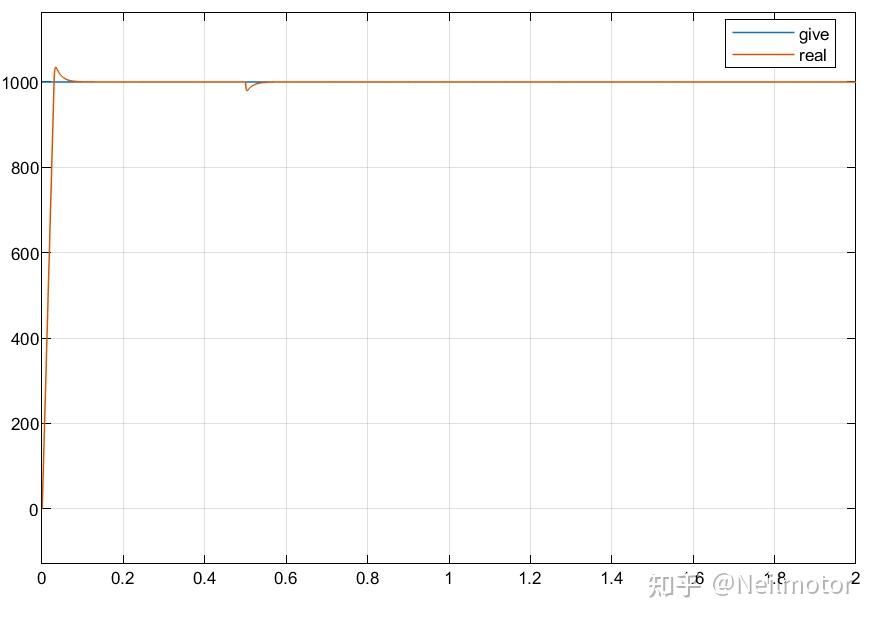
2.2dq轴电流
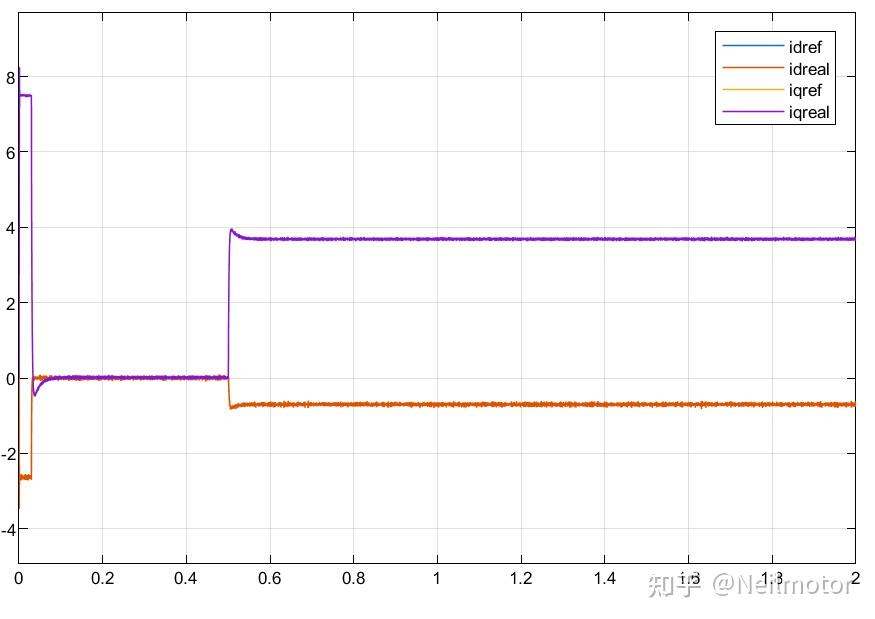
2.3dq轴给定电压
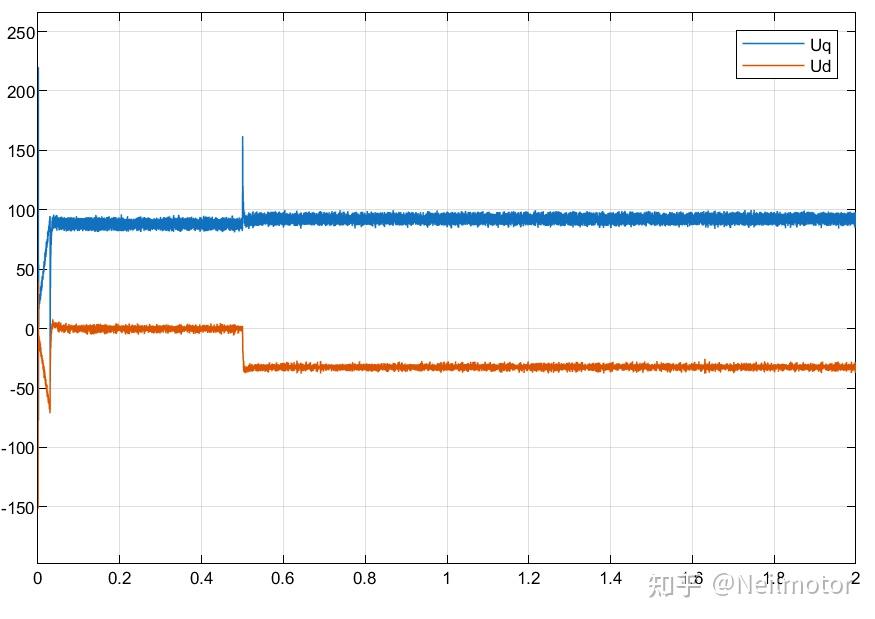
以上波形与使用MATLAB自带电机模型基本一致,电压波动略微是由于电流环带宽设置较大。
仿真工况2:电机空载零速启动,0s阶跃给定转速1000rpm,0.5s施加额定负载,1s时电阻逐渐增大至5倍额定值,其他参数保持不变。
2.4dq轴电流
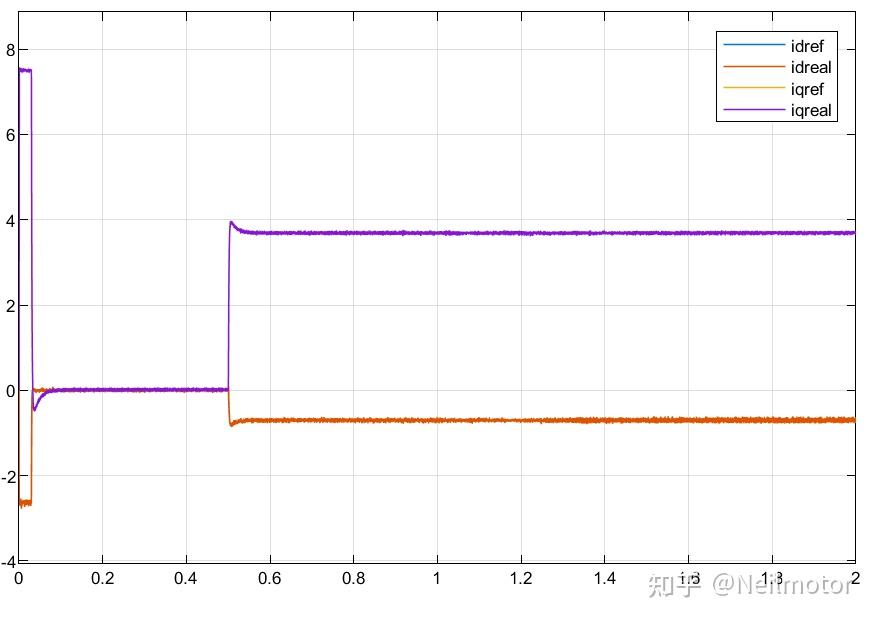
2.5dq轴给定电压
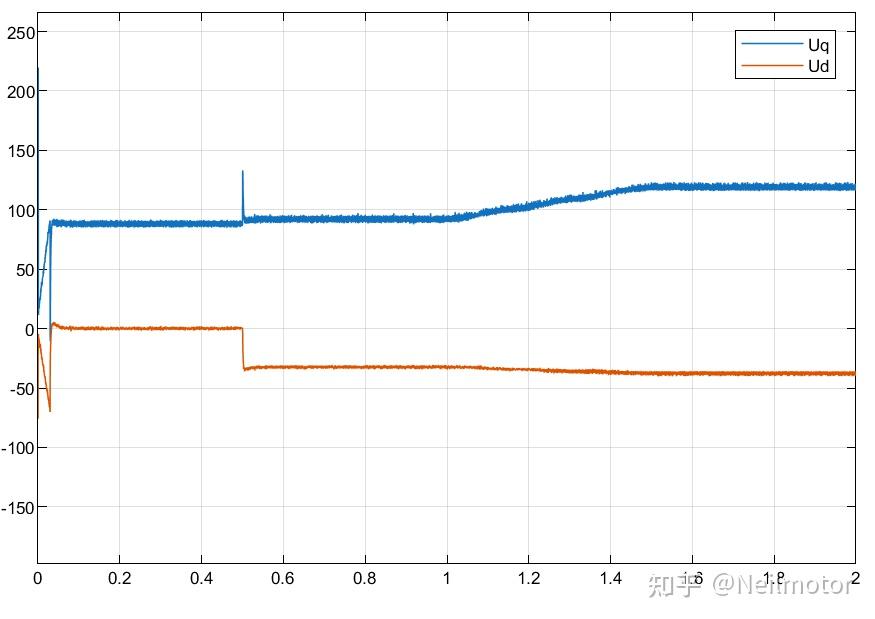
可以看出在输出电流保持不变的情况下,电机给定电压逐渐增加。
仿真工况3:电机空载零速启动,0s阶跃给定转速1000rpm,0.5s施加额定负载,1s时dq轴电感逐渐减小至0.5倍额定值,其他参数保持不变。
2.6dq轴电流
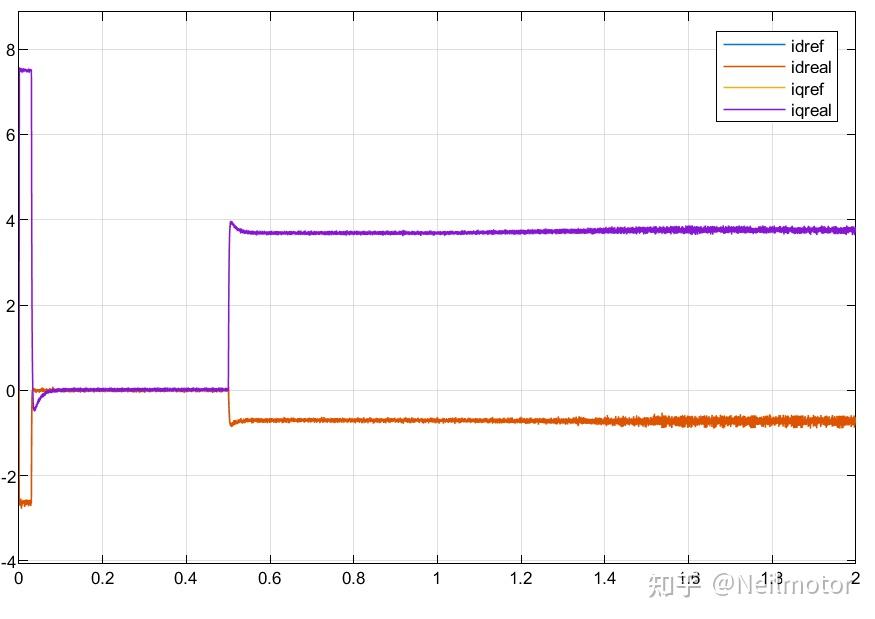
2.7dq轴给定电压
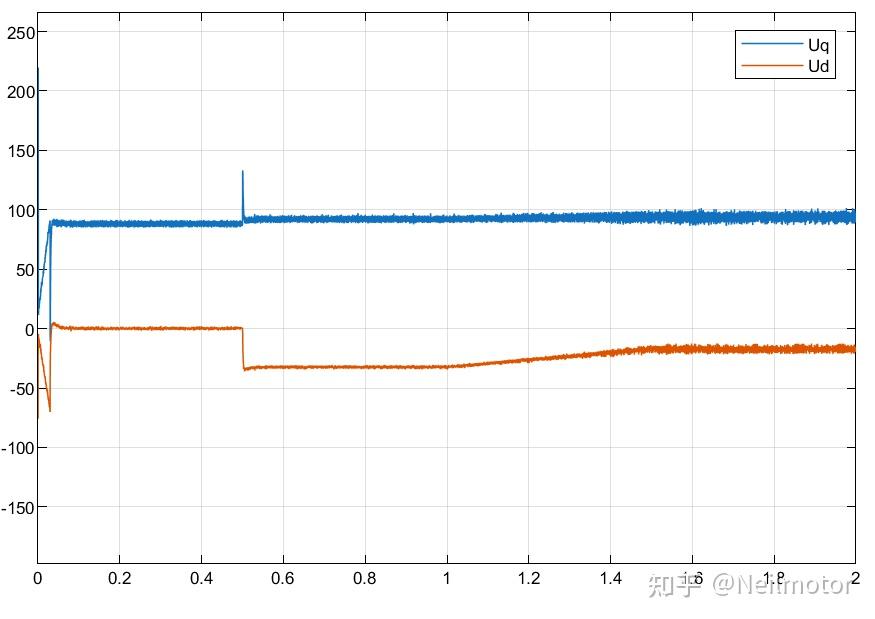
从上图可以看到,dq轴电流并未变化,这是由于采用直接公式法MTPA,电流分配依旧按照额定电流进行,但是由于dq轴电感发生变化,给定电压跟随发生变化。并且由于电感减小,电流波动变大。
仿真工况4:电机空载零速启动,0s阶跃给定转速1000rpm,0.5s施加额定负载,1s时转子磁链逐渐减小至0.5倍额定值,其他参数保持不变。
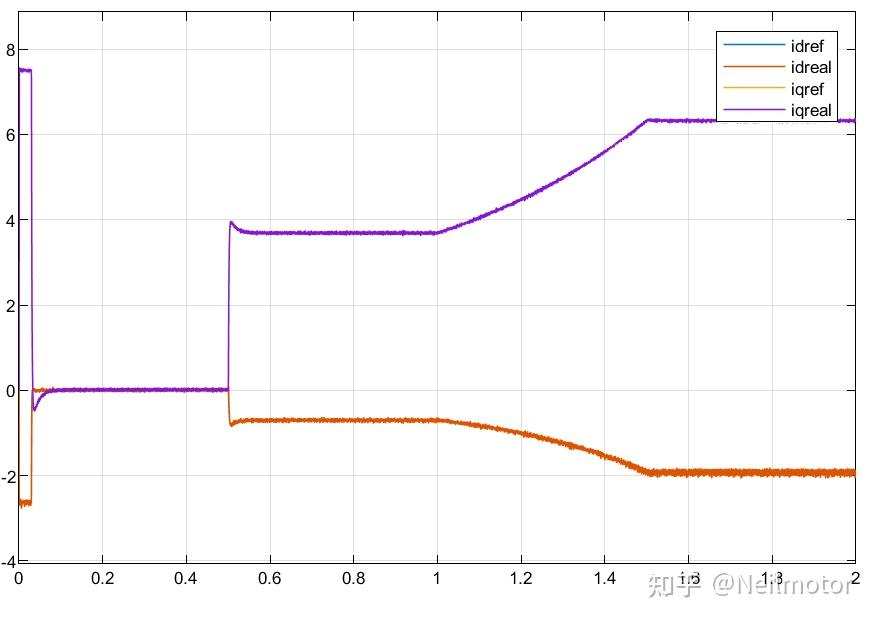
2.8dq轴电流
2.9dq轴给定电压
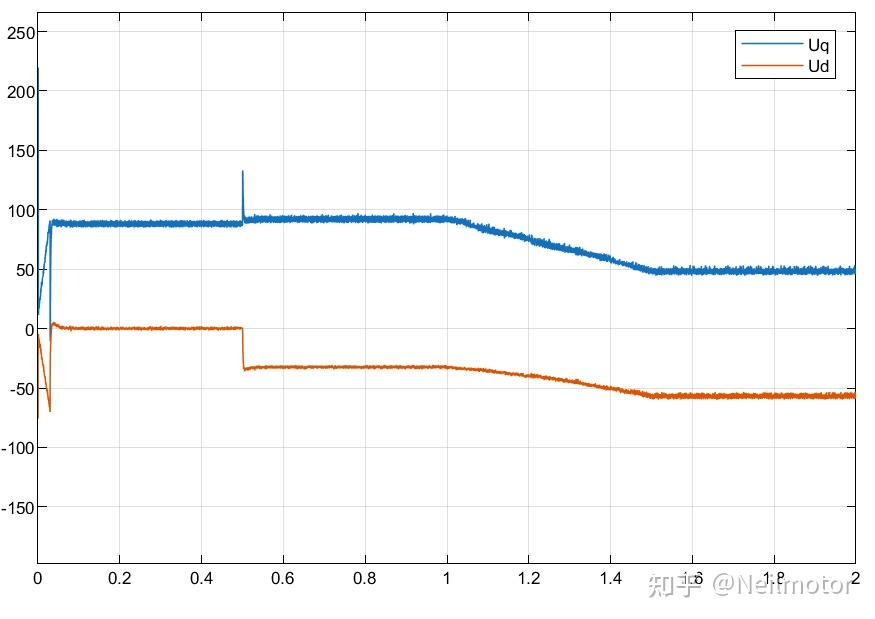
当电机磁链减小时,电机反电动势减小,所需电压也相应减小。根据电机电磁转矩公式,转子磁链减小时,如果要维持输出同样转矩,则需要增大电流。可以看出电压电流波形与理论分析基本一致。