目录
- [0 专栏介绍](#0 专栏介绍)
- [1 近端策略优化](#1 近端策略优化)
- [2 基于PPO算法的路径跟踪](#2 基于PPO算法的路径跟踪)
-
- [2.1 PPO网络设计](#2.1 PPO网络设计)
- [2.2 动作空间设计](#2.2 动作空间设计)
- [2.3 奖励函数设计](#2.3 奖励函数设计)
- [3 算法仿真](#3 算法仿真)
0 专栏介绍
本专栏以贝尔曼最优方程等数学原理为根基,结合PyTorch框架逐层拆解DRL的核心算法(如DQN、PPO、SAC)逻辑。针对机器人运动规划场景,深入探讨如何将DRL与路径规划、动态避障等任务结合,包含仿真环境搭建、状态空间设计、奖励函数工程化调优等技术细节,旨在帮助读者掌握深度强化学习技术在机器人运动规划中的实战应用
1 近端策略优化
在深度强化学习 | 详解从信赖域策略优化(TRPO)到近端策略优化(PPO)算法原理中,我们介绍了**近端策略优化(Proximal Policy Optimization, PPO)**算法,它是OpenAI推荐的首选深度强化学习算法之一。PPO算法的目标函数为
θ k + 1 = a r g max θ k + 1 J ( θ k + 1 ) \boldsymbol{\theta }{k+1}=\mathrm{arg}\max {\boldsymbol{\theta }{k+1}}J\left( \boldsymbol{\theta }{k+1} \right) θk+1=argθk+1maxJ(θk+1)
其中
J ( θ k + 1 ) = E ( s , a ) π θ k [ min ( π θ k + 1 ( s , a ) π θ k ( s , a ) A π θ k ( s , a ) , c l i p ( π θ k + 1 ( s , a ) π θ k ( s , a ) , 1 − ϵ , 1 + ϵ ) A π θ k ( s , a ) ) ] J\left( \boldsymbol{\theta }_{k+1} \right) =\mathbb{E} _{\left( \boldsymbol{s},\boldsymbol{a} \right) ~\pi _{\boldsymbol{\theta }_k}}\left[ \min \left( \frac{\pi {\boldsymbol{\theta }{k+1}}\left( \boldsymbol{s},\boldsymbol{a} \right)}{\pi _{\boldsymbol{\theta }_k}\left( \boldsymbol{s},\boldsymbol{a} \right)}A^{\pi _{\boldsymbol{\theta }_k}}\left( \boldsymbol{s},\boldsymbol{a} \right) , \mathrm{clip}\left( \frac{\pi {\boldsymbol{\theta }{k+1}}\left( \boldsymbol{s},\boldsymbol{a} \right)}{\pi _{\boldsymbol{\theta }_k}\left( \boldsymbol{s},\boldsymbol{a} \right)},1-\epsilon ,1+\epsilon \right) A^{\pi _{\boldsymbol{\theta }_k}}\left( \boldsymbol{s},\boldsymbol{a} \right) \right) \right] J(θk+1)=E(s,a) πθk[min(πθk(s,a)πθk+1(s,a)Aπθk(s,a),clip(πθk(s,a)πθk+1(s,a),1−ϵ,1+ϵ)Aπθk(s,a))]
PPO截断函数(PPO-Clip)
c l i p ( x , l , r ) \mathrm{clip}\left( x,l,r \right) clip(x,l,r)
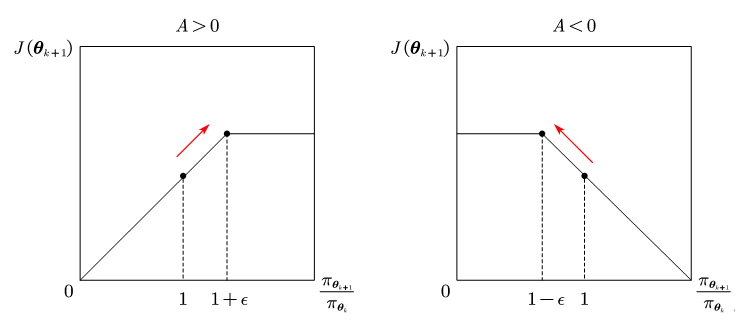
将 x x x限制在 [ l , r ] [l, r] [l,r]区间内。如图所示
- 若 A π θ k > 0 A^{\pi _{\boldsymbol{\theta }k}}>0 Aπθk>0说明该动作的价值高于平均,最大化 J ( θ k + 1 ) J\left( \boldsymbol{\theta }{k+1} \right) J(θk+1)需要增大 π θ k + 1 / π θ k {{\pi {\boldsymbol{\theta }{k+1}}}/{\pi _{\boldsymbol{\theta }_k}}} πθk+1/πθk,但不会让其超过 1 + ϵ 1+\epsilon 1+ϵ;
- 若 A π θ k < 0 A^{\pi _{\boldsymbol{\theta }k}}<0 Aπθk<0则最大化 J ( θ k + 1 ) J\left( \boldsymbol{\theta }{k+1} \right) J(θk+1)需要减小 π θ k + 1 / π θ k {{\pi {\boldsymbol{\theta }{k+1}}}/{\pi _{\boldsymbol{\theta }_k}}} πθk+1/πθk,但不会让其超过 1 − ϵ 1-\epsilon 1−ϵ
如下所示为PPO算法流程。

2 基于PPO算法的路径跟踪
2.1 PPO网络设计
PPO网络采用分层特征提取架构,其中共享特征提取器通过两层全连接网络(64→128单元)将原始观测映射为128维特征向量,为策略决策提供统一的潜在空间表示。策略网络在此特征基础上通过独立的双层MLP结构(64→32单元)输出动作分布,其对数标准差初始化为0.5以平衡探索与利用;价值评估网络则采用对称的双层MLP(64→32单元)结构,与策略网络共享特征提取器但保持独立的决策头,通过差异化网络参数实现特征表达的多样性,虽未显式配置双Q网络架构,但通过特征共享与独立处理的方式在PPO框架下实现了策略与价值函数的协同优化。下面为网络配置:
yaml
policy:
log_std_init: 0.5
feature_extractor:
mlp_dims: !!python/list [64, 128]
feature_dim: 128
actor_critic:
actor_dims: !!python/list [64, 32]
critic_dims: !!python/list [64, 32]2.2 动作空间设计
针对连续动作空间的特性设计了基于高斯分布采样的策略优化框架,以线速度 v v v和角速度 ω \omega ω为控制维度,构建了对称的二维连续动作空间 [ v , ω ] ∈ [ − v max , v max ] × [ − ω max , ω max ] \left[ v,\omega \right] \in \left[ -v_{\max},v_{\max} \right] \times \left[ -\omega _{\max},\omega _{\max} \right] [v,ω]∈[−vmax,vmax]×[−ωmax,ωmax]该设计通过上下界约束限定了动作输出的物理可行域,既避免因动作幅值过大导致运动失稳,又为策略网络的探索提供了明确的边界条件。进一步,通过高斯分布 N ( μ , σ ) \mathcal{N} \left( \mu ,\sigma \right) N(μ,σ)采样生成随机动作,再经tanh函数压缩至[-1,1]后线性映射到实际动作范围,既保证梯度可导性又满足动作边界约束。下面为动作配置
yaml
min_v: 0.0
max_v: 1.0
min_w: -2.0
max_w: 2.0
min_v_inc: -1.0
max_v_inc: 1.0
min_w_inc: -1.0
max_w_inc: 1.02.3 奖励函数设计
奖励函数设计采用多目标联合优化的混合奖励机制,通过时间惩罚、距离引导、目标达成奖励与碰撞惩罚的线性组合,构建了兼具探索激励与安全约束的强化学习回报,核心公式为:
R = r t i m e + α ( d t − 1 − d t ) + r r e a c h I w i n + r c o l l i s i o n I d e a d R=r_{\mathrm{time}}+\alpha \left( d_{t-1}-d_t \right) +r_{\mathrm{reach}}\mathbb{I} {\mathrm{win}}+r{\mathrm{collision}}\mathbb{I} _{\mathrm{dead}} R=rtime+α(dt−1−dt)+rreachIwin+rcollisionIdead
其中 d t d_t dt表示时刻 t t t智能体与目标的欧氏距离, I \mathbb{I} I为事件指示函数。时间惩罚项 r t i m e r_{\mathrm{time}} rtime作为基底奖励,通过固定负值施加步长成本压力,抑制智能体在环境中无效徘徊,驱动策略向高效路径收敛。距离引导项 α ( d t − 1 − d t ) \alpha \left( d_{t-1}-d_t \right) α(dt−1−dt)引入相对运动奖励机制,其中 α \alpha α为距离奖励系数,当智能体向目标靠近时 d t − 1 > d t d_{t-1}>d_t dt−1>dt产生正向激励,远离时 d t − 1 < d t d_{t-1}<d_t dt−1<dt施加负向惩罚,形成连续梯度信号引导策略优化方向。该设计相比绝对距离奖励更能话应动态环境,避免目标移动导致的奖励稀疏问题。目标达成奖励 r r e a c h r_{\mathrm{reach}} rreach作为稀疏奖励信号,仅在智能体进入目标区域时触发,通过显著的正向激励建立策略优化的全局目标导向。碰撞惩罚项 r c o l l i s i o n r_{\mathrm{collision}} rcollision则作为安全约束机制,当检测到与环境障碍物发生碰撞时施加高额负奖励,迫使策略学习规避高风险区域。
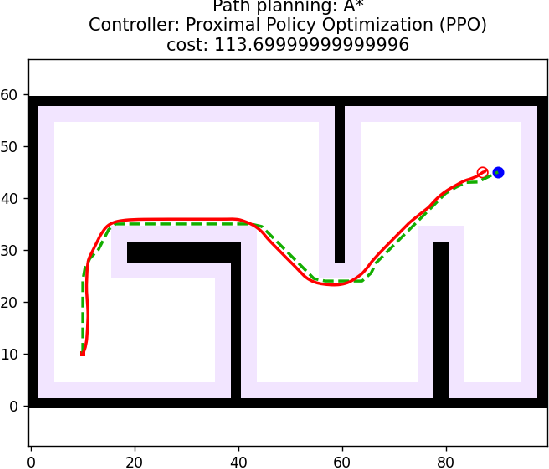
3 算法仿真
算法核心控制逻辑如下所示:
py
def plan(self, path: list):
lookahead_pts, lidar_frames_vis = [], []
self.start, self.goal = path[0], path[-1]
self.robot = DiffRobot(self.start.x(), self.start.y(), self.start.theta(), 0, 0)
dt = self.params["time_step"]
for _ in range(self.params["max_iteration"]):
# break until goal reached
robot_pose = Point3d(self.robot.px, self.robot.py, self.robot.theta)
if self.shouldRotateToGoal(robot_pose, self.goal):
real_path = np.array(self.robot.history_pose)[:, 0:2]
cost = np.sum(np.sqrt(np.sum(np.diff(real_path, axis=0) ** 2, axis=1, keepdims=True)))
LOG.INFO(f"{str(self)} Controller Controlling Successfully!")
# get the particular point on the path at the lookahead distance
lookahead_pt, _ = self.getLookaheadPoint(path)
lookahead_pts.append(lookahead_pt)
# update simulated lidar
states = np.array([[self.robot.px, self.robot.py, self.robot.theta]])
self.lidar.updateScans(states, self.obstacle_indices, self.map2index_func
# calculate velocity command
e_theta = self.regularizeAngle(self.robot.theta - self.goal[2]) / 10
if self.shouldRotateToGoal(robot_pose, self.goal):
if not self.shouldRotateToPath(abs(e_theta)):
u = DiffCmd(0, 0)
else:
u = DiffCmd(0, self.angularRegularization(e_theta / dt))
else:
e_theta = self.regularizeAngle(self.angle(robot_pose, lookahead_pt) - self.robot.theta)
if self.shouldRotateToPath(abs(e_theta), np.pi / 4):
u = DiffCmd(0, self.angularRegularization(e_theta / dt / 10))
else:
u = self.DDPGControl(robot_pose, lookahead_pt)
# feed into robotic kinematic
self.robot.kinematic(u, dt)
LOG.WARN(f"{str(self)} Controller Controlling Failed!")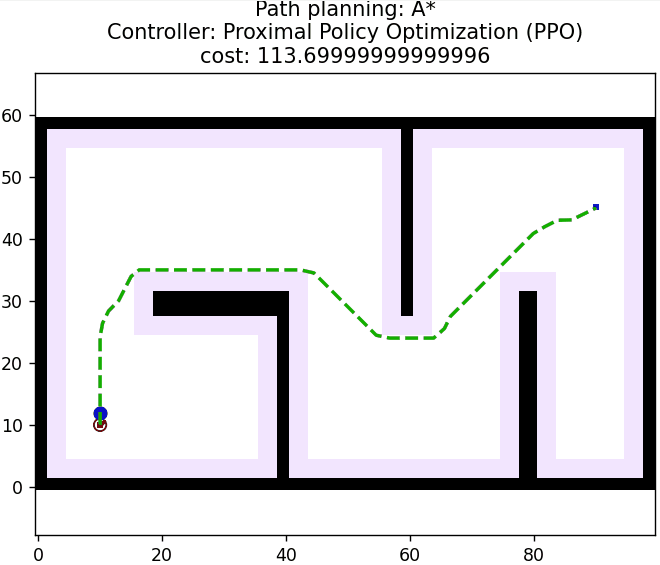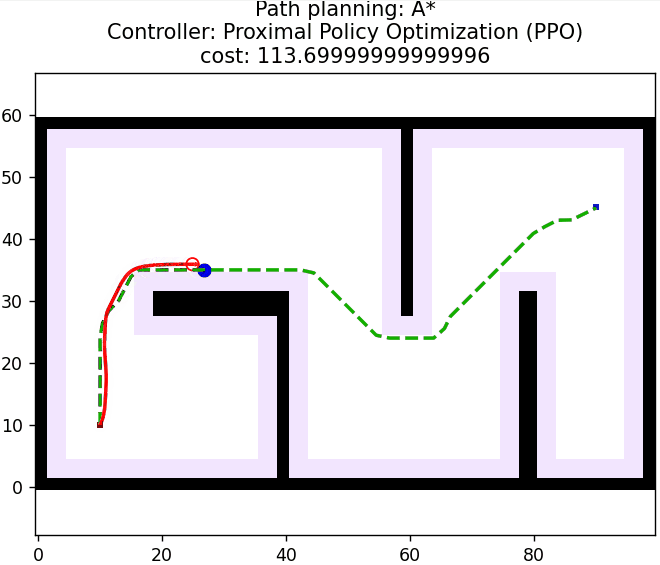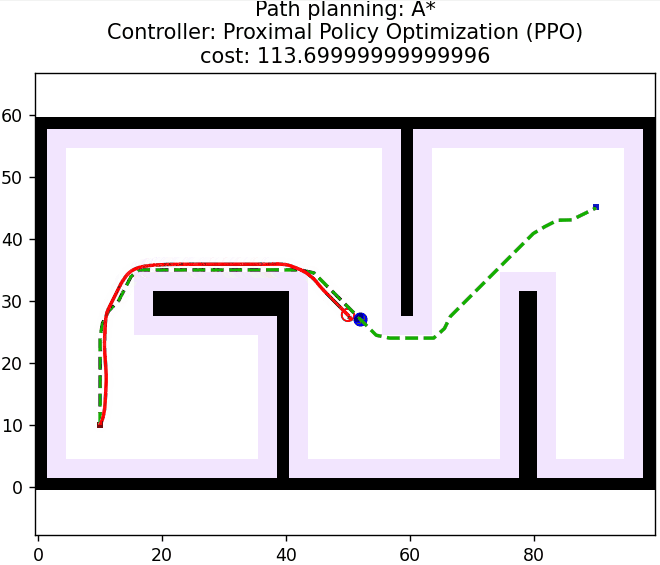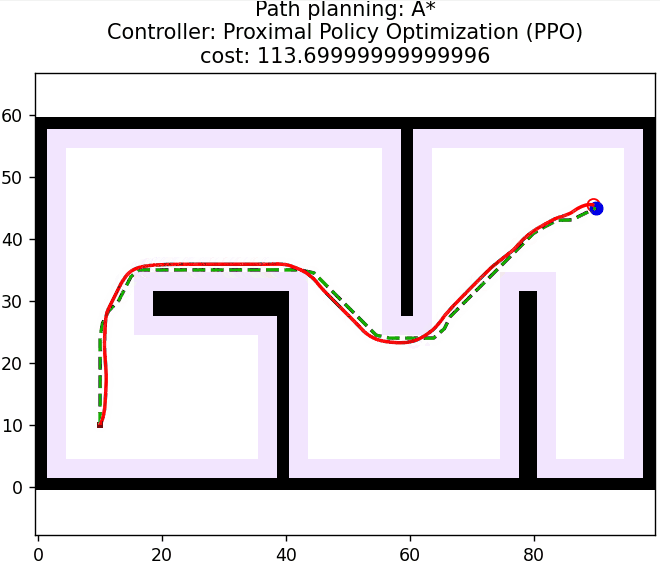
🔥 更多精彩专栏:
👇源码获取 · 技术交流 · 抱团学习 · 咨询分享 请联系👇