GS-RF网格搜索优化随机森林回归+SHAP分析+交叉验证+特征依赖图，MATLAB代码

一、主要功能

实现基于随机森林回归模型（Random Forest Regression） 的预测建模与参数优化流程，包括：

数据预处理与划分
网格搜索+交叉验证 优化模型参数
模型训练与评估
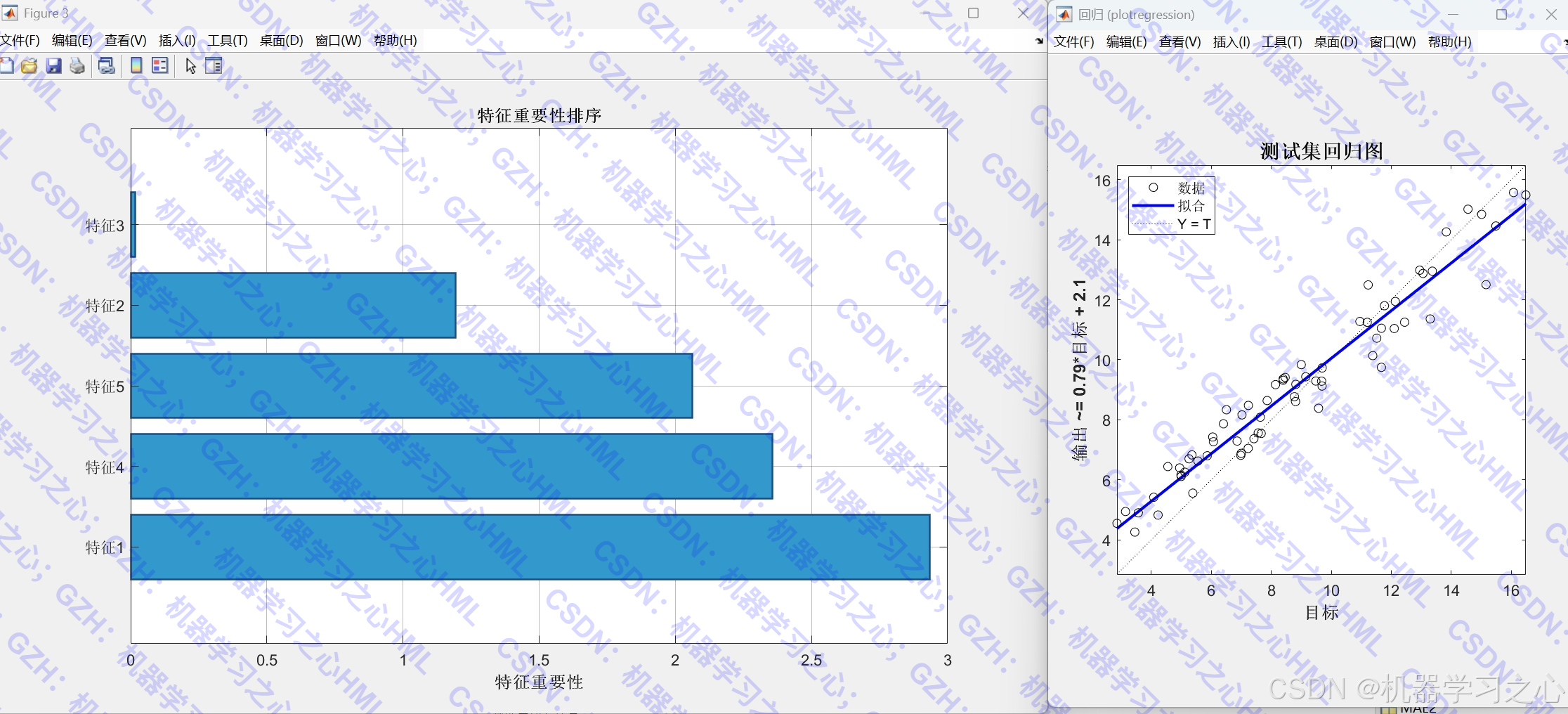
SHAP值分析 解释特征重要性
多维度可视化（参数搜索、误差曲线、拟合图、特征重要性等）

二、算法步骤

数据准备
- 读取Excel数据
- 随机打乱数据
- 划分训练集/测试集（7:3）
- 数据归一化（mapminmax）
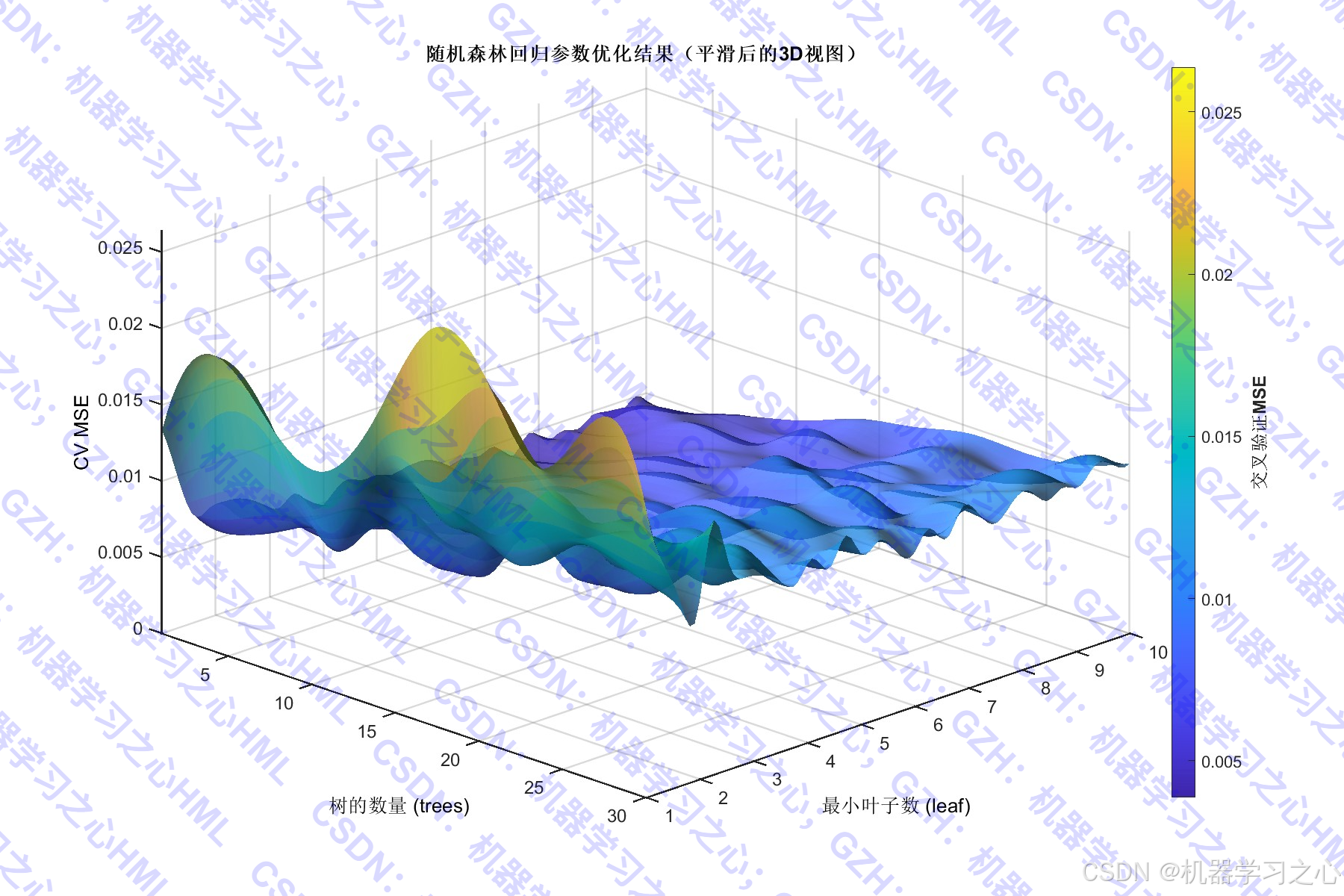
参数优化（网格搜索 + 5折交叉验证）
- 遍历 trees = 1:30
- 遍历 leaf = 1:10
- 计算每个参数组合的平均交叉验证MSE
模型训练
- 使用最优参数训练随机森林模型
- 计算袋外误差（OOB Error）
- 计算特征重要性
预测与评估
- 训练集/测试集预测
- 反归一化还原结果
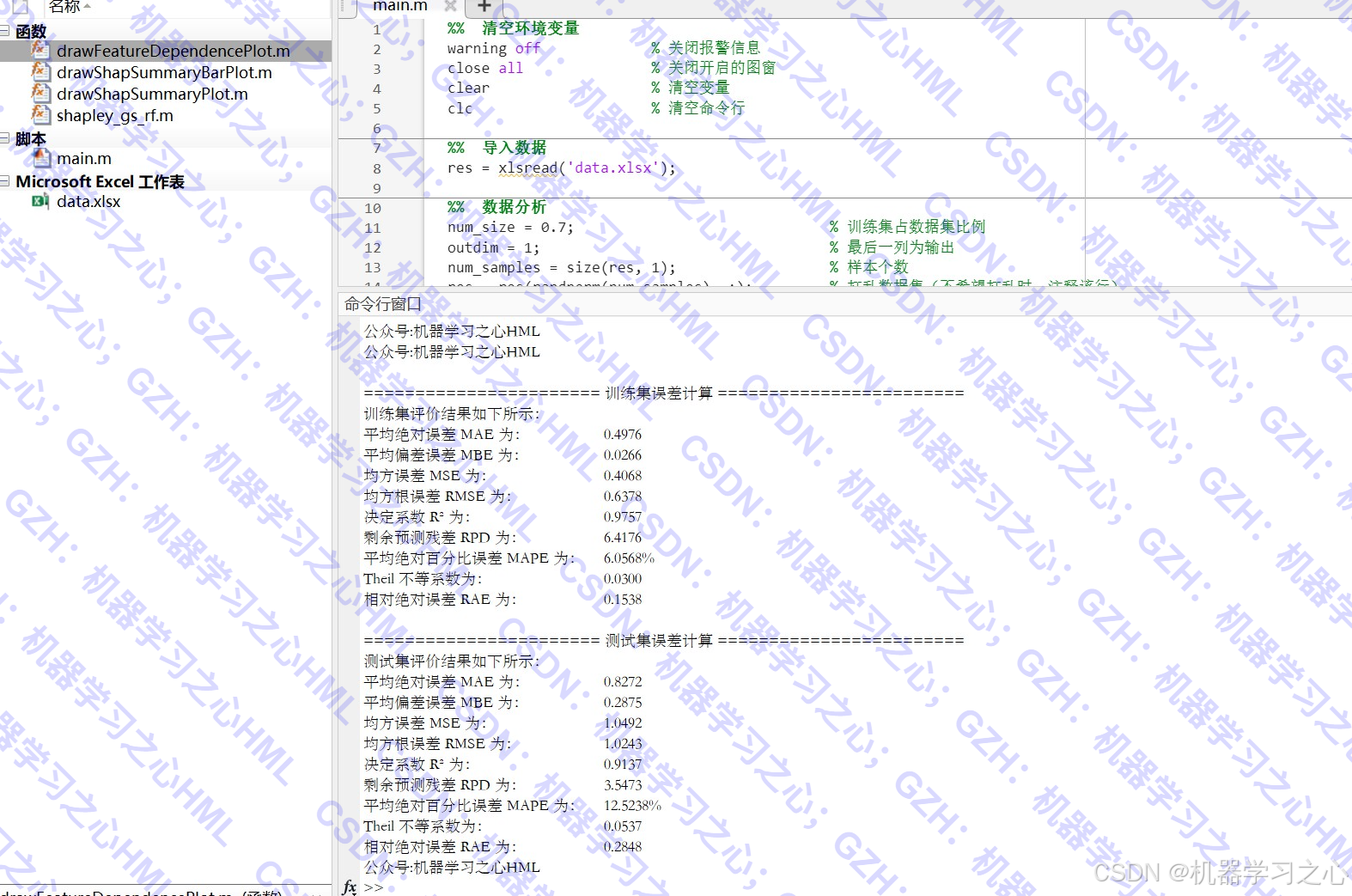
- 计算多个评估指标
SHAP分析
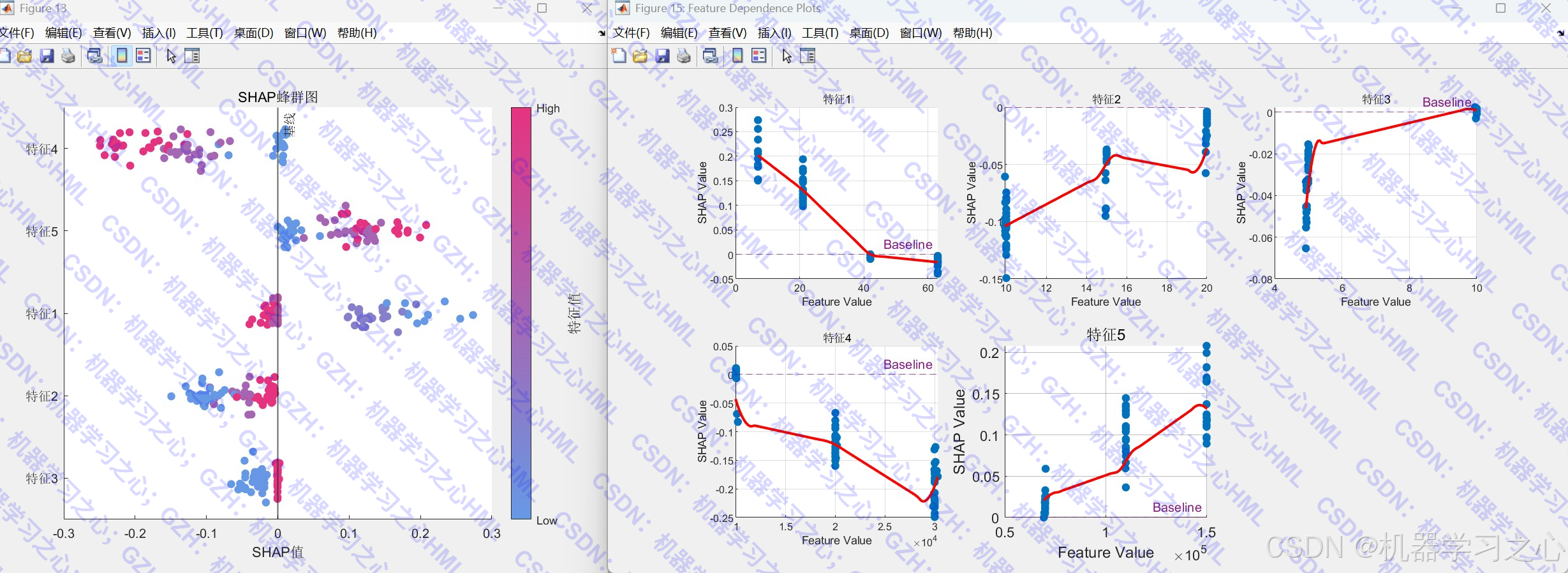
- 计算SHAP值解释特征贡献
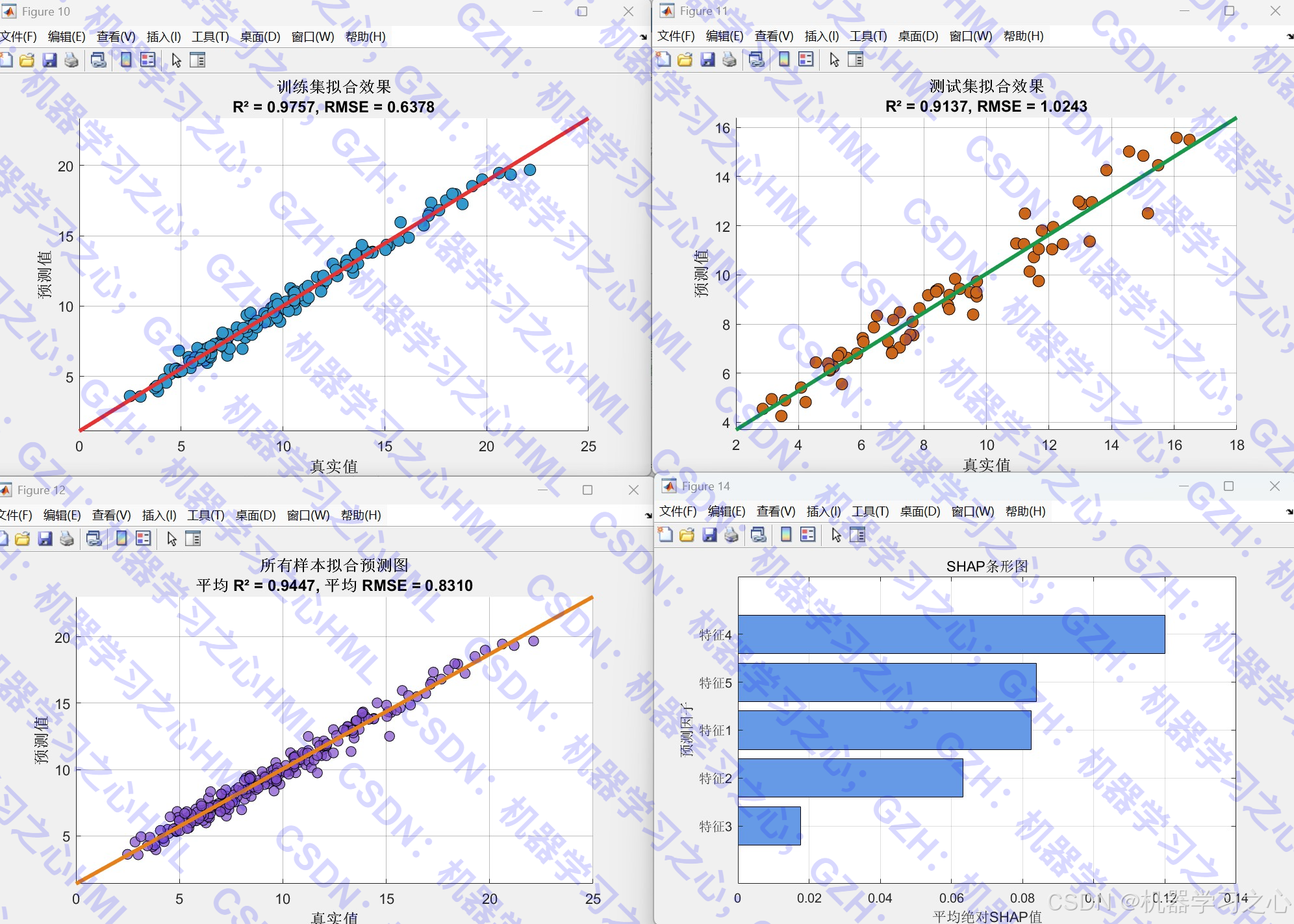
- 可视化SHAP摘要图与特征依赖图
可视化输出
- 参数搜索3D图
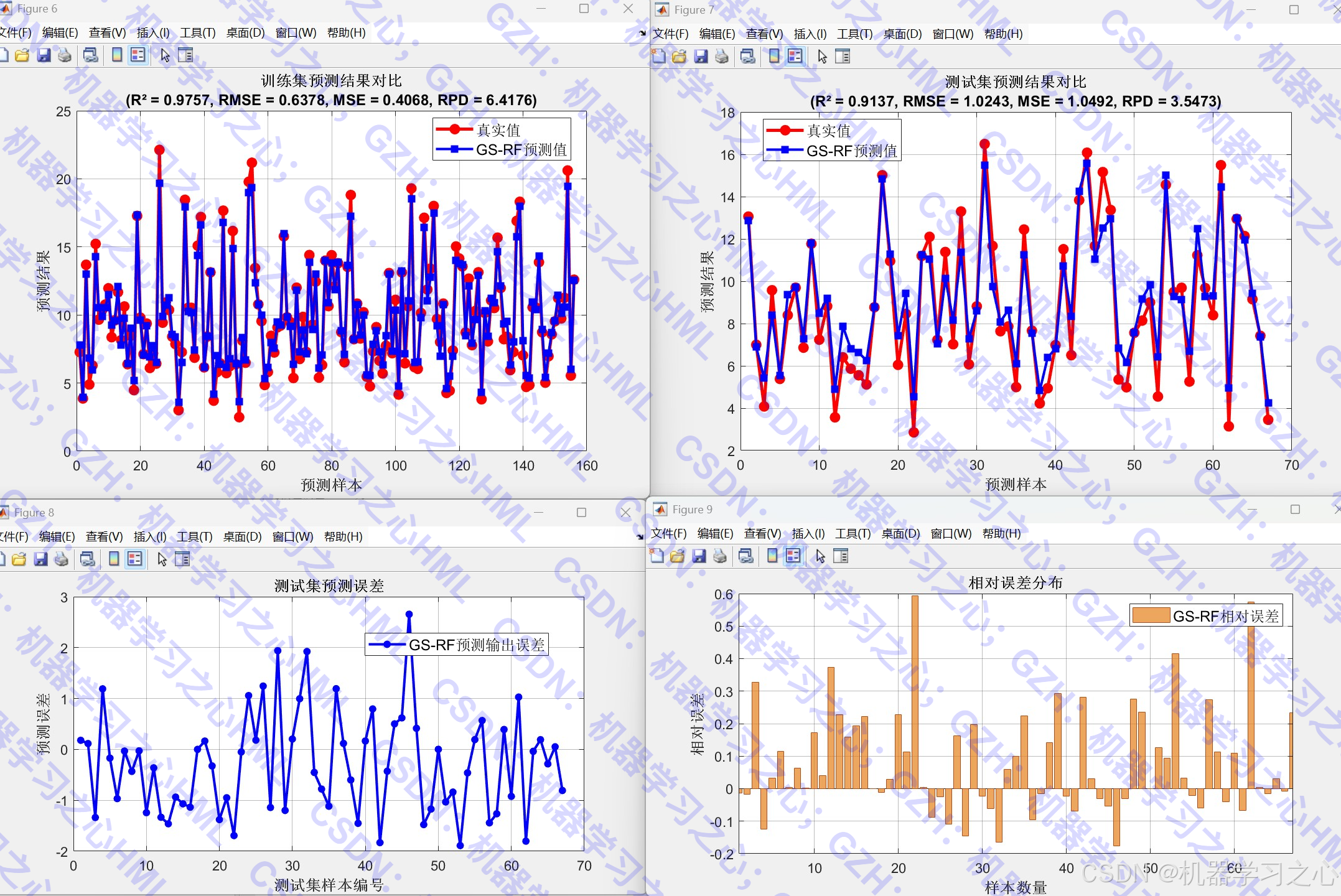
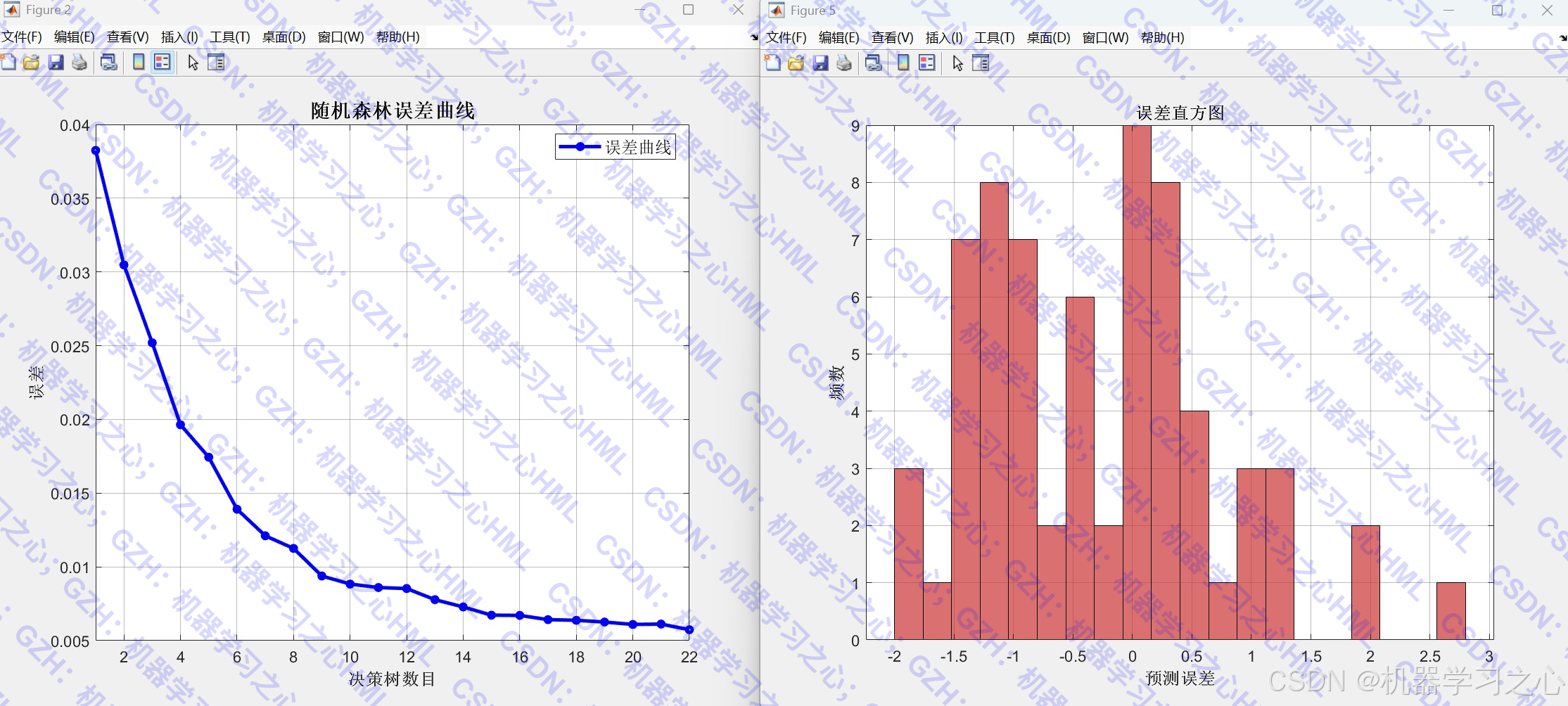
- 误差曲线、拟合图、误差直方图
- 特征重要性条形图
- 线性拟合散点图

三、技术路线

复制代码

数据导入 → 预处理 → 网格搜索+CV → 训练模型 → 预测 → 评估 → SHAP解释

模型：TreeBagger（MATLAB随机森林实现）
优化方法：网格搜索 + 5折交叉验证
解释方法：SHAP（Shapley Additive exPlanations）
评估指标：R²、RMSE、MAE、MAPE、RPD、Theil系数等

四、公式原理

1. 随机森林回归

多个决策树投票/平均输出
袋外误差（OOB Error）用于评估模型稳定性

2. 评估指标公式

RMSE ：
RMSE=1N∑(yi−y^i)2 RMSE = \sqrt{\frac{1}{N} \sum (y_i - \hat{y}_i)^2} RMSE=N1∑(yi−y^i)2
R² ：
R2=1−∑(yi−y^i)2∑(yi−yˉ)2 R^2 = 1 - \frac{\sum (y_i - \hat{y}_i)^2}{\sum (y_i - \bar{y})^2} R2=1−∑(yi−yˉ)2∑(yi−y^i)2
MAPE ：
MAPE=100%N∑∣yi−y^iyi∣ MAPE = \frac{100\%}{N} \sum \left| \frac{y_i - \hat{y}_i}{y_i} \right| MAPE=N100%∑ yiyi−y^i
Theil系数 ：
U=1N∑(yi−y^i)21N∑yi2+1N∑y^i2 U = \frac{\sqrt{\frac{1}{N} \sum (y_i - \hat{y}_i)^2}}{\sqrt{\frac{1}{N} \sum y_i^2} + \sqrt{\frac{1}{N} \sum \hat{y}_i^2}} U=N1∑yi2 +N1∑y^i2 N1∑(yi−y^i)2

3. SHAP值

基于合作博弈论，计算每个特征对预测的边际贡献：

ϕi=∑S⊆F∖{i}∣S∣!(∣F∣−∣S∣−1)!∣F∣![f(S∪{i})−f(S)] \phi_i = \sum_{S \subseteq F \setminus \{i\}} \frac{|S|!(|F|-|S|-1)!}{|F|!} [f(S \cup \{i\}) - f(S)] ϕi=S⊆F∖{i}∑∣F∣!∣S∣!(∣F∣−∣S∣−1)![f(S∪{i})−f(S)]

五、参数设定

参数	取值/范围	说明
`num_size`	0.7	训练集比例
`trees_range`	1:30	决策树数量搜索范围
`leaf_range`	1:10	最小叶子样本数搜索范围
`k`（折数）	5	交叉验证折数
`Method`	'regression'	回归任务

六、运行环境

平台：MATLAB R2018b 或更高版本
必要工具箱 ：
- Statistics and Machine Learning Toolbox
- 可能需要 SHAP 自定义函数支持
数据格式：Excel文件（.xlsx），最后一列为输出变量

七、应用场景

适用于回归预测问题，如：

房价预测
销量/需求预测
工业过程参数预测
环境因子影响分析
金融风险评估

特别适合：

中小规模数据集
特征间存在复杂非线性关系
需要模型解释（SHAP）的场景