正则化全面解析：从过拟合防治到模型优化之道

文章目录

- [1. 引言](#1. 引言)
- - [1.1 问题定义：机器学习和深度学习中的"过拟合"克星](#1.1 问题定义：机器学习和深度学习中的"过拟合"克星)
  - [1.2 为什么叫"正则化"？术语的由来与含义](#1.2 为什么叫"正则化"？术语的由来与含义)
  - - [🔢 数学起源：化"不适定"为"适定"](#🔢 数学起源：化“不适定”为“适定”)
    - [📖 词义对应："正"其"规"则](#📖 词义对应：“正”其“规”则)
    - [🎯 技术目标：立"规矩"成"典范"](#🎯 技术目标：立“规矩”成“典范”)
    - [📊 核心要义总结](#📊 核心要义总结)
- [2. 核心思想：约束引导泛化](#2. 核心思想：约束引导泛化)
- - [2.1 奥卡姆剃刀原理](#2.1 奥卡姆剃刀原理)
  - [2.2 优化理论角度：约束优化问题](#2.2 优化理论角度：约束优化问题)
  - [2.3 贝叶斯角度：最大后验概率估计（MAP）](#2.3 贝叶斯角度：最大后验概率估计（MAP）)
  - [2.4 偏差-方差权衡角度](#2.4 偏差-方差权衡角度)
- [3. 数学原理：第一性原理解读](#3. 数学原理：第一性原理解读)
- - [3.1 基本数学框架](#3.1 基本数学框架)
  - [3.2 L1与L2正则化的数学本质](#3.2 L1与L2正则化的数学本质)
  - [3.3 几何解释](#3.3 几何解释)
- [4. 演进过程：正则化技术发展图谱](#4. 演进过程：正则化技术发展图谱)
- [5. 关键步骤：实现正则化的通用流程](#5. 关键步骤：实现正则化的通用流程)
- [6. 举例说明：房价预测案例](#6. 举例说明：房价预测案例)
- [7. 总结](#7. 总结)
- - [7.1 优缺点与应用场景对比](#7.1 优缺点与应用场景对比)
  - [7.2 选择指南与实践建议](#7.2 选择指南与实践建议)

1. 引言

1.1 问题定义：机器学习和深度学习中的"过拟合"克星

在机器学习和深度学习中，我们常常面临一个核心挑战：模型在训练数据上表现卓越，但在未见过的测试数据或新数据上表现不佳。这种现象被称为过拟合。这就好比一个学生通过死记硬背习题答案在随堂测验中得了高分，却在考察综合理解能力的期末考试中失利。

正则化技术正是为了解决这一问题而生的。

输入：原始的模型训练过程，主要包括原始损失函数 （如均方误差、交叉熵）和训练数据
输出：一个经过修改的、新的优化目标 。这个新目标在原始损失函数的基础上，增加了一个额外的正则化项，用于惩罚模型的复杂度，从而引导模型选择更简单、泛化能力更强的解

过拟合的本质是模型复杂度过高，过度"学习"了训练数据中的噪声和无关细节，而非数据背后的普遍规律。正则化通过引入额外的约束，在"拟合训练数据"和"保持模型简单"之间寻求最佳平衡。

1.2 为什么叫"正则化"？术语的由来与含义

正则化（Regularization）这一名称的由来，可以从三个紧密关联的层面理解，它精准地概括了该技术的核心思想与目标。

🔢 数学起源：化"不适定"为"适定"

正则化概念源于数学领域，用于解决不适定问题 ------这类问题可能解不唯一，或者解会随着数据的微小扰动而发生剧烈变化，这正是机器学习中过拟合 的数学本质。通过向目标函数添加一个惩罚项（即正则项），为解空间施加约束，从而将不适定问题转化为解唯一且稳定的适定问题 。这个数学上的"规范化"过程，被称为正则化。

📖 词义对应："正"其"规"则

中文翻译"正则化"非常传神地捕捉了英文"Regularization"的精髓。

"正" 有"纠正、规范"之意，对应了纠正模型过拟合这种"不正"的病态。
"则" 即"规则、法则"，对应了所添加的约束项 （如L1/L2范数）。
因此，"正则化"本质就是"通过引入规则，使模型参数或输出变得端正、规范"。

🎯 技术目标：立"规矩"成"典范"

从机器学习的实践角度看，正则化的目的是给模型的训练"立规矩"。没有正则化时，模型可能为追求极低的训练误差而"为所欲为"，导致过拟合。正则化通过约束模型复杂度 （如限制参数大小），引导模型在"拟合训练数据"和"保持模型简单"之间取得平衡，最终目标是获得泛化能力强的"规范"模型。

📊 核心要义总结

理解层面	核心要义	关键洞察
数学起源	通过增加约束，将不适定问题转化为适定问题。	使问题的解在数学上更稳定、更可靠。
中文词义	"正 "是纠正、规范；"则"是规则、法则。	名称直译了"通过引入规则使其规范化"的技术本质。
技术目标	给模型训练立下"规矩"，约束参数行为，防止过拟合。	目标是获得一个行为更"规范"、泛化能力更强的模型。

2. 核心思想：约束引导泛化

正则化的关键洞察非常巧妙：对模型复杂度施加适当的约束，反而能引导其学习到更本质、更通用的规律。这一思想源于几个重要的原理。

2.1 奥卡姆剃刀原理

"如无必要，勿增实体"。在多个能同样好地解释训练数据的模型中，更简单的模型通常具有更好的泛化能力。正则化是这一哲学思想在机器学习中的直接体现，它通过引入约束来避免模型过度复杂，从而提升其在新数据上的表现。

2.2 优化理论角度：约束优化问题

在机器学习中，训练神经网络本质上是解决一个优化问题：最小化损失函数 J ( θ ) J(\theta) J(θ)，其中 θ \theta θ 表示模型参数。如果没有正则化，目标是最小化经验风险（empirical risk）：

min ⁡ θ J ( θ ) = 1 n ∑ i = 1 n L ( y i , f ( x i ; θ ) ) \min_{\theta} J(\theta) = \frac{1}{n} \sum_{i=1}^{n} L(y_i, f(x_i; \theta)) θminJ(θ)=n1i=1∑nL(yi,f(xi;θ))

其中 L L L 是损失函数， n n n 是样本数。

然而，经验风险最小化容易导致过拟合，因为模型可能过度拟合训练数据中的噪声。正则化通过添加一个正则项 R ( θ ) R(\theta) R(θ) 来修改目标函数，形成结构风险最小化（structural risk minimization）：

min ⁡ θ J ( θ ) + λ R ( θ ) \min_{\theta} J(\theta) + \lambda R(\theta) θminJ(θ)+λR(θ)

其中 λ \lambda λ 是正则化强度超参数，控制惩罚的力度。

为什么添加正则项有效？ 从优化理论看，正则项相当于在参数空间中添加了一个约束，迫使参数值不能过大。例如，L2正则化对应约束 ∣ θ ∣ 2 2 ≤ c |\theta|_2^2 \leq c ∣θ∣22≤c，这限制了参数向量的欧几里得范数，使解更平滑。从数学上看，可以通过拉格朗日乘子法将原始约束优化问题转化为无约束问题，其中正则项是约束的软形式。

2.3 贝叶斯角度：最大后验概率估计（MAP）

从贝叶斯推断的角度看，正则化可以解释为最大后验概率估计（MAP）。假设参数 θ \theta θ 是一个随机变量，我们想根据数据 D D D 估计 θ \theta θ。贝叶斯定理为：

P ( θ ∣ D ) = P ( D ∣ θ ) P ( θ ) P ( D ) P(\theta | D) = \frac{P(D | \theta) P(\theta)}{P(D)} P(θ∣D)=P(D)P(D∣θ)P(θ)

其中：

P ( D ∣ θ ) P(D | \theta) P(D∣θ) 是似然函数，对应损失函数（如负对数似然）
P ( θ ) P(\theta) P(θ) 是先验分布，表示对参数的先验知识
P ( θ ∣ D ) P(\theta | D) P(θ∣D) 是后验分布

最大化后验概率（MAP）等价于最小化负对数后验：

− log ⁡ P ( θ ∣ D ) = − log ⁡ P ( D ∣ θ ) − log ⁡ P ( θ ) + 常数 -\log P(\theta | D) = -\log P(D | \theta) - \log P(\theta) + \text{常数} −logP(θ∣D)=−logP(D∣θ)−logP(θ)+常数

这类似于损失函数加正则项： J ( θ ) = − log ⁡ P ( D ∣ θ ) J(\theta) = -\log P(D | \theta) J(θ)=−logP(D∣θ) 是损失函数，而 R ( θ ) = − log ⁡ P ( θ ) R(\theta) = -\log P(\theta) R(θ)=−logP(θ) 是正则项。

L2正则化 ：对应高斯先验。假设 θ ∼ N ( 0 , σ 2 I ) \theta \sim \mathcal{N}(0, \sigma^2 I) θ∼N(0,σ2I)，则 − log ⁡ P ( θ ) ∝ ∣ θ ∣ 2 2 -\log P(\theta) \propto |\theta|_2^2 −logP(θ)∝∣θ∣22，即L2正则项
L1正则化 ：对应拉普拉斯先验。假设 θ ∼ Laplace ( 0 , b ) \theta \sim \text{Laplace}(0, b) θ∼Laplace(0,b)，则 − log ⁡ P ( θ ) ∝ ∣ θ ∣ 1 -\log P(\theta) \propto |\theta|_1 −logP(θ)∝∣θ∣1，即L1正则项

因此，正则化从贝叶斯视角引入了参数的先验分布，将领域知识或偏好融入估计过程。

2.4 偏差-方差权衡角度

从统计学习角度看，正则化通过偏差-方差权衡（bias-variance tradeoff）来改善泛化能力。模型的期望误差可以分解为：

误差 = 偏差 2 + 方差 + 噪声 \text{误差} = \text{偏差}^2 + \text{方差} + \text{噪声} 误差=偏差2+方差+噪声

偏差：模型预测与真实值的平均差异，表示模型本身的误差
方差：模型预测的波动程度，表示对训练数据变化的敏感性

没有正则化时，复杂模型可能具有低偏差但高方差（导致过拟合）。正则化通过惩罚较大的参数值，增加了模型的偏差（因为模型变得相对简单），但显著减少了方差，从而可能降低总误差。这解释了正则化如何平衡模型复杂度和拟合能力，最终提升泛化性能。

3. 数学原理：第一性原理解读

从第一性原理出发，正则化的数学本质可以通过优化理论和概率视角来解读。

3.1 基本数学框架

正则化通过修改目标函数实现，其通用形式为：

J regularized ( θ ) = J ( θ ) + λ R ( θ ) J_{\text{regularized}}(\theta) = J(\theta) + \lambda R(\theta) Jregularized(θ)=J(θ)+λR(θ)

其中：

J ( θ ) J(\theta) J(θ) 是原始损失函数
λ \lambda λ 是正则化系数，控制惩罚的强度
R ( θ ) R(\theta) R(θ) 是正则化项，是模型参数 θ \theta θ 的函数

3.2 L1与L2正则化的数学本质

L2正则化（权重衰减）：

正则化项： R ( θ ) = 1 2 ∣ θ ∣ 2 2 = 1 2 ∑ θ i 2 R(\theta) = \frac{1}{2} |\theta|_2^2 = \frac{1}{2} \sum \theta_i^2 R(θ)=21∣θ∣22=21∑θi2
梯度下降中的权重更新变为： θ t + 1 = ( 1 − η λ ) θ t − η ∇ J ( θ t ) \theta_{t+1} = (1-\eta \lambda) \theta_t - \eta \nabla J(\theta_t) θt+1=(1−ηλ)θt−η∇J(θt)
作用机制 ：在每一步更新时，权重会先乘以一个小于1的因子 ( 1 − η λ ) (1-\eta \lambda) (1−ηλ)，再进行正常的梯度下降。这会导致所有权重被均匀地收缩，趋向于较小值但一般不为零

L1正则化（Lasso）：

正则化项： R ( θ ) = ∣ θ ∣ 1 = ∑ ∣ θ i ∣ R(\theta) = |\theta|_1 = \sum |\theta_i| R(θ)=∣θ∣1=∑∣θi∣
梯度中包含符号函数： ∇ J L 1 ( θ ) ∝ ... + λ ⋅ sign ( θ ) \nabla J_{L1}(\theta) \propto \ldots + \lambda \cdot \text{sign}(\theta) ∇JL1(θ)∝...+λ⋅sign(θ)
作用机制 ：L1正则化对参数的惩罚是一个固定步长 （与权重值大小无关），方向始终指向零点。这使得较小的权重很容易被"推过"零点而直接变为零，从而产生稀疏解（部分权重精确为零）

3.3 几何解释

下图直观展示了L1和L2正则化如何通过约束区域影响最优解的位置：
原始损失函数等高线正则化约束区域 L1: 菱形 L2: 圆形最优解常出现在尖角
导致稀疏性最优解在光滑边界上
权重普遍缩小

L1的"尖角"与稀疏性：L1的约束区域是菱形（多维下为多面体），有"尖角"突出。最优解常出现在这些位于坐标轴上的尖角，导致部分权重恰好为0
L2的"平滑"与收缩性：L2的约束区域是圆形（多维下为球体），边界光滑。最优解使所有权重均匀变小，但很少精确为0

4. 演进过程：正则化技术发展图谱

正则化技术并非一成不变，它经历了一个从简单到复杂、从单一到多元的演进过程。

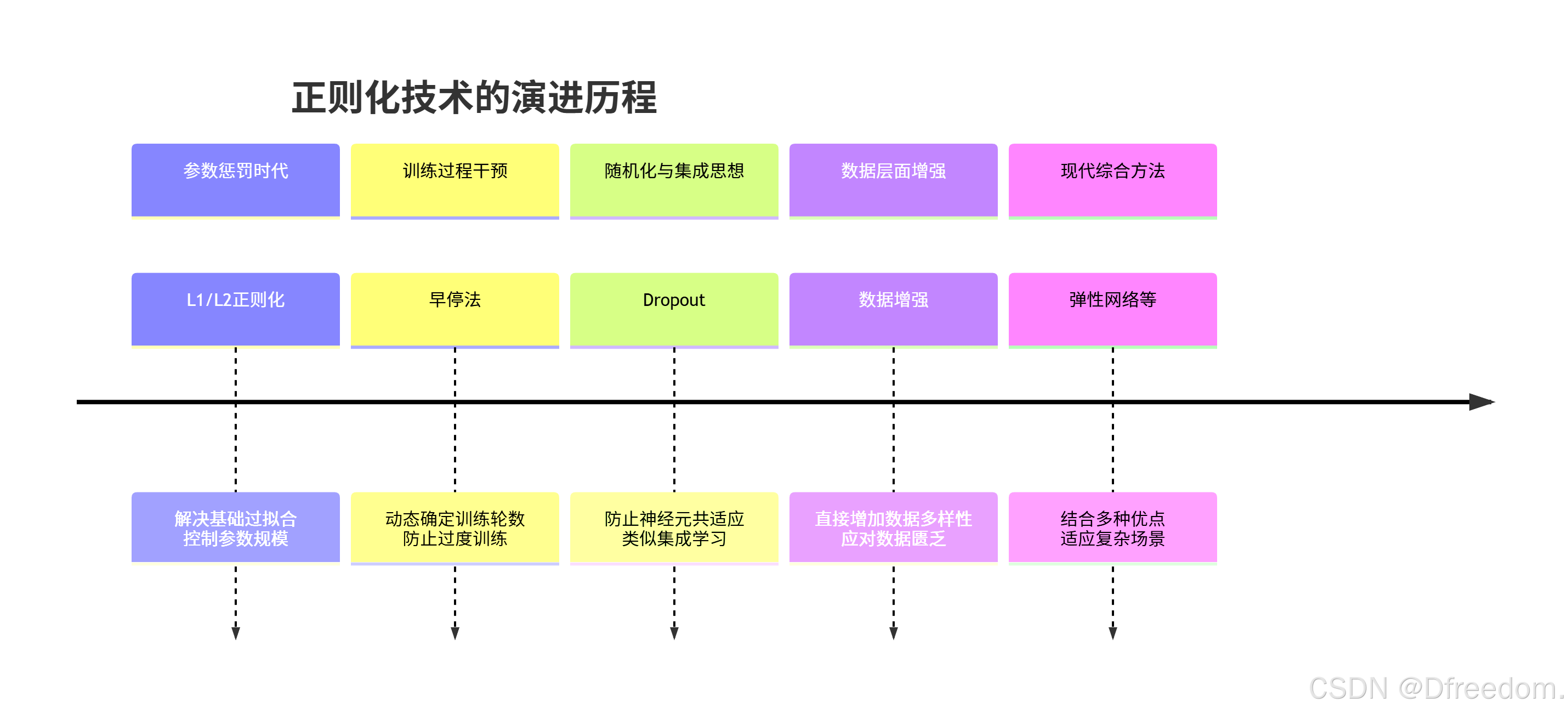
L1/L2正则化：最早且最基础的正则化方法，通过直接惩罚模型参数的大小来控制模型复杂度
早停法：一种简单高效的正则化策略，在模型开始过拟合前停止训练，无需修改损失函数
Dropout：深度学习中革命性的技术，通过随机"关闭"神经元防止网络过度依赖局部特征，类似集成学习
数据增强：通过在数据层面施加变换（如图像旋转、裁剪）来增加数据量和多样性，是一种非常有效的正则化方式
现代发展 ：出现了如弹性网络 （结合L1和L2）、批归一化（在稳定训练的同时带来正则化效果）等更复杂的方法

5. 关键步骤：实现正则化的通用流程

在实际项目中应用正则化，通常遵循一个系统化的流程：

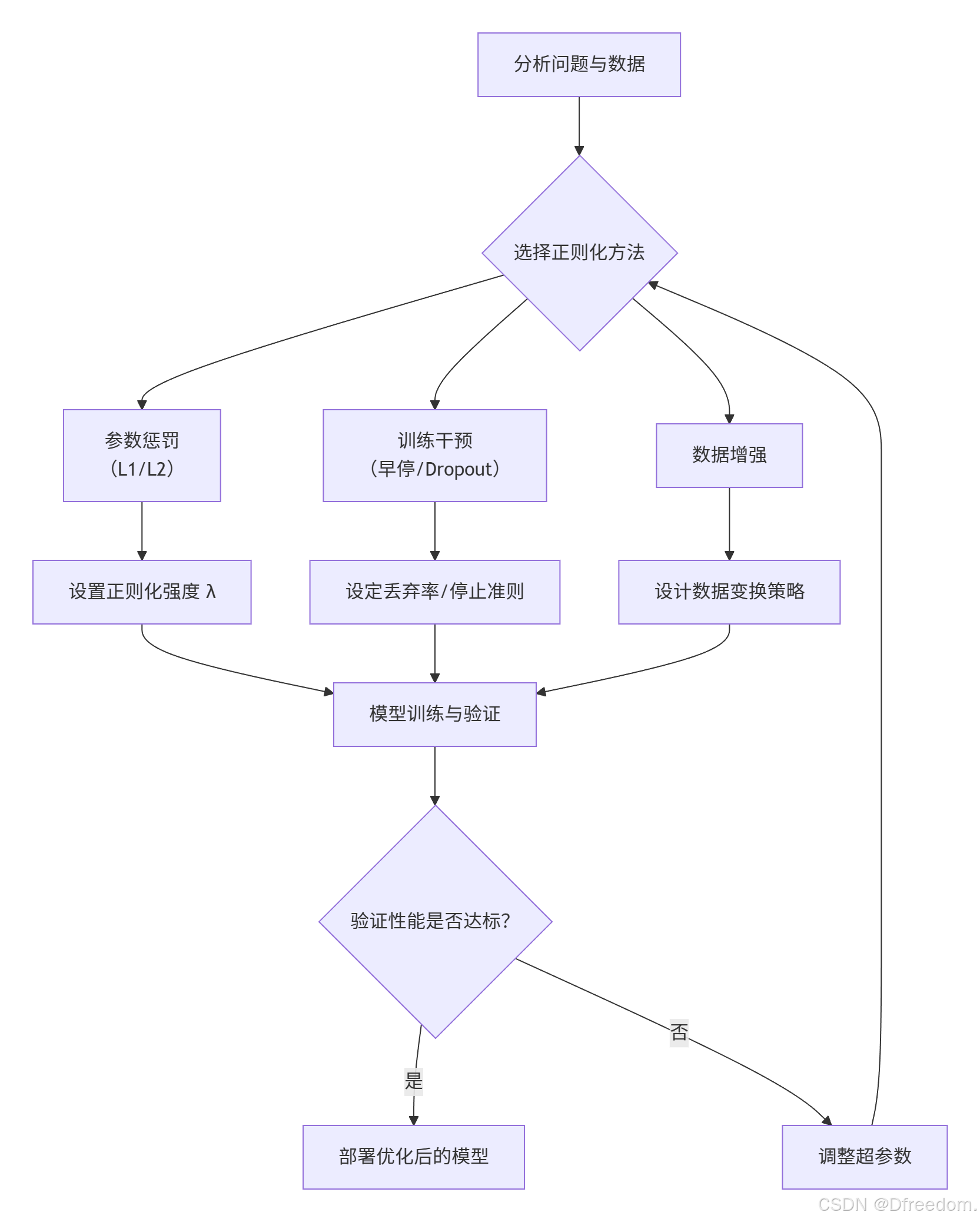
问题分析：明确过拟合风险程度、数据特征和模型复杂度
方法选择：根据具体需求选择合适的正则化技术
参数设置：确定正则化强度（λ）、Dropout比率、早停法的耐心值等超参数
模型训练与验证：使用修改后的目标函数或训练策略进行模型训练，并在验证集上评估性能
调优与部署：根据验证集性能调整超参数，循环迭代，直至模型达到最佳泛化能力，然后部署

6. 举例说明：房价预测案例

假设我们用一个线性模型预测房价，特征包括面积（ x 1 x_1 x1）、卧室数（ x 2 x_2 x2）、卫生间数（ x 3 x_3 x3）、房龄（ x 4 x_4 x4）。模型为 y = w 1 x 1 + w 2 x 2 + w 3 x 3 + w 4 x 4 + b y = w_1x_1 + w_2x_2 + w_3x_3 + w_4x_4 + b y=w1x1+w2x2+w3x3+w4x4+b。

无正则化的问题：模型可能给所有特征分配很大的权重（包括可能不重要的"房龄"），完美拟合训练数据中的噪声，导致在新房源数据上预测不准
应用L2正则化 ：
- 损失函数变为： J = MSE + λ ( w 1 2 + w 2 2 + w 3 2 + w 4 2 ) J = \text{MSE} + \lambda (w_1^2 + w_2^2 + w_3^2 + w_4^2) J=MSE+λ(w12+w22+w32+w42)
- 效果：所有权重被均匀缩小，模型变得更平滑稳定。房龄特征仍被保留，但影响力减弱。模型不再过度依赖任何单一特征，泛化能力提升
应用L1正则化 ：
- 损失函数变为： J = MSE + λ ( ∣ w 1 ∣ + ∣ w 2 ∣ + ∣ w 3 ∣ + ∣ w 4 ∣ ) J = \text{MSE} + \lambda (|w_1| + |w_2| + |w_3| + |w_4|) J=MSE+λ(∣w1∣+∣w2∣+∣w3∣+∣w4∣)
- 效果：不重要的特征（如"房龄"）的权重很可能被压缩至零 。模型自动进行了特征选择，只保留了面积、卧室数等关键特征，模型更简洁、可解释性更强

7. 总结

7.1 优缺点与应用场景对比

不同的正则化技术各有千秋。

技术	核心机制	优点	缺点	典型应用场景
L1 正则化	惩罚权重绝对值之和	产生稀疏解，自动进行特征选择，模型更简洁、可解释性强	特征高度相关时选择不稳定；优化时需处理不可导点	特征维度极高且相信只有少量特征重要；需要模型压缩和特征选择的场景
L2 正则化	惩罚权重平方和	使模型更平滑稳定，有效防止过拟合；优化过程稳定（处处可导）	不产生稀疏解，所有特征都被保留	大多数回归和分类任务；特征间可能存在相关性时
Dropout	训练中随机"丢弃"神经元	类似集成学习，有效减少神经元间的共适应，鲁棒性强	训练时间通常会延长；需要调整丢弃率超参数	大规模深度神经网络（特别是全连接层多的模型）
早停法	监控验证集性能并提前停止训练	实现简单，无需修改损失函数；自动确定训练轮数	需要预留验证集；可能因验证集性能波动而过早停止	训练过程耗时长的模型；作为基础的正则化策略
数据增强	对训练数据进行合理变换以扩充数据集	直接从数据源头提升多样性；概念直观，效果显著	需要领域知识来设计有效且合理的变换方式	计算机视觉（图像变换）、自然语言处理（同义词替换）等

7.2 选择指南与实践建议

默认起点 ：当不确定时，从L2正则化开始尝试，它在大多数情况下都是一个安全且有效的选择
特征选择需求 ：当特征数量非常多，且您希望简化模型、知道哪些特征最重要时，选择L1正则化
深度学习 ：在训练深度神经网络时，常结合使用Dropout 和L2正则化 （权重衰减），并考虑使用早停法
数据匮乏 ：当训练数据量不足时，数据增强是首选的强有力工具
超参数调优 ：正则化的效果强烈依赖于超参数（如 λ λ λ ）。务必使用交叉验证来寻找最佳设置