文章目录
准确来说,二分答案应该叫做「⼆分答案 + 判断」。
⼆分答案可以处理⼤部分「最⼤值最⼩」以及「最⼩值最⼤」的问题。如果「解空间」在从⼩到⼤的「变化」过程中,「判断」答案的结果出现「⼆段性」,此时我们就可以「⼆分」这个「解空间」,通过「判断」,找出最优解。
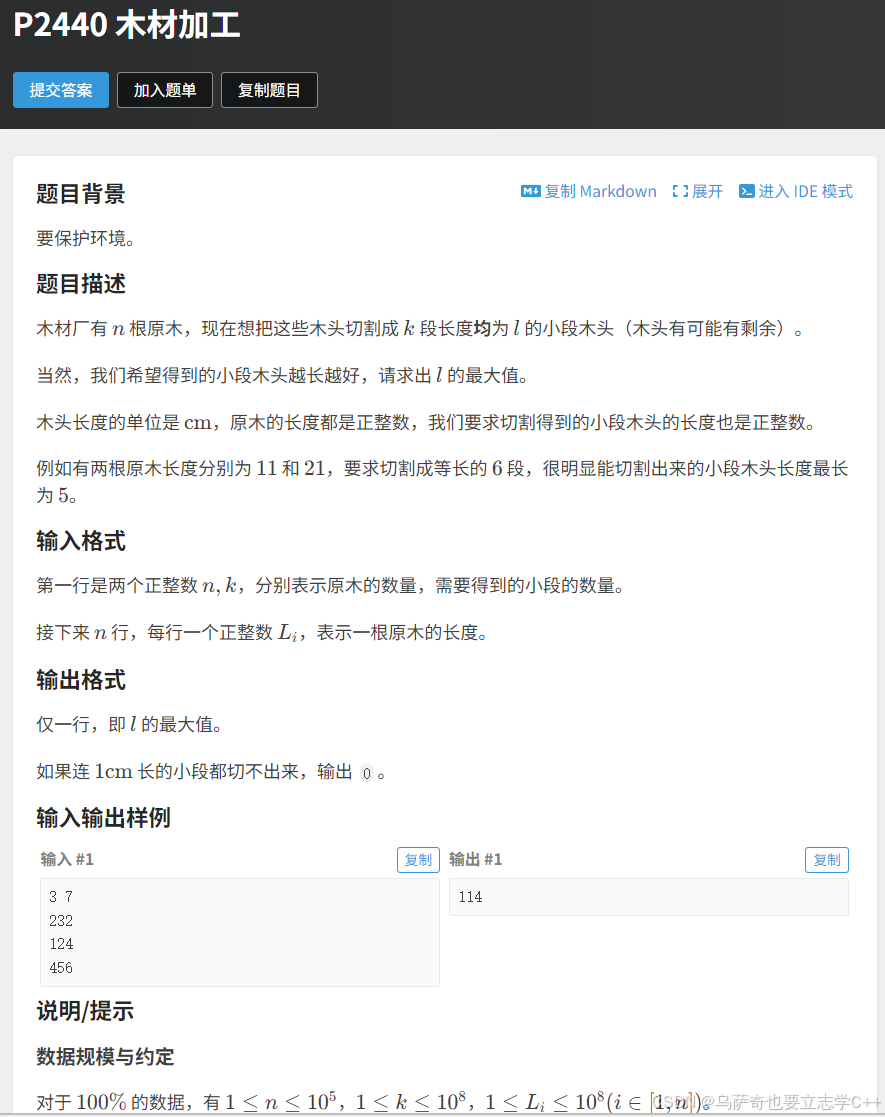
木材加工
题目描述
题目解析
首先介绍本题的暴力解法,然后从暴力解法中发现规律后进行优化。
从长度0开始枚举到最长的一根原木长度maxlen,每一个枚举长度记作x,然后求长度x的条件下一共可以切割出多少段小段木头,记作c,我们假设存储原木长度的数组为a,那么 c = a[i] / x。
从这里我们可以发现一个重要规律,随着x增大,c是必定会随之减小的,假设小段木头数量为k时对应的小段木头长度x的最大值也就是要求解的最大长度是ret,当小段木头长度x大于ret时能切割出来的小段木头数量一定是小于k的,反之当小段木头长度x小于等于ret时能切割出来的小段木头数量一定是大于等于k的,这里可以看到ret把整个解集分成了两部分,所以可以判断本题的解集是具有二段性的,可以利用二分优化。
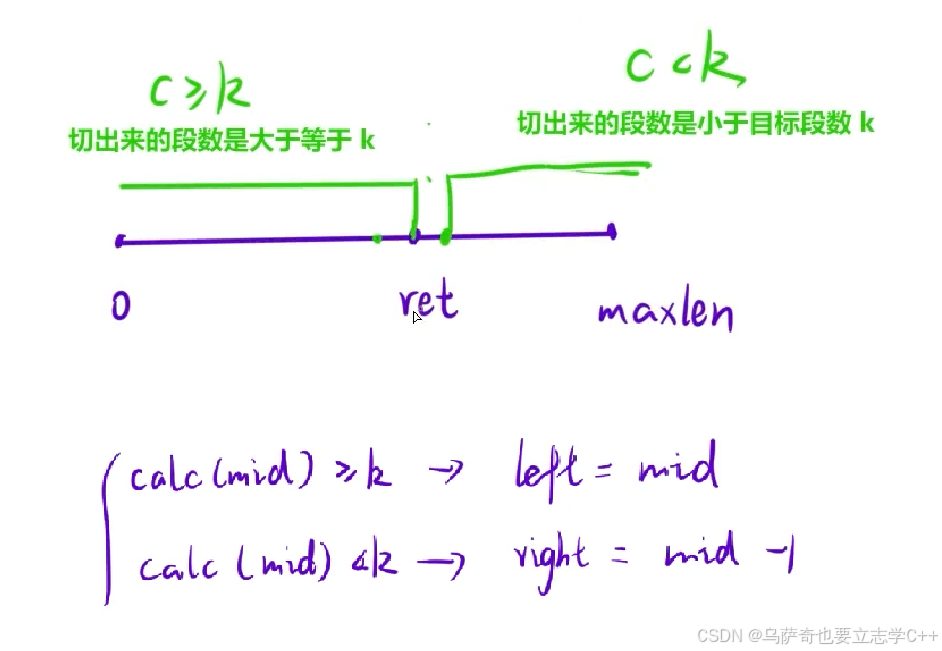
本题和之前的二分不一样,之前是求完mid后直接在判断mid落在哪个区间,而本题求完mid后还需要经过一次转化后做判断,因为本题不是以长度mid为基准划分区间的,而是以mid长度对应切出来的木头段数为基准的,所以拿到mid后还需要用calc函数求出长度mid最多能切出来的木块段数,当段数在大于等于k落在左区间时说明ret在mid的右边或者正好为mid,所以left = mid,当段数在小于k落在右区间时说明ret在mid的左边,所以right = mid - 1。
注意:本题还规定了"如果连 1cm 长的小段都切不出来,输出 0",所以left要初始化为0。
代码
cpp
#include <iostream>
using namespace std;
typedef long long LL;
const int N = 1e5 + 10;
int a[N]; //a[i]表示第i根原木长度
int n, k;
//计算小段木头长度为len时最多能切割出来的小段木头数量
int calc(int len)
{
int ret = 0;
for (int i = 1; i <= n; i++)
{
ret += (a[i] / len);
}
return ret;
}
int main()
{
cin >> n >> k;
//数据初始化
int maxlen = 0; //存储最长原木长度
for (int i = 1; i <= n; i++)
{
cin >> a[i];
maxlen = max(maxlen, a[i]);
}
//二分
LL left = 0, right = maxlen;
while (left < right)
{
LL mid = (left + right + 1) / 2;
if (calc(mid) >= k)
{
left = mid;
}
else
{
right = mid - 1;
}
}
cout << left;
return 0;
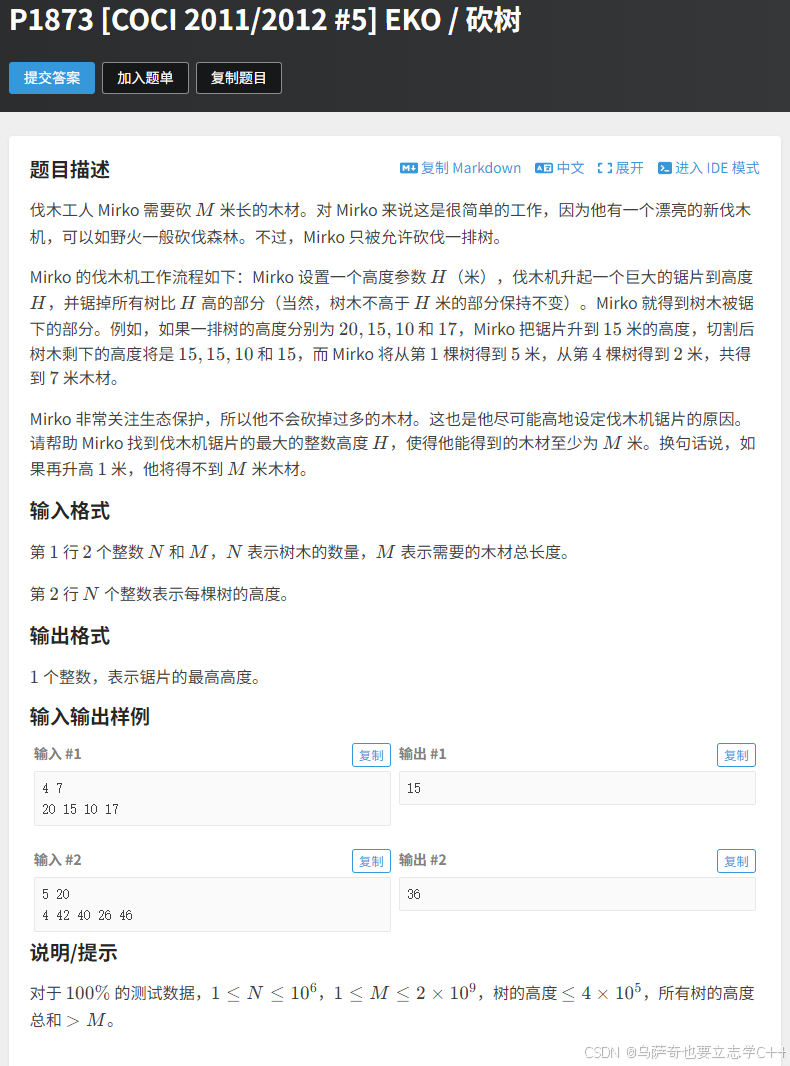
}砍树
题目描述
题目解析
10个用例过七个的原因及原始代码:
calc的返回值类型是LL,但是calc函数的返回值类型被错写成了int。
cpp
//原始错误代码
#include <iostream>
#include <algorithm>
using namespace std;
typedef long long LL;
const int N = 1e6 + 10;
LL a[N]; //a[i]表示第i棵树高度
LL n, m;
//计算锯片高度为high时能得到的木材长度
int calc(int high)
{
LL ret = 0;
for (int i = 1; i <= n; i++)
{
ret += (a[i] - high > 0 ? a[i] - high : 0);
}
return ret;
}
int main()
{
cin >> n >> m;
//初始化数据
LL maxhigh = 0;
for (int i = 1; i <= n; i++)
{
cin >> a[i];
maxhigh = max(maxhigh, a[i]);
}
//二分(锯片高度范围:0------树的最大高度)
int left = 1, right = maxhigh;
while (left < right)
{
int mid = (left + right + 1) / 2;
if (calc(mid) >= m)
{
left = mid;
}
else
{
right = mid - 1;
}
}
cout << left;
return 0;
}本题基本思路和上一题类似,小编就不赘述了。
代码
cpp
#include <iostream>
#include <algorithm>
using namespace std;
typedef long long LL;
const int N = 1e6 + 10;
int a[N]; //a[i]表示第i棵树高度
LL n, m;
//计算锯片高度为high时能得到的木材长度
LL calc(int high)
{
LL ret = 0;
for (int i = 1; i <= n; i++)
{
//ret += (a[i] - high > 0 ? a[i] - high : 0);
if (a[i] > high)
{
ret += a[i] - high;
}
}
return ret;
}
int main()
{
cin >> n >> m;
//初始化数据
int maxhigh = 0;
for (int i = 1; i <= n; i++)
{
cin >> a[i];
maxhigh = max(maxhigh, a[i]);
}
//二分(锯片高度范围:0------树的最大高度)
int left = 1, right = maxhigh;
while (left < right)
{
int mid = (left + right + 1) / 2;
if (calc(mid) >= m)
{
left = mid;
}
else
{
right = mid - 1;
}
}
cout << left << endl;
return 0;
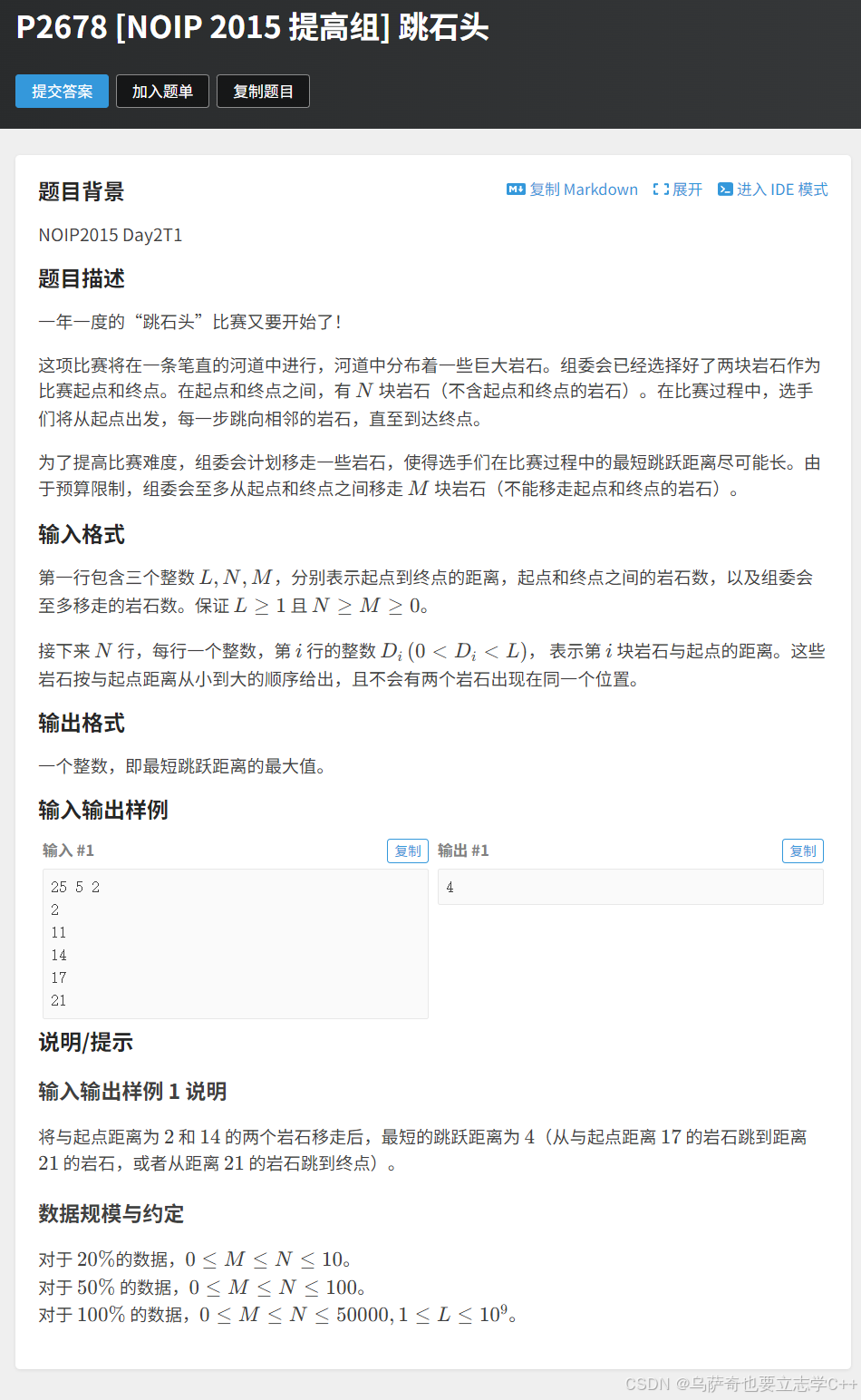
}跳石头
题目描述
题目解析
没写出正确答案原因及原始代码:
1、没分析出来二段性,没想到找最短跳跃距离和移走岩石数目之间的关系。
2、calc函数没想出写法。(应该举例子,假设一个最短跳跃距离后再思考如何移走岩石,比如在示例中假设最短跳跃距离是17)
解题思路:1、首先思考如何二分,寻找二段性。我们通过分析可知,需要移走的岩石数目是随着最短跳跃距离的增大而增大的(非严格单增),所以我们可以将最短跳跃距离作为二分对象,最短跳跃距离的最大值ret作为二分临界点,当calc(mid) <= M时说明mid <= ret,此时将left = mid,当calc(mid) > M时说明mid > ret,此时将right = mid - 1。
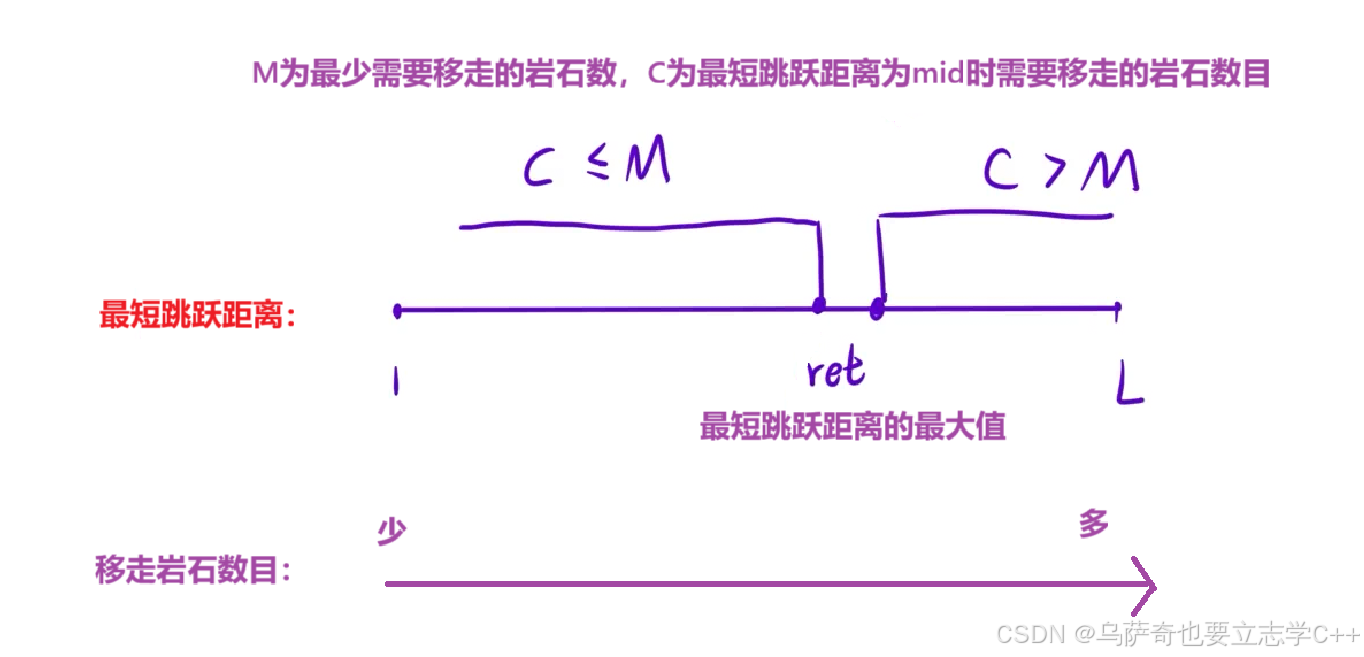
2、calc(x)需要计算出当最短跳跃距离为x时需要移走的岩石数目,calc函数实现方法:
假设最短跳跃距离是x,用两个指针i,j模拟跳跃过程,让i不动,j从i开始往后遍历,当第一次出现a[j] - a[i] >= x时,说明此时的 i->j 是一次合法跳跃,此时就需要将i和j之间的岩石全都移走,然后让i = j,继续重复上面的步骤。
当最后一步即使跳到终点了也没到最短跳跃距离时说明这个最短跳跃距离不合法,应该属于C>M这一区间,就需要把最后一步途径的全部岩石加到ret中,这样ret数目就会暴增,就会进入主函数calc(mid) > m这一分支中,让right = mid - 1。
代码
cpp
#include <iostream>
using namespace std;
const int N = 5e4 + 10;
int a[N];
int l, m, n;
//计算当最短距离为x时需要移走的岩石数目
int calc(int x)
{
int ret = 0; //需要移走的岩石数目
for (int i = 0; i <= n; i++)
{
int j = i + 1;
while(a[j] - a[i] < x && j <= n)
{
j++;
}
ret += (j - i - 1);
//原本应该是i = j,但是for循环里会i++,所以要提前减1
i = j - 1;
}
return ret;
}
int main()
{
//初始化数据
cin >> l >> n >> m;
for (int i = 1; i <= n; i++)
{
cin >> a[i];
}
a[n + 1] = l; //a[n + 1]表示起点到终点的距离
n++; //假设终点也是一个岩石,让岩石数加1
//二分
int left = 1, right = l;
while (left < right)
{
int mid = (left + right + 1) / 2;
if (calc(mid) <= m)
{
left = mid;
}
else
{
right = mid - 1;
}
}
cout << left << endl;
return 0;
}以上就是小编分享的全部内容了,如果觉得不错还请留下免费的赞和收藏
如果有建议欢迎通过评论区或私信留言,感谢您的大力支持。
一键三连好运连连哦~~
