引言
前序学习进程中，已经对CNN卷积计算使用多维卷积核展开了探索。
明确了卷积核的子卷积核数要和待进行卷积运算的矩阵通道数相等。
实际上之前的计算需要手动调整代码，展示效果也只出现了前两个。
为了提高代码运算效率，新增加了部分循环，使得整个卷积计算过程自动进行，可以直接输出完整计算效果。
定义卷积计算结果矩阵
首先定义了储存卷积计算结果的矩阵：
python
# 通过循环自动计算卷积值
# 定义步长为1
stride=1
# 定义卷积运算后的输出矩阵大小
out_h=(input_tensor_h-kernel1_h)//stride+1
out_w=(input_tensor_w-kernel1_w)//stride+1
# 为避免对原始矩阵造成破坏，新定义一个量来完全复制原始矩阵
input_cal_tensor=input_tensor
# 输出矩阵里面是所有卷积运算的效果，这个矩阵比原始矩阵小，先定义为纯0矩阵
output_cal_tensor=torch.zeros((out_h,out_w),dtype=torch.float32)定义循环计算
由于每一个子卷积核都分配了一个通道开展卷积运算，因此首先要格局子卷积核的大小把每个通道内参与计算的块取出来，然后开展卷积运算，最后把运算结果全部加到一起。
这样就要分三步走，取块，运算，求和，代码为：
python
# 循环计算
for i in range(out_h):
for j in range(out_w):
# 对原始矩阵取块进行计算，这里定义了取块的起始行
in_h_start=i*stride
# 取块的末行
in_h_end=in_h_start+kernel1_h
# 取块的起始列
in_w_start=j*stride
# 取块的末列
in_w_end=in_w_start+kernel1_w
# 这是取到的块
input_patch=input_cal_tensor[:,in_h_start:in_h_end,in_w_start:in_w_end]
# 定义一个空列表output_cal存储数据
output_cal = []
for k in range(input_tensor_channels):
# k代表了通道数，因为每个通道都要进行卷积运算，
# 因此需要先得到单通道的计算效果，然后把它们储存在列表中
output_channel=(input_patch[k]*kernel1[k]).sum()
print('input_patch[',k,']=',input_patch[k])
print('output_patch[', k, ']=', kernel1[k])
# 计算结果储存在列表中
output_cal.append(output_channel)
# 把通道效果叠加后，保存到卷积输出矩阵
# 这里有3层，第一层是每一个子卷积核和原始矩阵的每一个通道进行卷积运算
# 第二层是将第一层的卷积运算值按照顺序排放在列表output_cal中
# 第三层再将列表中获得数据直接叠加，获得当下卷积运算的总值
# 综合起来，卷积核和每一通道内的对应块对位相乘，然后全部求和，输出给当前记录卷积值的矩阵
# 由于每一个i和j都会对应k个通道，所以使用了3层循环来表达
output_cal_tensor[i, j] = sum(output_cal)
print('output_cal_tensor[', i, j, ']=', output_cal_tensor[i, j])完整代码
最后输出计算效果即可，此时的完整代码为：
python
import torch
# 1. 定义原始输入（3通道5×5）和卷积核1（边缘检测核）
input_tensor = torch.tensor([
# 输入通道1（R）：5×5
[
[1, 2, 3, 4, 5],
[6, 7, 8, 9, 10],
[11, 12, 13, 14, 15],
[16, 17, 18, 19, 20],
[21, 22, 23, 24, 25]
],
# 输入通道2（G）：5×5
[
[26, 27, 28, 29, 30],
[31, 32, 33, 34, 35],
[36, 37, 38, 39, 40],
[41, 42, 43, 44, 45],
[46, 47, 48, 49, 50]
],
# 输入通道3（B）：5×5
[
[51, 52, 53, 54, 55],
[56, 57, 58, 59, 60],
[61, 62, 63, 64, 65],
[66, 67, 68, 69, 70],
[71, 72, 73, 74, 75]
]
], dtype=torch.float32) # 形状：(3,5,5)
# 输出原始通道的形状
input_tensor_channels,input_tensor_h,input_tensor_w=input_tensor.shape
print('input_tensor_channels=',input_tensor_channels)
print('input_tensor_h=',input_tensor_h)
print('input_tensor_w=',input_tensor_w)
# 卷积核1（边缘检测核）：3个子核，每个3×3
kernel1 = torch.tensor([
[[1, 0, -1], [1, 0, -1], [1, 0, -1]], # 子核1（R通道）
[[1, 0, -1], [1, 0, -1], [1, 0, -1]], # 子核2（G通道）
[[1, 0, -1], [1, 0, -1], [1, 0, -1]] # 子核3（B通道）
], dtype=torch.float32) # 形状：(3,3,3)
# 输出卷积核的形状
kernel1_channels,kernel1_h,kernel1_w=kernel1.shape
print('kernel1_channels=',kernel1_channels)
print('kernel1_h=',kernel1_h)
print('kernel1_w=',kernel1_w)
# 2. 计算(0,0)位置的像素值（左上方3×3区域）
print("=== (0,0)位置计算（左上方3×3）===")
# 直接通过索引范围提取3×3区域（行0-2，列0-2）
input_r_00 = input_tensor[0, 0:kernel1_h, 0:kernel1_w] # R通道：行0-2，列0-2
input_g_00 = input_tensor[1, 0:kernel1_h, 0:kernel1_w] # G通道：行0-2，列0-2
input_b_00 = input_tensor[2, 0:kernel1_h, 0:kernel1_w] # B通道：行0-2，列0-2
r_00 = (input_r_00 * kernel1[0]).sum()
g_00 = (input_g_00 * kernel1[1]).sum()
b_00 = (input_b_00 * kernel1[2]).sum()
pixel_00 = r_00 + g_00 + b_00
print(f"R通道结果：{r_00.item():.0f} | G通道结果：{g_00.item():.0f} | B通道结果：{b_00.item():.0f}")
print(f"(0,0)像素最终值：{pixel_00.item():.0f}\n")
# 3. 计算(0,1)位置的像素值（卷积核右移1步）
print("=== (0,1)位置计算（右移1步的3×3）===")
# 直接通过索引范围提取右移后的3×3区域（行0-2，列1-3）
input_r_01 = input_tensor[0, 0:kernel1_h, 1:1+kernel1_w] # R通道：行0-2，列1-3
input_g_01 = input_tensor[1, 0:kernel1_h, 1:1+kernel1_w] # G通道：行0-2，列1-3
input_b_01 = input_tensor[2, 0:kernel1_h, 1:1+kernel1_w] # B通道：行0-2，列1-3
r_01 = (input_r_01 * kernel1[0]).sum()
g_01 = (input_g_01 * kernel1[1]).sum()
b_01 = (input_b_01 * kernel1[2]).sum()
pixel_01 = r_01 + g_01 + b_01
print(f"R通道结果：{r_01.item():.0f} | G通道结果：{g_01.item():.0f} | B通道结果：{b_01.item():.0f}")
print(f"(0,1)像素最终值：{pixel_01.item():.0f}")
# 通过循环自动计算卷积值
# 定义步长为1
stride=1
# 定义卷积运算后的输出矩阵大小
out_h=(input_tensor_h-kernel1_h)//stride+1
out_w=(input_tensor_w-kernel1_w)//stride+1
# 为避免对原始矩阵造成破坏，新定义一个量来完全复制原始矩阵
input_cal_tensor=input_tensor
# 输出矩阵里面是所有卷积运算的效果，这个矩阵比原始矩阵小，先定义为纯0矩阵
output_cal_tensor=torch.zeros((out_h,out_w),dtype=torch.float32)
# 循环计算
for i in range(out_h):
for j in range(out_w):
# 对原始矩阵取块进行计算，这里定义了取块的起始行
in_h_start=i*stride
# 取块的末行
in_h_end=in_h_start+kernel1_h
# 取块的起始列
in_w_start=j*stride
# 取块的末列
in_w_end=in_w_start+kernel1_w
# 这是取到的块
input_patch=input_cal_tensor[:,in_h_start:in_h_end,in_w_start:in_w_end]
# 定义一个空列表output_cal存储数据
output_cal = []
for k in range(input_tensor_channels):
# k代表了通道数，因为每个通道都要进行卷积运算，
# 因此需要先得到单通道的计算效果，然后把它们储存在列表中
output_channel=(input_patch[k]*kernel1[k]).sum()
print('input_patch[',k,']=',input_patch[k])
print('output_patch[', k, ']=', kernel1[k])
# 计算结果储存在列表中
output_cal.append(output_channel)
# 把通道效果叠加后，保存到卷积输出矩阵
# 这里有3层，第一层是每一个子卷积核和原始矩阵的每一个通道进行卷积运算
# 第二层是将第一层的卷积运算值按照顺序排放在列表output_cal中
# 第三层再将列表中获得数据直接叠加，获得当下卷积运算的总值
# 综合起来，卷积核和每一通道内的对应块对位相乘，然后全部求和，输出给当前记录卷积值的矩阵
# 由于每一个i和j都会对应k个通道，所以使用了3层循环来表达
output_cal_tensor[i, j] = sum(output_cal)
print('output_cal_tensor[', i, j, ']=', output_cal_tensor[i, j])
print('output=',output_cal_tensor)计算效果
代码运行后输出了很多内容，这里给出综合效果：
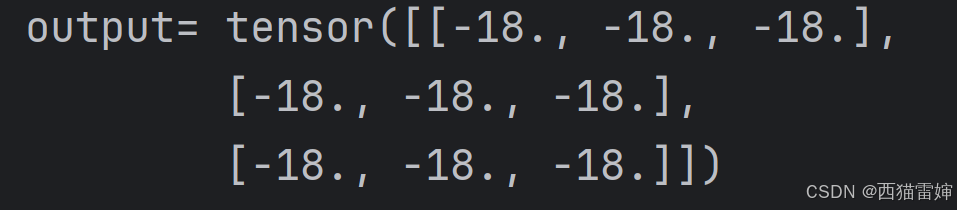使用循环计算后，完整计算效果快速展示，计算效率获得提升。
总结
对CNN多维卷积核自动计算的方法展开了探索。