TAC: 线性多智能体系统的时变编队队形跟踪与协同围捕研究

TAC: 多目标跟踪时变编队队形多目标协同围捕预定义时间凸组合研究了具有多领导者的线性多智能体系统的时变队形跟踪问题，其中follower的状态在跟踪多个领导者状态的凸组合时形成一个预定义的时变队形。追随者分为知者和知者，知者的邻居集包含所有领导者，知者的邻居集不包含领导者。利用相邻的相对信息构造了编队跟踪协议。利用拉普拉斯矩阵的性质，给出了具有多领导者的多智能体系统实现时变队列跟踪的充分必要条件，并给出了队列跟踪的可行性约束。通过求解代数Riccati方程，提出了一种设计地层跟踪协议的方法。所得结果可用于处理具有一个或多个目标/领导者的线性多智能体系统的时变队形跟踪问题、目标封闭问题和共识跟踪问题。

当一群无人机需要执行动态编队搜索任务，或是工业机器人协作搬运不规则物体时，如何让智能体在移动中自主调整队形？我们实验室最近在调试多智能体协同算法时，发现基于TAC（Tracking-Adjusting-Controlling）框架的时变编队方案很有意思。特别是针对多领导者场景的凸组合追踪策略，能实现类似狼群围捕猎物的动态队形变换。

先看个实际场景：假设红蓝两队无人机需要围捕三个移动目标，每架追随者无人机需要根据邻居的位置信息实时调整飞行轨迹。这里有个关键设定------部分"知者"可以直接获取领导者的位置（相当于狼群中的哨兵），而普通成员只能获取相邻同伴的信息。这种信息不对称的结构直接影响着编队稳定性。

构造拉普拉斯矩阵时，我们采用了分层处理。用Python实现的通信拓扑结构生成器大概长这样：

python 复制代码

def build_laplacian(leaders, informed_followers, regular_followers):
    n = len(leaders) + len(informed_followers) + len(regular_followers)
    L = np.zeros((n, n))
    
    leader_indices = range(len(leaders))
    for i in leader_indices:
        for j in leader_indices:
            L[i,j] = -1 if i != j else len(leaders)-1
    
    # 知者与领导者的连接
    offset = len(leaders)
    for idx, f in enumerate(informed_followers):
        pos = offset + idx
        L[pos, :len(leaders)] = -1
        L[pos, pos] = len(leaders)
    
    # 普通追随者之间的环形连接
    # ...(略)...
    
    return L

这段代码的核心在于分层处理通信权重。领导者之间形成全连通网络（对应拉普拉斯矩阵左上块的非零元素），而知者节点会与所有领导者建立连接（中间块的负权值）。这种结构保证了领导层状态变化能有效传递到知者层。

协议设计中比较tricky的是预定义时间收敛条件的实现。我们在MATLAB里验证代数Riccati方程时发现，权重矩阵Q的选择直接影响收敛速度：

matlab 复制代码

% 预定义收敛时间T=5s
rho = 2/(pi*T);
[K,S,e] = care(A', C', rho*B*B', Q);

这里通过调节rho参数将时间约束融入方程求解。有个反直觉的现象：当领导者数量增加时，Q矩阵需要适当降低对位置误差的惩罚权重，否则会导致控制量剧烈震荡。这可能与多领导者带来的冗余信息有关。

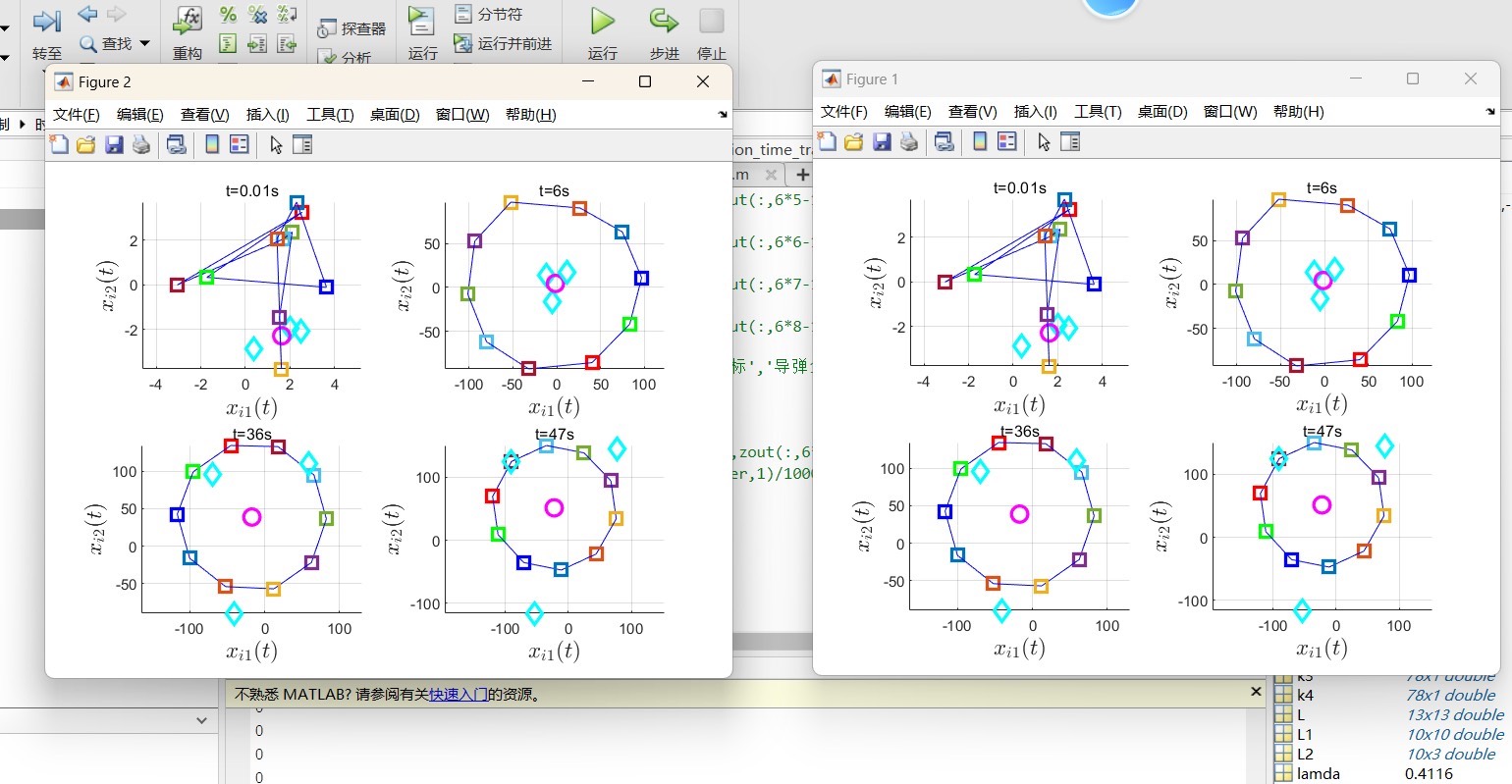
在无人机围捕动态仿真中（用ROS+Gazebo搭建），我们观察到当三个目标突然分散移动时，追随者群体会自动分裂成子编队进行包抄。这种自发涌现的行为背后，正是凸组合系数在起作用------每个追随者实际追踪的是领导者的加权平均位置，而权重系数根据相对距离动态调整。

这种方法的局限在于通信延迟敏感。实测中当延迟超过200ms时，拉普拉斯矩阵的特征值分布会进入不稳定区域。不过加入预测补偿模块后效果明显改善，当然这就是另一个故事了。

下次如果看到无人机表演中突然出现太极八卦阵型变换，说不定背后就是类似的算法在支撑。多智能体协同的美妙之处，就在于简单规则能催生复杂行为，不是吗？