目录
上一周,在写力扣hot堆的题目。其实堆最常见的问题就是TOP-K问题。感觉很大一部分问题都可以使用TOP-K问题的思路去解决。但是另一方面,其实堆也可以使用快速选择的方法去解决(基于快速排序)这往往经过三数取中法的优化后,可以达到O(N)的时间复杂度,由于TOP-K问题的时间复杂度O(NlogK)。而且我认为写这个题,不能太依靠PriorityQueue容器,也需要自己手动实现一个大根堆/小根堆。
关于快速排序(使用挖空法实现+三数取中法+直接插入的优化)常见算法的总结与实现思路_常见算法实现-CSDN博客
快速选择法与TOP-K问题的抉择
TOP-K法比较稳定 好情况坏情况都是O(Nlogk)
快速选择不稳定 坏情况O(N^2) 平均情况O(N)
题目链接
215. 数组中的第K个最大元素 - 力扣(LeetCode)
数组中的第K个最大元素
法一:TOP-K思路&&代码
TOP-K:
找前K个最大的元素,建小根堆,先放入K个元素,剩下的N-K元素与堆顶进行比较,如果大于堆顶元素,则替换堆顶即可
找前K个最小的元素,建大根堆,先放入K个元素,剩下的N-K元素与堆顶进行比较,如果小于堆顶元素,则替换堆顶即可

java
class Solution {
public int findKthLargest(int[] nums, int k) {
if(k==1&&nums.length==1){
return nums[0];
}
//创建个小根堆
PriorityQueue<Integer> maxHeap=new PriorityQueue<>((a,b)->a-b);
for(int i=0;i<k;i++){
maxHeap.offer(nums[i]);
}
for(int i=k;i<nums.length;i++){
//如果大于堆顶则替换
if(nums[i]>maxHeap.peek()){
maxHeap.poll();
maxHeap.offer(nums[i]);
}
}
// while(maxHeap.size()>1){
// maxHeap.poll();
// }
return maxHeap.poll();
}
}法二:手动实现一个大根堆思路&&代码
手动实现一个大根堆,交换堆尾与堆顶元素 向下调整 使得数组达到升序
java
class Solution {
public int findKthLargest(int[] nums, int k) {
if(k==1&&nums.length==1){
return nums[0];
}
//手动实现升序数组
//则创建大根堆
//然后交换最后一个与堆顶
heapsort(nums);
int m=0;
for(int i=nums.length-1;i>=0;i--){
m++;
if(m==k){
return nums[i];
}
}
return -1;
}
public void heapsort(int[] nums){
//创建大根堆
createMaxHeap(nums);
//交换堆尾和堆顶
int end=nums.length-1;
while(end>0){
swap(nums,0,end);
//向下调整
siftdown(nums,0,end);
end--;
}
}
public void createMaxHeap(int[] nums){
for(int parent=(nums.length-1-1)/2;parent>=0;parent--){
//找第一个非叶子的节点
//向下调整
siftdown(nums,parent,nums.length);
}
}
public void siftdown(int[] nums,int parent,int length){
int child=2*parent+1;
while(child<length){
//找左右子节点种的较大的那个
if(child+1<length&&nums[child+1]>nums[child]){
child++;
}
if(nums[child]>nums[parent]){
swap(nums,parent,child);
parent=child;
child=2*parent+1;
}else{
break;
}
}
}
public void swap(int[] nums,int i,int j){
int tmp=nums[i];
nums[i]=nums[j];
nums[j]=tmp;
}
}法三:快速选择思路&&代码

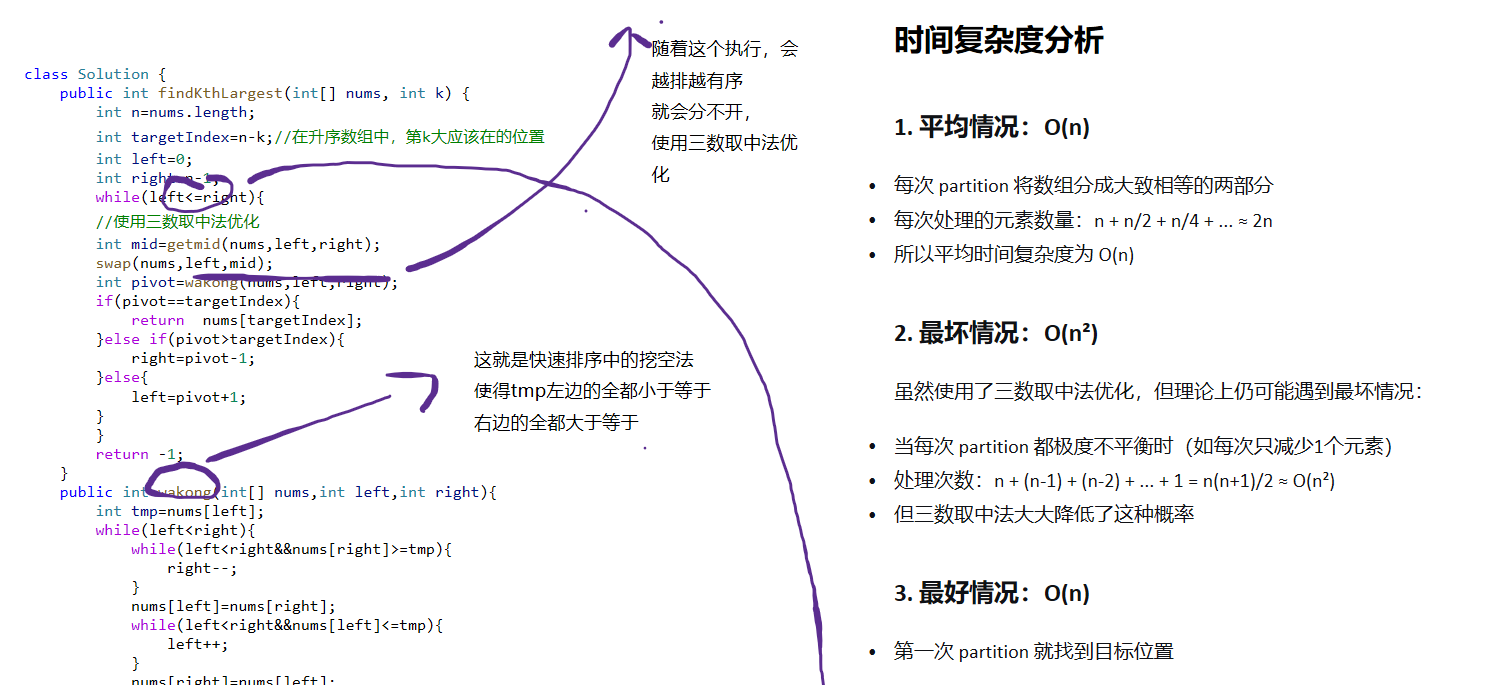

java
class Solution {
public int findKthLargest(int[] nums, int k) {
int n=nums.length;
int targetIndex=n-k;//在升序数组中,第k大应该在的位置
int left=0;
int right=n-1;
while(left<=right){
//使用三数取中法优化
int mid=getmid(nums,left,right);
swap(nums,left,mid);
int pivot=wakong(nums,left,right);
if(pivot==targetIndex){
return nums[targetIndex];
}else if(pivot>targetIndex){
right=pivot-1;
}else{
left=pivot+1;
}
}
return -1;
}
public int wakong(int[] nums,int left,int right){
int tmp=nums[left];
while(left<right){
while(left<right&&nums[right]>=tmp){
right--;
}
nums[left]=nums[right];
while(left<right&&nums[left]<=tmp){
left++;
}
nums[right]=nums[left];
}
nums[left]=tmp;
return left;
}
public void swap(int[] nums,int i,int j){
int tmp=nums[i];
nums[i]=nums[j];
nums[j]=tmp;
}
public int getmid(int[] nums,int left,int right){
int midIndex=left+(right-left)/2;
if(nums[left]<nums[right]){
if(nums[midIndex]>nums[right]){
return right;
}else if(nums[midIndex]<nums[left]){
return left;
}else{
return midIndex;
}
}else{
if(nums[midIndex]<nums[right]){
return right;
}else if(nums[midIndex]>nums[left]){
return left;
}else{
return midIndex;
}
}
}
}前K个高频元素
法一:TOP-K思路&&代码
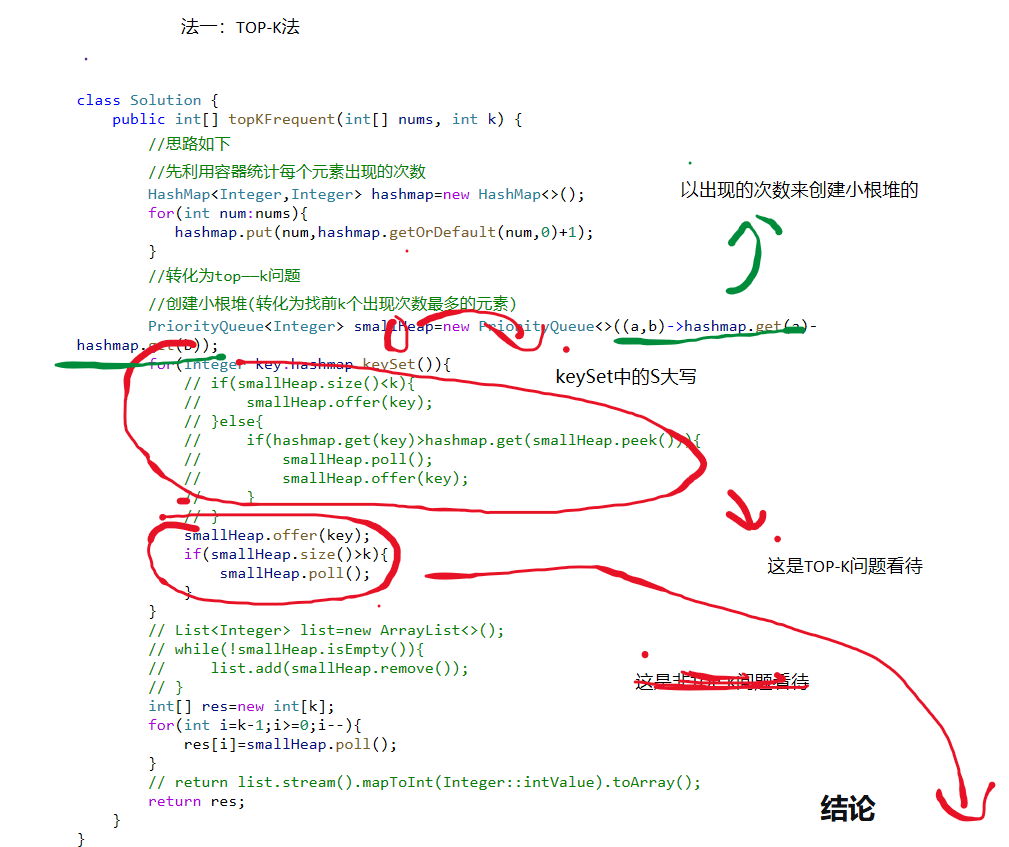

java
class Solution {
public int[] topKFrequent(int[] nums, int k) {
//思路如下
//先利用容器统计每个元素出现的次数
HashMap<Integer,Integer> hashmap=new HashMap<>();
for(int num:nums){
hashmap.put(num,hashmap.getOrDefault(num,0)+1);
}
//转化为top------k问题
//创建小根堆(转化为找前k个出现次数最多的元素)
PriorityQueue<Integer> smallHeap=new PriorityQueue<>((a,b)->hashmap.get(a)-hashmap.get(b));
for(Integer key:hashmap.keySet()){
// if(smallHeap.size()<k){
// smallHeap.offer(key);
// }else{
// if(hashmap.get(key)>hashmap.get(smallHeap.peek())){
// smallHeap.poll();
// smallHeap.offer(key);
// }
// }
smallHeap.offer(key);
if(smallHeap.size()>k){
smallHeap.poll();
}
}
// List<Integer> list=new ArrayList<>();
// while(!smallHeap.isEmpty()){
// list.add(smallHeap.remove());
// }
int[] res=new int[k];
for(int i=k-1;i>=0;i--){
res[i]=smallHeap.poll();
}
// return list.stream().mapToInt(Integer::intValue).toArray();
return res;
}
}法二:快速选择法思路&&代码
其实这个解法跟数组中的第K个最大元素的快速选择法是差不多的,只不过这个是二维数组而已
java
class Solution {
public int[] topKFrequent(int[] nums, int k) {
//使用快速选择
HashMap<Integer,Integer> hashmap=new HashMap<>();
for(int num:nums){
hashmap.put(num,hashmap.getOrDefault(num,0)+1);
}
//创建一个二维数组 横坐标代表元素 纵坐标代码该元素的个数
int n=hashmap.size();
int[][] element=new int[n][2];
int index=0;
for(HashMap.Entry<Integer, Integer> entry : hashmap.entrySet()) {
element[index][0] = entry.getKey(); // 数字
element[index][1] = entry.getValue(); // 频率
index++;
}
int left=0;
int right=n-1;
int targetIndex=n-k;//按频率升序,应该再nums.length-k位置
while(left<=right){
//使用三数取中法优化
int mid=getMid(element,left,right);
swap(element,left,mid);
int pivot=wakong(element,left,right);
if(pivot==targetIndex){
break;
}else if(pivot>targetIndex){
right=pivot-1;
}else{
left=pivot+1;
}
}
int[] res=new int[k];
for(int i=0;i<k;i++){
res[i]=element[n-1-i][0];
}
return res;
}
public int wakong(int[][] nums,int left,int right){
int tmp=nums[left][0];
int tmp_count=nums[left][1];
while(left<right){
while(left<right&&nums[right][1]>=tmp_count){
right--;
}
nums[left][0]=nums[right][0];
nums[left][1]=nums[right][1];
while(left<right&&nums[left][1]<=tmp_count){
left++;
}
nums[right][0]=nums[left][0];
nums[right][1]=nums[left][1];
}
nums[left][0]=tmp;
nums[left][1]=tmp_count;
return left;
}
public int getMid(int[][] nums,int left,int right){
// int mid=left+(right-left)/2;
// if(nums[left][1]<nums[right][1]){
// if(nums[mid][1]>nums[right][1]){
// return right;
// }else if(nums[mid][1]<nums[left][1]){
// return left;
// }else{
// return mid;
// }
// }else{
// if(nums[mid][1]>nums[left][1]){
// return left;
// }else if(nums[mid][1]<nums[right][1]){
// return right;
// }else{
// return mid;
// }
// }
int mid = left + (right - left) / 2;
// 直接比较三个位置的频率值
int leftFreq = nums[left][1];
int midFreq = nums[mid][1];
int rightFreq = nums[right][1];
// 返回中间值的索引
if ((leftFreq - midFreq) * (leftFreq - rightFreq) <= 0) return left;
if ((midFreq - leftFreq) * (midFreq - rightFreq) <= 0) return mid;
return right;
}
public void swap(int[][] element,int i,int j){
int[] tmp=element[i];
element[i]=element[j];
element[j]=tmp;
}
}法三:手动实现一个小根堆思路&&代码
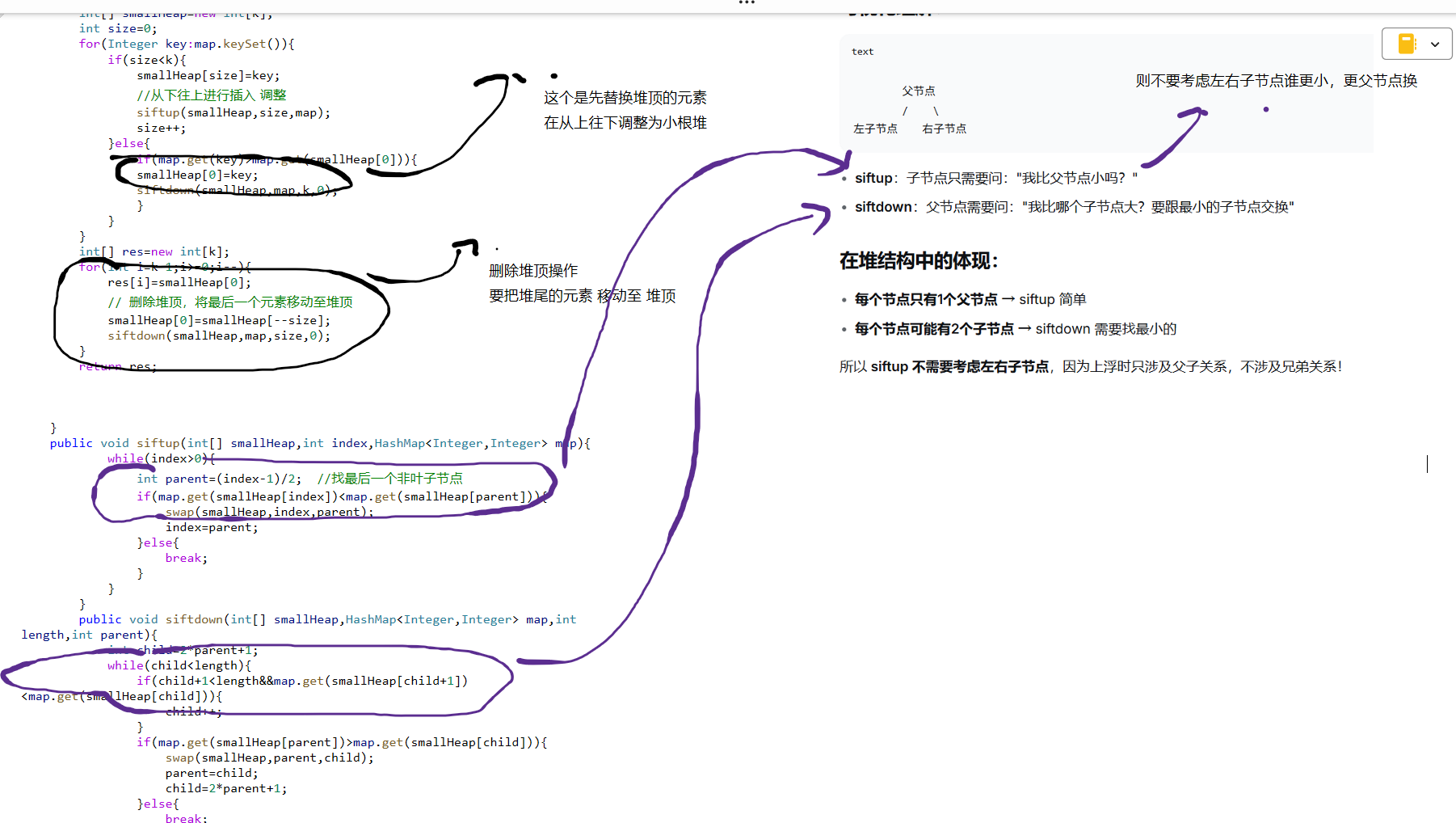
java
class Solution {
public int[] topKFrequent(int[] nums, int k) {
HashMap<Integer,Integer> map=new HashMap<>();
for(int num:nums){
map.put(num,map.getOrDefault(num,0)+1);
}
//手动实现一个小根堆
int[] smallHeap=new int[k];
int size=0;
for(Integer key:map.keySet()){
if(size<k){
smallHeap[size]=key;
//从下往上进行插入 调整
siftup(smallHeap,size,map);
size++;
}else{
if(map.get(key)>map.get(smallHeap[0])){
smallHeap[0]=key;
siftdown(smallHeap,map,k,0);
}
}
}
int[] res=new int[k];
for(int i=k-1;i>=0;i--){
res[i]=smallHeap[0];
// 删除堆顶,将最后一个元素移动至堆顶
smallHeap[0]=smallHeap[--size];
siftdown(smallHeap,map,size,0);
}
return res;
}
public void siftup(int[] smallHeap,int index,HashMap<Integer,Integer> map){
while(index>0){
int parent=(index-1)/2; //找最后一个非叶子节点
if(map.get(smallHeap[index])<map.get(smallHeap[parent])){
swap(smallHeap,index,parent);
index=parent;
}else{
break;
}
}
}
public void siftdown(int[] smallHeap,HashMap<Integer,Integer> map,int length,int parent){
int child=2*parent+1;
while(child<length){
if(child+1<length&&map.get(smallHeap[child+1])<map.get(smallHeap[child])){
child++;
}
if(map.get(smallHeap[parent])>map.get(smallHeap[child])){
swap(smallHeap,parent,child);
parent=child;
child=2*parent+1;
}else{
break;
}
}
}
public void swap(int[] nums,int i,int j){
int tmp=nums[i];
nums[i]=nums[j];
nums[j]=tmp;
}
}