Channel Estimation for mmWave High-Mobility Systems With 5G New Radio OFDM (I)

摘要------时变信道受多普勒效应的显著影响，导致信道增益快速变化，需要进行多普勒频率估计以补偿信道相移并提高通信质量。在本文中，针对高移动性场景下的时变信道估计，我们提出了一种基于第五代（5G）新空口（NR）正交频分复用（OFDM）的新型传输结构。通过设计合适的子载波间隔和时隙格式，我们确保导频信号在单个时隙内几乎保持不变，并在不同时隙之间表现出旋转不变性。利用这种旋转不变性，我们引入了一种基于范德蒙（Vandermonde）结构张量分解的新型算法，该算法是非迭代的，且比其他基于张量的算法具有更低的计算复杂度和更高的鲁棒性。

此外，我们提供了张量分解唯一性条件的理论分析，证明了所提出的算法具有很强的可行性，且所需的导频开销较低。我们还分析了参数估计的均方误差（MSE），并给出了克拉美-罗界（CRB）的简明推导。结果表明，在中高信噪比（SNR）下，所提出的算法在参数估计性能方面显著优于基于压缩感知（CS）的方法和其他基于张量的方法。

此外，基于瞬时信道模型的所提算法比依赖统计信道模型的基于卡尔曼滤波的算法具有更高的信道估计精度。使用 Wireless InSite（构建真实世界散射环境）生成的信道数据进行的仿真结果证明了所提算法的高估计精度，验证了其在实际场景中的有效性。

索引词------时变信道估计，毫米波（mmWave）通信，MIMO-OFDM，混合预编码。

文章目录

• • [I. INTRODUCTION](#I. INTRODUCTION)
  • [II. NOTATIONS AND PRELIMINARIES](#II. NOTATIONS AND PRELIMINARIES)
  • • [B. Tensor Preliminaries](#B. Tensor Preliminaries)
  • [III. SYSTEM MODEL](#III. SYSTEM MODEL)
  • • [B. Proposed Transmission Structure Based on 5G NR](#B. Proposed Transmission Structure Based on 5G NR)
    • [C. Signal Model](#C. Signal Model)

I. INTRODUCTION

现有的文献 [4], [5], [6], [7], [8], [9], [10] 对毫米波 MIMO 系统的信道估计进行了广泛的研究。例如，利用毫米波信道的稀疏特性，压缩感知 (CS) 信道估计方法被应用于毫米波 MIMO 系统 [4], [5], [6] 中。在文献 [7], [8], [9] 和 [10] 中，频率选择性 MIMO 信道估计问题通过基于张量分解的方法得到了解决。为了评估信道估计算法的性能，克拉美-罗界 (CRB) 被广泛采用，因为它表征了理论性能极限，作为评估算法精度的基准 [4], [11], [12], [13]。

值得注意的是，上述研究主要假设频率选择性、时不变信道，而未考虑高移动性场景。在毫米波 MIMO 高移动性环境中，包括高速公路 [14]、高速列车 [15], [16]、无人机 (UAVs) [17] 和其他场景，信道受高多普勒效应影响并快速变化，这给高速率和可靠通信带来了挑战。在毫米波 MIMO 高移动性场景中，精确的信道估计有助于补偿信道相移并提高服务质量。然而，在高移动性场景中，信道的快速变化导致了额外的导频开销和较差的估计性能。为了解决这个问题，一些文献研究了高移动性场景下毫米波 MIMO 系统的信道估计 [18], [19], [20], [21], [22], [23], [24]。

• 在文献 [18] 和 [19] 中，信道估计问题是利用基于正交匹配追踪 (OMP) 的方法解决的。然而，由于 OMP 中使用了网格搜索，参数估计的分辨率受到了限制。

• 在文献 [20] 和 [21] 中，提出了一种基于张量分解的 MIMO 系统信道估计方法。尽管如此，该方法依赖于交替最小二乘 (ALS) 算法，这是一种迭代算法，并且当张量秩超过 2 时，其收敛性可能无法保证 [25]。

• 在文献 [22] 中，作者研究了基于卡尔曼滤波 (KF)-CS 算法的 MIMO 正交频分复用 (OFDM) 系统信道估计。

• 在文献 [23] 和 [24] 中，基于卡尔曼滤波的稀疏贝叶斯学习 (KF-SBL) 框架被应用于毫米波 MIMO-OFDM 信道估计。然而，基于 SBL 的算法计算复杂度较高。

此外，由于高移动性场景下的信道相干时间减少，传输结构通常必须支持低导频开销和低系统复杂度。在先前的研究 [18], [19], [22], [23] 和 [24] 中，导频信号通常插入每一帧的初始时隙以估计角度信息，以及随后的所有时隙以更新信道增益。这种传输方案导致了大量的导频开销和高系统复杂度，因为必须在随后的数据传输过程中重复执行信道估计操作。

然而，在典型的车载通信场景中，车辆相对于基站 (BS) 的相对位置在一帧的持续时间内（例如，5G 新空口 (5G NR) 中的 10 ms）几乎保持不变，使得大尺度信道参数可以被视为准静态的。因此，在每一帧的初始时隙内估计所有大尺度信道信息（如角度、时延、增益和多普勒频率）是完全可行的。获得的信息随后可用于后续传输中的信道均衡和相位补偿，从而消除了在后续数据传输期间重复插入导频信号的需要。据我们所知，目前没有任何文献探索 5G NR 标准来设计专门用于高移动性场景下多普勒频率估计的系统配置。

受上述讨论的启发，在本文中，我们基于瞬时信道模型研究了高移动性场景下混合结构毫米波大规模 MIMO-OFDM 系统的上行链路信道估计。本文的主要贡献总结如下：

• 传输结构设计： 我们提出了一种基于 5G NR [26] 的面向高移动性场景的新型传输结构。具体而言，我们分析了毫米波频段中适当的子载波间隔和时隙格式，这有利于解决高移动性场景中的多普勒频率估计问题，而这在现有文献中尚未被探索。与现有的传输结构相比，所提出的方案降低了系统复杂度。

• 新型信道估计框架： 基于所提出的传输结构，我们对高移动性场景下的 MIMO-OFDM 信号进行建模，并制定了信道估计问题。我们通过充分利用因子矩阵的范德蒙 (Vandermonde) 结构，提出了一种基于张量分解的信道估计方法，这得益于我们提出的传输方案中不同时隙导频信号的旋转不变性。所提出的方法是非迭代的，且计算效率高。

• 理论分析： 分析了针对所提出的四阶张量模型的正则多维 (CP) 分解的唯一性条件。我们证明了所提出的方法在比现有张量分解算法更宽松的条件下实现了唯一性，这意味着降低了导频开销并提高了鲁棒性。此外，我们详细分析了与参数估计相关的均方误差 (MSEs)。还给出了克拉美-罗界 (CRB) 的更简明的推导，该推导避免了沿所有维度展开高阶张量的需要，并消除了计算费希尔信息矩阵 (FIM) 时的复杂元素索引 [12], [27]。

• 有效性验证： 仿真结果表明，与基准方法相比，特别是在中高信噪比 (SNR) 区域，所提出的算法在角度、时延和多普勒频率方面实现了显著更高的估计精度。此外，为了评估在真实仿真环境中的性能，使用 Wireless InSite 射线追踪模拟器 [28] 生成的信道数据对所提出的方法进行了评估。结果表明，所提出的算法表现出很高的估计精度，并在复杂的散射无线环境中优于基于 KF 的方法和其他基准，从而验证了所提出方法在实际应用中的有效性。

II. NOTATIONS AND PRELIMINARIES

B. Tensor Preliminaries

为了更好的可读性，这里提供了一些关于张量和 CP 分解的预备知识。更多详细信息可以在 [29] 和 [30] 中找到。

在本文中，张量表示多维数组 [29]。纤维（Fiber）定义为张量的一维切片，通过固定除一个索引外的所有索引形成。切片（Slice）是张量的二维截面，通过固定除两个索引外的所有索引形成。如果一个 N N N 阶张量 X ∈ C I 1 × I 2 × ⋯ × I N \boldsymbol{\mathcal{X}} \in \mathbb{C}^{I_1 \times I_2 \times \cdots \times I_N} X∈CI1×I2×⋯×IN 可以表示为 N N N 个向量的外积，则称其为秩-1 张量，即：

X = a ( 1 ) ∘ a ( 2 ) ∘ ⋯ ∘ a ( N ) , a ( i ) ∈ C I i × 1 . (1) \boldsymbol{\mathcal{X}} = \mathbf{a}^{(1)} \circ \mathbf{a}^{(2)} \circ \cdots \circ \mathbf{a}^{(N)}, \quad \mathbf{a}^{(i)} \in \mathbb{C}^{I_i \times 1}. \tag{1} X=a(1)∘a(2)∘⋯∘a(N),a(i)∈CIi×1.(1)

CP 分解将 N N N 阶张量 X ∈ C I 1 × I 2 × ⋯ × I N \boldsymbol{\mathcal{X}} \in \mathbb{C}^{I_1 \times I_2 \times \cdots \times I_N} X∈CI1×I2×⋯×IN 表示为秩-1 张量的和，即：

X = ∑ r = 1 R a r ( 1 ) ∘ a r ( 2 ) ∘ ⋯ ∘ a r ( N ) , (2) \boldsymbol{\mathcal{X}} = \sum_{r=1}^{R} \mathbf{a}_r^{(1)} \circ \mathbf{a}_r^{(2)} \circ \cdots \circ \mathbf{a}_r^{(N)}, \tag{2} X=r=1∑Rar(1)∘ar(2)∘⋯∘ar(N),(2)

其中 R R R 是张量秩。第 n n n 模的因子矩阵定义为 A ( n ) ≜ [ a 1 ( n ) , ... , a R ( n ) ] ∈ C I n × R \mathbf{A}^{(n)} \triangleq \left[ \mathbf{a}_1^{(n)}, \ldots, \mathbf{a}_R^{(n)} \right] \in \mathbb{C}^{I_n \times R} A(n)≜[a1(n),...,aR(n)]∈CIn×R。那么，公式 (2) 可以等价地表示为

X = I N , R × 1 A ( 1 ) × 2 A ( 2 ) × 3 ⋯ × N A ( N ) = ⟦ A ( 1 ) , A ( 2 ) , ... , A ( N ) ⟧ , \begin{aligned} \boldsymbol{\mathcal{X}} &= \boldsymbol{\mathcal{I}}_{N,R} \times_1 \mathbf{A}^{(1)} \times_2 \mathbf{A}^{(2)} \times_3 \cdots \times_N \mathbf{A}^{(N)} \\ &= \llbracket \mathbf{A}^{(1)}, \mathbf{A}^{(2)}, \ldots, \mathbf{A}^{(N)} \rrbracket, \end{aligned} X=IN,R×1A(1)×2A(2)×3⋯×NA(N)=[[A(1),A(2),...,A(N)]],

I N , R \boldsymbol{\mathcal{I}}_{N,R} IN,R：这是一个 N N N 阶的超对角张量（Identity Tensor / Diagonal Tensor），尺寸为 R × R × ⋯ × R R \times R \times \cdots \times R R×R×⋯×R。

• 它的特点是：只有在所有索引都相等的位置（即 ( r , r , ... , r ) (r, r, \dots, r) (r,r,...,r)）元素为 1，其余所有位置元素均为 0。
• 它的作用：在 Tucker 分解中，核心张量通常是稠密的。但是，如果我们将核心张量限制为这种"对角张量"，Tucker 分解就退化成了 CP 分解。这个 I N , R \boldsymbol{\mathcal{I}}{N,R} IN,R 的作用就是把各个因子矩阵 A ( n ) \mathbf{A}^{(n)} A(n) 中的对应列"挑选"出来并相乘，从而还原回公式 ( 2 ) (2) (2) 中的求和形式 ∑ r = 1 R \sum{r=1}^{R} ∑r=1R。>

Kruskal 算子表示法 = ⟦ A ( 1 ) , A ( 2 ) , ... , A ( N ) ⟧ = \llbracket \mathbf{A}^{(1)}, \mathbf{A}^{(2)}, \ldots, \mathbf{A}^{(N)} \rrbracket =[[A(1),A(2),...,A(N)]]

这是一个纯粹的数学简写符号，被称为 Kruskal 算子（Kruskal operator）。这组双括号 ⟦ ⋅ ⟧ \llbracket \cdot \rrbracket [[⋅]] 时，它的定义就是指代上述的 CP 分解模型。

其中算子 × n \times_n ×n 表示模- n n n 乘积。 X \boldsymbol{\mathcal{X}} X 的模- n n n 展开定义为 [31]

X ( n ) = ( A ( N ) ⊙ ⋯ A ( n + 1 ) ⊙ A ( n − 1 ) ⊙ ⋯ A ( 1 ) ) A ( n ) T ∈ C ( ∏ i ≠ n I i ) × I n . (3) \mathbf{X}{(n)} = \left( \mathbf{A}^{(N)} \odot \cdots \mathbf{A}^{(n+1)} \odot \mathbf{A}^{(n-1)} \odot \cdots \mathbf{A}^{(1)} \right) \mathbf{A}^{(n)\text{T}} \in \mathbb{C}^{(\prod{i \neq n} I_i) \times I_n}. \tag{3} X(n)=(A(N)⊙⋯A(n+1)⊙A(n−1)⊙⋯A(1))A(n)T∈C(∏i=nIi)×In.(3)

N N N 阶张量 X \boldsymbol{\mathcal{X}} X 的模- n n n 展开的向量化为

vec ( X ( n ) ) = ( A ( n ) ⊙ A ( N ) ⊙ ⋯ A ( n + 1 ) ⊙ A ( n − 1 ) ⊙ ⋯ A ( 1 ) ) 1 R . (4) \begin{aligned} &\text{vec} \left( \mathbf{X}_{(n)} \right) \\ &= \left( \mathbf{A}^{(n)} \odot \mathbf{A}^{(N)} \odot \cdots \mathbf{A}^{(n+1)} \odot \mathbf{A}^{(n-1)} \odot \cdots \mathbf{A}^{(1)} \right) \mathbf{1}_R. \end{aligned} \tag{4} vec(X(n))=(A(n)⊙A(N)⊙⋯A(n+1)⊙A(n−1)⊙⋯A(1))1R.(4)

模乘形式与 CP 分解等效性推导

1. 定义回顾

• 目标公式 (CPD) ：
  x i 1 i 2 ... i N = ∑ r = 1 R a i 1 r ( 1 ) a i 2 r ( 2 ) ⋯ a i N r ( N ) x_{i_1 i_2 \dots i_N} = \sum_{r=1}^{R} a^{(1)}{i_1 r} a^{(2)}{i_2 r} \cdots a^{(N)}_{i_N r} xi1i2...iN=r=1∑Rai1r(1)ai2r(2)⋯aiNr(N)
• 待推导公式 (模乘形式) ：
  X = I N , R × 1 A ( 1 ) × 2 A ( 2 ) ⋯ × N A ( N ) \boldsymbol{\mathcal{X}} = \boldsymbol{\mathcal{I}}_{N,R} \times_1 \mathbf{A}^{(1)} \times_2 \mathbf{A}^{(2)} \cdots \times_N \mathbf{A}^{(N)} X=IN,R×1A(1)×2A(2)⋯×NA(N)
• 核心张量性质 ： I N , R \boldsymbol{\mathcal{I}}{N,R} IN,R 为超对角张量，其元素满足：
  I r 1 r 2 ... r N = { 1 , 若 r 1 = r 2 = ⋯ = r N 0 , 其他情况 \mathcal{I}{r_1 r_2 \dots r_N} = \begin{cases} 1, & \text{若 } r_1 = r_2 = \dots = r_N \\ 0, & \text{其他情况} \end{cases} Ir1r2...rN={1,0,若 r1=r2=⋯=rN其他情况

2. 元素级推导

根据张量模乘（Tucker 分解）的通用定义， X \boldsymbol{\mathcal{X}} X 的元素由 N N N 重求和计算得出：
x i 1 i 2 ... i N = ∑ r 1 = 1 R ⋯ ∑ r N = 1 R I r 1 ... r N ⋅ ( a i 1 r 1 ( 1 ) ⋅ a i 2 r 2 ( 2 ) ⋯ a i N r N ( N ) ) x_{i_1 i_2 \dots i_N} = \sum_{r_1=1}^{R} \cdots \sum_{r_N=1}^{R} \mathcal{I}{r_1 \dots r_N} \cdot \left( a^{(1)}{i_1 r_1} \cdot a^{(2)}{i_2 r_2} \cdots a^{(N)}{i_N r_N} \right) xi1i2...iN=r1=1∑R⋯rN=1∑RIr1...rN⋅(ai1r1(1)⋅ai2r2(2)⋯aiNrN(N))

由于 I N , R \boldsymbol{\mathcal{I}}{N,R} IN,R 的对角特性 ，仅当 r 1 = r 2 = ⋯ = r N r_1 = r_2 = \dots = r_N r1=r2=⋯=rN （记为 r r r）时， I r 1 ... r N = 1 \mathcal{I}{r_1 \dots r_N} = 1 Ir1...rN=1，其余项均为 0。因此， N N N 重求和"坍缩"为对单一变量 r r r 的求和：
x i 1 i 2 ... i N = ∑ r = 1 R 1 ⋅ ( a i 1 r ( 1 ) ⋅ a i 2 r ( 2 ) ⋯ a i N r ( N ) ) = ∑ r = 1 R a i 1 r ( 1 ) a i 2 r ( 2 ) ⋯ a i N r ( N ) \begin{aligned} x_{i_1 i_2 \dots i_N} &= \sum_{r=1}^{R} 1 \cdot \left( a^{(1)}{i_1 r} \cdot a^{(2)}{i_2 r} \cdots a^{(N)}{i_N r} \right) \\ &= \sum{r=1}^{R} a^{(1)}{i_1 r} a^{(2)}{i_2 r} \cdots a^{(N)}_{i_N r} \end{aligned} xi1i2...iN=r=1∑R1⋅(ai1r(1)⋅ai2r(2)⋯aiNr(N))=r=1∑Rai1r(1)ai2r(2)⋯aiNr(N)
3. 结论

将上述标量形式还原为向量外积形式，即得 CP 分解公式：
X = ∑ r = 1 R a r ( 1 ) ∘ a r ( 2 ) ∘ ⋯ ∘ a r ( N ) \boldsymbol{\mathcal{X}} = \sum_{r=1}^{R} \mathbf{a}_r^{(1)} \circ \mathbf{a}_r^{(2)} \circ \cdots \circ \mathbf{a}_r^{(N)} X=r=1∑Rar(1)∘ar(2)∘⋯∘ar(N)

这证明了引入超对角核心张量 I N , R \boldsymbol{\mathcal{I}}_{N,R} IN,R 后，Tucker 形式即退化为 CP 分解。

公式 (4) 推导过程：张量展开的向量化

1. 基于公式 (3) 的简化表示

令 H \mathbf{H} H 为除 A ( n ) \mathbf{A}^{(n)} A(n) 以外其他因子矩阵的 Khatri-Rao 积：
H = A ( N ) ⊙ ⋯ ⊙ A ( n + 1 ) ⊙ A ( n − 1 ) ⊙ ⋯ ⊙ A ( 1 ) \mathbf{H} = \mathbf{A}^{(N)} \odot \cdots \odot \mathbf{A}^{(n+1)} \odot \mathbf{A}^{(n-1)} \odot \cdots \odot \mathbf{A}^{(1)} H=A(N)⊙⋯⊙A(n+1)⊙A(n−1)⊙⋯⊙A(1)

则公式 (3) 可写为两个矩阵的乘积，即 R R R 个秩-1 矩阵的求和：
X ( n ) = H A ( n ) T = ∑ r = 1 R h r a r ( n ) T \mathbf{X}{(n)} = \mathbf{H} \mathbf{A}^{(n)\text{T}} = \sum{r=1}^{R} \mathbf{h}_r \mathbf{a}_r^{(n)\text{T}} X(n)=HA(n)T=r=1∑Rhrar(n)T

其中 h r \mathbf{h}_r hr 和 a r ( n ) \mathbf{a}_r^{(n)} ar(n) 分别是矩阵 H \mathbf{H} H 和 A ( n ) \mathbf{A}^{(n)} A(n) 的第 r r r 列。
2. 向量化运算 (Vectorization)

对上式两边进行向量化，并利用性质 vec ( u v T ) = v ⊗ u \text{vec}(\mathbf{u}\mathbf{v}^{\text{T}}) = \mathbf{v} \otimes \mathbf{u} vec(uvT)=v⊗u：
vec ( X ( n ) ) = ∑ r = 1 R vec ( h r a r ( n ) T ) = ∑ r = 1 R ( a r ( n ) ⊗ h r ) \begin{aligned} \text{vec}\left( \mathbf{X}{(n)} \right) &= \sum{r=1}^{R} \text{vec}\left( \mathbf{h}_r \mathbf{a}r^{(n)\text{T}} \right) \\ &= \sum{r=1}^{R} \left( \mathbf{a}_r^{(n)} \otimes \mathbf{h}_r \right) \end{aligned} vec(X(n))=r=1∑Rvec(hrar(n)T)=r=1∑R(ar(n)⊗hr)
3. 利用 Khatri-Rao 积的定义

上式中的项 a r ( n ) ⊗ h r \mathbf{a}_r^{(n)} \otimes \mathbf{h}_r ar(n)⊗hr 恰好是以下大矩阵的第 r r r 列：
M = A ( n ) ⊙ H = A ( n ) ⊙ A ( N ) ⊙ ⋯ ⊙ A ( 1 ) \mathbf{M} = \mathbf{A}^{(n)} \odot \mathbf{H} = \mathbf{A}^{(n)} \odot \mathbf{A}^{(N)} \odot \cdots \odot \mathbf{A}^{(1)} M=A(n)⊙H=A(n)⊙A(N)⊙⋯⊙A(1)

由于将矩阵的所有列相加等价于该矩阵右乘全 1 向量 1 R \mathbf{1}R 1R，即 ∑ r = 1 R m r = M 1 R \sum{r=1}^{R} \mathbf{m}_r = \mathbf{M} \mathbf{1}R ∑r=1Rmr=M1R，故得证：
vec ( X ( n ) ) = ( A ( n ) ⊙ A ( N ) ⊙ ⋯ ⊙ A ( 1 ) ) 1 R \text{vec} \left( \mathbf{X}{(n)} \right) = \left( \mathbf{A}^{(n)} \odot \mathbf{A}^{(N)} \odot \cdots \odot \mathbf{A}^{(1)} \right) \mathbf{1}_R vec(X(n))=(A(n)⊙A(N)⊙⋯⊙A(1))1R

III. SYSTEM MODEL

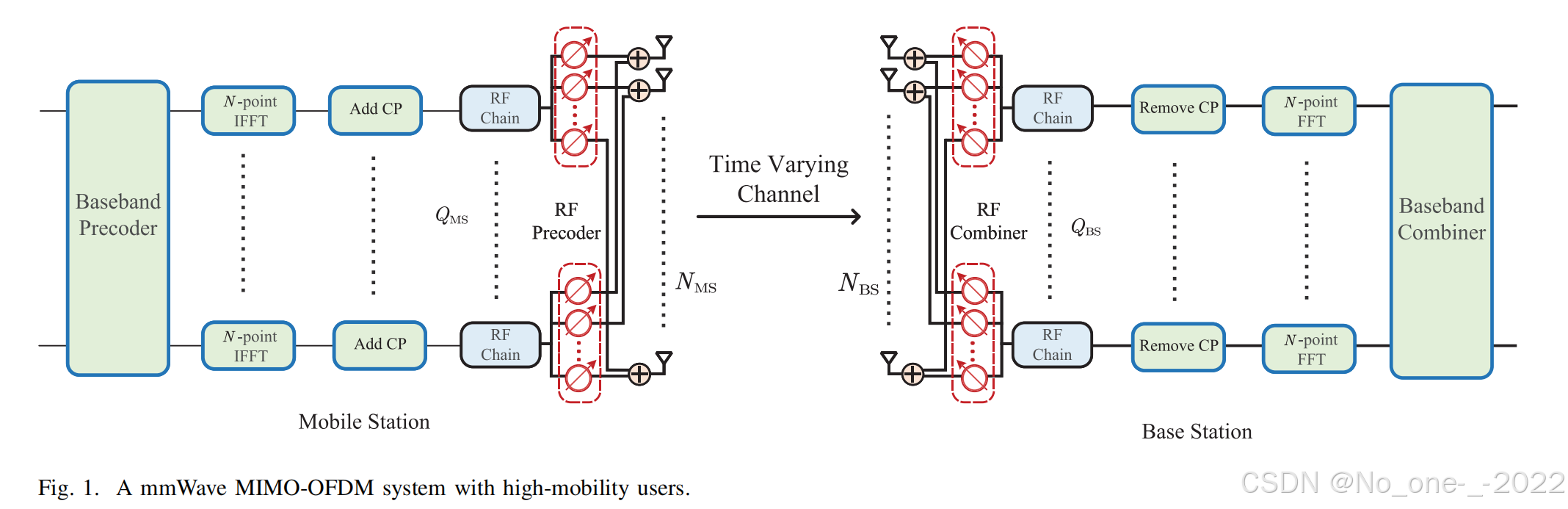
考虑如图 1 所示的上行链路毫米波大规模 MIMO-OFDM 系统，其包含一个基站 (BS) 和一个移动台 (MS)。BS 配备 N BS N_{\text{BS}} NBS 根天线和 Q BS Q_{\text{BS}} QBS 个射频 (RF) 链路，而 MS 配备 N MS N_{\text{MS}} NMS 根天线和 Q MS Q_{\text{MS}} QMS 个 RF 链路。BS 和 MS 均采用均匀线性阵列 (ULA)。不失一般性，我们假设 RF 链路的数量小于天线数量，即 Q MS < N MS Q_{\text{MS}} < N_{\text{MS}} QMS<NMS 和 Q BS < N BS Q_{\text{BS}} < N_{\text{BS}} QBS<NBS。OFDM 子载波总数为 N N N，其中 K K K 个子载波被选择用于信道估计。在接下来的部分中，我们重点讨论单用户情况。通过为不同用户分配不同的带宽部分 (BWP) 并在单独的子载波集上执行信道估计，可以实现到多用户情况的扩展。

假设 BS 和 MS 之间存在 L L L 条传播路径，则时域和时延域中的信道矩阵由下式给出

H [ t , τ ] = ∑ l = 1 L α l e j 2 π f l d t a N BS ( θ l ) a N MS T ( ϕ l ) δ ( τ − τ l ) , (5) \mathbf{H} [t, \tau] = \sum_{l=1}^{L} \alpha_l e^{j2\pi f_l^d t} \mathbf{a}{N{\text{BS}}} (\theta_l) \mathbf{a}{N{\text{MS}}}^{\text{T}} (\phi_l) \delta (\tau - \tau_l), \tag{5} H[t,τ]=l=1∑Lαlej2πfldtaNBS(θl)aNMST(ϕl)δ(τ−τl),(5)

其中 t t t 和 τ \tau τ 分别表示连续时域和时延域中的尺度， α l \alpha_l αl 表示服从复高斯分布的复信道增益， f l d f_l^d fld 表示第 l l l 条路径的多普勒频率， θ l \theta_l θl 和 ϕ l \phi_l ϕl 分别表示第 l l l 条路径的到达角 (AoA) 和离开角 (AoD)， τ l \tau_l τl 表示第 l l l 条路径的传播时延。此外， a N BS ( ⋅ ) \mathbf{a}{N{\text{BS}}}(\cdot) aNBS(⋅) 和 a N MS ( ⋅ ) \mathbf{a}{N{\text{MS}}}(\cdot) aNMS(⋅) 分别表示 BS 和 MS 的阵列导向矢量。对于简单的 ULA，阵列导向矢量 a X ( x ) ∈ C X × 1 \mathbf{a}_X(x) \in \mathbb{C}^{X \times 1} aX(x)∈CX×1 表示为

a X ( x ) = [ 1 , e − j 2 π d λ c cos ⁡ ( x ) , ... , e − j 2 π ( X − 1 ) d λ c cos ⁡ ( x ) ] T , (6) \mathbf{a}_X (x) = \left[ 1, e^{-j2\pi \frac{d}{\lambda_c} \cos(x)}, \ldots, e^{-j2\pi (X-1) \frac{d}{\lambda_c} \cos(x)} \right]^{\text{T}}, \tag{6} aX(x)=[1,e−j2πλcdcos(x),...,e−j2π(X−1)λcdcos(x)]T,(6)

其中 d d d 是天线间距， λ c \lambda_c λc 是载波波长， x x x 表示角度（分别是 BS 处的 AoA 和 MS 处的 AoD）。假设每种类型的 ULA 中的天线间距满足 d = λ c / 2 d = \lambda_c/2 d=λc/2。

B. Proposed Transmission Structure Based on 5G NR

在毫米波系统中，多普勒频率导致信道相干时间比 6 GHz 以下 (sub-6 GHz) 系统更短 [32]。先前的研究 [18], [19], [22], [23] 和 [24] 通常在每一帧的初始时隙中插入导频信号以估计角度信息，并在随后的所有时隙中更新信道增益。这种导频方案有两个主要缺点：

1. 由于需要在每个时隙中都有导频符号，它引入了相当大的开销；
2. 由于需要在整个帧中重复进行信道增益估计，它增加了系统复杂度。

在车载通信中，移动台 (MS) 在 10 ms 帧内的移动保持大尺度信道参数（例如，角度、时延、路径损耗）几乎恒定。因此，导频被部署在初始时隙中以估计角度、增益、时延和多普勒频率等参数，从而为数据传输预留后续时隙。此外，毫米波频段中较高的多普勒频率使得 sub-6G 系统的 15 kHz 子载波间隔不再适用，原因是信道变化迅速且多普勒估计的分辨率降低。

信道的相干时间（ T c T_c Tc）通常近似为最大多普勒频移（ f d f_{d} fd），这意味着15kHz 子载波间隔的OFDM符号时间长度太长了，信道变化的更快。

幸运的是，5G NR 支持多种 OFDM 参数配置，其子载波间隔 (SCS) 为 2 μ ⋅ 15 2^\mu \cdot 15 2μ⋅15 kHz，其中 μ \mu μ 在毫米波频段的取值范围为 0 到 6 [26]。考虑将一个时隙内的 N s = 6 N_{\text{s}} = 6 Ns=6 个连续 OFDM 符号组合成一个用于导频传输的迷你时隙 (mini-slot)，如图 2 所示。对于 μ = 5 \mu = 5 μ=5，SCS 为 480 kHz，产生的迷你时隙持续时间为 12.5 μ s \mu\text{s} μs。给定 30 m/s 的车辆速度和 30 GHz 的载波频率，相干时间为 333.3 μ s \mu\text{s} μs。因此，假设信道在这样一个迷你时隙期间保持不变，且信道参数（角度、时延、多普勒频率）在几个时隙内保持恒定，是合理的。

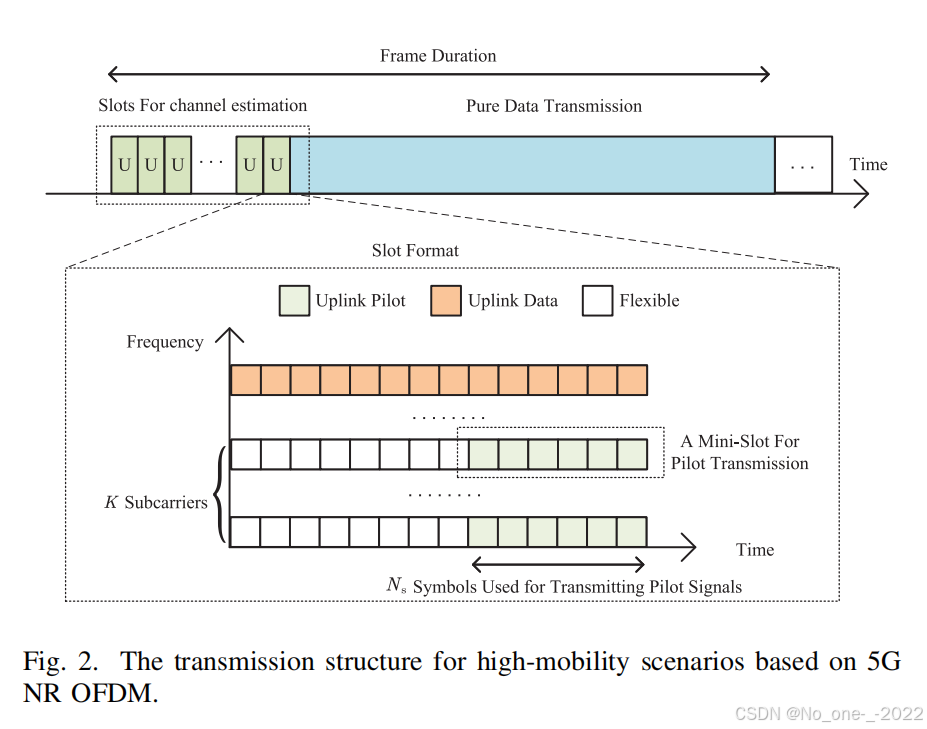
基于 5G NR，我们针对高移动性场景提出了一种新型传输结构，如图 2 所示。在该结构中，一帧的前 M M M 个时隙被分配用于上行链路业务，其中 K K K 个子载波使用时隙格式 (Slot Format) 45 [26] 传输导频信号，其中每个时隙的最后 6 个 OFDM 符号构成一个用于上行链路导频传输的迷你时隙。剩余的时隙完全用于上行链路或下行链路数据传输，利用从前 M M M 个时隙估计出的 CSI。与现有的传输结构相比，所提出的方案消除了在每个时隙更新信道信息的需要，从而显著降低了系统复杂度。

C. Signal Model