
本MATLAB 代码实现了一个经典的二维雷达目标跟踪系统 ,采用扩展卡尔曼滤波 (EKF) 算法处理雷达的非线性观测数据(距离和角度)。
文章目录
程序详解
项目概述
本代码仿真了一个单一雷达站对二维平面内机动目标进行探测与跟踪的场景。由于雷达的观测数据为极坐标系下的距离 (Range) 和 方位角 (Azimuth) ,与目标在笛卡尔坐标系下的运动方程存在非线性关系,因此代码采用了扩展卡尔曼滤波 (Extended Kalman Filter, EKF) 进行状态估计。
该仿真不仅实现了滤波算法,还引入了纯惯导推算作为对比,直观展示了多源数据融合(EKF)在消除累积误差和观测噪声方面的优势。
代码功能亮点
- 多维度对比分析 :
- 真实轨迹:目标的实际运动路径(含加速度)。
- 雷达原始观测:将带噪声的极坐标测量值直接转换为直角坐标,展示原始测量的离散性。
- 纯惯导 (Inertial):仅靠初始状态推算,展示无观测修正时的误差累积(漂移)现象。
- EKF 估计:融合预测与观测,输出平滑且高精度的轨迹。
- 定量的误差评估 :
- 自动计算平均误差 (Mean Error) 和 均方根误差 (RMSE)。
- 量化展示 EKF 相比于原始观测和纯惯导的性能提升百分比。
- 丰富的可视化输出 :
- 轨迹图:直观展示四种轨迹的几何关系。
- 误差曲线图:随时间变化的误差波动。
- 统计柱状图:清晰对比三种方法的整体精度。
运行结果分析
- 轨迹图:纯惯导轨迹会随着时间推移逐渐偏离真实轨迹(漂移);雷达原始观测点围绕真实轨迹抖动;而 EKF 轨迹紧密跟随真实目标,且比原始观测更平滑。
- 误差曲线:纯惯导的误差呈发散趋势(越来越大),而 EKF 的误差会收敛在一个较小的稳定范围内。
- 性能指标:控制台输出将显示 EKF 的 RMSE 显著低于雷达观测噪声和惯导误差。
运行结果
轨迹曲线,同时标注了雷达的位置:
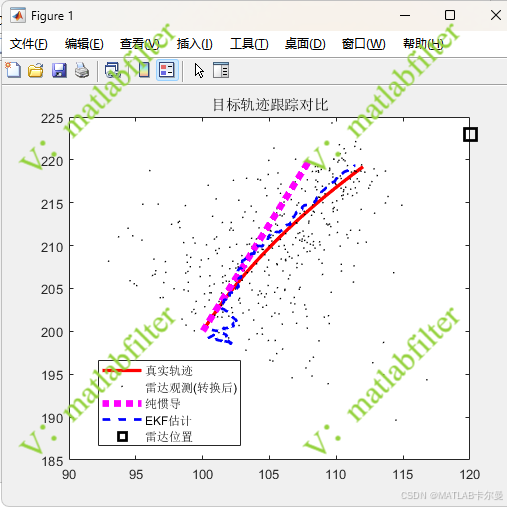
误差曲线对比:

命令行输出的仿真结果:
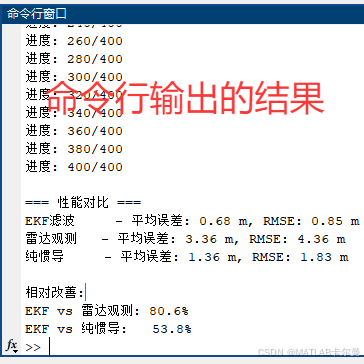
MATLAB源代码
部分代码如下:
matlab
% 雷达测角测距定位-二维-单一雷达,轨迹用EKF,观测为距离和角度
% 作者:matlabfilter
% 2025-11-25/Ver1
clear; close all; clc;
rng(0);
%% 参数设置
dt = 0.01;
N = 400;
target_position = [100; 200];
target_velocity = [2; 5];
target_acceleration = [0.5; -0.1];
radar_position = [120; 223];
range_noise_std = 1;
angle_noise_std = 0.2;
%% EKF 状态模型
F = [1 0 dt 0;
0 1 0 dt;
0 0 1 0;
0 0 0 1];
q = 0.1;
Q = q * [dt^4/4 0 dt^3/2 0;
0 dt^4/4 0 dt^3/2;
dt^3/2 0 dt^2 0;
0 dt^3/2 0 dt^2];
% 测量噪声(r, theta)
R = diag([range_noise_std^2, angle_noise_std^2]);
% 初始状态估计
x_est = [target_position; target_velocity];
P = diag([3 3 0.5 0.5]);
%% 纯惯导
inertial_position = target_position;
inertial_velocity = target_velocity;
%% 数据存储
true_positions = zeros(N, 2);
true_velocities = zeros(N, 2);
measurements_xy = zeros(N, 2); % 仅用于绘图
estimated_positions = zeros(N, 2);
estimated_velocities = zeros(N, 2);
inertial_positions = zeros(N, 2);
inertial_velocities = zeros(N, 2);
fprintf('开始 EKF 雷达跟踪仿真...\n');
for i = 1:N
%% ===== 真实目标运动 =====
target_position = target_position + target_velocity * dt + 0.5 * target_acceleration * dt^2;完整代码:https://download.csdn.net/download/callmeup/92408480
或:
如需帮助,或有导航、定位滤波相关的代码定制需求,请点击下方卡片联系作者