【算法基础篇】（二十三）数据结构之并查集基础：从原理到实战，一篇吃透！

目录

前言

一、铺垫：什么是双亲表示法？

[二、并查集的核心概念：维护集合的 "神器"](#二、并查集的核心概念：维护集合的 “神器”)

[2.1 并查集解决什么问题？](#2.1 并查集解决什么问题？)

[2.2 并查集的本质：森林结构](#2.2 并查集的本质：森林结构)

[三、并查集的基础实现：从 0 到 1 写代码](#三、并查集的基础实现：从 0 到 1 写代码)

[3.1 初始化（Init）](#3.1 初始化（Init）)

[3.2 查询操作（Find）](#3.2 查询操作（Find）)

[3.3 合并操作（Union）](#3.3 合并操作（Union）)

[3.4 判断操作（IsSame）](#3.4 判断操作（IsSame）)

[3.5 基础实现完整示例](#3.5 基础实现完整示例)

[四、并查集的优化：从 O (n) 到近乎 O (1)](#四、并查集的优化：从 O (n) 到近乎 O (1))

[4.1 路径压缩：查询时 "扁平化" 树结构](#4.1 路径压缩：查询时 “扁平化” 树结构)

[4.2 按秩合并（可选优化）](#4.2 按秩合并（可选优化）)

五、普通并查集的经典实战：从模板题到应用题

[5.1 【模板题】洛谷 P3367 并查集](#5.1 【模板题】洛谷 P3367 并查集)

题目描述

解题思路

完整代码

[5.2 【应用题】洛谷 P1551 亲戚](#5.2 【应用题】洛谷 P1551 亲戚)

题目描述

解题思路

完整代码

[5.3 【应用题】洛谷 P1596 Lake Counting（水坑计数）](#5.3 【应用题】洛谷 P1596 Lake Counting（水坑计数）)

题目描述

解题思路

完整代码

[5.4 【进阶题】洛谷 P1955 程序自动分析](#5.4 【进阶题】洛谷 P1955 程序自动分析)

题目描述

解题思路

完整代码

六、总结：并查集的核心与拓展

[6.1 核心要点](#6.1 核心要点)

[6.2 拓展方向](#6.2 拓展方向)

[6.3 学习建议](#6.3 学习建议)

总结

---

前言

在算法竞赛和日常开发中，我们经常会遇到一类问题：需要频繁维护多个元素的集合关系，比如判断两个元素是否属于同一集合、将两个集合合并。如果用普通的数组或链表来实现，效率往往不尽如人意。而并查集（Union Find） 作为一种专门解决这类问题的数据结构，凭借近乎 O (1) 的操作效率，成为了程序员的 "必备利器"。

今天这篇文章，我会从最基础的双亲表示法讲起，一步步拆解并查集的概念、实现、优化，再结合经典例题实战，保证让你从 "小白" 到 "精通"，彻底吃透并查集！下面就让我们正式开始吧！

---

一、铺垫：什么是双亲表示法？

在正式讲并查集之前，我们先聊聊双亲表示法------ 因为并查集的本质，就是用双亲表示法实现的森林。

学过树结构的同学都知道，树的存储方式有很多：孩子表示法、双亲表示法、孩子双亲表示法、孩子兄弟表示法等。其中双亲表示法的核心思路特别简单：除了根节点，树中每个节点都有且仅有一个父节点，我们只需要用数组记录每个节点的父节点编号即可。

举个例子，假设有这样一棵简单的树：

        1
    /   |   \
    2   3    4
   / \       |
  5   6      7
            /|\
           8 9 10

用双亲表示法存储时，我们可以定义一个数组fa（father 的缩写），数组下标代表节点编号，数组值代表该节点的父节点编号：

节点下标	1	2	3	4	5	6
fa [下标]	-1	1	1	3	2	2

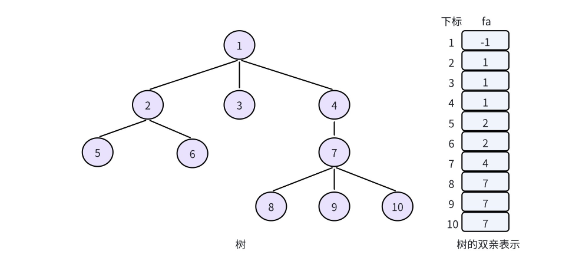
这里根节点 1 的父节点标记为 - 1（表示没有父节点），节点 2 的父节点是 1，节点 5 的父节点是 2，以此类推。

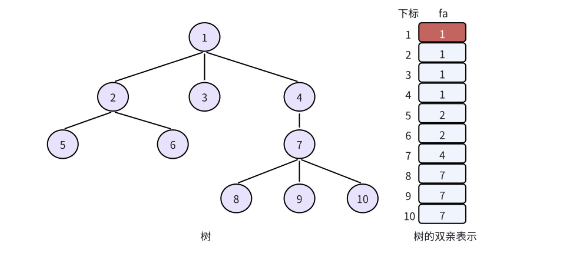
不过在并查集的实现中，我们会做一点小调整：让根节点的父节点指向自己，这样上面的数组就变成了：

节点下标	1	2	3	4	5	6
fa [下标]	1	1	1	3	2	2

这个小调整看似不起眼，却能极大简化后续的查询和合并操作 ------ 这也是并查集实现的关键铺垫。

二、并查集的核心概念：维护集合的 "神器"

2.1 并查集解决什么问题？

先想一个场景：有 10 个小朋友，一开始每个人都是一个独立的小团体。接下来会发生两种操作：

1. 把小朋友 A 和小朋友 B 的团体合并成一个大团体；
2. 问小朋友 C 和小朋友 D 是不是在同一个团体里。

如果用普通方法（比如遍历），每次合并 / 查询都要扫一遍所有元素，效率极低。而并查集就是为这类 "动态维护集合关系" 的问题而生的，它能高效支持以下三种核心操作：

• 查询（Find）：查找某个元素属于哪个集合（通常返回集合的 "代表元素"，也就是根节点）；
• 合并（Union）：将两个元素所在的集合合并成一个集合；
• 判断（IsSame）：判断两个元素是否在同一个集合中（本质是查询两个元素的根节点是否相同）。

2.2 并查集的本质：森林结构

并查集的底层实现是森林------ 每一棵树代表一个集合，树的每个节点对应集合中的一个元素，树的根节点就是这个集合的 "代表"。

比如有三个集合：{1,2,5,6}、{3,4}、{7,8,9}，对应的森林结构如下：

树1：1 -> 2 -> 5, 1 -> 2 -> 6, 1 -> 3 -> 4
树2：7 -> 8 -> 9

（注：箭头表示父节点指向，根节点 1 的父节点是自己，根节点 7 的父节点是自己）

又如如下的结构：

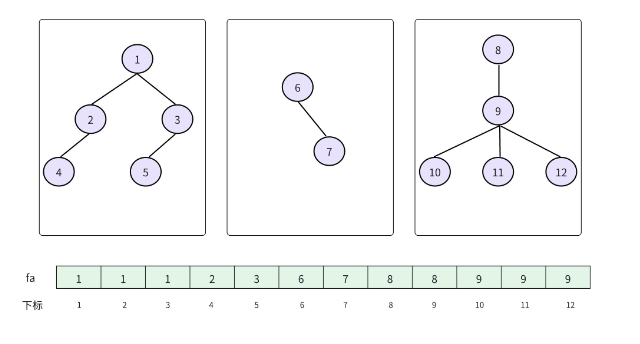
通过这种结构，我们可以快速定位每个元素的 "归属"，进而完成合并和查询。

三、并查集的基础实现：从 0 到 1 写代码

接下来我们用 C++ 实现最基础的并查集，核心分为四步：初始化、查询、合并、判断。

3.1 初始化（Init）

初始状态下，每个元素都是一个独立的集合，因此每个元素的父节点都是自己。

#include <iostream>
using namespace std;

const int N = 1e6 + 10; // 根据题目需求调整数组大小
int fa[N]; // 存储每个节点的父节点
int n;     // 元素总数

// 初始化并查集
void init() {
    for (int i = 1; i <= n; i++) {
        fa[i] = i; // 每个元素的父节点指向自己
    }
}

3.2 查询操作（Find）

查询操作是并查集的核心，目标是找到某个元素所在集合的根节点。思路很简单：一直向上找父节点，直到找到父节点是自己的节点（根节点）。

// 查找元素x的根节点（基础版，无优化）
int find(int x) {
    if (fa[x] == x) { // 找到根节点
        return x;
    }
    return find(fa[x]); // 递归找父节点
}

// 一行简化版
// int find(int x) {
//     return fa[x] == x ? x : find(fa[x]);
// }

举个例子：如果要找节点 5 的根节点，过程是：fa[5]=2 → fa[2]=1 → fa[1]=1，最终返回 1，说明 5 属于根节点 1 的集合。

3.3 合并操作（Union）

合并操作的目标是将两个元素所在的集合合并。核心思路：找到两个元素的根节点，让其中一个根节点的父节点指向另一个根节点（谁指向谁都可以，基础版无需纠结）。

注意：C++ 中union是关键字，因此函数名不能用union，这里用un代替。

// 合并元素x和y所在的集合
void un(int x, int y) {
    int fx = find(x); // 找到x的根节点
    int fy = find(y); // 找到y的根节点
    if (fx != fy) {   // 不在同一个集合才需要合并
        fa[fx] = fy;  // 让x的根节点指向y的根节点
    }
}

比如合并节点 5 和节点 4：

• find(5)=1，find(4)=3；
• 执行fa[1] = 3，此时根节点 1 的父节点变成 3，两个集合合并为 {1,2,3,4,5,6}。

3.4 判断操作（IsSame）

判断两个元素是否在同一个集合，只需要看它们的根节点是否相同即可：

// 判断元素x和y是否在同一个集合
bool issame(int x, int y) {
    return find(x) == find(y);
}

3.5 基础实现完整示例

把上面的代码整合起来，就是一个完整的基础并查集：

#include <iostream>
using namespace std;

const int N = 1e6 + 10;
int fa[N];
int n;

// 初始化
void init() {
    for (int i = 1; i <= n; i++) {
        fa[i] = i;
    }
}

// 查询根节点（基础版）
int find(int x) {
    return fa[x] == x ? x : find(fa[x]);
}

// 合并集合
void un(int x, int y) {
    int fx = find(x);
    int fy = find(y);
    if (fx != fy) {
        fa[fx] = fy;
    }
}

// 判断是否同集合
bool issame(int x, int y) {
    return find(x) == find(y);
}

// 测试示例
int main() {
    n = 6;
    init(); // 初始化6个元素
    
    // 合并操作
    un(2, 1);
    un(5, 2);
    un(6, 2);
    un(4, 3);
    
    // 查询测试
    cout << "5和4是否同集合：" << (issame(5,4) ? "是" : "否") << endl; // 否
    un(1, 3); // 合并1和3的集合
    cout << "5和4是否同集合：" << (issame(5,4) ? "是" : "否") << endl; // 是
    
    return 0;
}

运行结果：

5和4是否同集合：否
5和4是否同集合：是

四、并查集的优化：从 O (n) 到近乎 O (1)

基础版并查集虽然能工作，但在极端情况下效率会很低 ------ 比如合并操作让树退化成链表，此时查询操作的时间复杂度会变成 O (n)。

比如连续执行un(2,1)、un(3,2)、un(4,3)、un(5,4)，树会变成：1 ← 2 ← 3 ← 4 ← 5，此时查询 find (5) 需要递归 5 次。

为了解决这个问题，我们需要对并查集进行优化，最核心的优化是路径压缩 ，其次是可选的按秩合并。

4.1 路径压缩：查询时 "扁平化" 树结构

路径压缩的核心思想：在查询某个节点的根节点时，把该节点到根节点路径上的所有节点的父节点都直接指向根节点。这样下次查询时，就能直接找到根节点，极大减少递归次数。

修改后的 find 函数：

// 查找根节点（带路径压缩）
int find(int x) {
    if (fa[x] == x) {
        return x;
    }
    // 路径压缩：将x的父节点直接设为根节点
    return fa[x] = find(fa[x]);
}

// 一行简化版
// int find(int x) {
//     return fa[x] == x ? x : fa[x] = find(fa[x]);
// }

还是以链表状的树1 ← 2 ← 3 ← 4 ← 5为例：

• 第一次调用 find (5) 时，递归找到根节点 1；
• 同时执行fa[5]=1、fa[4]=1、fa[3]=1、fa[2]=1；
• 下次再调用 find (5)，直接返回 1，无需递归。

路径压缩后，查询操作的时间复杂度会骤降。《算法导论》中证明，带路径压缩的并查集查询的最坏时间复杂度为O (α(n)) ，其中α(n) 是阿克曼函数的反函数 ------ 这是一个增长极慢的函数，对于 n≤10^600 的情况，α(n) 都不超过 5，因此可以近似认为是 O (1)。

4.2 按秩合并（可选优化）

除了路径压缩，还有一种优化方式是 "按秩合并"------ 所谓 "秩"，可以是树的高 度，也可以是树的大小。合并时，让 "秩" 小的树的根节点指向 "秩" 大的树的根节点，避免树的高度不必要地增加。

比如我们用rank[]数组记录每个树的高度，初始化时rank[i]=1（每个树只有一个节点，高度为 1）：

int rank[N]; // 记录每个根节点对应树的高度

// 初始化
void init() {
    for (int i = 1; i <= n; i++) {
        fa[i] = i;
        rank[i] = 1; // 初始高度为1
    }
}

// 合并（按秩合并）
void un(int x, int y) {
    int fx = find(x);
    int fy = find(y);
    if (fx == fy) return;
    // 让高度小的树合并到高度大的树下
    if (rank[fx] < rank[fy]) {
        fa[fx] = fy;
    } else {
        fa[fy] = fx;
        // 如果高度相同，合并后高度+1
        if (rank[fx] == rank[fy]) {
            rank[fx]++;
        }
    }
}

按秩合并可以进一步降低树的高度，但实际开发中，仅用路径压缩就足以让并查集的效率达到近乎 O (1)，因此很多场景下可以不用按秩合并。

五、普通并查集的经典实战：从模板题到应用题

光说不练假把式，接下来我们结合几道经典例题，看看并查集在实际问题中的应用。

5.1 【模板题】洛谷 P3367 并查集

题目描述

题目链接如下：https://www.luogu.com.cn/problem/P3367

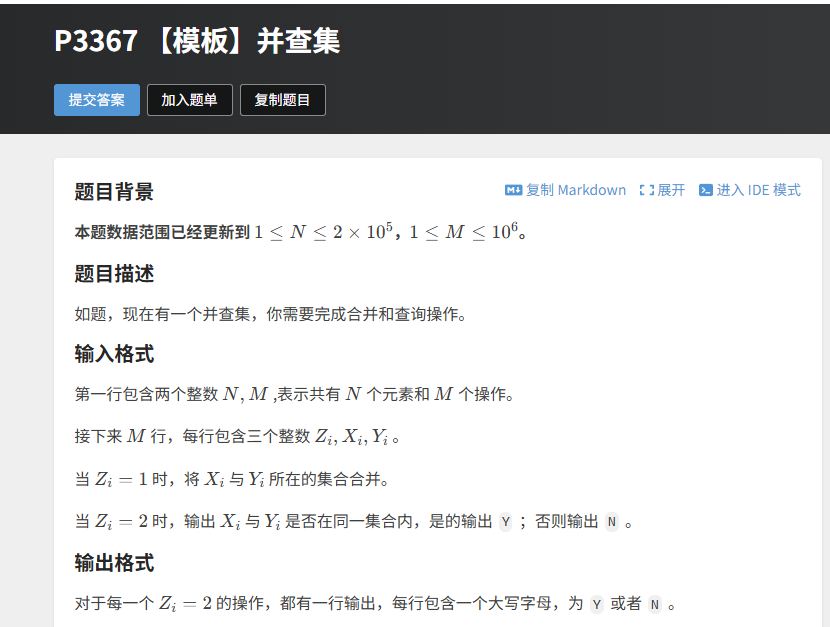
给定 N 个元素和 M 个操作，操作分为两种：

1. 1 X Y：将 X 和 Y 所在的集合合并；
2. 2 X Y：查询 X 和 Y 是否在同一个集合中，是则输出 Y，否则输出 N。

解题思路

纯模板题，直接用带路径压缩的并查集实现即可。

完整代码

#include <iostream>
using namespace std;

const int N = 2e5 + 10;
int fa[N];
int n, m;

// 带路径压缩的查询
int find(int x) {
    return fa[x] == x ? x : fa[x] = find(fa[x]);
}

// 合并操作
void un(int x, int y) {
    int fx = find(x);
    int fy = find(y);
    if (fx != fy) {
        fa[fx] = fy;
    }
}

int main() {
    cin >> n >> m;
    // 初始化
    for (int i = 1; i <= n; i++) {
        fa[i] = i;
    }
    
    while (m--) {
        int op, x, y;
        cin >> op >> x >> y;
        if (op == 1) {
            un(x, y);
        } else {
            if (find(x) == find(y)) {
                cout << "Y" << endl;
            } else {
                cout << "N" << endl;
            }
        }
    }
    
    return 0;
}

5.2 【应用题】洛谷 P1551 亲戚

题目链接：https://www.luogu.com.cn/problem/P1551

题目描述

规定：如果 A 和 B 是亲戚，B 和 C 是亲戚，那么 A 和 C 也是亲戚。给定 n 个人、m 个亲戚关系、p 个查询，每个查询问两个人是否是亲戚。

解题思路

亲戚关系是典型的 "等价关系"（自反、对称、传递），可以用并查集维护：

• 初始化：每个人是独立集合；
• 遍历 m 个亲戚关系，合并对应的两个人；
• 遍历 p 个查询，判断两个人是否同集合。

完整代码

#include <iostream>
using namespace std;

const int N = 5010;
int fa[N];
int n, m, p;

int find(int x) {
    return fa[x] == x ? x : fa[x] = find(fa[x]);
}

void un(int x, int y) {
    int fx = find(x);
    int fy = find(y);
    if (fx != fy) {
        fa[fy] = fx;
    }
}

bool issame(int x, int y) {
    return find(x) == find(y);
}

int main() {
    cin >> n >> m >> p;
    // 初始化
    for (int i = 1; i <= n; i++) {
        fa[i] = i;
    }
    
    // 处理亲戚关系
    while (m--) {
        int x, y;
        cin >> x >> y;
        un(x, y);
    }
    
    // 处理查询
    while (p--) {
        int x, y;
        cin >> x >> y;
        if (issame(x, y)) {
            cout << "Yes" << endl;
        } else {
            cout << "No" << endl;
        }
    }
    
    return 0;
}

5.3 【应用题】洛谷 P1596 Lake Counting（水坑计数）

题目链接：https://www.luogu.com.cn/problem/P1596

题目描述

用 N×M 的网格表示田地，W 表示水，. 表示旱地。相邻（8 个方向）的 W 视为一个水坑，求水坑的总数。

解题思路

将每个 W 视为一个元素，把相邻的 W 合并到同一个集合中，最终统计有多少个独立的集合（根节点是自己的 W）。

注意：需要将二维网格的坐标转换为一维下标（比如 (i,j) → i×M + j），方便用数组存储父节点。

完整代码

#include <iostream>
using namespace std;

const int N = 110;
char a[N][N];
int fa[N * N]; // 二维转一维：i*M + j
int n, m;

// 8个方向中的4个（避免重复合并，选右、下、右下、左下即可）
int dx[] = {0, 1, 1, 1};
int dy[] = {1, 1, 0, -1};

int find(int x) {
    return fa[x] == x ? x : fa[x] = find(fa[x]);
}

void un(int x, int y) {
    fa[find(x)] = find(y);
}

int main() {
    cin >> n >> m;
    for (int i = 0; i < n; i++) {
        cin >> a[i];
    }
    
    // 初始化并查集
    for (int i = 0; i < n * m; i++) {
        fa[i] = i;
    }
    
    // 遍历网格，合并相邻的W
    for (int i = 0; i < n; i++) {
        for (int j = 0; j < m; j++) {
            if (a[i][j] == '.') continue; // 旱地跳过
            int idx = i * m + j; // 二维转一维
            // 检查4个方向
            for (int k = 0; k < 4; k++) {
                int x = i + dx[k];
                int y = j + dy[k];
                // 边界判断
                if (x >= 0 && x < n && y >= 0 && y < m && a[x][y] == 'W') {
                    int nidx = x * m + y;
                    un(idx, nidx);
                }
            }
        }
    }
    
    // 统计独立的水坑（根节点是自己的W）
    int cnt = 0;
    for (int i = 0; i < n * m; i++) {
        int x = i / m;
        int y = i % m;
        if (a[x][y] == 'W' && fa[i] == i) {
            cnt++;
        }
    }
    
    cout << cnt << endl;
    return 0;
}

5.4 【进阶题】洛谷 P1955 程序自动分析

题目链接：https://www.luogu.com.cn/problem/P1955

题目描述

给定 n 个约束条件（x=y 或 x≠y），判断这些条件是否能同时满足。

解题思路

1. 先处理所有 x=y 的条件，用并查集合并 x 和 y；
2. 再处理所有 x≠y 的条件，若 x 和 y 在同一个集合中，则条件冲突，返回 NO；
3. 注意：x 和 y 的取值范围可能很大（比如 1e9），需要先离散化（将大数值映射为小下标）。

完整代码

#include <iostream>
#include <unordered_map>
#include <algorithm>
using namespace std;

const int N = 1e5 + 10;
struct Node {
    int x, y, e; // e=1表示x=y，e=0表示x≠y
} a[N];

// 离散化相关
int disc[N * 2];
unordered_map<int, int> mp;
int pos, cnt;

// 并查集相关
int fa[N * 2];

int find(int x) {
    return fa[x] == x ? x : fa[x] = find(fa[x]);
}

void un(int x, int y) {
    fa[find(x)] = find(y);
}

bool issame(int x, int y) {
    return find(x) == find(y);
}

bool solve() {
    int n;
    cin >> n;
    pos = 0;
    mp.clear();
    
    // 收集所有需要离散化的数值
    for (int i = 1; i <= n; i++) {
        cin >> a[i].x >> a[i].y >> a[i].e;
        disc[++pos] = a[i].x;
        disc[++pos] = a[i].y;
    }
    
    // 离散化：排序+去重+映射
    sort(disc + 1, disc + 1 + pos);
    cnt = 0;
    for (int i = 1; i <= pos; i++) {
        if (mp.count(disc[i])) continue;
        mp[disc[i]] = ++cnt;
    }
    
    // 初始化并查集
    for (int i = 1; i <= cnt; i++) {
        fa[i] = i;
    }
    
    // 处理x=y的条件
    for (int i = 1; i <= n; i++) {
        if (a[i].e == 1) {
            int x = mp[a[i].x];
            int y = mp[a[i].y];
            un(x, y);
        }
    }
    
    // 处理x≠y的条件
    for (int i = 1; i <= n; i++) {
        if (a[i].e == 0) {
            int x = mp[a[i].x];
            int y = mp[a[i].y];
            if (issame(x, y)) {
                return false;
            }
        }
    }
    
    return true;
}

int main() {
    int T;
    cin >> T;
    while (T--) {
        if (solve()) {
            cout << "YES" << endl;
        } else {
            cout << "NO" << endl;
        }
    }
    return 0;
}

六、总结：并查集的核心与拓展

6.1 核心要点

1. 并查集的本质是用森林维护集合关系，根节点是集合的代表；
2. 核心操作：初始化、查询（Find）、合并（Union）、判断（IsSame）；
3. 优化关键：路径压缩（必选）+ 按秩合并（可选），效率近乎 O (1)；
4. 适用场景：动态维护集合关系、等价关系判断、连通性问题等。

6.2 拓展方向

本文讲了 "普通并查集"，而并查集还有两个重要的拓展方向：

• 扩展域并查集：处理元素之间的多种关系（比如朋友 / 敌人）；
• 带权并查集：为节点增加权值，维护节点间的距离、关系等信息。

这两个拓展方向我会在后续文章中详细讲解，大家感兴趣的话可以先自行了解～

6.3 学习建议

1. 先吃透基础实现和路径压缩，这是并查集的核心；
2. 多做模板题和应用题，熟悉并查集的使用场景；
3. 尝试自己实现 "按秩合并"，对比优化前后的效率；
4. 思考并查集在实际开发中的应用（比如社交网络的好友关系、地图的连通区域等）。

---

总结

并查集是算法中非常基础且实用的数据结构，掌握它不仅能应对算法竞赛，也能在日常开发中解决实际问题。希望这篇文章能帮你彻底理解并查集，下次遇到集合相关的问题，能第一时间想到这个 "神器"！