1. 基本概念
1.1 分类学习的基本思想
分类学习的目标是在样本空间中找到一个划分超平面,将不同类别的样本分开。
问题:可能存在多个划分超平面都能正确分类,应该选择哪一个?
直观想法 :选择位于两类训练样本"正中间"的划分超平面,因为该超平面对训练样本局部扰动的"容忍"性最好,具有最强的泛化能力。
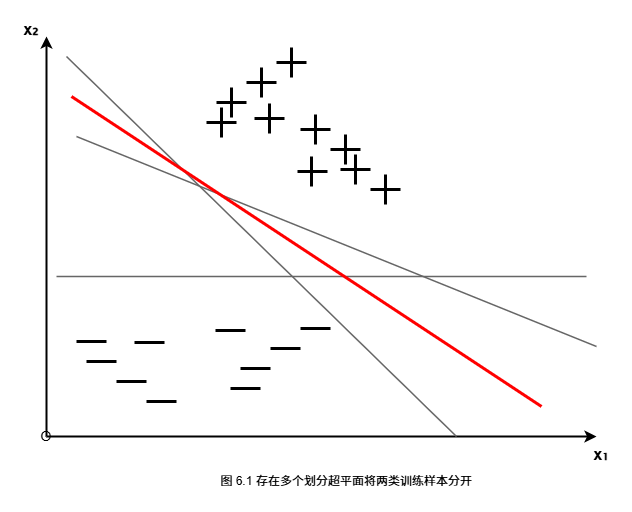
1.2 超平面的定义
在样本空间中,划分超平面可通过如下线性方程来描述:
wTx+b=0w^T x + b = 0wTx+b=0
其中:
- www 为法向量,决定了超平面的方向
- bbb 为位移项,决定了超平面与原点之间的距离
样本空间中任意点 xxx 到超平面 (w,b)(w, b)(w,b) 的距离为:
r=∣wTx+b∣∣∣w∣∣r = \frac{|w^T x + b|}{||w||}r=∣∣w∣∣∣wTx+b∣
1.3 支持向量与间隔
支持向量:距离超平面最近的训练样本点,它们决定了划分超平面的位置和方向。即使删除其他所有样本点,只保留支持向量,划分超平面也不会改变。
间隔:两个异类支持向量到超平面的距离之和,记为:
γ=2∣∣w∣∣\gamma = \frac{2}{||w||}γ=∣∣w∣∣2
间隔越大,分类的置信度越高,对训练样本的局部扰动和噪声的容忍性越强。
2. 最大间隔超平面
2.1 分类约束条件
假设超平面 (w,b)(w, b)(w,b) 能将训练样本正确分类,对于 (xi,yi)∈D(x_i, y_i) \in D(xi,yi)∈D:
- 若 yi=+1y_i = +1yi=+1,则有 wTxi+b≥+1w^T x_i + b \ge +1wTxi+b≥+1
- 若 yi=−1y_i = -1yi=−1,则有 wTxi+b≤−1w^T x_i + b \le -1wTxi+b≤−1
统一表示为:
yi(wTxi+b)≥1,i=1,2,...,my_i(w^T x_i + b) \ge 1, \quad i = 1, 2, \ldots, myi(wTxi+b)≥1,i=1,2,...,m
等号成立时,样本点位于间隔边界上,这些点就是支持向量。
2.2 SVM的基本型
为了找到具有最大间隔 的划分超平面,需要最大化间隔 γ=2∣∣w∣∣\gamma = \frac{2}{||w||}γ=∣∣w∣∣2,这等价于最小化 ∣∣w∣∣2||w||^2∣∣w∣∣2。
支持向量机的基本型:
minw,b12∣∣w∣∣2\min_{w,b} \frac{1}{2}||w||^2w,bmin21∣∣w∣∣2
s.t.yi(wTxi+b)≥1,i=1,2,...,m.\text{s.t.} \quad y_i(w^T x_i + b) \ge 1, \quad i = 1, 2, \ldots, m.s.t.yi(wTxi+b)≥1,i=1,2,...,m.
这是一个凸二次规划问题,存在全局最优解。
优化目标的意义:
- 最小化法向量的平方范数,等价于最大化间隔
- 约束条件确保所有训练样本都被正确分类
- 支持向量满足等号约束,位于间隔边界上
3. 总结
核心概念:
- 划分超平面:用于分离不同类别样本的决策边界
- 支持向量:距离超平面最近的样本点,决定超平面的位置
- 间隔 :两个异类支持向量之间的距离,γ=2∣∣w∣∣\gamma = \frac{2}{||w||}γ=∣∣w∣∣2
- 最大间隔原则:选择间隔最大的划分超平面,以获得最好的泛化性能
SVM的基本型:
minw,b12∣∣w∣∣2\min_{w,b} \frac{1}{2}||w||^2w,bmin21∣∣w∣∣2
s.t.yi(wTxi+b)≥1,i=1,2,...,m.\text{s.t.} \quad y_i(w^T x_i + b) \ge 1, \quad i = 1, 2, \ldots, m.s.t.yi(wTxi+b)≥1,i=1,2,...,m.
优势:
- 最大间隔原则提供了良好的泛化能力
- 支持向量决定了模型,模型具有稀疏性
- 优化问题是凸优化问题,有全局最优解
- 理论基础扎实,有严格的统计学习理论支撑