先来看一个具体的例子,为了简化起见,我们取 n = 2:X_1 = 一枚均匀硬币的结果(正面或反面),X_2 = 另一枚均匀硬币的结果(正面或反面)。
我们有联合概率表 P(x_1, x_2):x_1 x_2 P(x_1, x_2),正面 正面 0.25,正面 反面 0.25,反面 正面 0.25,反面 反面 0.25。
我们想要:
首先,注意到 P(x_1) 与 x_2 无关:P(正面) = 0.5, P(反面) = 0.5。所以 log P(x_1)是:
求和式如下
\begin{align*}
&-\sum_{x_1, x_2} P(x_1, x_2) \log P(x_1) \\
&= -[P(H,H) \log P(H) + P(H,T) \log P(H) + P(T,H) \log P(T) + P(T,T) \log P(T)] \\
&= -[0.25 \log 0.5 + 0.25 \log 0.5 + 0.25 \log 0.5 + 0.25 \log 0.5]
\end{align*}
分组x_1。当 x_1 = H 时,我们有两项: 。当 x_1 = T 时,我们有两项:
提取公因式 \log P(x_1),得到
对 x_2 求和,P(H,H) + P(H,T) 的值是多少?P(H,H) + P(H,T) = 0.25 + 0.25 = 0.5
但这恰恰是 P(H) 。因为:
类似地:
最后,化简
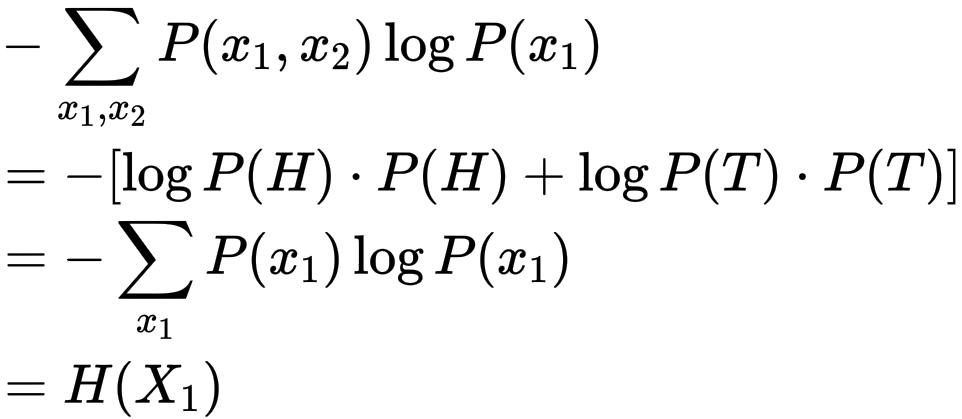
\begin{align*}
&-\sum_{x_1, x_2} P(x_1, x_2) \log P(x_1) \\
&= -[\log P(H) \cdot P(H) + \log P(T) \cdot P(T)] \\
&= -\sum_{x_1} P(x_1) \log P(x_1) \\
&= H(X_1)
\end{align*}
一般原理如下。对于任何第 k 项 ,该项仅取决于 x_1, ..., x_k。当我们对 x_{k+1}, ..., x_n 求和时:
,我们正在"积分掉"或"边缘化掉"不需要的变量。
结果恰好等于条件熵的定义:
想象一下,你有一个由更小的立方体(联合分布)组成的三维块。如果你只关心第一个坐标 x_1,你可以沿着其他维度压缩这个块,将所有具有相同 x_1 的立方体相加。你得到的是它在 x_1 轴上的投影,这就是 P(x_1)。对数 log P(x_1) 就像一个权重,它只取决于你位于 x_1 的哪个"切片"中。因此,当你对整个块求和时,你可以先在每个切片内求和,然后再应用权重。
为什么这个公式如此简洁?因为概率分布在其定义域内求和为 1。更准确地说:对于固定的 x_1,联合分布对 x_2, ... , x_n 的求和恰好等于 P(x_1)。这就像通过"积分掉"其他维度,将多维空间压缩到一维空间一样。
(csdn的公式真难用( ;´Д`))