昨天我们讲了数组与链表,今天讲一下可以由数组与链表组成的栈与队列。
第一部分:地基 ------ 内存条里的"积木"
在讨论任何数据结构之前,我们必须先理解数据(Data) 住在哪里。
1. 计算机的"草稿纸":RAM(随机存取存储器)
想象一下,你的计算机内存(RAM)就是一条无限长的、被划分成无数小格子的纸带。
-
物理现实:内存并非二维的表格,在逻辑上,它是一维的线性空间。
-
单元(Cell):每一个小格子只能存放一个字节(1 Byte = 8 bits)的数据。
-
地址(Address) :为了找到这些格子,计算机给每一个格子编了个号,从
0开始,一直到内存的尽头。这个编号就是内存地址。
关键概念:为什么叫"随机"存取?
这对理解算法复杂度 O(1) 至关重要。这意味着,CPU 访问地址为 0x0001 的格子,和访问地址为 0xFFFF 的格子,所花费的物理时间是完全一样的。计算机不需要像卷磁带一样从头卷到尾,它可以直接"瞬移"到那个地址。
2. 数据的"居住方式"
栈和队列本质上是管理数据进出的规则,但数据本身必须先存下来。在底层,数据存储只有两种最基本的形态,它们是栈和队列实现的物理基础:
A. 连续存储(Contiguous Memory)------ 数组的真身
这是计算机最喜欢的存储方式。如果你想存 3 个整数(int,假设占 4 字节),计算机就在内存里圈出一块连续的地盘。
内存视图可视化: 假设内存地址从 100 开始:
| 地址 (Address) | 数据 (Data) | 说明 |
|---|---|---|
| 100 | [Int 1 的第1字节] | \ |
| 101 | [Int 1 的第2字节] | -> 整数 1 |
| 102 | [Int 1 的第3字节] | |
| 103 | [Int 1 的第4字节] | / |
| 104 | [Int 2 的第1字节] | \ |
| 105 | ... | -> 整数 2 |
| ... | ... |
特点:紧凑、整齐。
在栈/队列中的应用 :这是实顺序栈(Array Stack)和循环队列(Circular Queue)的基础。
B. 离散存储(Non-contiguous Memory)------ 链表的真身
如果内存没有一大块连续的空间,或者你需要动态增加数据,数据就会散落在内存的各个角落。
为了把它们串起来,我们需要指针(Pointer)。
- 指针是什么? 指针本质上也是一个数据,但它存的不是"数值",而是另一个格子的地址。
内存视图可视化:
-
地址 200 存了数据 "A",同时存了一个小纸条写着:下一个在 "地址 999"。
-
地址 999 存了数据 "B",同时存了一个小纸条写着:下一个在 "地址 50"。
-
特点:灵活,但需要额外的空间存"地址"。
-
在栈/队列中的应用 :这是实现链式栈(Linked Stack)和链式队列(Linked Queue)的基础。
3. 指针:操作栈与队列的"机械臂"
在底层原理中,指针是灵魂。无论是栈的 Top(栈顶)还是队列的 Front/Rear(队头/队尾),它们在物理上通常就是一个指针(或者是一个表示偏移量的整数索引)。
想象一个机械臂(指针),它悬停在上述的"纸带"上方:
-
移动 :指针
+1,并不是数学上的加一,而是机械臂向后移动一个数据单位(比如向后移 4 个字节)。 -
解引用:机械臂抓起下面格子里的内容。
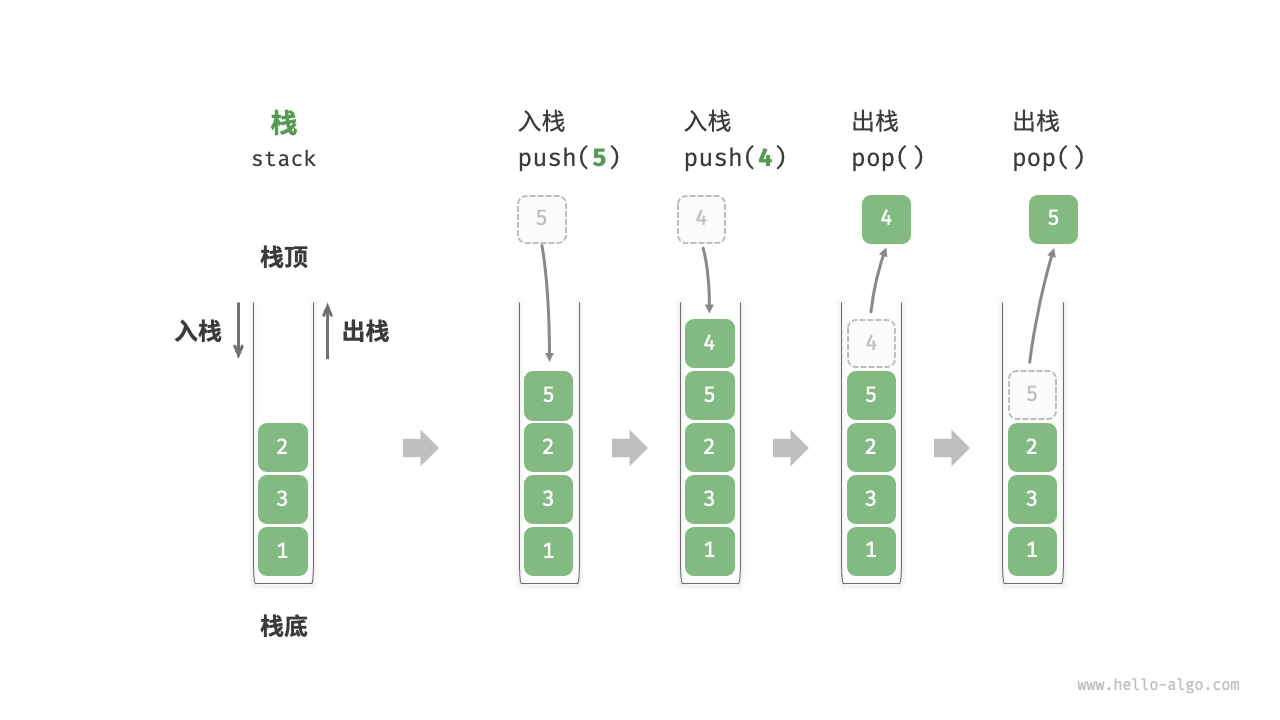
为什么这很重要? 当我们说"入栈(Push)"时,底层的物理动作其实是:
-
把数据写入当前指针指向的内存格子。
-
把指针向后移动一位(或者向前,取决于架构)。
当我们说"出栈(Pop)"时:
-
读取当前指针位置的数据。
-
把指针往回退一位。
-
注意 :原来的数据通常还在内存里,只是如果不覆盖它,我们认为它已经是"垃圾"数据了。这就是为什么在这个层面,数据删除往往很快,因为只是移动了指针而已。
这里有一个颠覆性的认知:在 CPU 眼里,栈(Stack)不仅仅是一个数据结构,它是程序能够运行的生理本能。 相比之下,队列(Queue)更多时候是软件层面人为设计的"排队规则"。
因此,这一部分我们主要聚焦于硬件栈(Hardware Stack)。
第二部分:核心 ------ CPU 视角下的"栈"与指令集
绝大多数现代 CPU(x86, ARM 等)的设计中,栈是"原生支持"的。这意味着 CPU 芯片里直接刻录了操作栈的电路和指令。
1. 领地划分:栈内存段(Stack Segment)
当你的程序(比如一个 Python 脚本)刚被操作系统加载到内存时,操作系统会大手一挥,直接在内存里划出一块固定的、连续的区域,说:"这块地盘归栈专用。"
-
栈底(Bottom):这块区域的起始位置(通常是高地址)。
-
栈顶(Top):这块区域当前数据存放到的边缘位置(通常向低地址延伸)。
2. 只有 CPU 才有特权使用的指针:SP 寄存器
CPU 内部有一组非常珍贵的存储单元,叫寄存器(Register)。它们的存取速度比内存快 100 倍以上。
其中有一个最重要的寄存器,专门用来盯着栈顶。
-
在 x86 架构中,它叫 ESP (Extended Stack Pointer) 或 RSP。
-
我们简单称之为 SP (Stack Pointer,栈指针)。
SP 的唯一任务: 永远指向栈的最顶部(也就是最新放进去的那个数据)。
3. 反直觉的物理运动:倒着长的塔
在现实生活中,我们要堆积木,是从下往上堆。 但在大多数计算机内存架构中,栈是从高地址向低地址生长的。
可视化演示: 假设栈底地址是 1000。SP 初始指向 1000。
动作 A:入栈(PUSH)一个整数 5 CPU 内部其实做了两件事:
-
移动指针 :SP 减去 4(因为一个整数占4字节)。现在 SP 指向
996。 -
写入数据 :在内存地址
996处写入5。
| 地址 | 数据 | 指针位置 |
|---|---|---|
| ... | ... | |
| 1000 | [空/旧数据] | <--- 栈底 |
| ... | ... | |
| 996 | 5 | <--- SP (栈顶) |
动作 B:再入栈(PUSH)一个整数 8
-
移动指针 :SP 再减 4。现在 SP 指向
992。 -
写入数据 :在内存地址
992处写入8。
| 地址 | 数据 | 指针位置 |
|---|---|---|
| 1000 | ... | <--- 栈底 |
| 996 | 5 | |
| 992 | 8 | <--- SP (栈顶) |
动作 C:出栈(POP) CPU 只需要做相反的事:
-
读取数据 :把 SP (
992) 指向的数据8拿出来放到 CPU 寄存器里计算。 -
回退指针 :SP 加上 4。现在 SP 回到了
996。注意:地址992里的8还在那里,但因为 SP 已经移走了,那个位置被视为"无效区域",下次入栈时会直接覆盖它。
4. 为什么 CPU 需要栈?(这是关键)
你可能会问:"CPU 算数就由着它算呗,为什么要搞个'先进后出'的栈?"
答案是为了函数调用(Function Call)。这是计算机科学中最美妙的设计之一。
想象这个场景:
-
你正在执行主函数
main()。 -
main()调用了func_A()。 -
func_A()又调用了func_B()。
问题来了: 当 func_B() 执行完那一瞬间,CPU 怎么知道该回到哪一行代码继续执行? 它必须回到 func_A() 调用它的地方,对吧?
这完全符合后进先出(LIFO) 的逻辑:
-
最后被调用的函数(
func_B),最先执行完。 -
最先开始的函数(
main),最后才结束。
函数调用的幕后过程(栈帧): 每当你调用一个函数,CPU 就会在栈里"压"入一块数据,这块数据叫栈帧(Stack Frame)。里面包含:
-
返回地址:做完这个函数后,我要跳回代码的第几行。
-
局部变量 :这个函数里定义的
x,y,z都在这。
过程模拟:
-
调用
func_A-> 压入func_A的栈帧。 -
func_A调用func_B-> 压入func_B的栈帧(现在它在栈顶)。 -
func_B执行完毕 -> 弹出func_B的栈帧(销毁局部变量),CPU 拿到返回地址,跳回func_A。 -
func_A继续执行...
5. 著名的 Stack Overflow(栈溢出)
现在你理解这个术语的物理含义了。 栈内存段的大小是有限的(比如操作系统限制为 8MB)。
如果你写了一个死循环递归:
python
def endless_recursion():
return endless_recursion()6.栈的实现
基于链表的实现
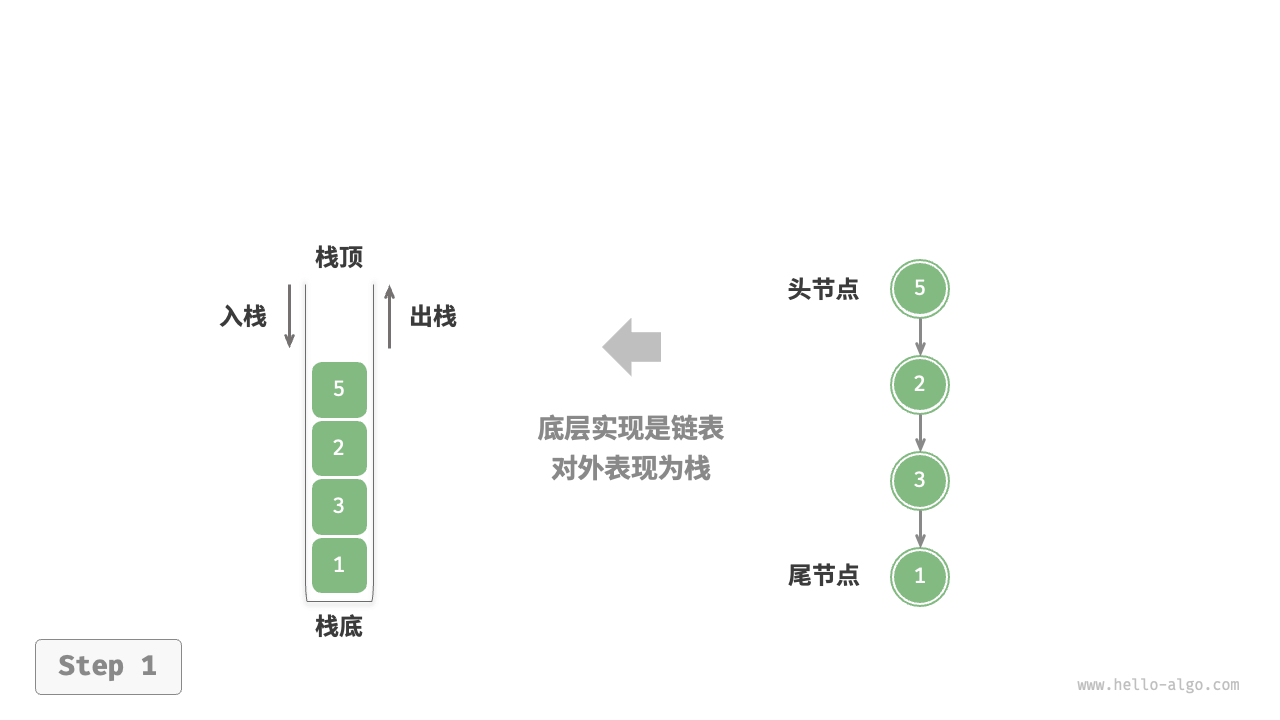
使用链表实现栈时,我们可以将链表的头节点视为栈顶,尾节点视为栈底。
对于入栈操作,我们只需将元素插入链表头部,这种节点插入方法被称为"头插法"。而对于出栈操作,只需将头节点从链表中删除即可。
python
# === 节点类:模拟内存中的一个小格子 ===
class Node:
def __init__(self, value):
self.value = value # 存放数据
self.next = None # 存放下一个节点的地址(指针)
# === 栈:链表版实现 ===
class HardStack:
def __init__(self):
# 只需要一个指针,永远指向栈顶
self.top = None
def push(self, val):
new_node = Node(val) # 1. 申请一块新内存(创建节点)
# 核心逻辑:
# 把新节点的 next 指向当前的栈顶(让新来的踩在旧的头顶上)
new_node.next = self.top
# 更新 top 指针,现在新节点才是栈顶
self.top = new_node
print(f"链表入栈: {val}")
def pop(self):
if self.top is None:
return None
# 1. 拿到当前栈顶的数据
val = self.top.value
# 2. 核心逻辑:移动 top 指针
# 既然栈顶要走了,新的栈顶就是原来栈顶脚下的那个(next)
self.top = self.top.next
return val
# --- 测试 ---
# 想象一下:内存里本来散落着数据,现在被这一根线串起来了
hs = HardStack()
hs.push(10)
hs.push(20) # 20 -> 10 -> None
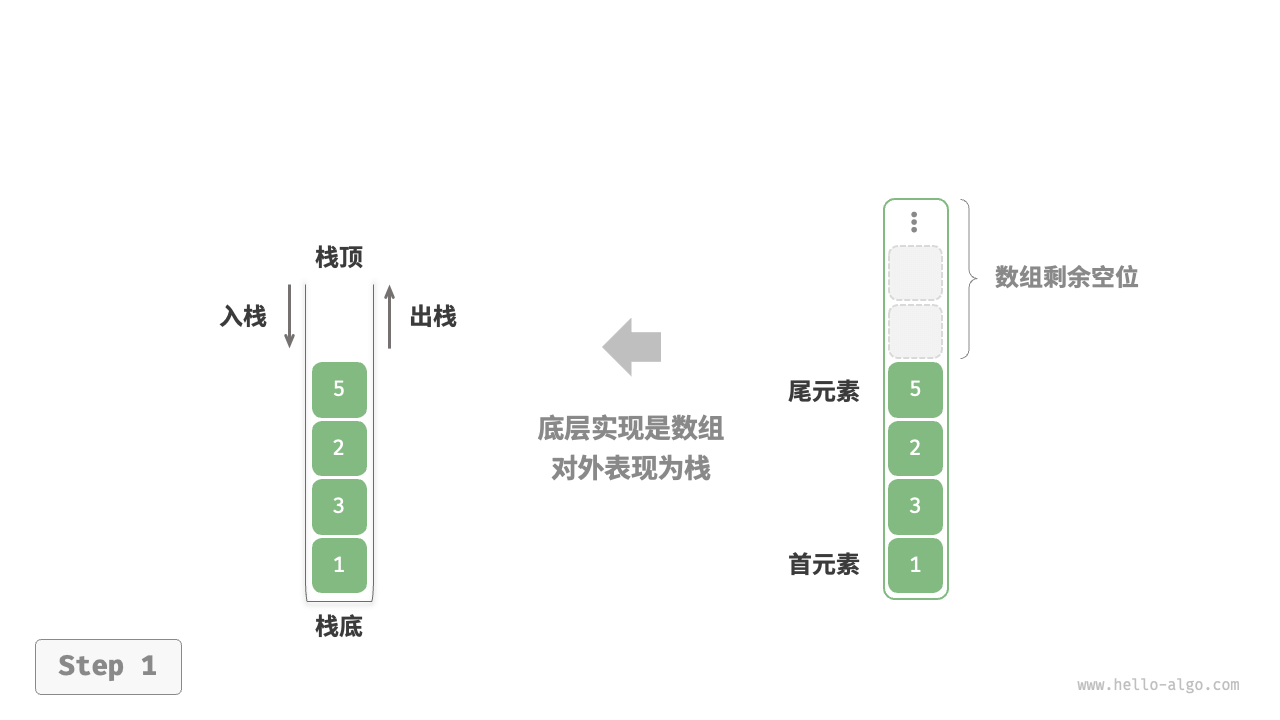
print(hs.pop()) # 20基于数组的实现:
python
class ArrayStack:
"""基于数组实现的栈"""
def __init__(self):
"""构造方法"""
self._stack: list[int] = []
def size(self) -> int:
"""获取栈的长度"""
return len(self._stack)
def is_empty(self) -> bool:
"""判断栈是否为空"""
return self.size() == 0
def push(self, item: int):
"""入栈"""
self._stack.append(item)
def pop(self) -> int:
"""出栈"""
if self.is_empty():
raise IndexError("栈为空")
return self._stack.pop()
def peek(self) -> int:
"""访问栈顶元素"""
if self.is_empty():
raise IndexError("栈为空")
return self._stack[-1]
def to_list(self) -> list[int]:
"""返回列表用于打印"""
return self._stack第二部分总结
在这一层,我们学到了:
-
栈是硬件特性:CPU 有专门的 SP 寄存器来追踪它。
-
生长方向:在物理内存中,栈通常是从高地址向低地址"倒着长"的。
-
函数调用即入栈 :我们写的每一行函数调用,底层都是一次
PUSH动作;函数返回,就是POP动作。
现在,物理和硬件原理我们都懂了。 但是,我们在写 Python 或 C++ 代码时,通常不会直接去操作 SP 寄存器。我们需要更高级的"抽象"。
同时,我们还没详细讲队列 。因为队列在 CPU 硬件层面上不如栈那么核心,它更多是在软件和算法层面发光发热。
第三部分:架构 ------ 软件实现与算法灵魂
在软件层面,我们将栈和队列称为 ADT(抽象数据类型) 。意思是:我不关心你在底层是用数组还是链表实现的,我只关心你对外提供的功能。
但作为架构师,我们必须知道底层实现的代价。这里最大的挑战在于队列。
1. 队列的物理难题:它会"爬行"
还记得栈吗?栈很老实,指针只在一个固定的底部来回晃动,数据利用率极高。
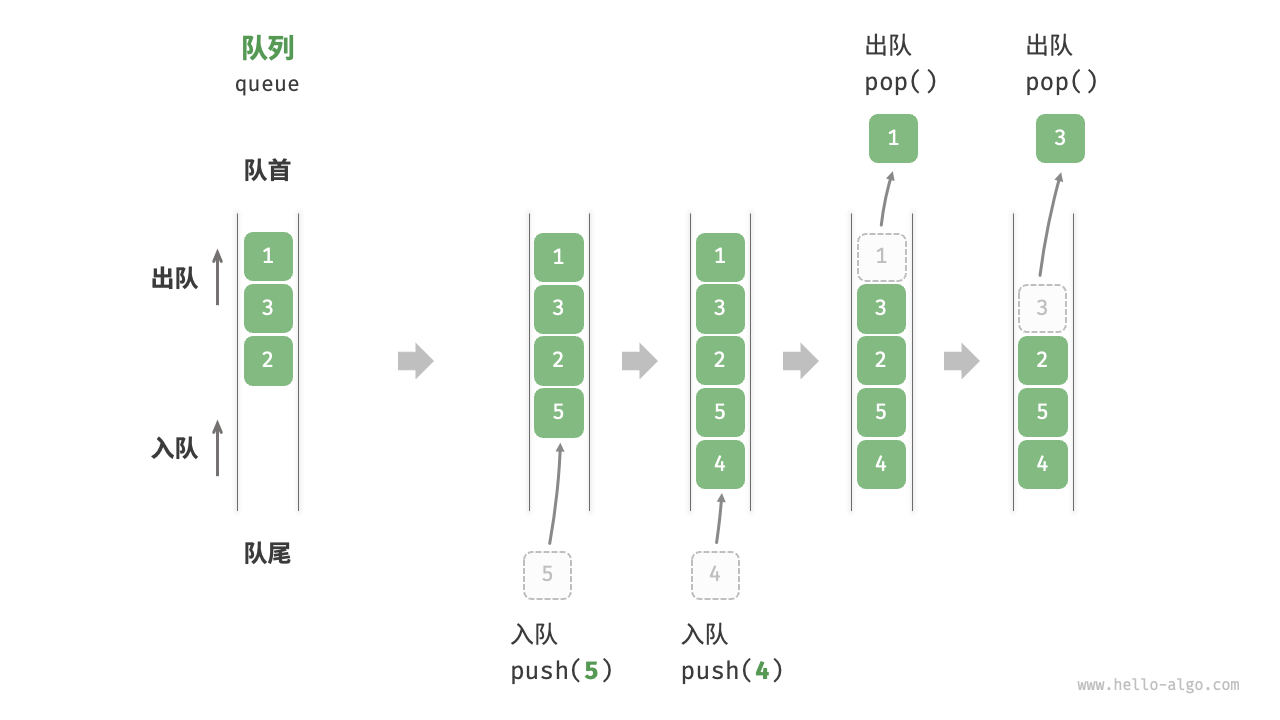
但队列是"先进先出"(FIFO)。这意味着:
-
入队(Enqueue):在尾巴加数据。
-
出队(Dequeue):在头部拿数据。
这就产生了一个物理难题------"假溢出": 想象你在内存里开辟了一个长度为 5 的数组来实现队列。
-
你入队 5 个元素,填满了数组。
-
你出队 3 个元素。此时,数组的前 3 个格子空了。
-
关键点:虽然前 3 个格子空了,但你的"队尾指针"还在数组的最后面!计算机呆呆地告诉你:"队尾满了,不能加人了。"
这就像排队买票,队伍往前走了,但窗口却不让后面的人跟进空出来的位置,导致队伍后面有一大截空地,却还在喊"满员"。
为了解决这个问题,软件工程师发明了两个经典的底层架构:
A. 搬砖法(低效)
每次出队一个人,就把后面所有的人往前挪一位。
- 代价 :这需要极大的计算量。如果你有 1 万个数据,出队 1 个,就要搬运 9999 次数据。这在算法上叫 O(n) 复杂度。绝对不可取。
B. 环形缓冲(Circular Buffer / Ring Buffer)------ 优雅的解法
这是操作系统和高性能网络包处理中最常用的技巧。
我们把直线的内存数组,在逻辑上想象成一个圆环。
-
原理 :当队尾指针走到数组的尽头(比如索引 9),下一个位置不是报错,而是通过数学运算(取模运算
%)瞬间回到数组的开头(索引 0)。 -
结果:只要圆环里还有空位,队伍就可以永远不停地转圈圈流动,完全不需要搬运数据。
-
复杂度 :入队和出队都是完美的 O(1)。
2. Python 中的陷阱与真相
基于上述原理,我们来看看 Python 中的实现,你会豁然开朗。
栈的实现
Python 的 list 本质上就是动态数组。
-
list.append():就是入栈。 -
list.pop():就是出栈(默认弹最后一个)。 -
评价:非常高效,符合 CPU 缓存原理,速度极快。
队列的实现(大坑)
很多新手喜欢用 list 做队列:
-
入队:
list.append() -
出队:
list.pop(0)------ 千万别这么做!
底层原理分析 :list 是连续内存。当你 pop(0) 删掉第 0 个元素时,Python 为了保持内存连续性,必须把后面成千上万个元素全部向前移动一位(就是我们刚才说的"搬砖法")。这会把 CPU 累死。
正确的做法 :使用 collections.deque。
-
deque的底层通常是用双向链表 (Doubly Linked List)或者分段数组实现的。 -
链表原理:删掉第一个节点,只需要断开指针,后面的人不需要动。
-
所以,在 Python 里做队列,必须 用
deque。
python
class Node:
def __init__(self, value):
self.value = value
self.next = None
class HardQueue:
def __init__(self):
self.front = None # 队头(出队用)
self.rear = None # 队尾(入队用)
def enqueue(self, val):
new_node = Node(val)
if self.rear is None:
# 如果队列是空的,头尾都是这个新节点
self.front = new_node
self.rear = new_node
else:
# 1. 让现在的队尾指向新节点(接上队伍)
self.rear.next = new_node
# 2. 更新队尾指针,指向最新的末尾
self.rear = new_node
print(f"链表入队: {val}")
def dequeue(self):
if self.front is None:
return None
# 1. 拿数据
val = self.front.value
# 2. 移动队头指针(让第二个人变成排头的)
self.front = self.front.next
# 3. 特殊情况:如果你出队后,队伍空了
if self.front is None:
self.rear = None # 队尾也要置空
return val
# --- 测试 ---
hq = HardQueue()
hq.enqueue("A")
hq.enqueue("B") # 队列形态:A -> B
print(hq.dequeue()) # 输出 A,队列剩下 B3. 算法灵魂:深度 vs 广度
最后,我们升华一下。栈和队列不仅仅是存储数据的容器,它们代表了两种截然不同的解决问题的哲学。
栈(Stack)------ 执着者
-
哲学:一条路走到黑,不撞南墙不回头。
-
对应算法 :DFS(深度优先搜索)。
-
场景:走迷宫。
-
遇到岔路口,把当前位置压入栈。
-
选一条路一直走下去。
-
如果是死胡同,就出栈(回溯),回到上一个路口,换条路走。
-
-
本质:栈保存了"我从哪里来"的历史,让我们可以时光倒流。
队列(Queue)------ 公平者
-
哲学:雨露均沾,层层推进。
-
对应算法 :BFS(广度优先搜索)。
-
场景:水波纹扩散、寻找最近的好友。
-
不像栈那样一头扎进去,而是先把周围邻居都看一遍(入队)。
-
按照先来后到的顺序,处理邻居,再看邻居的邻居。
-
-
本质:队列保证了处理顺序的公平性,也保证了我们找到的一定是"最近"的路径。