进阶数据结构应用-线段树扫描线

题目-亚特兰蒂斯

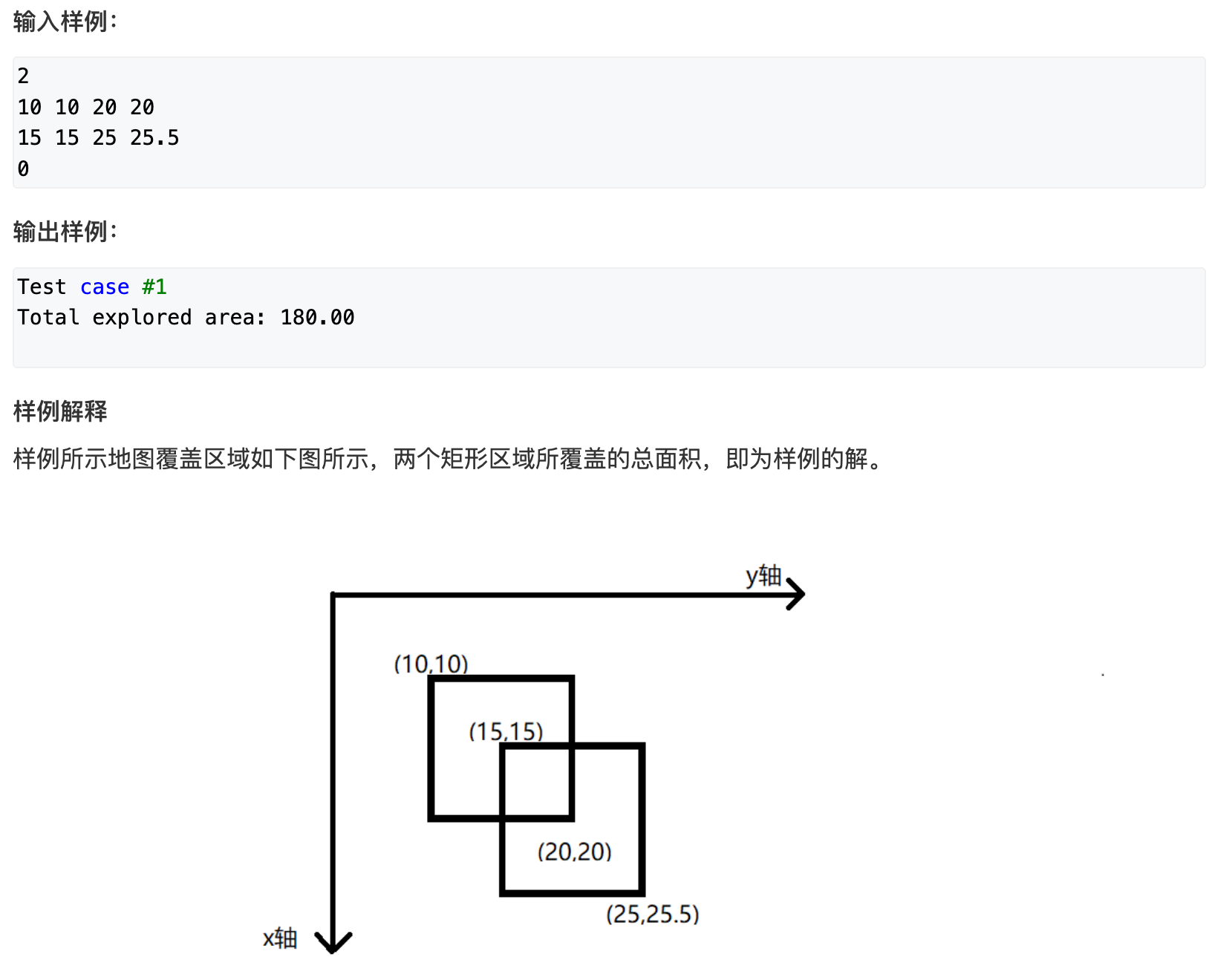
问题分析

计算面积的并集

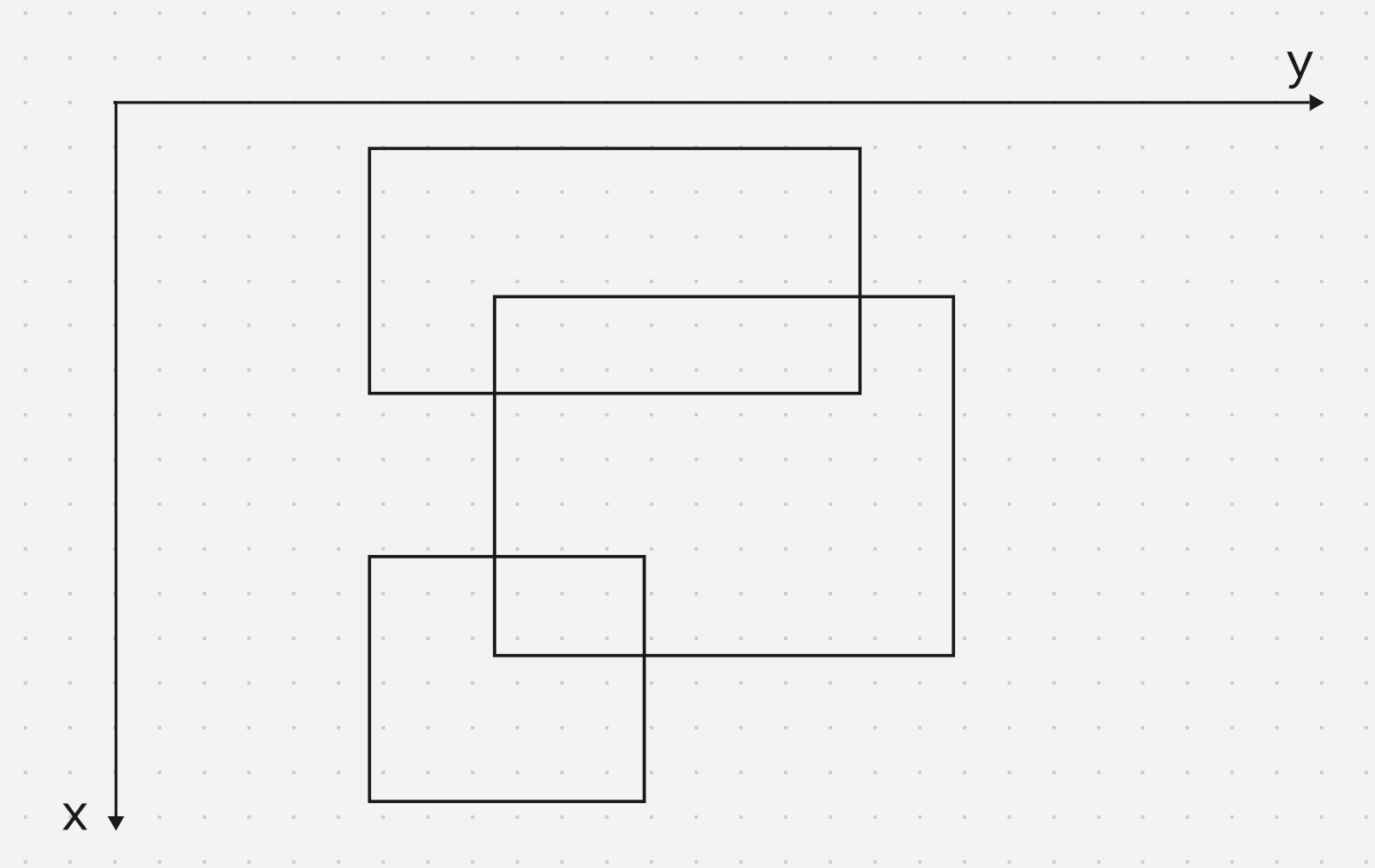
类似于扫描的思想, 只要是 y y y不连续, 将面积从左到右做细分

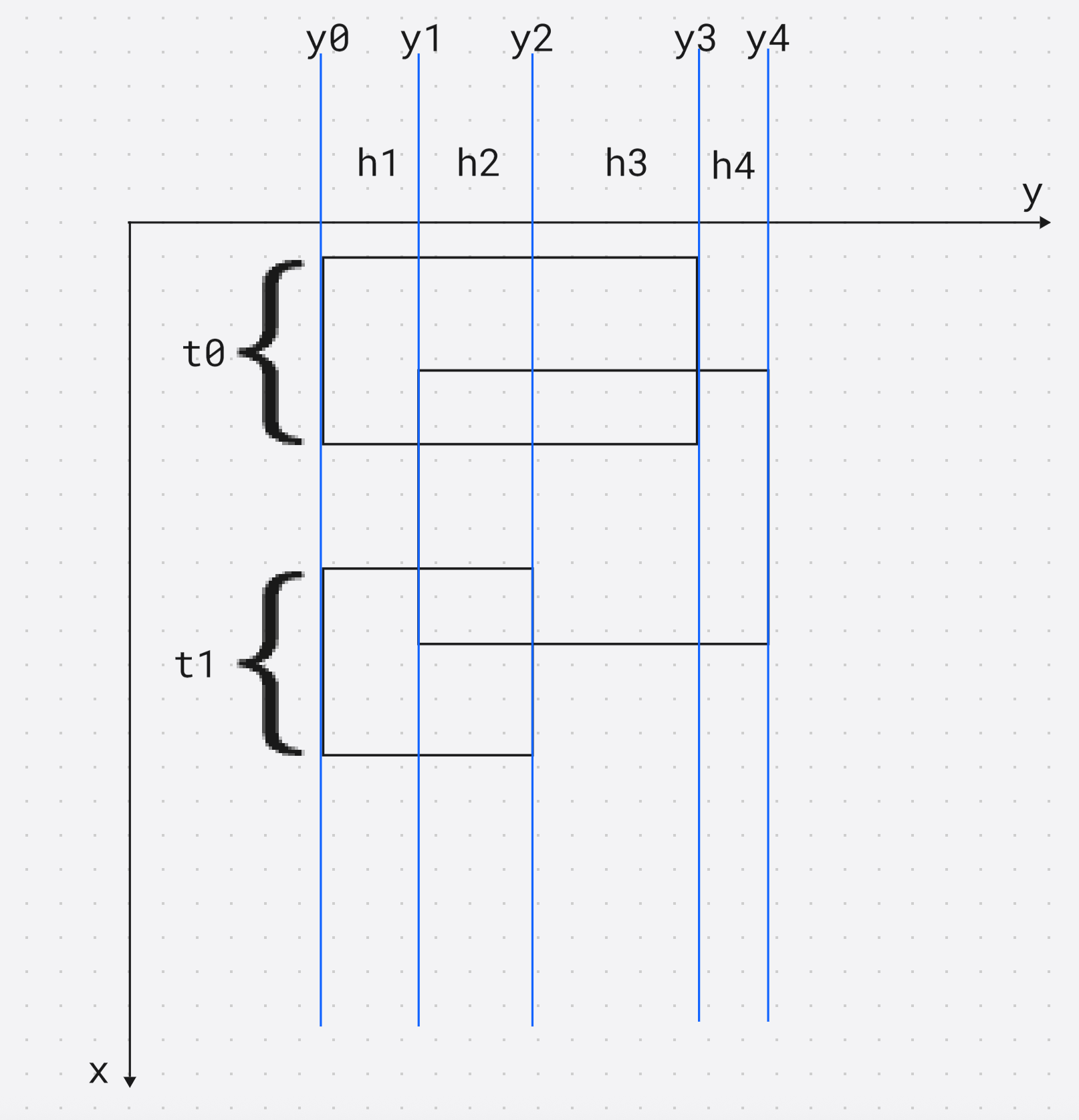
设 h 1 = t 0 + t 1 h_1= t_0 + t_1 h1=t0+t1, 同理 h 2 h_2 h2就是下一段的 x x x的差值, 那么总的覆盖面积 就是
∑ i = 1 n h i ⋅ ( y i − y i − 1 ) \sum {i = 1} ^ n h_i \cdot (y_i - y{i - 1}) i=1∑nhi⋅(yi−yi−1)

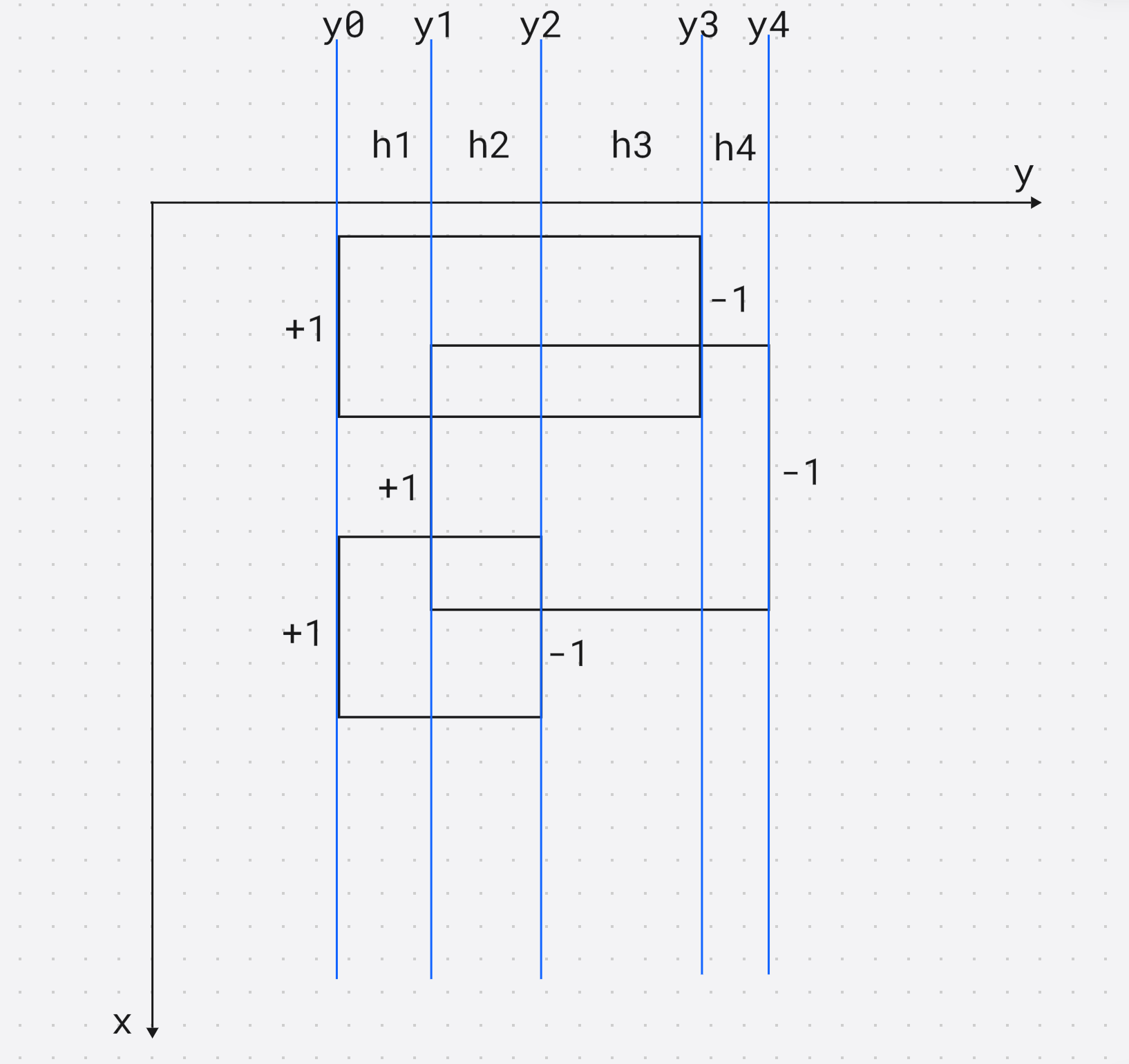
将矩形的边做成带权值的线段 , 扫描到的时候 + 1 + 1 +1, 离开的时候 − 1 - 1 −1

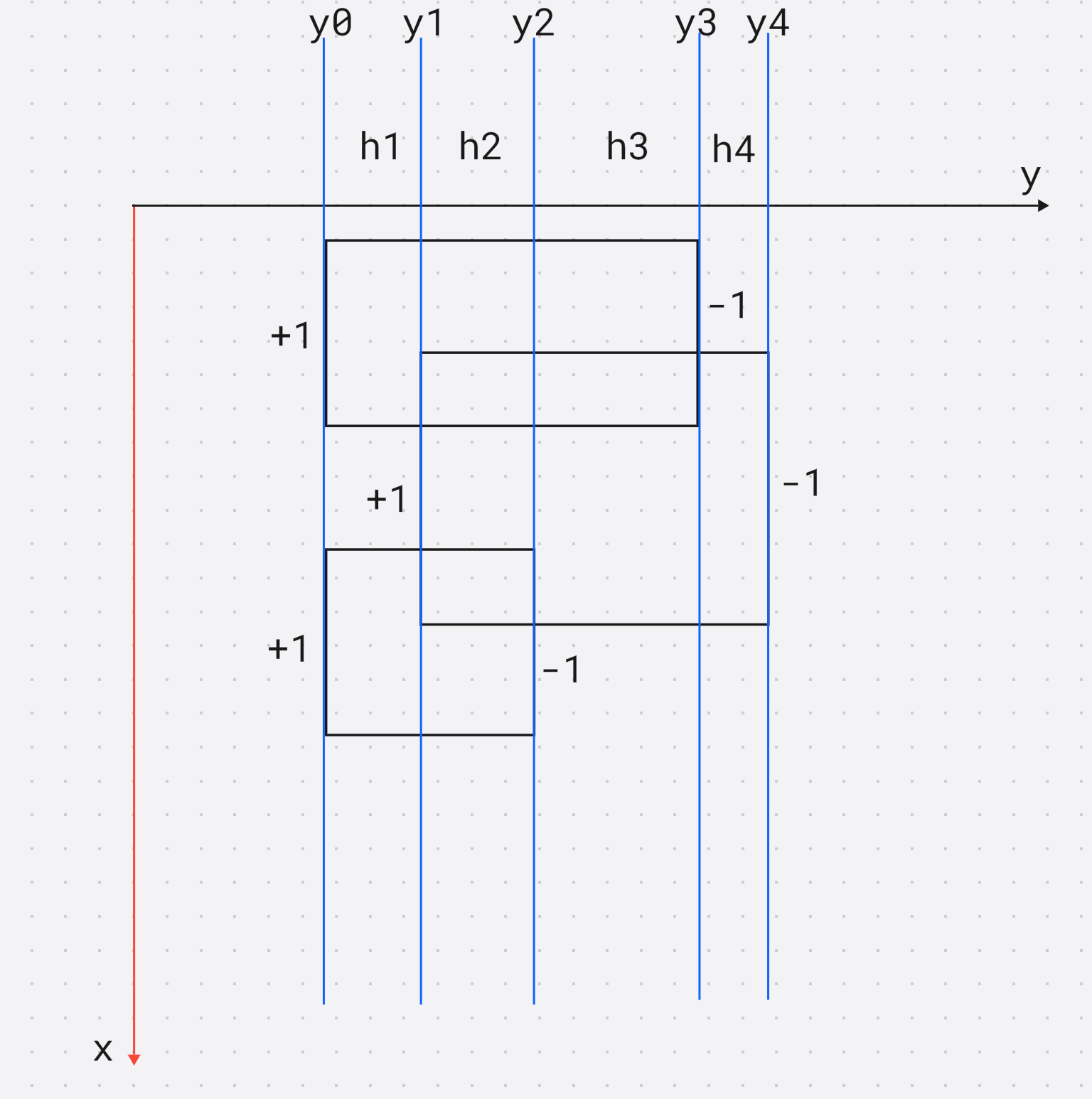
映射到 x x x上, x x x上建立线段树, 检查当前 x x x轴线段树上有多少个区间的值大于 0 0 0

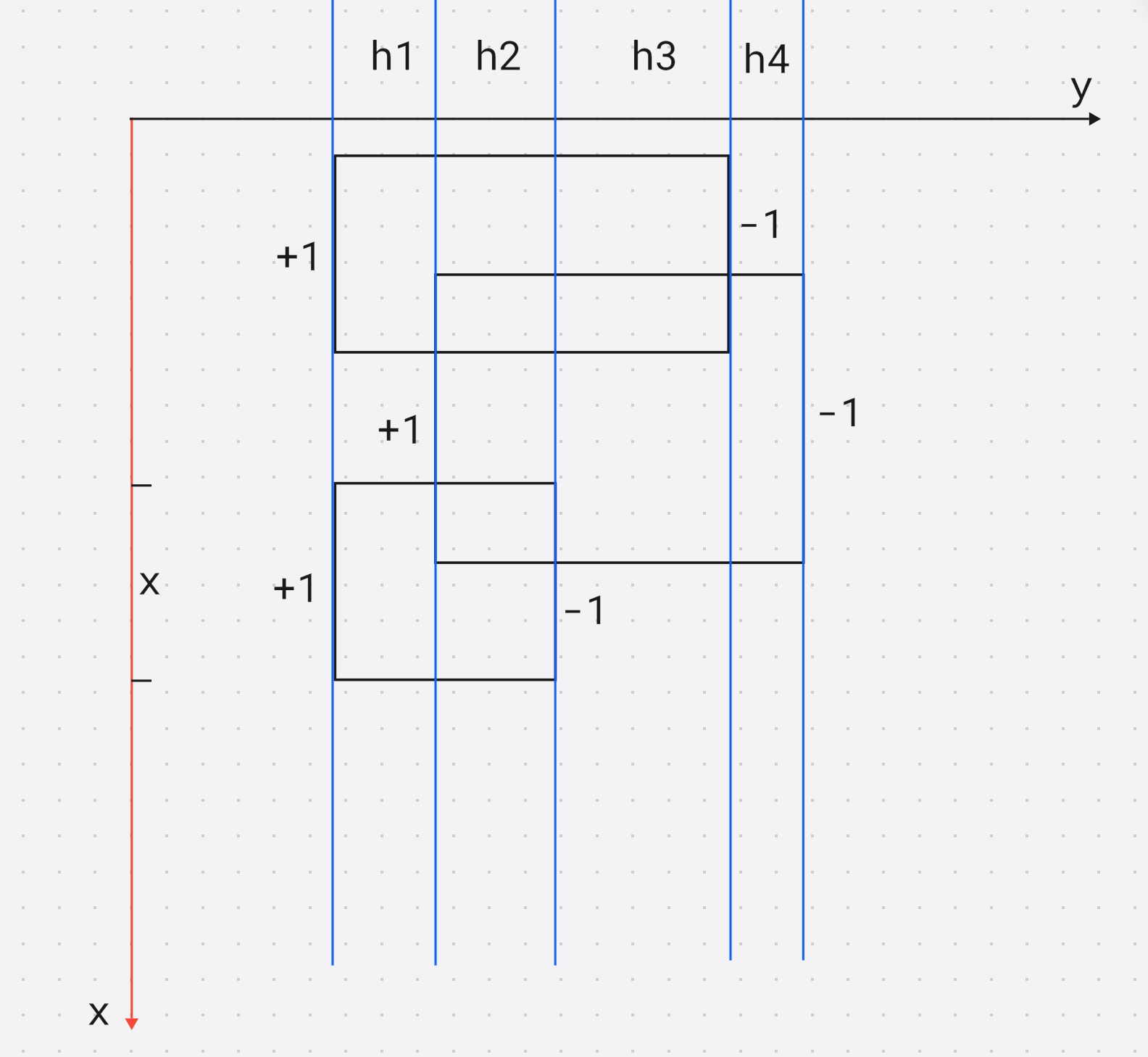
当前这一段 x > 0 x > 0 x>0等价与当前这段区间被 x x x个矩形覆盖, 需要累加到答案当中

抽象为线段树的两个操作

将区间 [ L , R ] [L, R] [L,R]加上 k k k
求整个区间中权值大于 0 0 0的区间总长度

线段树维护的节点信息

c n t cnt cnt当前区间被覆盖的次数
s u m sum sum表示不考虑祖先节点 c n t cnt cnt情况下, c n t > 0 cnt > 0 cnt>0的权值之和

扫描线有如下性质

只查询根节点 , 因此查询过程中直接返回不会递归 , 因此不会用到push down操作
修改的时候也不需要push down, 因为所有的区间操作 都是成对出现 , 并且区间先 + + +后 − - −, 对于每个矩形来说, 只会 + + +一次, − - −一次, 并且修改的区间节点 是一致的, 因此不需要push down操作

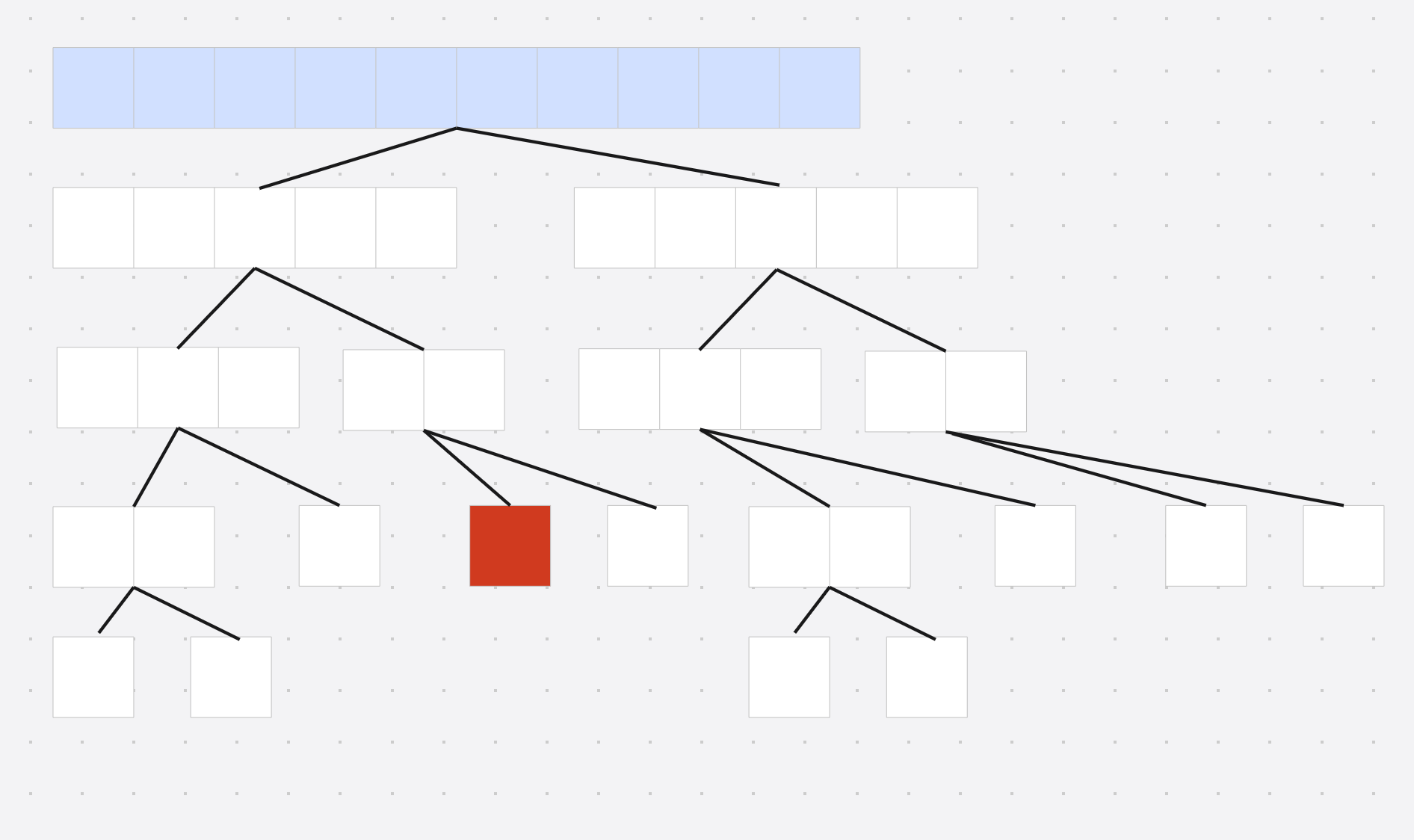
具体的来说, 假设线段树修改到了上面红色的节点(子节点), 但是每次查询只查询根节点(蓝色), 只会用到根节点的两个子节点 的信息

在修改完子节点回溯的过程中向上更新(添加减少的都是相同的子节点的值), 也就是一个节点所代表的区间被覆盖次数不需要继承父节点信息

并且不会查询到子区间分裂的情况 , 因此不需要push down操作

算法步骤

读入坐标
将矩形分为两类, 一类是 + 1 +1 +1, 一类是 − 1 -1 −1, 同时将 y y y离散化
假设离散化后有 m m m个点, 实际是 m − 1 m - 1 m−1个区间, 线段树每个节点存储的是区间而不是点 , 因此线段树的区间索引是 0 ∼ m − 2 0 \sim m - 2 0∼m−2
因此对于线段树节点假设是 [ l , r ] [l, r] [l,r], 对应实际的点的坐标是 [ l , r + 1 ] [l, r + 1] [l,r+1], 因此如果当前线段树维护的区间被覆盖(cnt != 0), 实际被覆盖的长度tr[u].sum = (nums[r + 1] - nums[l])

代码实现

cpp 复制代码

#include <bits/stdc++.h>

const int N = 1e5 + 10;
using namespace std;

int T = 1, n;
struct Seg {
    double x, y1, y2;
    int val;
    bool operator< (const Seg &s) const {
        return x < s.x;
    }
} segs[N << 1];
struct Node {
    int l, r;
    int cnt;
    double sum;
} tr[N << 3];
vector<double> nums;

int find(double x) {
    return lower_bound(nums.begin(), nums.end(), x) - nums.begin();
}

void pushup(int u) {
    if (tr[u].cnt) {
        // 因为线段树[l, r]存储的是区间下标, 对应的离散化后点的下标是[l + 1, r]
        tr[u].sum = nums[tr[u].r + 1] - nums[tr[u].l];
    }
    // 当前区间未被覆盖, 实际的被覆盖的长度等于子节点覆盖的长度
    else if (tr[u].l != tr[u].r) {
        tr[u].sum = tr[u << 1].sum + tr[u << 1 | 1].sum;
    }
    // 当前区间未被覆盖并且也不存在子节点
    else {
        tr[u].sum = 0;
    }
}

void build(int u, int l, int r) {
    tr[u] = {l, r, 0, 0};
    if (l == r) return;
    int mid = l + r >> 1;
    build(u << 1, l, mid), build(u << 1 | 1, mid + 1, r);
}

void modify(int u, int ql, int qr, int val) {
    if (tr[u].l >= ql && tr[u].r <= qr) {
        tr[u].cnt += val;
        // 当前值或者两个儿子的值计算一下
        pushup(u);
        return;
    }

    int mid = tr[u].l + tr[u].r >> 1;
    if (ql <= mid) modify(u << 1, ql, qr, val);
    if (qr > mid) modify(u << 1 | 1, ql, qr, val);

    pushup(u);
}


void solve() {
    nums.clear();

    int cnt = 0;
    for (int i = 0; i < n; ++i) {
        double x1, y1, x2, y2;
        cin >> x1 >> y1 >> x2 >> y2;
        segs[cnt++] = {x1, y1, y2, 1};
        segs[cnt++] = {x2, y1, y2, -1};
        nums.push_back(y1), nums.push_back(y2);
    }

    sort(segs, segs + cnt);
    sort(nums.begin(), nums.end());
    nums.erase(unique(nums.begin(), nums.end()), nums.end());

    int m = nums.size();
    build(1, 0, m - 2);

    double ans = 0;
    for (int i = 0; i < cnt; ++i) {
        if (i > 0) ans += tr[1].sum * (segs[i].x - segs[i - 1].x);
        Seg &s = segs[i];
        modify(1, find(s.y1), find(s.y2) - 1, s.val);
    }

    printf("Test case #%d\n", T++);
    printf("Total explored area: %.2lf\n\n", ans);
}

int main() {
    ios::sync_with_stdio(false);
    cin.tie(0);

    while (cin >> n, n) solve();

    return 0;
}

进阶数据结构应用-线段树扫描线

目录

题目-亚特兰蒂斯

问题分析

算法步骤

代码实现