一，二叉搜索树的回顾以及性能分析
1.1二叉搜索树的概念
二叉搜所树又称二叉排序树，它或者是一颗空树，或者是具有以下性质的二叉树：
若它的左子树不为空，则左子树上所有节点的值都小于根节点的值
若它的右子树不为空，则右子树上所有的节点值都大于根节点的值
它的左右子树也分别为二叉搜索树。
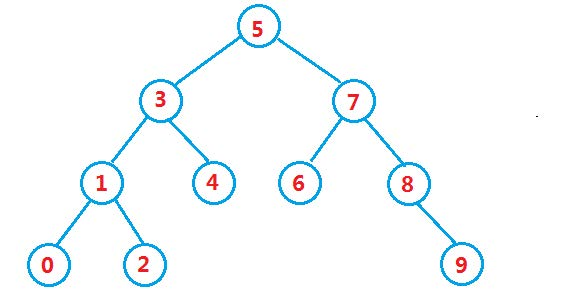
大小排序，类似于中序排序，从小到大排序为左根右。
1.2二叉搜索树的查找
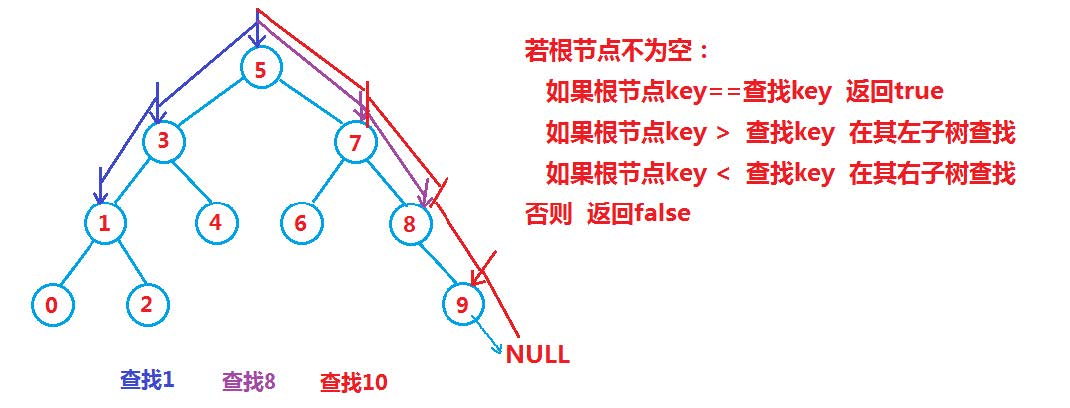
1.3二叉树查询性能分析
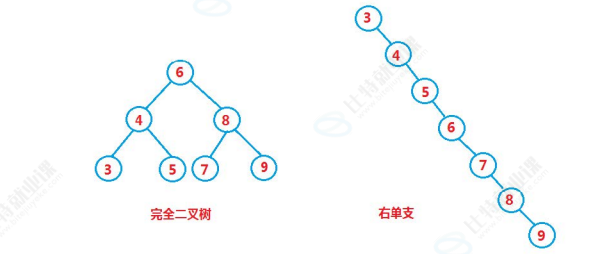
最优的情况下，二叉搜索树为完全二叉树，其平均比较次数为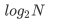
最差的情况下，二叉搜索树为单只树，其平均的比较次数为：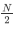
1.4普通搜索树 /单只树→ 最优 搜索二叉树
核心步骤1. 遍历普通树提取所有节点值；2. 排序得到升序序列；3. 分治法构建平衡 BST。
java
class TreeNode{
int val;
TreeNode left;
TreeNode right;
TreeNode(int val){
this.val=val
}
// 方便打印树（层序遍历）
@Override
public String toString() {
return String.valueOf(val);
}
}
java
public class BSTOptimizer {
// ========== 工具方法：收集普通树的所有节点值（用于非BST转BST） ==========
public static void collectAllNodes(TreeNode root, List<Integer> values) {
if (root == null) return;
values.add(root.val);
collectAllNodes(root.left, values);
collectAllNodes(root.right, values);
}
// ========== 工具方法：BST的中序遍历（提取有序序列） ==========
public static void inorderTraversal(TreeNode root, List<Integer> values) {
if (root == null) return;
inorderTraversal(root.left, values); // 左
values.add(root.val); // 中
inorderTraversal(root.right, values);// 右
}
// ========== 核心：有序数组转最优BST（分治法） ==========
public static TreeNode sortedArrayToBalancedBST(List<Integer> sortedVals, int start, int end) {
// 递归终止条件：区间无效
if (start > end) return null;
// 取中间元素为根（保证左右子树均衡）
int mid = start + (end - start) / 2;
TreeNode root = new TreeNode(sortedVals.get(mid));
// 递归构建左子树（左半区间）
root.left = sortedArrayToBalancedBST(sortedVals, start, mid - 1);
// 递归构建右子树（右半区间）
root.right = sortedArrayToBalancedBST(sortedVals, mid + 1, end);
return root;
// ========== 统一转换入口：普通树/单支BST → 最优BST ==========
/**
* @param root 原树根节点
* @param isLegalBST 是否为合法BST（单支BST传true，普通树传false）
* @return 最优BST的根节点
*/
public static TreeNode convertToOptimalBST(TreeNode root, boolean isLegalBST) {
List<Integer> values = new ArrayList<>();
if (isLegalBST) {
// 合法BST：中序遍历提取有序序列
inorderTraversal(root, values);
} else {
// 普通树：收集所有值并排序
collectAllNodes(root, values);
Collections.sort(values);
}
// 分治法构建最优BST
return sortedArrayToBalancedBST(values, 0, values.size() - 1);
}
}
java
public class TestBSTOptimizer {
public static void main(String[] args) {
// ========== 测试1：单支BST（只有右孩子）转最优BST ==========
System.out.println("===== 单支BST转最优BST =====");
// 构建单支BST：1 → 2 → 3 → 4 → 5（只有右孩子，高度4）
TreeNode singleBranchRoot = new TreeNode(1);
singleBranchRoot.right = new TreeNode(2);
singleBranchRoot.right.right = new TreeNode(3);
singleBranchRoot.right.right.right = new TreeNode(4);
singleBranchRoot.right.right.right.right = new TreeNode(5);
System.out.println("原单支BST结构（层序）：");
BSTOptimizer.printTree(singleBranchRoot);
// 转换为最优BST（isLegalBST=true，因为单支BST是合法BST）
TreeNode optimalBST1 = BSTOptimizer.convertToOptimalBST(singleBranchRoot, true);
System.out.println("转换后最优BST结构（层序）：");
BSTOptimizer.printTree(optimalBST1);
// ========== 测试2：普通树（非BST）转最优BST ==========
System.out.println("\n===== 普通树转最优BST =====");
// 构建普通树（无BST属性：根3，左5，右1，左左2，右右4）
TreeNode normalRoot = new TreeNode(3);
normalRoot.left = new TreeNode(5);
normalRoot.right = new TreeNode(1);
normalRoot.left.left = new TreeNode(2);
normalRoot.right.right = new TreeNode(4);
System.out.println("原普通树结构（层序）：");
BSTOptimizer.printTree(normalRoot);
// 转换为最优BST（isLegalBST=false，普通树非BST）
TreeNode optimalBST2 = BSTOptimizer.convertToOptimalBST(normalRoot, false);
System.out.println("转换后最优BST结构（层序）：");
BSTOptimizer.printTree(optimalBST2);
}
}核心逻辑
- 分治法的核心：取有序数组中间元素为根，保证左右子树节点数尽可能相等，树高度最小（最优）；
- 时间复杂度 ：
- 单支 BST 转换：O (n)（中序遍历 + 分治构建）；
- 普通树转换：O (nlogn)（收集 + 排序 + 分治构建）；
- 空间复杂度：O (n)（存储有序序列 + 递归栈）；
- 扩展性：若需严格的平衡 BST（如 AVL 树 / 红黑树），可在分治构建后增加平衡校验（旋转操作），但上述方法已满足「最优情况」（高度最小）。
拓展整合排序方法代码
java
import java.util.ArrayList;
import java.util.List;
import java.util.Arrays; // 补充导入，用于打印数组
// 简化的TreeNode类（你已经会了，这里再写一遍方便完整运行）
class TreeNode {
int val;
TreeNode left;
TreeNode right;
TreeNode(int val) { this.val = val; }
}
public class BalanceBSTConverter {
// 第一步：提取二叉树所有节点值（支持任意二叉树，包括单支BST）
public static List<Integer> extractValues(TreeNode root) {
List<Integer> values = new ArrayList<>();
// 用后序遍历收集所有节点值，避免遗漏（也可以用层序、中序，结果一样）
traverse(root, values);
return values;
}
// 辅助遍历方法（后序遍历）
private static void traverse(TreeNode node, List<Integer> values) {
if (node == null) return;
traverse(node.left, values); // 左
traverse(node.right, values); // 右
values.add(node.val); // 根
}
// 补充：单支BST专用------中序遍历（直接获取有序数组，省排序步骤）
private static void inorderTraversal(TreeNode root, List<Integer> values) {
if (root == null) return;
inorderTraversal(root.left, values); // 左（单支BST此处为空）
values.add(root.val); // 中（核心：BST中序=升序）
inorderTraversal(root.right, values); // 右（单支BST的节点都在这里）
}
// 第二步：多种排序方法（可直接切换）
// 1. 插入排序（适合小数据量，简单易理解）
public static void insertionSort(int[] arr) {
int n = arr.length;
for (int i = 1; i < n; i++) {
int key = arr[i];
int j = i - 1;
// 把比key大的元素往后移
while (j >= 0 && arr[j] > key) {
arr[j + 1] = arr[j];
j--;
}
arr[j + 1] = key; // 插入key到正确位置
}
}
// 2. 快速排序（适合大数据量，效率高）
public static void quickSort(int[] arr) {
quickSortHelper(arr, 0, arr.length - 1);
}
private static void quickSortHelper(int[] arr, int low, int high) {
if (low < high) {
int pivotIndex = partition(arr, low, high); // 找基准点位置
quickSortHelper(arr, low, pivotIndex - 1); // 排序左半部分
quickSortHelper(arr, pivotIndex + 1, high); // 排序右半部分
}
}
// 快速排序分区方法（以最后一个元素为基准）
private static int partition(int[] arr, int low, int high) {
int pivot = arr[high];
int i = low - 1; // 记录小于基准的元素位置
for (int j = low; j < high; j++) {
if (arr[j] <= pivot) {
i++;
// 交换arr[i]和arr[j]
int temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
}
}
// 把基准点放到正确位置（i+1）
int temp = arr[i + 1];
arr[i + 1] = arr[high];
arr[high] = temp;
return i + 1;
}
// 3. 希尔排序（插入排序的优化，适合中等数据量）
public static void shellSort(int[] arr) {
int n = arr.length;
// 初始步长设为n/2，逐步缩小步长到1
for (int gap = n / 2; gap > 0; gap /= 2) {
// 按步长gap进行插入排序
for (int i = gap; i < n; i++) {
int key = arr[i];
int j = i;
// 同组内比key大的元素往后移
while (j >= gap && arr[j - gap] > key) {
arr[j] = arr[j - gap];
j -= gap;
}
arr[j] = key; // 插入key
}
}
}
// 第三步：有序数组转平衡BST（分治法核心）
public static TreeNode sortedArrayToBalancedBST(int[] sortedArr) {
return buildTree(sortedArr, 0, sortedArr.length - 1);
}
// 辅助构建平衡BST的递归方法
private static TreeNode buildTree(int[] arr, int left, int right) {
if (left > right) return null; // 递归终止条件：区间为空
// 取中间元素为根节点（避免溢出，等价于(left+right)/2）
int mid = left + (right - left) / 2;
TreeNode root = new TreeNode(arr[mid]);
// 递归构建左子树（左半区间[left, mid-1]）
root.left = buildTree(arr, left, mid - 1);
// 递归构建右子树（右半区间[mid+1, right]）
root.right = buildTree(arr, mid + 1, right);
return root; // 返回当前子树的根
}
// 补充：辅助打印BST（层序遍历，直观看到平衡结构）
public static void printBST(TreeNode root) {
if (root == null) {
System.out.println("空树");
return;
}
List<TreeNode> queue = new ArrayList<>();
queue.add(root);
while (!queue.isEmpty()) {
int size = queue.size();
for (int i = 0; i < size; i++) {
TreeNode node = queue.remove(0);
System.out.print(node.val + " ");
if (node.left != null) queue.add(node.left);
if (node.right != null) queue.add(node.right);
}
System.out.println(); // 每层换行
}
}
// 测试主方法：模拟普通二叉树、单支BST转平衡BST
public static void main(String[] args) {
// 1. 测试普通二叉树（无序结构）
TreeNode normalTree = new TreeNode(3);
normalTree.left = new TreeNode(1);
normalTree.right = new TreeNode(5);
normalTree.left.right = new TreeNode(2);
normalTree.right.left = new TreeNode(4);
// 2. 测试单支BST（右单支，极端不平衡）
TreeNode singleBranchBST = new TreeNode(1);
singleBranchBST.right = new TreeNode(2);
singleBranchBST.right.right = new TreeNode(3);
singleBranchBST.right.right.right = new TreeNode(4);
// ====== 转换普通二叉树为平衡BST ======
System.out.println("=== 普通二叉树转换为平衡BST ===");
// 步骤1：提取所有节点值
List<Integer> normalVals = extractValues(normalTree);
// 转成int数组（方便排序）
int[] normalArr = normalVals.stream().mapToInt(Integer::intValue).toArray();
// 步骤2：选择排序方法（可直接切换：quickSort/insertionSort/shellSort）
quickSort(normalArr);
System.out.println("排序后的数组：" + Arrays.toString(normalArr)); // 输出[1,2,3,4,5]
// 步骤3：构建平衡BST
TreeNode balancedNormalTree = sortedArrayToBalancedBST(normalArr);
System.out.println("普通树转换后BST结构（层序）：");
printBST(balancedNormalTree); // 输出平衡结构：3 → 1 4 → 2 5
// ====== 转换单支BST为平衡BST ======
System.out.println("\n=== 单支BST转换为平衡BST ===");
// 步骤1：单支BST用中序遍历获取有序数组（省排序步骤）
List<Integer> singleVals = new ArrayList<>();
inorderTraversal(singleBranchBST, singleVals); // 中序遍历单支BST，得到[1,2,3,4]
int[] singleArr = singleVals.stream().mapToInt(Integer::intValue).toArray();
System.out.println("中序遍历有序数组：" + Arrays.toString(singleArr));
// 步骤2：单支BST无需排序（直接用有序数组）
// 步骤3：构建平衡BST
TreeNode balancedSingleTree = sortedArrayToBalancedBST(singleArr);
System.out.println("单支BST转换后BST结构（层序）：");
printBST(balancedSingleTree); // 输出平衡结构：2 → 1 3 → 4
}
}
二，AVL树
2.1AVL树的概念
二叉搜索树虽可以缩短查找的效率，但如果数据有序或接近有序二叉搜索树将退化为单支树，查找元素相当于在顺 序表中搜索元素，效率低下 。因此，两位俄罗斯的数学家G.M.Adelson-Velskii和E.M.Landis在1962年 发明了一种 解决上述问题的方法：当向二叉搜索树中插入新结点后，如果能保证每个结点的左右子树高度之差的绝对值不超过 1(需要对树中的结点进行调整)，即可降低树的高度，从而减少平均搜索长度。
一棵AVL树或者是空树，或者是具有以下性质的二叉搜索树：
它的左右子树都是AVL树
左右子树高度之差(简称平衡因子)的绝对值不超过1(-1/0/1)
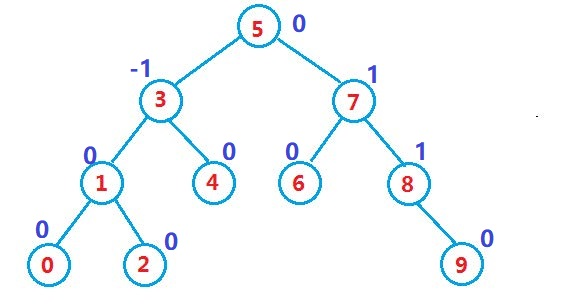
如果一棵二叉搜索树是高度平衡的，它就是AVL树。如果它有n个结点，其高度可保持在 ，搜索时间复杂 度O( )。
2.2 AVL树节点的定义
java
class AVLTreeNode{
public AVLTreeNode left=null;
public AVLTreeNode right=null;
public AVLTreeNode parent=null;
public int val=0;
public int bf=0;// 当前节点的平衡因子=右子树高度-左子树的高度
public AVLTreeNode(int val) {
this.val = val;
}
}2.3AVL树的插入与左右旋转
AVL树就是在二叉搜索树的基础上引入了平衡因子，因此AVL树也可以看成是二叉搜索树。那么AVL树的插入过程可 以分为两步。
1，按二叉搜索树的方式插入新节点
2，调整节点的平衡因子
java
public class AVLTree {
private AVLNode root; // AVL树根节点
// -------------------------- 旋转辅助方法 --------------------------
/**
* 右旋操作：以node为旋转中心（解决左左失衡）
* @param node 失衡的根节点（bf=-2）
*/
private void rightRotate(AVLNode node) {
AVLNode subL = node.left; // node的左孩子（旋转后成为新根）
AVLNode subLR = subL.right; // subL的右孩子（需要挂载到node的左子树）
// 步骤1：挂载subL的右孩子到node的左子树
node.left = subLR;
if (subLR != null) {
subLR.parent = node;
}
// 步骤2：处理subL的父节点（更新根/父节点的子节点引用）
subL.parent = node.parent;
if (node.parent == null) { // node是根节点
root = subL;
} else if (node == node.parent.left) { // node是父节点的左孩子
node.parent.left = subL;
} else { // node是父节点的右孩子
node.parent.right = subL;
}
// 步骤3：将node挂载到subL的右子树
subL.right = node;
node.parent = subL;
// 步骤4：重置平衡因子（旋转后子树高度恢复，bf归0）
node.bf = 0;
subL.bf = 0;
}
/**
* 左旋操作：以node为旋转中心（解决右右失衡）
* @param node 失衡的根节点（bf=2）
*/
private void leftRotate(AVLNode node) {
AVLNode subR = node.right; // node的右孩子（旋转后成为新根）
AVLNode subRL = subR.left; // subR的左孩子（需要挂载到node的右子树）
// 步骤1：挂载subR的左孩子到node的右子树
node.right = subRL;
if (subRL != null) {
subRL.parent = node;
}
// 步骤2：处理subR的父节点（更新根/父节点的子节点引用）
subR.parent = node.parent;
if (node.parent == null) { // node是根节点
root = subR;
} else if (node == node.parent.left) { // node是父节点的左孩子
node.parent.left = subR;
} else { // node是父节点的右孩子
node.parent.right = subR;
}
// 步骤3：将node挂载到subR的左子树
subR.left = node;
node.parent = subR;
// 步骤4：重置平衡因子
node.bf = 0;
subR.bf = 0;
}
// -------------------------- 插入核心方法 --------------------------
public boolean insert(int val) {
// 场景1：空树，直接插入根节点
if (root == null) {
root = new AVLNode(val);
return true;
}
// 场景2：非空树，先按二叉搜索树规则找插入位置
AVLNode parent = null;
AVLNode cur = root;
while (cur != null) {
if (cur.val == val) { // 重复值，插入失败
return false;
} else if (cur.val > val) { // 向左找
parent = cur;
cur = cur.left;
} else { // 向右找
parent = cur;
cur = cur.right;
}
}
// 创建新节点并挂载到父节点的左/右
cur = new AVLNode(val);
if (parent.val > val) {
parent.left = cur;
} else {
parent.right = cur;
}
cur.parent = parent;
// 场景3：插入后调整平衡因子 + 处理失衡（核心逻辑）
while (parent != null) {
// 第一步：更新父节点的平衡因子
if (cur == parent.left) {
parent.bf--; // 左子树插入，平衡因子-1
} else {
parent.bf++; // 右子树插入，平衡因子+1
}
// 第二步：根据平衡因子分情况处理
if (parent.bf == 0) {
// 情况1：插入前parent.bf=±1 → 插入后=0，子树高度不变，无需向上更新
break;
} else if (parent.bf == 1 || parent.bf == -1) {
// 情况2：插入前parent.bf=0 → 插入后=±1，子树高度+1，继续向上检查
cur = parent;
parent = cur.parent;
} else {
// 情况3：parent.bf=±2，子树失衡，需要旋转修复
if (parent.bf == -2) { // 左子树过高（最终需右旋）
if (cur.bf == -1) {
// 子情况1：左左失衡 → 直接右旋parent
rightRotate(parent);
} else {
// 子情况2：左右失衡 → 先左旋cur，再右旋parent
leftRotate(cur);
rightRotate(parent);
}
} else { // parent.bf=2，右子树过高（最终需左旋）
if (cur.bf == 1) {
// 子情况3：右右失衡 → 直接左旋parent
leftRotate(parent);
} else {
// 子情况4：右左失衡 → 先右旋cur，再左旋parent
rightRotate(cur);
leftRotate(parent);
}
}
// 旋转后子树高度恢复，无需继续向上更新
break;
}
}
return true;
}
}2.4AVL树的验证
1，验证其为二叉搜索树
如果中序遍历 可以得到一个有序的序列，就说明为二叉搜索树
2，验证其为平衡二叉树
每个节点子树高度差的绝对值不超过1
每个节点的平衡因子是否计算正确
java
private boolean isBalance(TreeNode root) {
if(root == null) return true;
int leftH = height(root.left);
int rightH = height(root.right);
//检查平衡因子
if(rightH - leftH != root.bf) {
System.out.println(root.val+" 平衡因子异常！");
return false;
}
return Math.abs(leftH-rightH) <= 1 &&
isBalance(root.left) && isBalance(root.right);
}
// 以node为根的子树的高度
private int height(AVLNode node) {
// 边界条件：空节点的高度记为-1（也有实现记为0，需和业务逻辑统一）
if (node == null) {
return -1;
}
// 递归计算：当前节点的高度 = 左右子树高度的较大值 + 1（自己占一层）
return Math.max(height(node.left), height(node.right)) + 1;
}2.5AVL树的删除（了解一下即可）
2.6AVL树性能
AVL树是一棵绝对平衡的二叉搜索树，其要求每个节点的左右子树高度差的绝对值都不超过1 ，这样可以保证查询 时高效的时间复杂度，即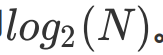 
。但是如果要对AVL树做一些结构修改的操作，性能非常低下，比如：插入时要 维护其绝对平衡，旋转的次数比较多，更差的是在删除时，有可能一直要让旋转持续到根的位置。因此：如果需要 一种查询高效且有序的数据结构，而且数据的个数为静态的(即不会改变)，可以考虑AVL树，但一个结构经常修 改，就不太适合。