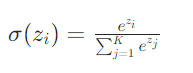前文介绍：前面我们以及介绍了自然语言序列输入到模型中进行的词嵌入和位置编码的数据变化过程，本文在前文的基础上继续接着解释编码器中的数据流动过程和编码器结构，阅读本文前最好参考前文：词嵌入和位置编码（超详细+图解）
https://blog.csdn.net/Drise_/article/details/155502880?fromshare=blogdetail&sharetype=blogdetail&sharerId=155502880&sharerefer=PC&sharesource=Drise_&sharefrom=from_link
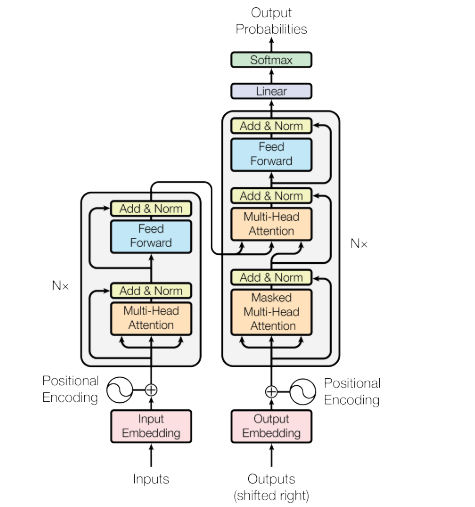
以下为***《Attention Is All You Need》*** 的transformer结构，本文会对编码器部分进行介绍：
1.Encoder Stacks（编码器堆栈）
首先我们关注到下图的Nx部分，它代表的编码器堆栈的堆叠层数，也就是有编码器堆栈的编码器数量。在论文***《Attention Is All You Need》***中，Nx =6,本文基于此进行介绍。
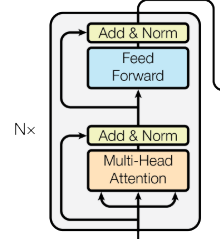
编码器层间串行
编码器层间串行的意思是，上面的6个编码器是以串行的方式进行数据流动的，堆栈中的第一个编码器从嵌入和位置编码中接收其输入。堆栈中的其他编码器从前一个编码器接收它们的输入，如下所示：
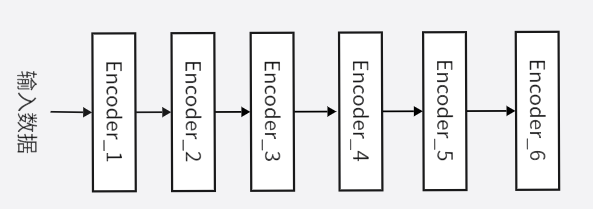
编码器层内并行处理数据
在每个编码器内部的 token 计算依然是并行的，如上图第一个编码器输入的数据就是一个token序列，不了解的朋友可以看看这篇文章：词嵌入和位置编码（超详细+图解）https://blog.csdn.net/Drise_/article/details/155502880?fromshare=blogdetail&sharetype=blogdetail&sharerId=155502880&sharerefer=PC&sharesource=Drise_&sharefrom=from_link
当编码器得到一个token序列，序列首先进入到一个多头注意力层，在这个注意力层，序列中的所有token都是并行处理的，然后将并行输出所有 token 的特征输入到前馈层，最后输出到下一个编码器，这也是transformer的核心优势，并行处理让它能够更加适配在GPU上进行运行，大大加快运行速度。
介绍了一下编码器堆栈中的数据处理大体过程，接下来我会介绍其具体部件。
2.编码器结构
编码器结构如下：
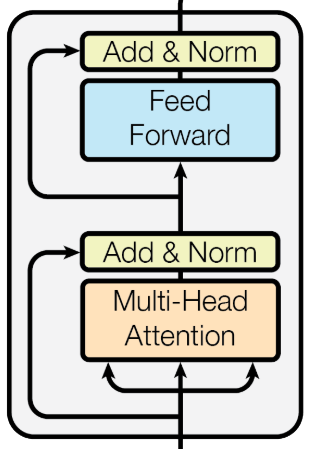
1.Multi-Head Attention(多头注意力层)
多头注意力是对基础自注意力的扩展优化，核心作用是让模型同时从不同维度 / 子空间捕捉序列中多样的依赖关系，提升注意力机制的表达能力和灵活性，我们要先讲讲自注意力的计算。
补充：自注意力和注意力的区别
自注意力是注意力机制的一种具体实现形式 ，注意力是更宽泛的技术框架，在注意力机制中Query、Key、Value 可来自不同数据源，而自注意力则是指**Query、Key、Value 来自同一数据源，**在编码器中我们计算的都是自注意力。
自注意力的计算
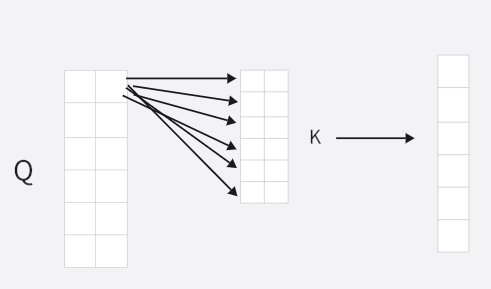
首先附上论文中的 缩放点积注意力图，如下：
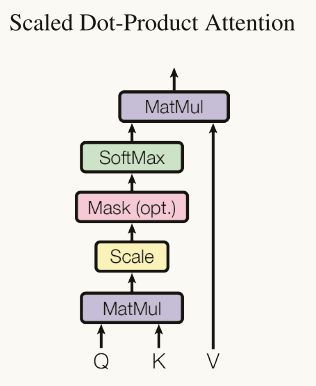
从图片我们可以看到***Q , K , V，***它们分别代表查询向量，键向量和值向量，他们是怎么生成的呢？
首先根据对于词嵌入和位置编码部分的讲解，我们举的例子已经进行到将词嵌入和位置编码叠加后输入编码器，如下：
我们可以知道此时我们的编码器输入维度为（1，6，2），在输入到自注意力层之前，我们要明确自注意力层中的三个权重矩阵 ，
，
，在自注意力层（可理解为单头自注意力层）中，这三个权重矩阵的维度是一模一样的，都是***（d_model,d_model）,***根据我们的例子，那我们生成的权重矩阵就是三个 2*2 的矩阵，因此我们知道
权重矩阵的维度只和模型维度 d_model 直接相关
在上面我们通过输入维度为（1，6，2）的输入向量和我们的三个权重矩阵 ，
，
分别相乘，（6，2）* （2，2） =（6，2） ，就可以得到三个（6，2）维度的矩阵，这三个矩阵就是这个序列对应的Q , K , V 向量， 其中每行代表对应token的Q , K , V 向量， 比如这三个矩阵的第一行分别代表这个token序列的第一个token的***Q , K , V 向量，***图例如下：
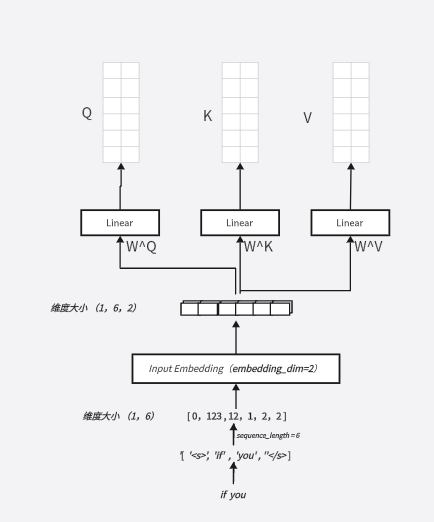
可以看到，在图中与权重矩阵相乘的操作我是使用线性层的来完成的，实际上在实际应用中也是如此，有人可以会好奇多批次时维度的变化，以下我做一点补充：
倘若我们是一个多批次的向量，假设为（3，6，2），不变的是权重矩阵
，
得到了Q ,K ,V，我们就可以继续前面的讨论
计算之前我们要明确自注意力得分的意义：自注意力得分的本质是当前 token 与序列中所有 token 的相似度，因此每个 token 会生成与序列长度一致的得分向量。
根据上图我们可以得到自注意力分数的计算方法：
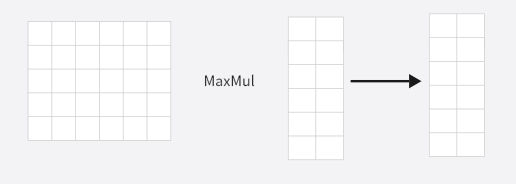
1.MatMul
序列每个token的键向量与当前token的查询向量进行内积，例如在上图进行第一个token的注意力分数计算时，就应该拿Q的第一行与K的每一行进行内积（MatMul），得到6个值，如下
上面例子的Q，K完成这些操作后面生成的矩阵维度为**（6，6）**
2.Scale
这一步的目的是减低得分，防止内积过大，具体操作是将前面得到的分数都除以根号下d_model
3.Mask
这里的（opt）表示这一步是可选的，不是必须的，这里我主要讲讲编码器中的Mask操作，编码器在计算注意力得分时仅使用 Padding Mask（填充掩码），核心目的是屏蔽输入序列中<pad>填充 token 对应的注意力得分，避免模型将无意义的填充内容纳入语义依赖计算。
具体的操作是：生成一个 Padding Mask 矩阵，它的维度与前面MatMul生成的矩阵的维度一模一样，也是（6，6），在这个矩阵中的元素取值规则是，非<pad>token位取值 0，<pad>的 token位取值为一个很大的负数。
得到相应的Padding Mask 矩阵如下：
然后将这个矩阵和前面得的MatMul生成的矩阵进行叠加，可以得到一个矩阵，它在<pad>对应的token位置上取值是一个很大的负数，相反则与原来的MatMul生成的矩阵值相同，这一步的目的是为了在接下来的softmax归一化处理中屏蔽输入序列中<pad>填充 token 对应的注意力得分
4.SoftMax
对原来的注意力分数进行softmax可以得到softmax分数，
这一步操作相信大家已经有所了解了，这里我直接贴出公式：
在这里我们就能知道了，<pad>位置的token值接近负无穷，得到的softmax分数就是0
这样就**屏蔽输入序列中<pad>填充 token 对应的注意力得分，**同时softmax还可以对非<pad>位置的分数进行归一化处理。
5.MatMul
这一步的操作是将前面得到的softmax分数与每个token的值向量进行点积，得到自注意力层在对应token位置上的输出，最终得到一个Z矩阵，以前面举例，结果如下：
有人可能会好奇，这样的点积值向量不是按行了，而是按列被乘了（乘进去的 V 向量包含了整个序列所有 token 的特征向量），这里这样做的原因是这里的 "点积" 并非严格数学意义上的 "向量点积"，本质是按权重对 Value 进行加权求和，最终得到每个 token 的融合后特征 。
接下来附上论文中自注意力的计算公式就很容易理解了：
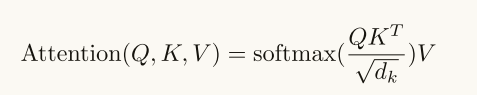
总结：注意力分数的核心意义是量化 "当前 token 与序列中所有其他 token 的关联强度"，本质是 "相似度评分"------ 分数越高，代表两个 token 的语义 / 结构关联越紧密，是模型判断 "该重点关注哪些 token 信息" 的直接依据。
在自注意力层中Query 和 Key 之间的点积用来计算出每对词之间的相关性。然后，这种相关性被用作一个 "因子 "来计算所有 Value 向量的加权和，该加权和的输出为注意力分数。
扩展到多头注意力层
多头注意力的核心要求是 :
模型特征维度 d_model 必须能被头数 h 整除（即 dmodel%h==0）
多头注意力层的核心意义是让模型并行学习多个不同维度的 token 关联模式，相当于给模型配备了 "多组不同的注意力探测器"，能捕捉到更丰富、更细粒度的语义 / 结构依赖，相比单头注意力大幅提升特征表达能力。 举例来说就是观察这么一个句子 "我在寝室打游戏", 单头可以就关注到了我打游戏，但是多头就不一样了，一个头关注到我在打游戏，一个头关注到我在宿舍，这样我们获取到的语义是不是更加丰富呢。
多头注意力层的实现相较于单头自注意力层，在权重矩阵上的没有变化 ，拆分的是权重矩阵的输出（Q/K/V）**，不是权重矩阵本身。前文我们讲到了输入向量于权重矩阵的点积我们是通过线性层实现的，现在变成多头注意力层，但是实际上的结构是不变的：
补充：使用同样的权重矩阵，多头和单头的区别在哪里？
其实这里的区别主要是后面的拆分 K,Q,V 矩阵导致的，多头比单头强的关键在于单头没有 "拼接 + 线性融合" ，多头使用主题 K,Q,V 矩阵计算得分，相对于从一个角度看问题，而多头将K,Q,V矩阵拆分为头数份，再分别计算分数，并且后续进行"拼接 + 线性融合"，相对于从多个角度看问题。
事实上我们还是维持原来的结构，如下：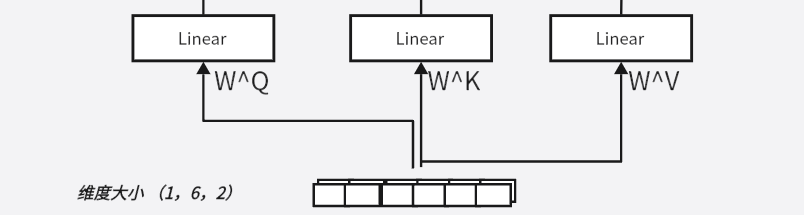
那么我们如何拆分***（Q/K/V）*** ，我们假设我们是二头自注意力层， 我们知道权重矩阵的维度是（2，2），那么在多头自注意力层中的权重矩阵**按列进行拼接，**得到的Q V K矩阵如下：
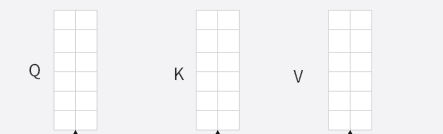
拆分规则：Q、K、V 的拆分是沿特征维度（最后一维）的均等分割
像上面的Q,V,K三个矩阵按照最后一维进行拆分为头数份如下所示：
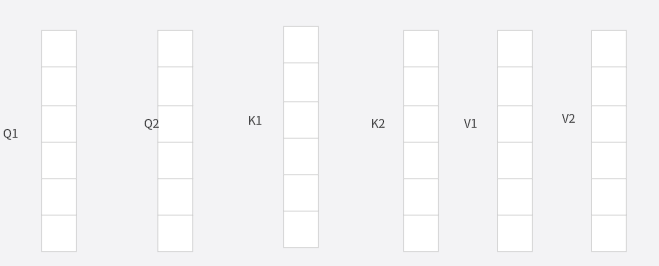
接下来按照单头注意力分数计算的步骤进行 ，最终可以得到二个Z矩阵，如下
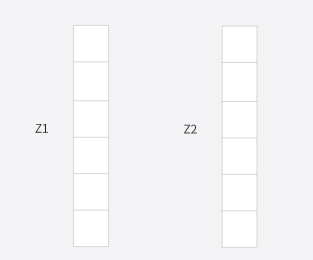
如何我们将这些Z矩阵按列拼接到一起，得到下面的矩阵：
然后我们再通过一个线性层，这个线性层的作用是线性融合，它的权重矩阵我们称为 ,它的形状和
，
，
一模一样，在我的例子中是（2，2），拼接后的Z矩阵乘上
，得到（6，2)维度的最终得分矩阵：
总结：多头自注意力层的权重矩阵
2.Feed Forward（前馈层）和 Add & Norm
先粘贴一下编码器结构，前面离得太远了
Feed Forward 和 Add & Norm比较简单，这里直接归纳为一小节。
首先是两个Add & Norm ，其中Add指的是残差连接，它的作用是保留原始信息 + 缓解梯度消失 他是如何保留原始信息的呢，假设输入数据为 X（维度 (1,6,2)）， 多头注意力输出 Z（维度 (1,6,2)）那么Add 后即为将这两个进行叠加，为 X + Z， 为什么残差连接可以达到这种作用的，这里不多讲，大家可以去了解一下 ResNet 。
然后是Norm，Norm指的是层归一化操作，它对 Add 后的特征做 "逐样本、逐特征维度" 的归一化，让每个 token 的特征分布保持稳定（均值≈0，方差≈1），这样的作用是抑制异常值，加快收敛。
最后是前馈层Feed Forward ，这里的前馈层其实是一个双层的全连接层，其中有两个线性层， 它主要是让数据完成升维→非线性激活→降维的操作，核心作用是 "深化单个 token 的特征表达"------ 与多头注意力层的 "捕捉全局 token 关联" 形成互补，通过 "升维→非线性激活→降维" 的固定结构，让模型学到更复杂的特征模式。
首先是升维，论文是让d_model升到它的四倍。对应到我们前面得到的（1，6，2）的输出，就是要变成维度为（1，6，8）的维度，在线性层让输入进行升维是很简单的，主要让权重矩阵维度为（2，8），就可以完成升维到目的的维度，至于偏置为一维张量，长度为8
然后是非线性激活，这里使用ReLu函数进行非线性激活。
最后是降维，要降到输入的维度，对应到我们前面得到的（1，6，8）的输出，就是要变成维度为（1，6，2）的维度，在线性层让输入进行升维是很简单的，主要让权重矩阵维度为（8，2），就可以完成升维到目的的维度，至于偏置为一维张量，长度为2
这是本人自己总结出的学习记录，若有错误，欢迎一起讨论交流。