【算法基础篇】（二十六）数据结构封神！Trie 树从入门到爆杀算法题：拼音输入法、单词统计都靠它

目录

前言

[一、先搞懂：Trie 树到底是个啥？](#一、先搞懂：Trie 树到底是个啥？)

[1.1 从 "查字典" 理解 Trie 树](#1.1 从 “查字典” 理解 Trie 树)

[1.2 Trie 树的 "超能力"：为什么它比哈希、数组更牛？](#1.2 Trie 树的 “超能力”：为什么它比哈希、数组更牛？)

[1.3 Trie 树的核心应用场景](#1.3 Trie 树的核心应用场景)

[二、手把手实现：Trie 树的核心操作（C++ 代码）](#二、手把手实现：Trie 树的核心操作（C++ 代码）)

[2.1 Trie 树的节点结构设计](#2.1 Trie 树的节点结构设计)

[2.2 核心操作 1：插入字符串](#2.2 核心操作 1：插入字符串)

[2.3 核心操作 2：查询字符串出现次数](#2.3 核心操作 2：查询字符串出现次数)

[2.4 核心操作 3：查询前缀相同的字符串个数](#2.4 核心操作 3：查询前缀相同的字符串个数)

[2.5 基础功能测试：验证 Trie 树是否工作](#2.5 基础功能测试：验证 Trie 树是否工作)

[三、进阶功能：处理大小写字母 + 数字（通用 Trie 树）](#三、进阶功能：处理大小写字母 + 数字（通用 Trie 树）)

[3.1 字符转路径编号：get_num 函数](#3.1 字符转路径编号：get_num 函数)

[3.2 通用 Trie 树实现代码](#3.2 通用 Trie 树实现代码)

[四、实战刷题：洛谷经典 Trie 树题目（AC 代码）](#四、实战刷题：洛谷经典 Trie 树题目（AC 代码）)

[4.1 题目 1：洛谷 P8306 【模板】字典树](#4.1 题目 1：洛谷 P8306 【模板】字典树)

[4.2 题目 2：洛谷 P2580 于是他错误的点名开始了](#4.2 题目 2：洛谷 P2580 于是他错误的点名开始了)

[4.3 题目 3：洛谷 P10471 最大异或对](#4.3 题目 3：洛谷 P10471 最大异或对)

[五、避坑指南：Trie 树常见问题与优化](#五、避坑指南：Trie 树常见问题与优化)

[5.1 坑点 1：数组大小不够导致越界](#5.1 坑点 1：数组大小不够导致越界)

[5.2 坑点 2：输入输出未加速导致超时](#5.2 坑点 2：输入输出未加速导致超时)

[5.3 坑点 3：字符处理错误（大小写、特殊字符）](#5.3 坑点 3：字符处理错误（大小写、特殊字符）)

[5.4 坑点 4：多组测试数据未初始化](#5.4 坑点 4：多组测试数据未初始化)

[5.5 优化：空间优化（压缩节点）](#5.5 优化：空间优化（压缩节点）)

总结

---

前言

你有没有想过，为什么手机输入法输入 "ha" 能瞬间跳出 "哈""哈罗""哈喽"？为什么搜索引擎输入 "alg" 能自动联想 "algorithm""algorithms"？这些看似神奇的功能，背后都离不开一个叫Trie 树的数据结构。它就像一个 "字符串字典"，能把字符串按公共前缀打包存储，查词、补全、统计效率直接拉满，是处理字符串前缀问题的 "天花板" 级工具。

不管你是刚接触数据结构的新手，还是正在备战面试的 "刷题党"，Trie 树都是必学知识点。这篇文章从原理、实现到实战，用最通俗的语言 + 可直接运行的 C++ 代码，带你彻底搞懂 Trie 树，看完就能上手解决实际问题！下面就让我们正式开始吧！

---

一、先搞懂：Trie 树到底是个啥？

在正式敲代码之前，我们先解决一个核心问题：Trie 树到底是什么？它为什么能这么高效？

1.1 从 "查字典" 理解 Trie 树

你平时查纸质字典时，会怎么找 "apple" 这个单词？不会从第一页逐字翻，而是先找以 "a" 开头的部分，再在 "a" 下面找 "p"，接着在 "ap" 下面找 "p"，一步步缩小范围 ------ 这就是 Trie 树的核心思想：按公共前缀分层存储。

Trie 树（也叫字典树、前缀树）是一种专门处理字符串的树形数据结构，它的每个节点代表一个字符，从根节点到某个叶子节点的路径，就对应一个完整的字符串。比如存储 "apple""app""banana""bat" 这四个单词，Trie 树会长这样：

• 根节点（无字符）下面分两支："a" 和 "b"；
• "a" 下面接 "p"，"p" 下面再接 "p"（此时路径 "a→p→p" 对应 "app"）；
• "app" 下面继续接 "l"，再接 "e"（路径 "a→p→p→l→e" 对应 "apple"）；
• "b" 下面分两支："a"（对应 "banana" 的前缀）和 "a"（对应 "bat" 的前缀），后续再按字符延伸。

再如存储"abc"、"abd"、"acde"以及""cd"时：

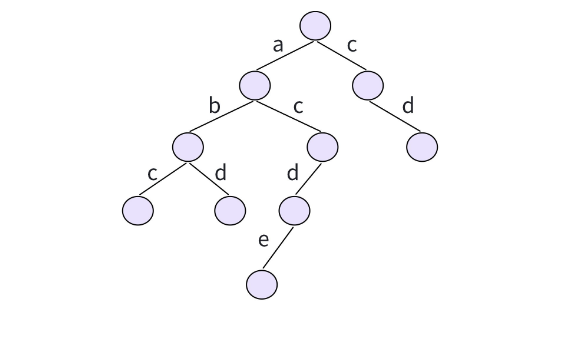
这样一来，所有有公共前缀的字符串都会共享一条路径，既节省空间，又能快速定位。

1.2 Trie 树的 "超能力"：为什么它比哈希、数组更牛？

可能有同学会问：用哈希表存字符串也能快速查询，为什么非要用 Trie 树？我们用一组对比说话：

数据结构	查找单个字符串	统计前缀相同的字符串	前缀补全（如输入法）	空间效率（公共前缀多）
普通数组	O(n*m)	O(n*m)	无法实现	差（重复存储公共前缀）
哈希表	O (1)（理想）	O(n)	无法实现	中（无公共前缀优化）
Trie 树	O (k)（k 为字符串长度）	O(k)	轻松实现	优（共享公共前缀）

比如要统计 "app""apple""apply" 这三个单词的个数，Trie 树只要找到 "a→p→p" 这条路径，就能直接获取所有以 "app" 为前缀的字符串，而哈希表需要遍历所有键才能统计 ------ 这就是 Trie 树在 "前缀相关问题" 中的绝对优势。

1.3 Trie 树的核心应用场景

Trie 树不是 "万能药"，但在以下场景中堪称 "神器"：

1. 字符串查询：判断一个单词是否在字典中（如拼写检查）
2. 前缀统计：统计有多少个单词以某个字符串为前缀（如统计 "app" 开头的单词数）
3. 前缀补全：根据输入的前缀，补全所有可能的字符串（如输入法、搜索引擎联想）
4. 最大异或对：将数字转为二进制，用 Trie 树找异或最大值（算法竞赛高频题）
5. 单词频率统计：记录每个单词出现的次数（如文本词频分析）

接下来，我们就从最基础的 Trie 树实现开始，一步步掌握这些功能。

二、手把手实现：Trie 树的核心操作（C++ 代码）

Trie 树的实现主要围绕三个核心操作：插入字符串 、查询字符串出现次数 、查询前缀相同的字符串个数。我们先定义 Trie 树的节点结构，再逐一实现这些操作。

2.1 Trie 树的节点结构设计

Trie 树的每个节点需要存储两个关键信息：

1. 子节点指针数组：比如处理小写字母，每个节点有 26 个指针（对应 a-z），表示当前节点的下一个字符可能是哪一个。
2. 计数信息 ：
   • p[cur]：表示经过当前节点的字符串个数（用于统计前缀相同的字符串）
   • e[cur]：表示以当前节点为结尾的字符串个数（用于统计单词出现次数）

另外，我们用一个idx变量来给每个节点分配唯一编号，相当于 "节点的身份证"，方便管理子节点指针。

2.2 核心操作 1：插入字符串

插入字符串的逻辑很简单：从根节点（编号 0）开始，逐个字符遍历字符串，为每个字符创建对应的子节点（如果不存在），然后更新p数组（经过当前节点的次数 + 1），最后在字符串的最后一个字符节点处，更新e数组（以当前节点结尾的次数 + 1）。

比如插入 "apple"：

1. 根节点（0）→ 找 "a" 对应的子节点（假设不存在，创建节点 1），p[1] +=1
2. 节点 1 → 找 "p" 对应的子节点（创建节点 2），p[2] +=1
3. 节点 2 → 找 "p" 对应的子节点（创建节点 3），p[3] +=1
4. 节点 3 → 找 "l" 对应的子节点（创建节点 4），p[4] +=1
5. 节点 4 → 找 "e" 对应的子节点（创建节点 5），p[5] +=1
6. 最后，e[5] +=1（表示 "apple" 这个单词在这里结束）

插入操作代码：

#include <iostream>
#include <string>
#include <cstring>
using namespace std;

// 定义Trie树的全局参数
const int N = 1e6 + 10;  // 最大节点数（根据题目调整，1e6足够应对大多数场景）
int tr[N][26];           // 子节点指针数组：tr[cur][path]表示cur节点的path路径（0-25对应a-z）的子节点编号
int p[N];                // p[cur]：经过cur节点的字符串个数（前缀统计用）
int e[N];                // e[cur]：以cur节点为结尾的字符串个数（单词计数用）
int idx;                 // 节点编号计数器（从0开始，根节点编号为0）

// 初始化Trie树（多组测试数据时需要调用）
void init_trie() {
    memset(tr, 0, sizeof tr);  // 清空子节点指针
    memset(p, 0, sizeof p);    // 清空前缀计数
    memset(e, 0, sizeof e);    // 清空单词计数
    idx = 0;                   // 重置节点编号
}

// 插入字符串s到Trie树中
void insert(string& s) {
    int cur = 0;  // 从根节点开始
    p[cur]++;     // 根节点被经过一次（所有字符串都经过根节点）
    for (char ch : s) {
        int path = ch - 'a';  // 将字符转为路径编号（a→0，b→1，...，z→25）
        if (tr[cur][path] == 0) {  // 如果当前路径没有子节点，创建新节点
            tr[cur][path] = ++idx;
        }
        cur = tr[cur][path];  // 移动到子节点
        p[cur]++;             // 经过当前节点的次数+1
    }
    e[cur]++;  // 字符串结束，当前节点的单词计数+1
}

2.3 核心操作 2：查询字符串出现次数

查询字符串出现次数的逻辑：从根节点开始，逐个字符遍历字符串，如果某个字符对应的子节点不存在，说明字符串不在 Trie 树中，返回 0；如果遍历完所有字符，返回e[cur]（以当前节点结尾的字符串个数）。

比如查询 "apple"：

• 根节点→"a"（节点 1）→"p"（节点 2）→"p"（节点 3）→"l"（节点 4）→"e"（节点 5）
• 遍历完成，返回e[5]（即 "apple" 出现的次数）

如果查询 "apples"：

• 遍历到 "e"（节点 5）后，下一步找 "s" 对应的子节点，发现不存在，返回 0

查询操作代码：

// 查询字符串s在Trie树中出现的次数
int query_count(string& s) {
    int cur = 0;  // 从根节点开始
    for (char ch : s) {
        int path = ch - 'a';
        if (tr[cur][path] == 0) {  // 没有对应的子节点，字符串不存在
            return 0;
        }
        cur = tr[cur][path];       // 移动到子节点
    }
    return e[cur];  // 返回以当前节点结尾的字符串个数
}

2.4 核心操作 3：查询前缀相同的字符串个数

查询前缀相同的字符串个数，其实就是统计 "经过前缀最后一个字符对应的节点" 的次数，也就是p[cur]。

比如查询以 "app" 为前缀的字符串个数：

1. 根节点→"a"（节点 1）→"p"（节点 2）→"p"（节点 3）；
2. 遍历完成，返回p[3]（所有经过节点 3 的字符串，都是以 "app" 为前缀的）。

前缀查询代码：

// 查询有多少个字符串以s为前缀
int query_prefix(string& s) {
    int cur = 0;  // 从根节点开始
    for (char ch : s) {
        int path = ch - 'a';
        if (tr[cur][path] == 0) {  // 没有对应的子节点，前缀不存在
            return 0;
        }
        cur = tr[cur][path];       // 移动到子节点
    }
    return p[cur];  // 返回经过当前节点的字符串个数（即前缀相同的个数）
}

2.5 基础功能测试：验证 Trie 树是否工作

我们用一个简单的测试案例，验证插入、查询、前缀统计这三个功能是否正常：

int main() {
    init_trie();  // 初始化Trie树
    
    // 插入几个字符串
    string s1 = "apple";
    string s2 = "app";
    string s3 = "apply";
    string s4 = "banana";
    insert(s1);
    insert(s2);
    insert(s3);
    insert(s1);  // 再插入一次"apple"，次数变为2
    
    // 测试查询字符串出现次数
    cout << "apple出现次数：" << query_count(s1) << endl;  // 输出2
    cout << "app出现次数：" << query_count(s2) << endl;    // 输出1
    cout << "banana出现次数：" << query_count(s4) << endl;// 输出1
    cout << "orange出现次数：" << query_count(string("orange")) << endl;  // 输出0
    
    // 测试前缀统计
    cout << "以app为前缀的字符串个数：" << query_prefix(string("app")) << endl;  // 输出3（app、apple、apply）
    cout << "以ban为前缀的字符串个数：" << query_prefix(string("ban")) << endl;  // 输出1（banana）
    cout << "以ora为前缀的字符串个数：" << query_prefix(string("ora")) << endl;  // 输出0
    
    return 0;
}

运行结果：

apple出现次数：2
app出现次数：1
banana出现次数：1
orange出现次数：0
以app为前缀的字符串个数：3
以ban为前缀的字符串个数：1
以ora为前缀的字符串个数：0

完全符合预期！这说明我们的基础 Trie 树实现是正确的。

三、进阶功能：处理大小写字母 + 数字（通用 Trie 树）

前面的代码只处理小写字母，但实际场景中，字符串可能包含大写字母（如 "Fusu""AFakeFusu"）和数字（如 "998244353"）。我们需要扩展 Trie 树的节点结构，支持 62 种字符（26 小写 + 26 大写 + 10 数字）。

3.1 字符转路径编号：get_num 函数

首先实现一个get_num函数，将不同类型的字符转为唯一的路径编号：

• 小写字母（a-z）：0-25
• 大写字母（A-Z）：26-51（A→26，B→27，...，Z→51）
• 数字（0-9）：52-61（0→52，1→53，...，9→61）

3.2 通用 Trie 树实现代码

#include <iostream>
#include <string>
#include <cstring>
using namespace std;

const int N = 3e6 + 10;  // 节点数扩大，应对更长的字符串
int tr[N][62];           // 路径数改为62（26+26+10）
int p[N];                // 前缀计数
int e[N];                // 单词计数
int idx;                 // 节点编号

// 字符转路径编号（支持小写、大写、数字）
int get_num(char ch) {
    if (ch >= 'a' && ch <= 'z') {
        return ch - 'a';          // 小写字母：0-25
    } else if (ch >= 'A' && ch <= 'Z') {
        return ch - 'A' + 26;     // 大写字母：26-51
    } else {
        return ch - '0' + 52;     // 数字：52-61
    }
}

// 初始化Trie树
void init_trie() {
    memset(tr, 0, sizeof tr);
    memset(p, 0, sizeof p);
    memset(e, 0, sizeof e);
    idx = 0;
}

// 插入字符串（支持大小写+数字）
void insert(string& s) {
    int cur = 0;
    p[cur]++;
    for (char ch : s) {
        int path = get_num(ch);
        if (tr[cur][path] == 0) {
            tr[cur][path] = ++idx;
        }
        cur = tr[cur][path];
        p[cur]++;
    }
    e[cur]++;
}

// 查询字符串出现次数
int query_count(string& s) {
    int cur = 0;
    for (char ch : s) {
        int path = get_num(ch);
        if (tr[cur][path] == 0) {
            return 0;
        }
        cur = tr[cur][path];
    }
    return e[cur];
}

// 查询前缀相同的字符串个数
int query_prefix(string& s) {
    int cur = 0;
    for (char ch : s) {
        int path = get_num(ch);
        if (tr[cur][path] == 0) {
            return 0;
        }
        cur = tr[cur][path];
    }
    return p[cur];
}

// 测试通用Trie树
int main() {
    init_trie();
    
    string s1 = "Fusu";
    string s2 = "fusu";
    string s3 = "AFakeFusu";
    string s4 = "998244353";
    insert(s1);
    insert(s2);
    insert(s3);
    insert(s4);
    
    // 测试大小写敏感
    cout << "Fusu出现次数：" << query_count(s1) << endl;  // 1
    cout << "fusu出现次数：" << query_count(s2) << endl;  // 1
    // 测试数字
    cout << "998244353出现次数：" << query_count(s4) << endl;  // 1
    // 测试前缀
    cout << "以Fu为前缀的个数：" << query_prefix(string("Fu")) << endl;  // 1（Fusu）
    cout << "以A为前缀的个数：" << query_prefix(string("A")) << endl;    // 1（AFakeFusu）
    
    return 0;
}

运行结果：

Fusu出现次数：1
fusu出现次数：1
998244353出现次数：1
以Fu为前缀的个数：1
以A为前缀的个数：1

完美支持大小写和数字！这个通用版本的 Trie 树，能应对大多数实际场景。

四、实战刷题：洛谷经典 Trie 树题目（AC 代码）

理论学得差不多了，我们来刷两道洛谷的经典题目，巩固知识点。这些题目都是算法竞赛中的高频题，掌握了就能举一反三。

4.1 题目 1：洛谷 P8306 【模板】字典树

题目链接：https://www.luogu.com.cn/problem/P8306

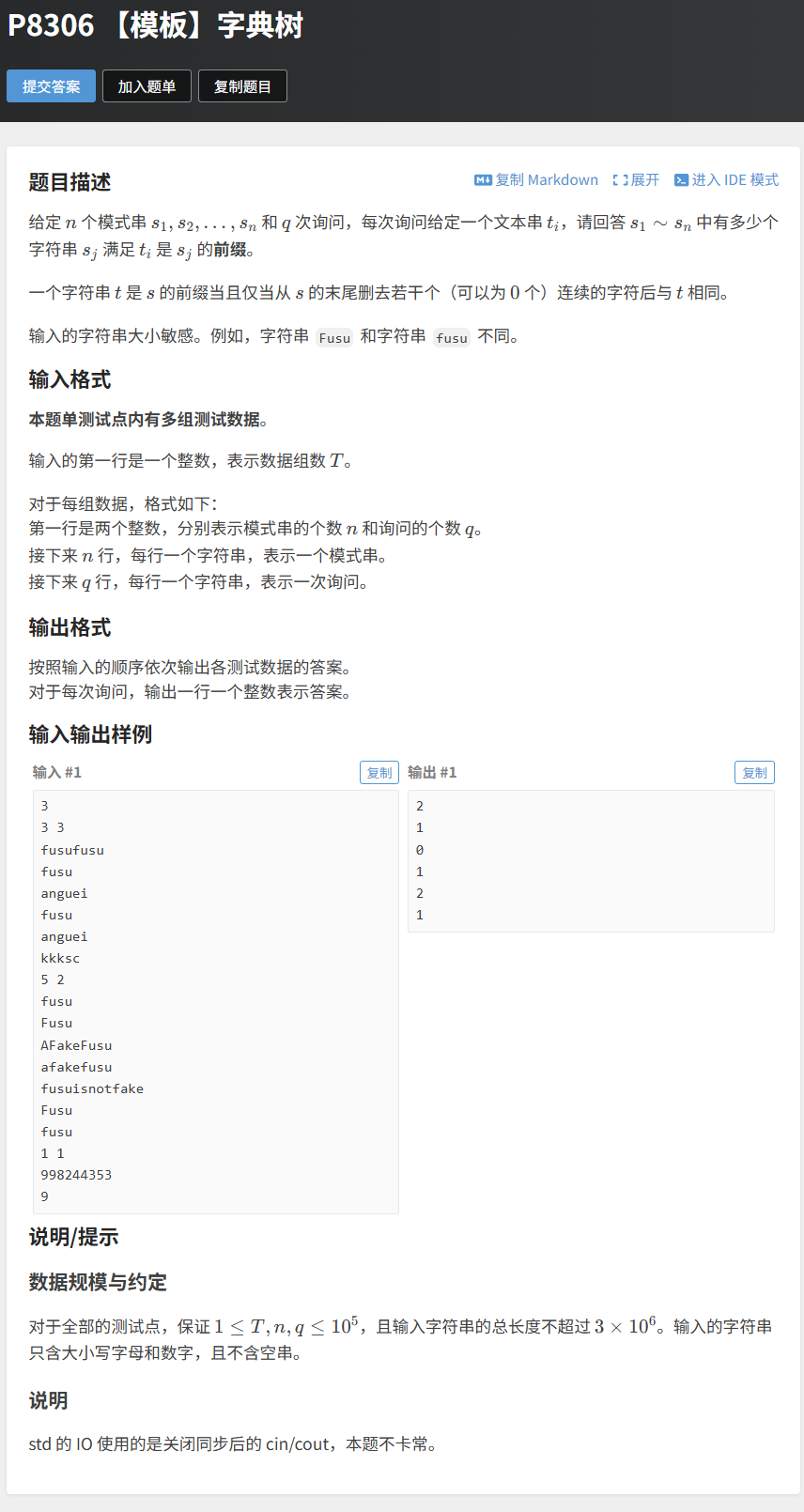
题目描述：给定 n 个模式串和 q 次询问，每次询问一个文本串 t，回答有多少个模式串以 t 为前缀（大小写敏感）。

解题思路：这是 Trie 树的经典前缀统计问题，直接用我们实现的 "通用 Trie 树" 即可：

1. 插入所有模式串到 Trie 树中；
2. 每次询问时，调用query_prefix函数，输出结果。

AC 代码：

#include <iostream>
#include <string>
#include <cstring>
using namespace std;

const int N = 3e6 + 10;
int tr[N][62];
int p[N];
int idx;

int get_num(char ch) {
    if (ch >= 'a' && ch <= 'z') return ch - 'a';
    else if (ch >= 'A' && ch <= 'Z') return ch - 'A' + 26;
    else return ch - '0' + 52;
}

void init_trie() {
    // 多组测试数据，用循环清空（memset效率低，适合小规模）
    for (int i = 0; i <= idx; i++) {
        memset(tr[i], 0, sizeof tr[i]);
        p[i] = 0;
    }
    idx = 0;
}

void insert(string& s) {
    int cur = 0;
    p[cur]++;
    for (char ch : s) {
        int path = get_num(ch);
        if (tr[cur][path] == 0) tr[cur][path] = ++idx;
        cur = tr[cur][path];
        p[cur]++;
    }
}

int query_prefix(string& s) {
    int cur = 0;
    for (char ch : s) {
        int path = get_num(ch);
        if (tr[cur][path] == 0) return 0;
        cur = tr[cur][path];
    }
    return p[cur];
}

int main() {
    ios::sync_with_stdio(false);
    cin.tie(0);  // 加速输入输出，避免超时
    
    int T;
    cin >> T;
    while (T--) {
        init_trie();
        int n, q;
        cin >> n >> q;
        // 插入n个模式串
        while (n--) {
            string s;
            cin >> s;
            insert(s);
        }
        // 处理q次询问
        while (q--) {
            string t;
            cin >> t;
            cout << query_prefix(t) << endl;
        }
    }
    return 0;
}

注意点：

• 题目有多组测试数据，init_trie函数用循环清空节点（memset对大数组效率低，容易超时）。
• 输入数据量大时，必须用ios::sync_with_stdio(false); **cin.tie(0);**加速输入输出，否则会超时。

4.2 题目 2：洛谷 P2580 于是他错误的点名开始了

题目链接：https://www.luogu.com.cn/problem/P2580

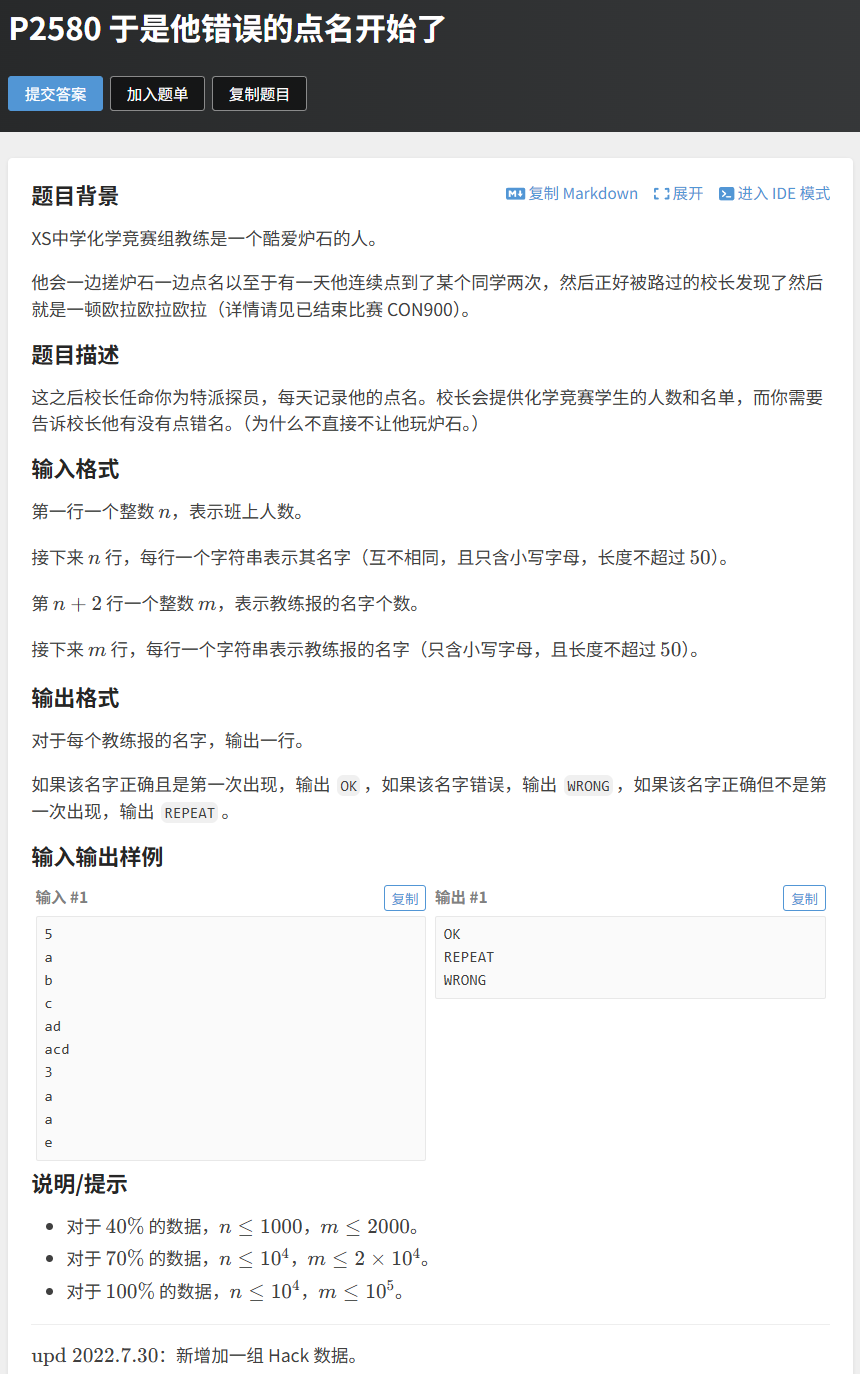
题目描述：给定 n 个学生的名字（互不相同），然后有 m 次点名，每次点名一个名字：

• 如果名字存在且是第一次被点，输出 "OK"
• 如果名字存在但已被点过，输出 "REPEAT"
• 如果名字不存在，输出 "WRONG"

解题思路 ：利用 Trie 树的e数组记录单词出现次数，查询时额外处理 "是否已被点过"：

1. 插入所有学生名字到 Trie 树中（**e[cur]**初始为 1，因为名字互不相同）
2. 每次查询时，若e[cur] == 1：输出 "OK"，并将**e[cur]**改为 - 1（标记为已点过）
3. 若e[cur] == -1：输出 "REPEAT"
4. 若e[cur] == 0：输出 "WRONG"

AC 代码：

#include <iostream>
#include <string>
#include <cstring>
using namespace std;

const int N = 5e5 + 10;  // 名字长度不超过50，n不超过1e4，5e5足够
int tr[N][26];
int e[N];  // e[cur]：1=未点过，-1=已点过，0=不存在
int idx;

void init_trie() {
    memset(tr, 0, sizeof tr);
    memset(e, 0, sizeof e);
    idx = 0;
}

void insert(string& s) {
    int cur = 0;
    for (char ch : s) {
        int path = ch - 'a';
        if (tr[cur][path] == 0) tr[cur][path] = ++idx;
        cur = tr[cur][path];
    }
    e[cur] = 1;  // 初始标记为未点过
}

int query(string& s) {
    int cur = 0;
    for (char ch : s) {
        int path = ch - 'a';
        if (tr[cur][path] == 0) return 0;  // 名字不存在
        cur = tr[cur][path];
    }
    if (e[cur] == 1) {
        e[cur] = -1;  // 标记为已点过
        return 1;     // 第一次点
    } else if (e[cur] == -1) {
        return -1;    // 重复点
    } else {
        return 0;     // 不存在（理论上不会走到这，因为插入时e[cur]设为1）
    }
}

int main() {
    ios::sync_with_stdio(false);
    cin.tie(0);
    
    init_trie();
    int n, m;
    cin >> n;
    // 插入n个学生名字
    while (n--) {
        string s;
        cin >> s;
        insert(s);
    }
    // 处理m次点名
    cin >> m;
    while (m--) {
        string s;
        cin >> s;
        int res = query(s);
        if (res == 1) {
            cout << "OK" << endl;
        } else if (res == -1) {
            cout << "REPEAT" << endl;
        } else {
            cout << "WRONG" << endl;
        }
    }
    return 0;
}

测试用例：

输入：

5
a
b
c
ad
acd
3
a
a
e

输出：

OK
REPEAT
WRONG

完全符合题目要求！

4.3 题目 3：洛谷 P10471 最大异或对

题目链接：https://www.luogu.com.cn/problem/P10471

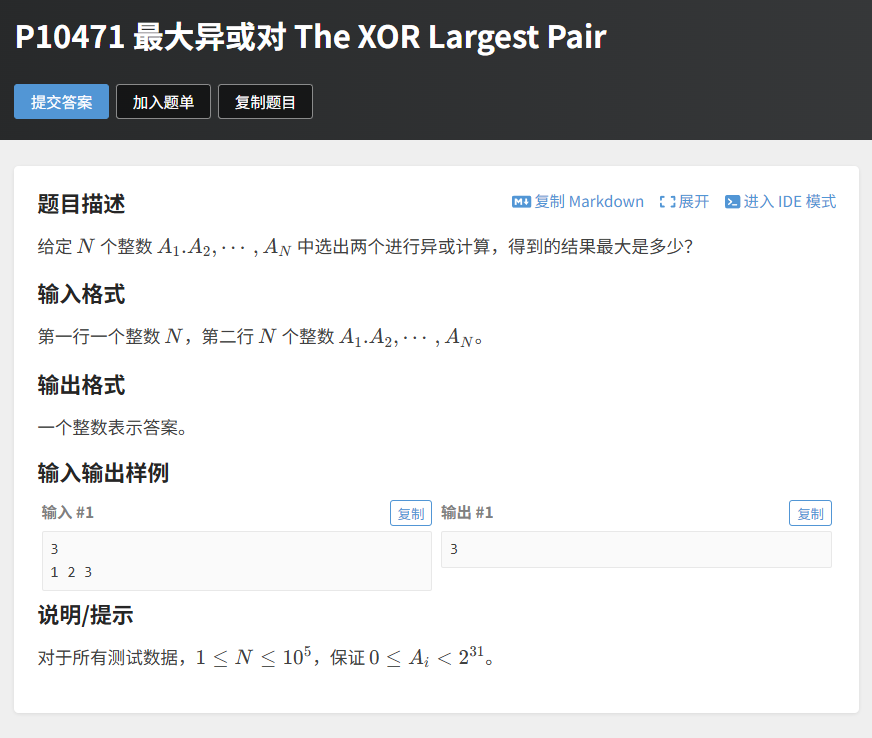
题目描述：给定 n 个整数，选出两个数进行异或运算，求结果的最大值。

解题思路：

这是 Trie 树的 "非字符串" 应用 ------ 将整数转为 32 位二进制（从高位到低位），用 Trie 树存储二进制位，然后对每个数，在 Trie 树中找 "每一位尽可能相反" 的数（异或最大值的核心是高位不同）。

比如数字 3（二进制 11）和数字 1（二进制 01）：

• 3 的二进制是 11，找相反的位：第一位（最高位）找 0，第二位找 0；
• 1 的二进制是 01，第一位是 0（与 3 的 1 相反），第二位是 1（与 3 的 1 相同），异或结果是 10（2）；
• 但如果有数字 0（二进制 00），与 3 异或结果是 11（3），更大。

AC 代码：

#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;

const int N = 1e5 + 10;
int tr[N * 32][2];  // 每个整数32位，n=1e5，所以节点数1e5*32=3.2e6
int idx;

// 初始化Trie树
void init_trie() {
    memset(tr, 0, sizeof tr);
    idx = 0;
}

// 插入一个整数的二进制到Trie树（从高位到低位）
void insert(int x) {
    int cur = 0;
    for (int i = 31; i >= 0; i--) {  // 32位整数，从最高位（31位）开始
        int bit = (x >> i) & 1;      // 取第i位的二进制值（0或1）
        if (tr[cur][bit] == 0) {
            tr[cur][bit] = ++idx;
        }
        cur = tr[cur][bit];
    }
}

// 找与x异或最大的数，返回异或结果
int find_max_xor(int x) {
    int cur = 0;
    int res = 0;
    for (int i = 31; i >= 0; i--) {
        int bit = (x >> i) & 1;
        // 贪心策略：优先找与当前bit相反的位（异或结果为1，更大）
        if (tr[cur][1 - bit] != 0) {
            res |= (1 << i);  // 第i位异或结果为1，加入res
            cur = tr[cur][1 - bit];
        } else {
            // 没有相反的位，只能找相同的位（异或结果为0）
            cur = tr[cur][bit];
        }
    }
    return res;
}

int main() {
    ios::sync_with_stdio(false);
    cin.tie(0);
    
    init_trie();
    int n;
    cin >> n;
    vector<int> a(n);
    for (int i = 0; i < n; i++) {
        cin >> a[i];
        insert(a[i]);  // 插入所有数到Trie树
    }
    
    int max_xor = 0;
    for (int x : a) {
        // 对每个数，找异或最大的数，更新最大值
        max_xor = max(max_xor, find_max_xor(x));
    }
    
    cout << max_xor << endl;
    return 0;
}

测试用例：

输入：

3
1 2 3

输出：

3

解释：3（11）和 1（01）异或结果是 2（10），3 和 2（10）异或结果是 1（01），2 和 1 异或结果是 3（11），最大值为 3。

五、避坑指南：Trie 树常见问题与优化

在实际使用 Trie 树时，很容易因为细节问题导致超时或错误。这里总结几个高频坑点和优化方案：

5.1 坑点 1：数组大小不够导致越界

Trie 树的节点数 = 所有字符串的长度之和。比如 n=1e4 个字符串，每个长度 100，节点数就是 1e6，所以数组大小要设为 1e6+10，避免越界。

优化方案：

• 估算节点数：如果题目中字符串总长度不超过 1e6，数组大小设为 1e6+10；如果总长度不超过 3e6，设为 3e6+10。
• 多组测试数据时，用循环清空节点（如for (int i=0; i<=idx; i++) memset(tr[i], 0, sizeof tr[i])），避免memset整个大数组（效率低）。

5.2 坑点 2：输入输出未加速导致超时

当字符串数量或长度较大时（如 n=1e5、字符串长度 = 1e3），cin和cout的默认速度会很慢，导致超时。

优化方案 ：在main函数开头加入：

ios::sync_with_stdio(false);
cin.tie(0);

这两句代码会关闭cin与stdio的同步，加速输入输出（注意：之后不能混用cin和printf）。

5.3 坑点 3：字符处理错误（大小写、特殊字符）

比如题目要求处理大写字母，但代码只处理了小写字母，导致路径编号错误，查询结果为 0。

优化方案：

• 明确题目是否大小写敏感：如果不敏感，先将字符串统一转为小写或大写（如transform(s.begin(), s.end(), s.begin(), ::tolower)）。
• 用get_num函数统一处理字符转路径，避免手动计算错误。

5.4 坑点 4：多组测试数据未初始化

如果多组测试数据共用一个 Trie 树，上一组数据的节点会残留，导致当前组结果错误。

优化方案：

• 每组测试数据开始前，调用init_trie函数清空 Trie 树（重置tr、p、e数组和idx）。
• 清空时优先用循环清空（效率高），避免memset大数组。

5.5 优化：空间优化（压缩节点）

传统 Trie 树用二维数组存储子节点指针，空间利用率不高。可以用 "动态数组" 或 "结构体 + 指针" 的方式，动态创建节点，节省空间。

动态节点实现示例：

struct TrieNode {
    TrieNode* children[26];  // 子节点指针
    int p;                   // 前缀计数
    int e;                   // 单词计数
    TrieNode() {
        memset(children, 0, sizeof children);
        p = 0;
        e = 0;
    }
};

TrieNode* root = new TrieNode();  // 根节点

// 插入字符串
void insert(string& s) {
    TrieNode* cur = root;
    cur->p++;
    for (char ch : s) {
        int path = ch - 'a';
        if (!cur->children[path]) {
            cur->children[path] = new TrieNode();  // 动态创建节点
        }
        cur = cur->children[path];
        cur->p++;
    }
    cur->e++;
}

注意：动态节点需要手动释放内存（避免内存泄漏），适合空间紧张的场景，普通题目用静态数组更简单。

---

总结

Trie 树是数据结构中的 "小而美" 的算法，掌握它能让你在处理字符串问题时事半功倍。希望这篇文章能帮助你彻底搞懂 Trie 树，在算法路上更进一步！

如果觉得文章对你有帮助，欢迎点赞、收藏、转发，也可以在评论区交流你的学习心得和遇到的问题～