有向距离场(Signed Distance Field,SDF)作为一种强大的数学表示方法,已成为现代实时图形引擎的核心技术之一。它通过将离散的几何信息表示为连续的标量场,为全局光照、软阴影、环境光遮蔽等多种图形效果提供了统一而高效的几何基础。
1. SDF的数学基础与核心优势
有向距离场本质上是定义在3D空间中的标量场,它为空间中的任意一点 p赋予一个距离值,表示该点到最近物体表面的有符号距离:点在物体外部时为正,内部为负,表面为零。这一简单的定义带来了诸多关键优势:
SDF的平滑插值特性使其能够提供高质量的几何表示。在两个体素之间,距离值可以平滑过渡,这使得从SDF重建的曲面非常光滑,没有多边形感。与传统的三角形网格表示相比,SDF对几何复杂度的敏感度更低,一个相对低分辨率的SDF就能表示相当复杂的几何形状。
SDF支持高效的几何查询和操作。给定空间中的任意一点,可以快速计算出它到最近表面的距离,以及该表面的法线方向(通过计算梯度)。更重要的是,SDF通过布尔运算(并集、交集、差集)和平滑混合操作,可以无缝地组合多个形状,这完全不同于传统的多边形网格布尔运算(后者通常容易出错且拓扑复杂)。
SDF的分辨率无关性使其特别适合高质量渲染。如同距离场字体在任何分辨率下都能呈现完美光滑的边缘,将这一思路扩展到整个几何渲染,可以实现超越传统抗锯齿技术的高质量渲染效果。
2. SDF的高效计算与GPU并行架构
在GPU上高效计算SDF值是实现实时渲染的关键。现代图形引擎采用多种策略来加速SDF的构建和更新。
2.1 场景划分与体素化
SDF计算首先需要将场景划分为三维体素网格。每个体素存储对应空间位置的SDF值,体素大小直接影响计算精度和内存消耗。对于复杂场景,通常采用稀疏化存储策略,只分配内存给那些真正需要表示物体表面的体素块,从而大幅降低内存需求。
2.2 跳跃泛洪算法(JFA)优化
对于动态场景,传统的暴力SDF计算方法效率低下。跳跃泛洪算法(Jump Flooding Algorithm,JFA)通过多轮迭代逐步传播距离信息,将计算复杂度从O(N×M)降低到O(NlogL),其中N是像素数,M是种子点数,L是图像边长。
JFA的核心思想是通过一系列步长递减的迭代,让每个像素在每一步中查询周围特定偏移位置的种子信息,更新为最近的种子点。这种算法特别适合GPU并行架构,能够高效生成动态SDF。尽管JFA是一个近似算法,在某些情况下可能会产生微小的误差,但对于游戏应用来说,其极高的性能和几乎可以忽略不计的视觉误差是完全可以接受的。
JFA算法核心原理
跳跃泛洪算法是一种用于在GPU上高效计算离散Voronoi图或距离变换的并行算法。其核心思想是通过一系列步长递减的跳跃步骤来传播种子点的信息,而非传统的逐像素传播。
-
算法流程
JFA的执行过程如下面的流程图所示,它通过多轮步长递减的迭代,快速而高效地传播距离信息。
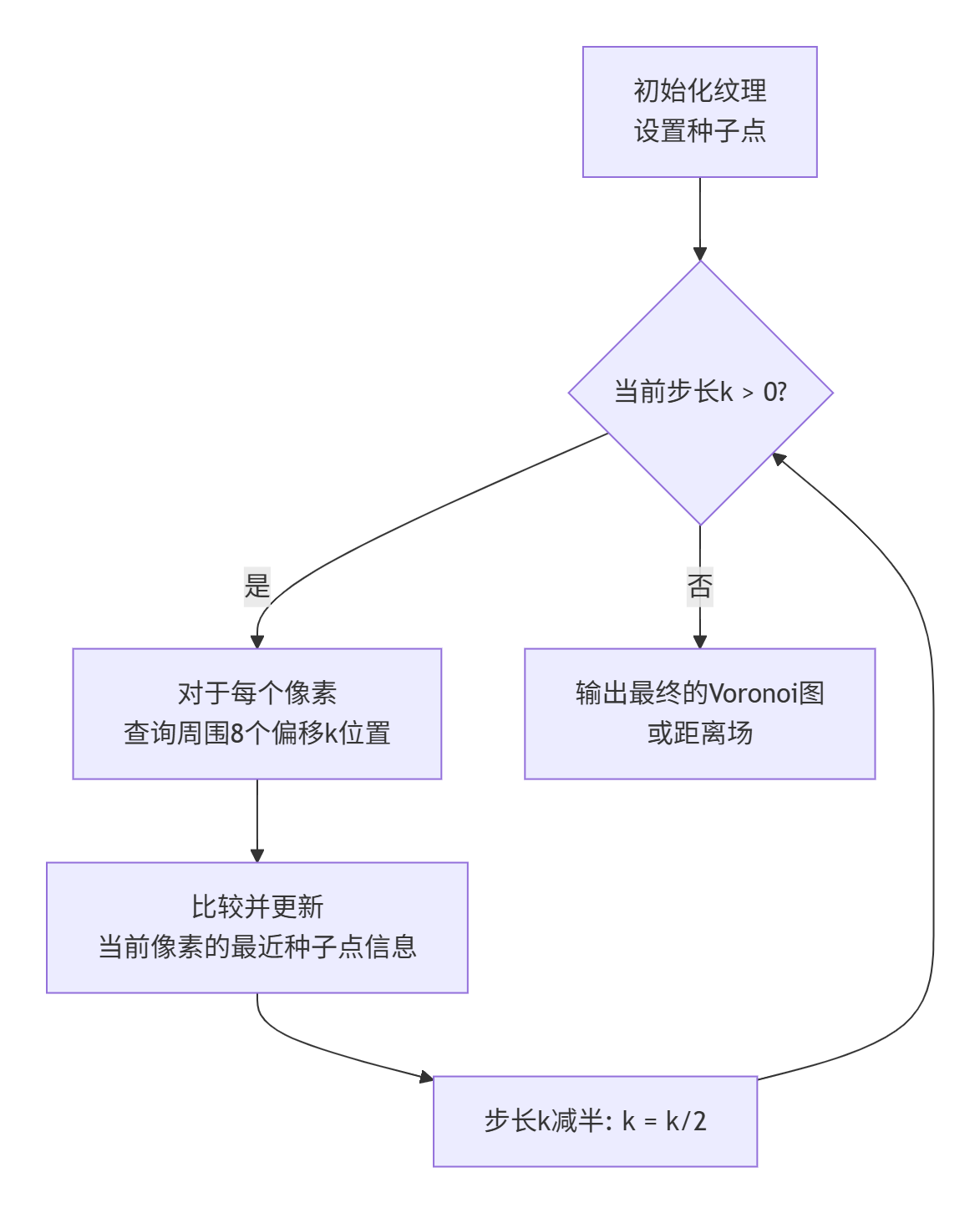
-
初始化:创建一个与输出图像分辨率相同的纹理,将所有像素初始化为一个"未定义"状态。然后将种子点(例如,Voronoi图的站点,或SDF中的表面点)的位置和ID写入对应的像素。
-
迭代泛洪 :算法进行一个固定次数的循环迭代,每次迭代的"跳跃步长"
k都会减半,通常从N/2开始(N为图像边长),依次为N/2, N/4, ..., 1。 -
并行更新 :在每次迭代中,每个像素(一个GPU线程)会检查其周围8个(或包括自身的9个)特定偏移位置上的像素。偏移量由当前的步长
k决定,例如偏移坐标为(±k, ±k),(0, ±k),(±k, 0)。线程会比较从这些位置采样到的种子点信息,如果发现某个采样点所代表的种子点距离当前像素更近,则用该种子点信息更新当前像素。
JFA的实现细节
以下以在图形API(如OpenGL/ Vulkan)中实现JFA生成距离场为例。
-
资源准备
-
纹理与缓冲区 :需要创建多个纹理或缓冲区用于数据交换。通常采用"乒乓渲染"策略,使用两个纹理交替作为输入和输出,以避免数据竞争。纹理格式应支持存储向量数据(如
RGBA32F),以便同时保存最近种子点的ID和距离信息。 -
着色器程序:实现通常涉及多个着色器程序或计算着色器内核(Kernel):
-
初始化着色器:负责将种子点数据写入纹理。
-
泛洪着色器:这是JFA的核心,执行上述的迭代更新逻辑。
-
后处理/显示着色器:用于可视化结果或进行最终处理。
-
-
2.3 多分辨率与层次化结构
大规模场景的SDF表示面临内存消耗的挑战。现代图形引擎采用多级细节 (LOD)策略:根据视距使用不同精度的SDF,近处高精度、远处低精度。如UE5的Lumen系统使用网格距离场 (Mesh SDF)表示单个物体的高精度几何,而全局距离场(Global Distance Field,GDF)则表示整个场景的低精度SDF。
这种混合方案确保了"好钢用在刀刃上",在保证近处细节的同时,不让远处的细节拖垮性能。对于动态物体,系统会检测发生变化的空间区域,并只更新这些区域的SDF值,避免全局更新的开销。
3. SDF在实时渲染中的高级应用
3.1 全局光照与软阴影
UE5的Lumen系统核心就依赖于Mesh Distance Fields(网格距离场)。它用低分辨率的SDF来表示场景的全局几何,用于高效的有向距离场光线行进(SDF Raymarching),来计算漫反射和镜面反射的间接光照。
在软阴影计算中,通过查询SDF,光线在朝向光源行进时,可以累积"遮蔽"信息,从而生成非常自然、柔和的区域阴影(Area Shadows),其质量远高于传统的Shadow Maps。SDF查询可以快速确定着色点与光源之间的可见性关系,通过考虑光源区域内的遮挡情况,产生物理准确的软阴影效果。
3.2 动态漫反射全局光照(DDGI)
DDGI技术结合了SDF与光照探针,实现了高效的动态全局光照。其核心原理是对每个需要参与全局光照的物体生成SDF离线数据,运行时将所有的SDF数据组合生成场景级的GDF(Global Distance Field)。
在光线追踪过程中,对近处的物体使用精度更高的Mesh SDF进行求交处理,对于较远的物体则采用GDF求交。这种分层次的求交策略在保证质量的同时大幅提高了性能。当光线与表面相交时,会生成一个Surfel,表示所击中物体表面上的一个点,并携带该点的位置、法线以及表面颜色等数据,用于后续的光照计算。
3.3 可微分SDF渲染
Siggraph 2022的开源项目"Differentiable Signed Distance Function Rendering"将SDF与可微分渲染相结合,实现了通过神经网络直接优化3D形状的能力。这种技术将3D物体表示为有符号距离场并实现可微分渲染,为逆向图形学、机器人视觉、AR/VR内容创作等场景提供了强大的3D处理能力。
可微分SDF渲染的核心优势在于端到端可微,无缝衔接深度学习。通过PyTorch框架实现的自动微分功能,可以直接优化3D模型参数,无需手动推导梯度公式。这为基于图像的3D重建、材料估计等任务提供了强大的工具。
Siggraph 2022的开源项目"Differentiable Signed Distance Function Rendering"实现了端到端可微的SDF渲染管线,将传统的图形学渲染流程与深度学习框架无缝衔接。该项目的主要创新在于解决了SDF表示在可微分渲染中的关键挑战,为3D重建、逆向图形学、机器人视觉等应用提供了强大的基础工具。
项目的核心价值体现在:
-
端到端可微:支持从2D观测(图像)直接优化3D几何(SDF参数)
-
物理精度:基于真实的体渲染方程,而非神经渲染的黑盒近似
-
计算效率:充分利用GPU并行性和现代深度学习框架的自动微分能力
2. 技术原理深度解析
2.1 可微渲染的基础数学框架
可微SDF渲染建立在体渲染积分的数学基础上。与传统表面渲染不同,该方法将场景视为参与性介质,通过累积光线上的光学贡献来计算最终像素颜色。
体渲染方程可表示为:
C(r) = ∫[t_n, t_f] T(t) * σ(r(t)) * c(r(t), d) * dt
其中:
-
C(r)是光线r的最终颜色 -
T(t) = exp(-∫[t_n, t] σ(r(s)) ds)是透射率(累积透明度) -
σ(x)是密度函数(与SDF相关) -
c(x, d)是辐射函数(颜色+视角依赖)
2.2 SDF到密度场的可微转换
项目的关键技术突破在于实现了从SDF到密度场的可微转换。传统方法使用硬表面假设(SDF=0处为表面),但这会导致梯度消失问题。
4. 技术挑战与优化策略
尽管SDF技术具有诸多优势,但在实际应用中仍面临多项挑战。
4.1 内存与存储优化
高分辨率SDF会消耗巨量内存。优化策略包括高效压缩算法 开发、稀疏化存储 (只存储物体表面附近的关键体素数据)以及动态流送 (根据需要动态加载和卸载SDF数据)。体素哈希(Voxel Hashing)技术使用哈希表管理内存,键是体素块在世界空间中的整数坐标,值是指向该体素块实际存储的SDF数据的指针,能极大节省内存。
4.2 生成与更新速度
为复杂场景生成SDF是计算密集型任务。优化策略包括硬件加速 (利用Compute Shader在GPU上并行生成)和增量更新(只更新发生变化区域的SDF,而不是全场景重新生成)。对于动态场景,还可以为每个动态物体维护独立的SDF,随着物体一起移动和旋转,在需要时查询世界静态场景的SDF和所有相关动态物体的SDF,取最小值。
4.3 精度与误差控制
低分辨率SDF会带来几何细节丢失。解决方案包括结合传统网格 (在极近处使用传统高模,在中远处使用SDF)和自适应SDF (在曲率高的细节区域自动使用更高分辨率的SDF)。此外,多级SDF(HLOD for SDF)层次结构在远处使用低分辨率SDF进行快速查询,在近处使用高分辨率SDF获取细节,实现性能与质量的平衡。
5. 未来展望:SDF-First渲染架构
基于SDF的优化,其核心思想是将几何信息从离散的多边形表示,转化为连续的、富含信息的数学场表示。对于未来的图形引擎,我们可能会看到一个"SDF-First"的渲染架构。
在这一架构中,SDF将作为核心数据源:场景的权威几何表示是一个统一的、层次化的SDF。渲染管线围绕SDF构建:全局光照、阴影、环境光遮蔽、抗锯齿乃至几何变形都直接查询这个统一的SDF数据源。