参考视频
https://www.bilibili.com/video/BV12HE8zsEnb/?spm_id_from=333.337.search-card.all.click&vd_source=132c74f7a893f6ef64b723d9600c40b7PCA：principal component analysis
PCA是一种将为方式
特征在不同维度上的分布差异不同
通过将原始的高维度特征投影到方差分布最大的方向上来降低维度。并保持数据间的差异性
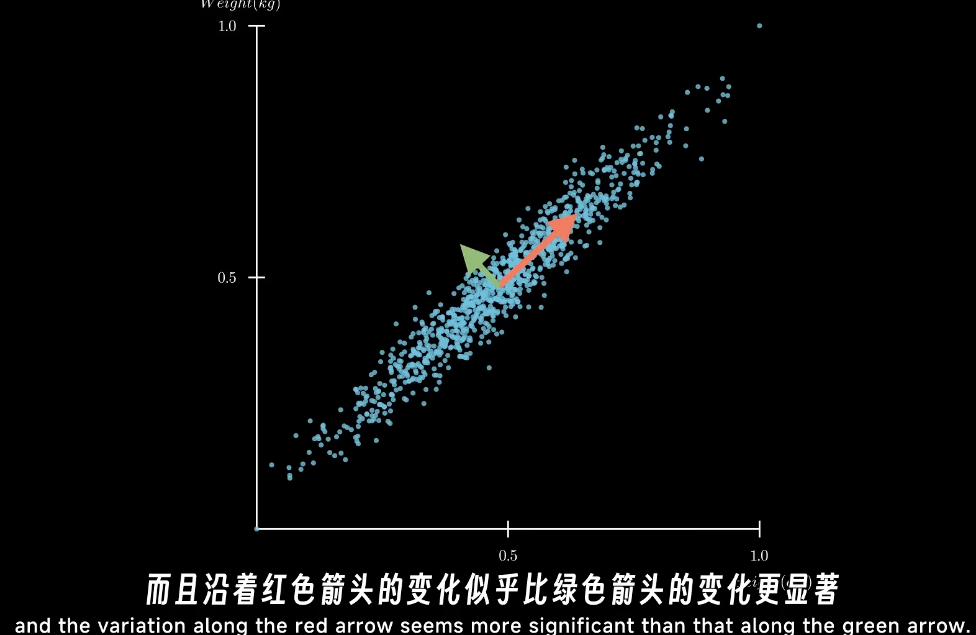
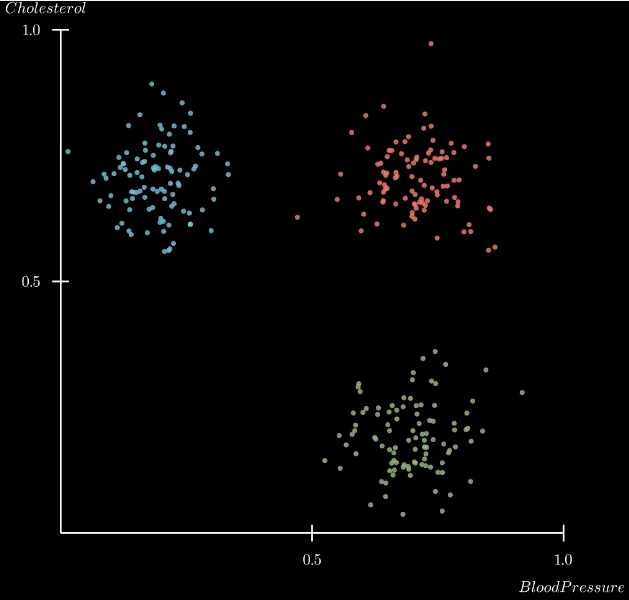
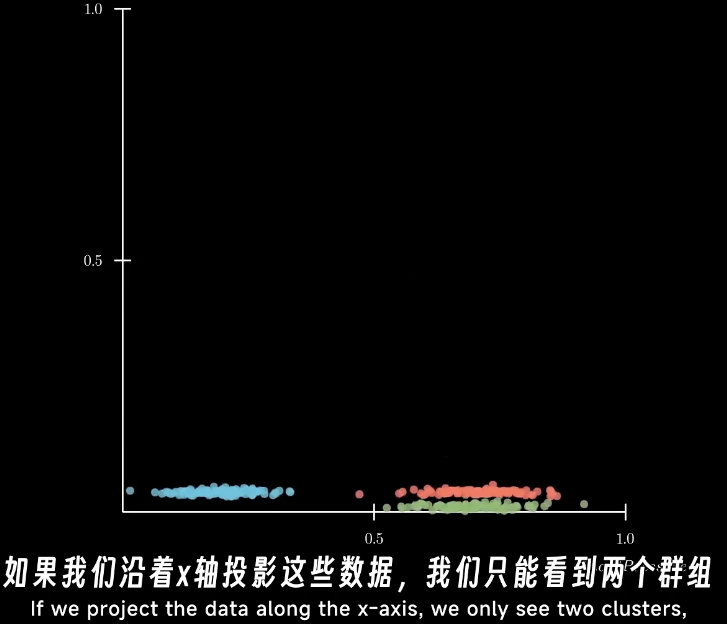
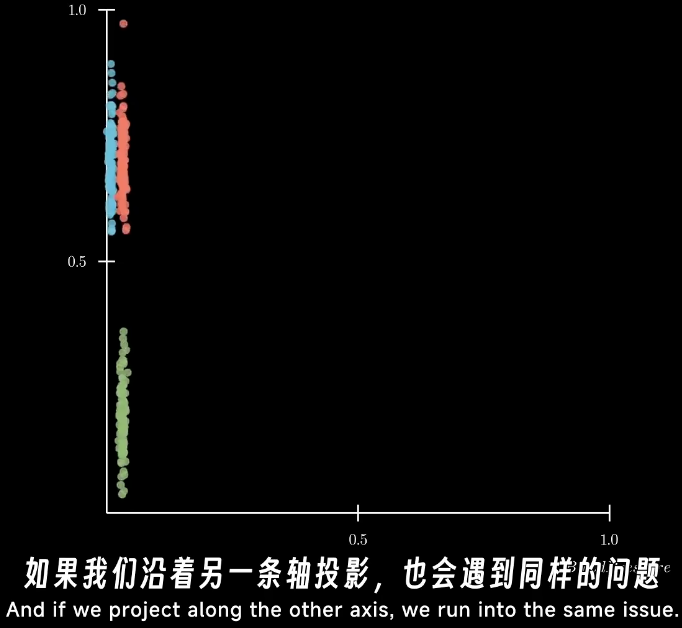
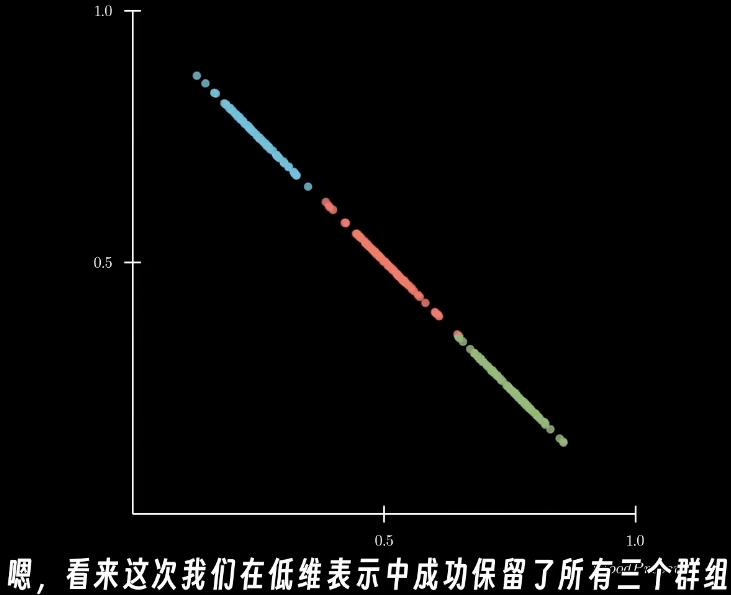
而投影到主成分上时，低维的数据还是保持了高维度的可区分性
计算方式：
1，首先对数据进行中心化，数据减去均值
2，计算协方差矩阵
3，找到协方差矩阵的特征向量
4，根据特征值将这些特征向量降序排列
5，特征值最大的特征向量即为主成分
6，构造出一个矩阵，将原始的数据投影到主成分的轴上
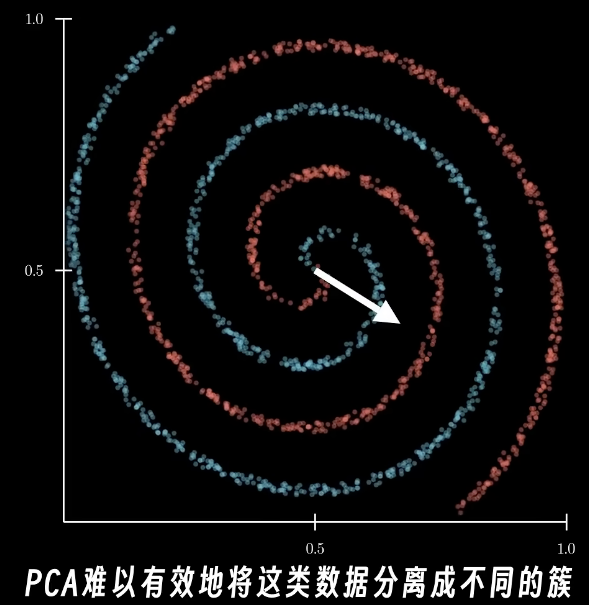
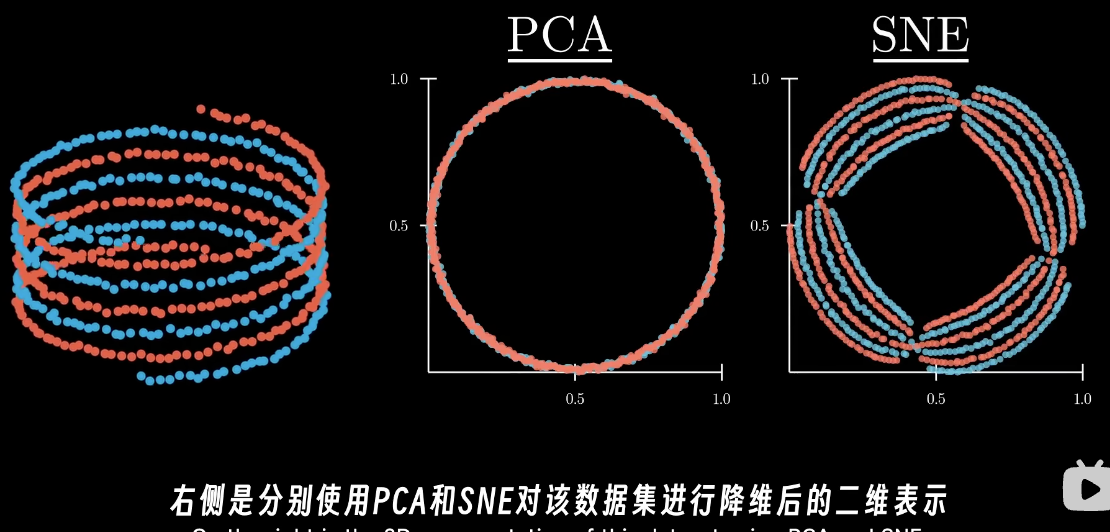
PCA是线性的，因此在非线性的数据分布上得到的结果不好
SNE和t-SNE： t- distributed stochastic neighbor embedding
t-SNE在2008年由hintion开发，基于他之前在2002年的工作SNE
SNE
SNE的思想：在高维度中的数据之间的距离，在低维度的表示中也应该保持相似
SNE可以处理非线性的数据分布
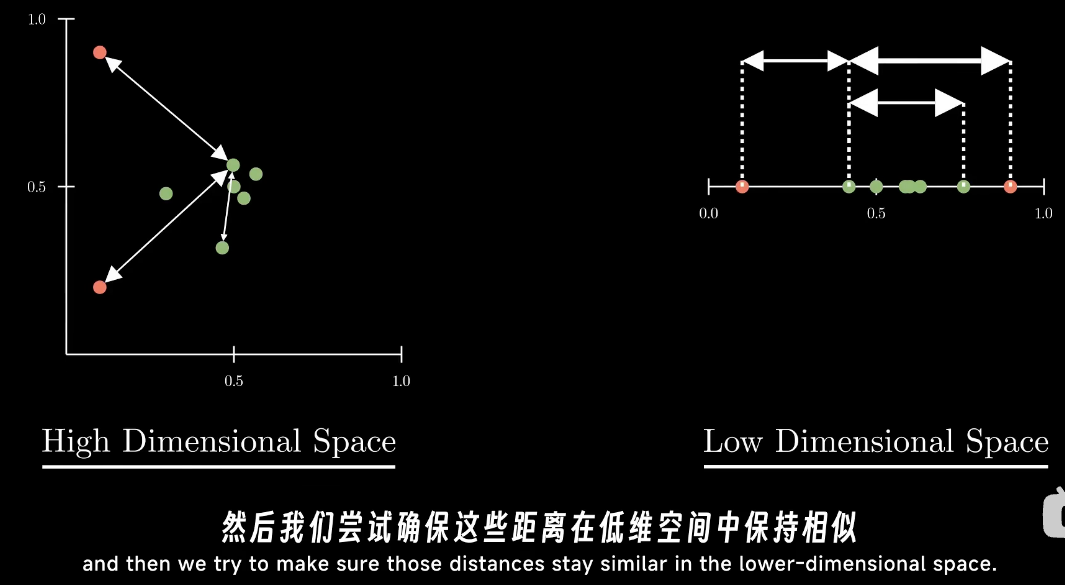
SNE思想：
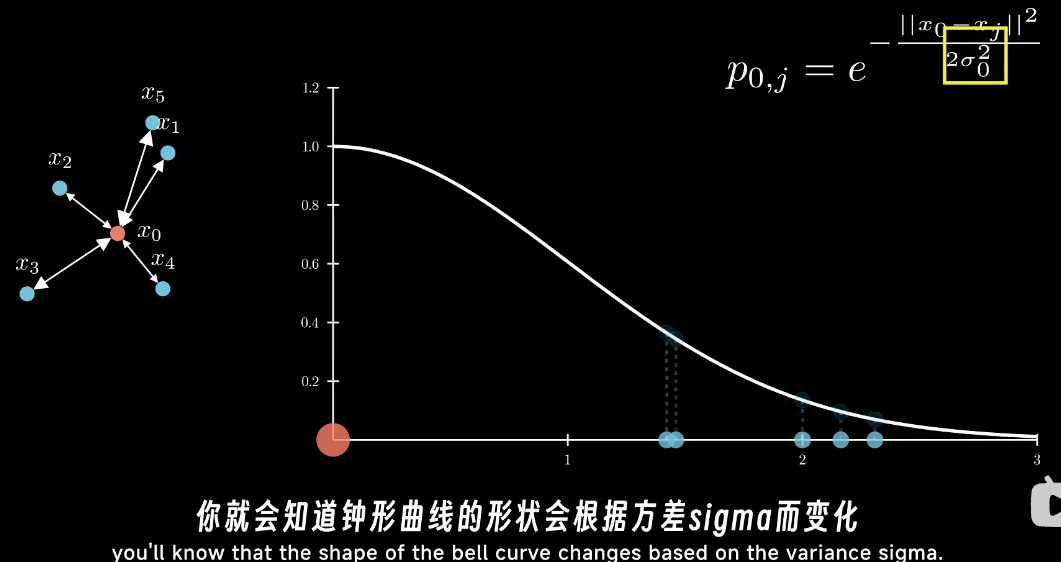
对于一个参考点，用高斯分布的概率值来表示他周围的点是这个参考点的领居的概率
其中距离就是二范数距离
而这个高斯的sigma的取值，用困惑度（perplexity）来表述
对每个点，都按照上述方式计算邻居概率。最后再归一化到0
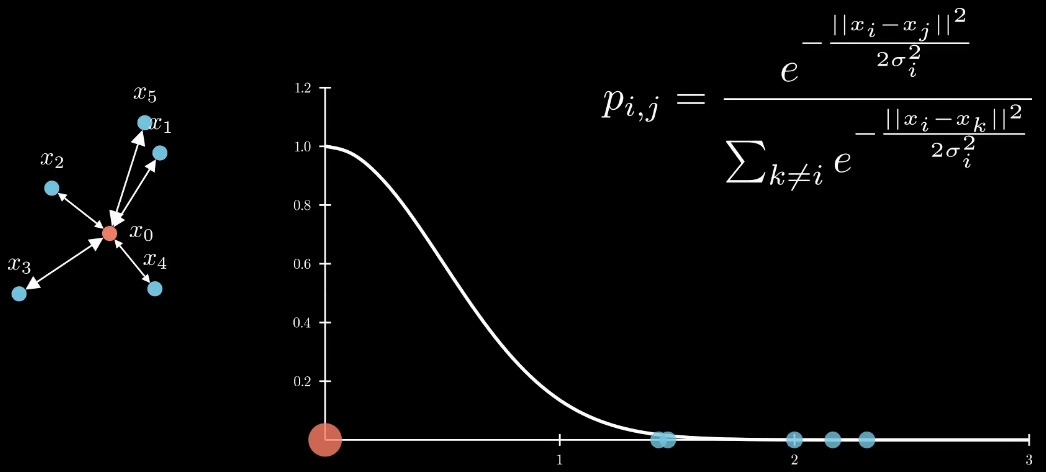
另外，在另一个低维空间中，也随机化同样个数的初始点，然后用同样的公式计算这个概率
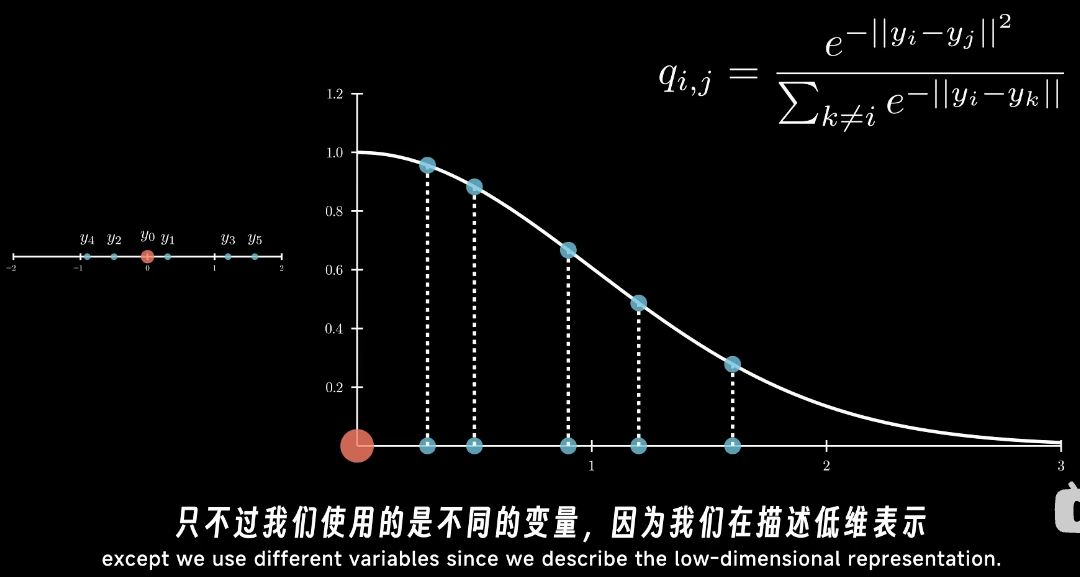
最终优化的目标就是让这两个分布尽量接近
通过KL散度的方式来计算这两个分布之间的距离
根据这个公式进行求导即可优化
t-SNE
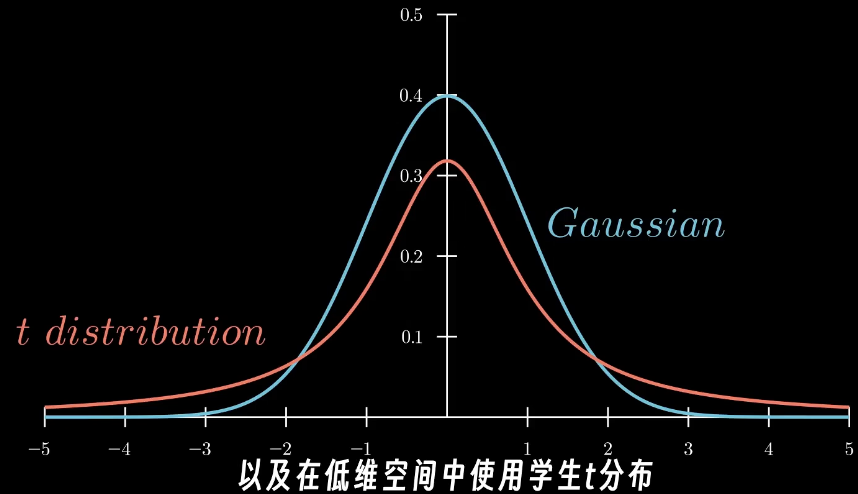
SNE的缺点就是计算的速度非常慢
因此t-SNE调整了分布，在低维空间中使用t分布
但是，t-SNE的效果仍然非常收到perplexity的影响，不同的perplexity得到的结果可能相差很大
UMAP：Uniform Manifold Approximation and Projection
UMAP这个方法是2018年被提出的
UMAP的思想和SNE其实差不多，区别就是将高斯概率的表示方法换成了用图来表示
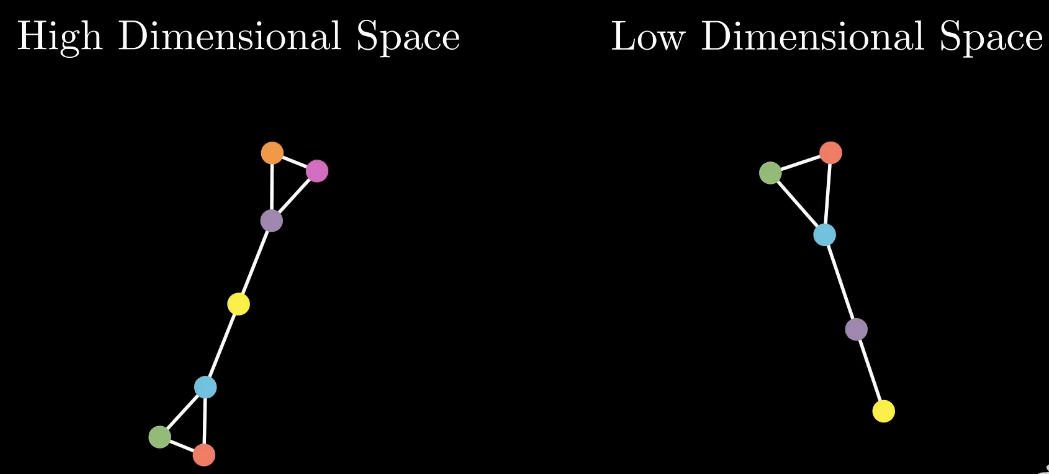
通过找每个参考的k个最近邻的邻居点，因此就得到了一个二维的图
得到最近的几个点之后，通过下面的公式来计算距离权重（类似SNE），rou参数的目的是让最近的点的权重为1
对每个参考点都进行上述的运算
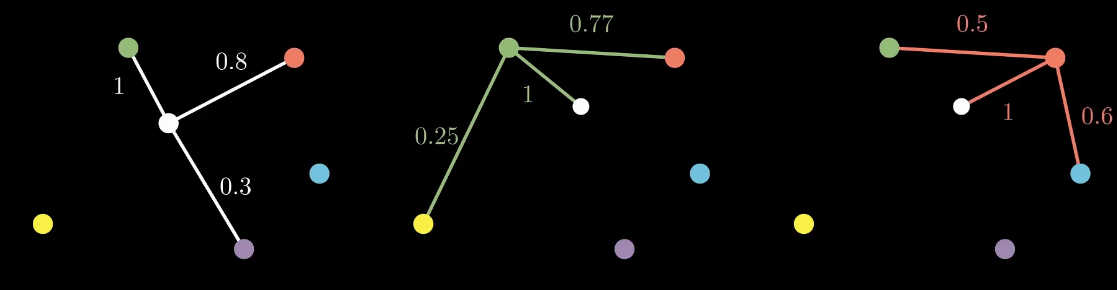
然后将这些子图合成到一个图里面，将两条边和成一条边
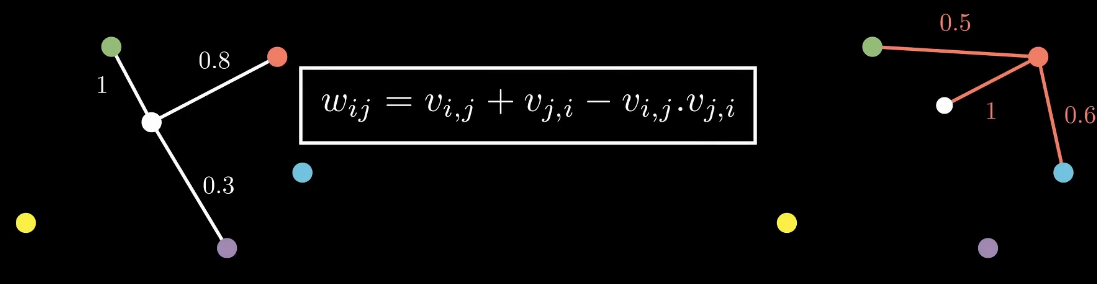
最后通过优化高维空间和低维空间的加权图矩阵的距离来实现低维表示
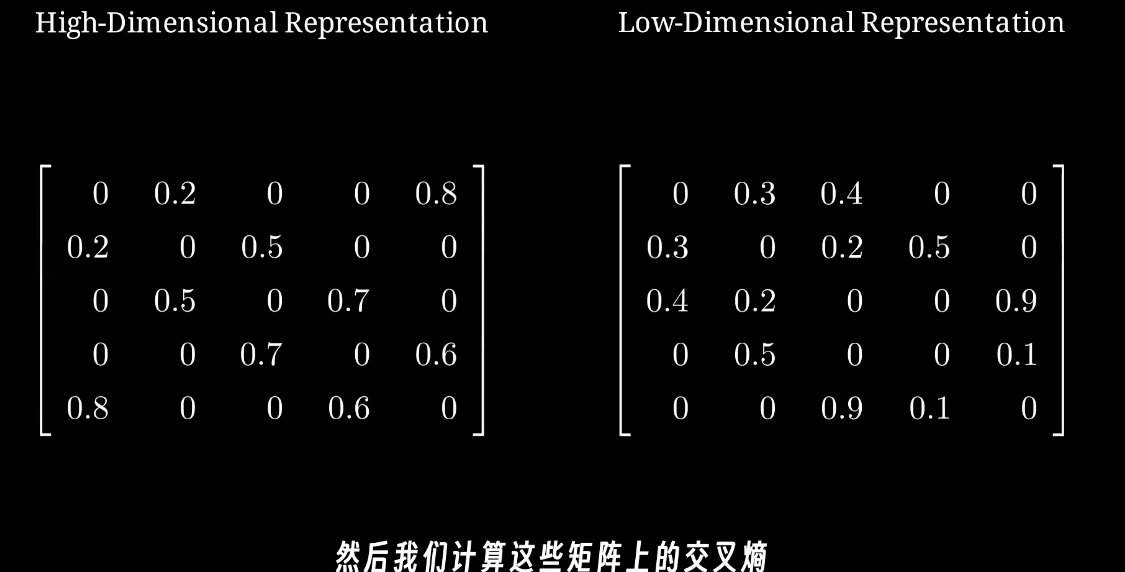
用随机梯度下降和交叉熵来优化这两个矩阵之间的距离
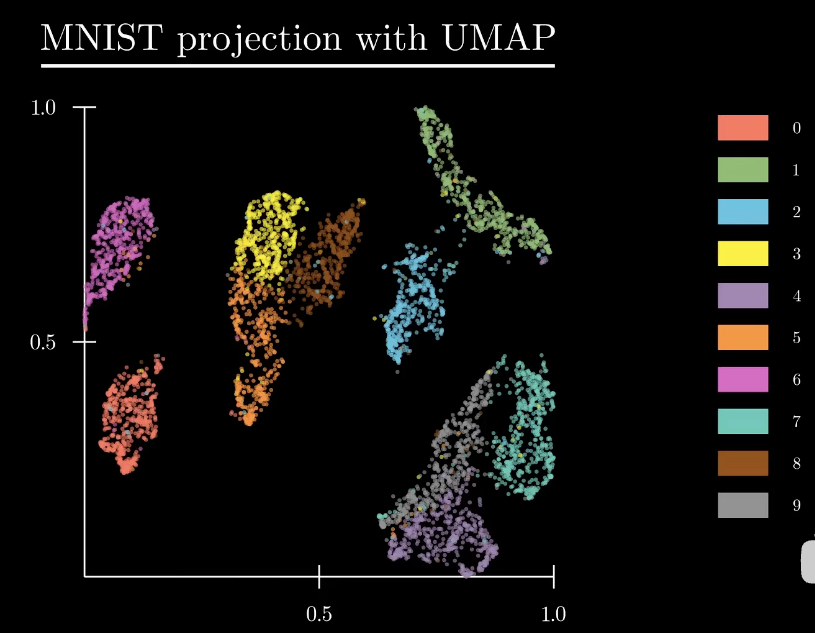
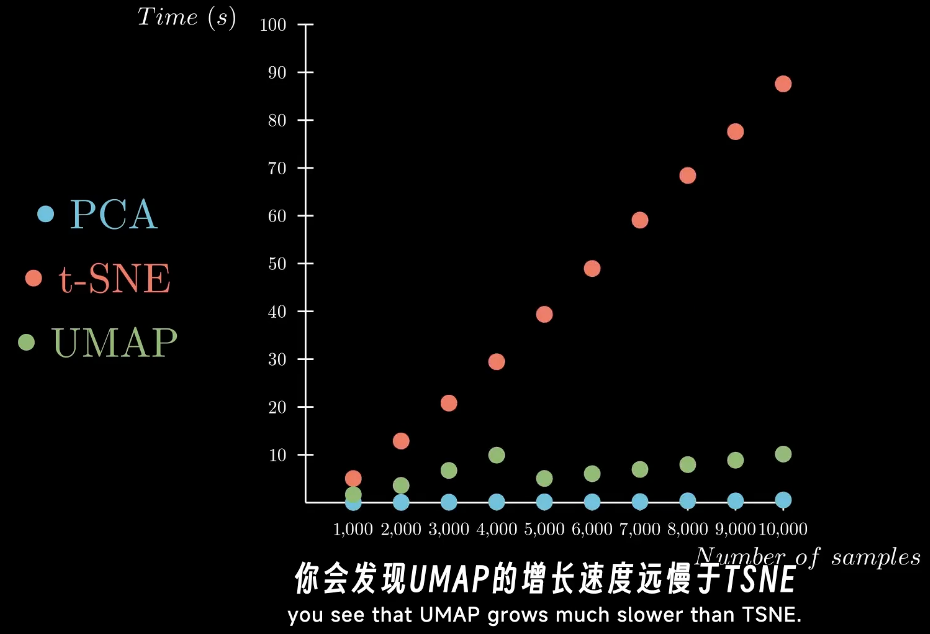
UMAP的速度比t-SNE快得多，并且效果更好，而且可以更好的保留全局的结构