算法深潜：链表中的生死之环（LeetCode 141 & 142 详解）

🏠 个人主页: EXtreme35

📚 个人专栏:

专栏名称	专栏主题简述
《C语言》	C语言基础、语法解析与实战应用
《数据结构》	线性表、树、图等核心数据结构详解
《题解思维》	算法思路、解题技巧与高效编程实践

第一部分：判断链表是否有环
- [1. 问题描述](#1. 问题描述)
- [2. 核心思路：快慢指针法](#2. 核心思路：快慢指针法)
- [3. 数学证明（重点）](#3. 数学证明（重点）)
- - [Q1: 为什么快指针走2步，慢指针走1步，两者一定会相遇？](#Q1: 为什么快指针走2步，慢指针走1步，两者一定会相遇？)
  - [Q2: 如果不按照当前设定走呢？还能保证相遇吗？](#Q2: 如果不按照当前设定走呢？还能保证相遇吗？)
第二部分：寻找环的入口
- [1. 问题描述](#1. 问题描述)
- [2. 核心思路：双指针二次相遇](#2. 核心思路：双指针二次相遇)
- [3. 数学推导（图解逻辑）](#3. 数学推导（图解逻辑）)
第三部分：复杂度

在链表数据结构中，"环"是一个经典且考察频率极高的话题。这类问题通常分为两个阶段：

判断是否有环 （LeetCode 141. 环形链表）。
如果有环，找出环的入口 （LeetCode 142. 环形链表 II）。

第一部分：判断链表是否有环

1. 问题描述

给你一个链表的头节点 head ，判断链表中是否有环。

如果链表中有某个节点，可以通过连续跟踪 next 指针再次到达，则链表中存在环。为了表示给定链表中的环，评测系统内部使用整数 pos 来表示链表尾连接到链表中的位置（索引从 0 开始）。注意：pos 不作为参数进行传递 。仅仅是为了标识链表的实际情况。

如果链表中存在环，则返回 true 。否则，返回 false 。

2. 核心思路：快慢指针法

我们定义两个指针：

慢指针 (slow)：一次走 1 步。
快指针 (fast)：一次走 2 步。

算法流程：

初始化 slow 和 fast 都指向头节点 head。
只要 fast 和 fast->next 不为空，循环执行：
- slow 前进 1 步。
- fast 前进 2 步。
- 如果 fast == slow，说明相遇，链表存在环。
如果循环结束（fast 遇到 NULL），说明无环。

代码实现 (C语言)

c 复制代码

/**
 * Definition for singly-linked list.
 * struct ListNode {
 * int val;
 * struct ListNode *next;
 * };
 */
bool hasCycle(struct ListNode *head) 
{
    if (head == NULL || head->next == NULL) 
        return false;
    //快慢指针
    struct ListNode *slow = head;
    struct ListNode *fast = head;
    while (fast != NULL && fast->next != NULL) 
    {
        slow = slow->next;      // 慢走1步
        fast = fast->next->next; // 快走2步
        if (slow == fast)
            return true; // 相遇，有环
    }
    return false; // 走到尽头，无环
}

3. 数学证明（重点）

Q1: 为什么快指针走2步，慢指针走1步，两者一定会相遇？

证明（相对速度法）：

我们假设在慢指针刚刚进入环 的那一时刻，快指针开始追，这时候不知道快指针已经走多少圈了，就假设在此时我图中标记的位置。

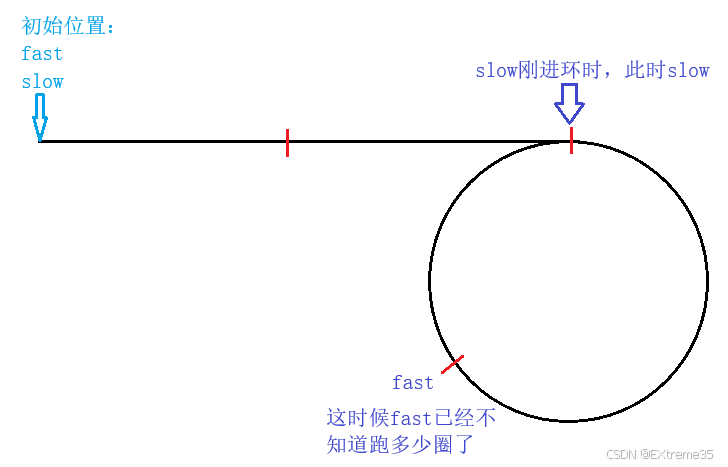
下来我们为了证明是否一定能追上，定义几个距离，看看最后是否能推出一个数学表达式。

假设从初始位置到刚进入环的距离是L。
假设 slow 进入环时，fast 追上 slow 的距离为 N N N（沿链表运行方向）。
假设链表环长度为C。

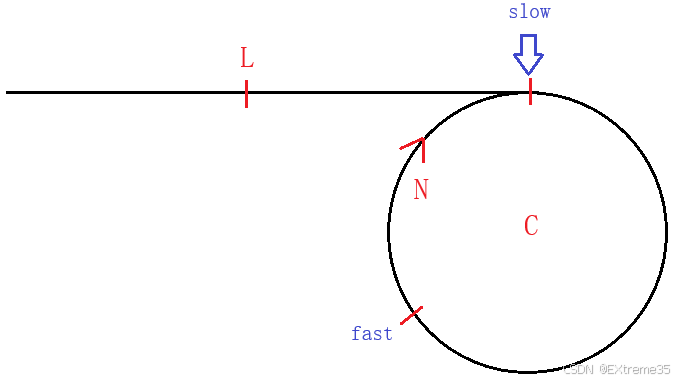
现在fast速度是slow的两倍，也就是每次多走1 ，也就是在N这个距离中，每次距离会少1 ，直至为0，一定会追上。
N → N − 1 → N − 2 → . . . → 1 → 0 N \rightarrow N-1 \rightarrow N-2 \rightarrow ... \rightarrow 1 \rightarrow 0 N→N−1→N−2→...→1→0
证明总结：

当 slow 进入环之后，fast 已经在环内了。
假设 slow 进入环时，fast 领先 slow 的距离为 N N N（沿链表运行方向）。
我们将 slow 看作静止，那么 fast 相对于 slow 的移动速度是 2 − 1 = 1 2 - 1 = 1 2−1=1 步/次。
每一次迭代，fast 都会把它和 slow 之间的距离缩短 1。
距离变化过程： N , N − 1 , N − 2 , . . . , 1 , 0 N, N-1, N-2, ..., 1, 0 N,N−1,N−2,...,1,0。

结论：因为距离每次减 1，必然会减到 0（相遇），绝对不会跳过去。

Q2: 如果不按照当前设定走呢？还能保证相遇吗？

这是一个非常好的进阶面试题。

分析：

在刚才的分析中，我们是找到了相对速度，每次会少一步。
- 如果快指针走 3 步，慢指针走 1 步，相对速度 是 3 − 1 = 2 3 - 1 = 2 3−1=2。
- 如果快指针走 4 步，慢指针走 1 步，相对速度 是 4 − 1 = 3 4 - 1 = 3 4−1=3。
这意味着 fast 每次把距离缩短一个相对速度的距离。
还是按照上面的假设进行推演，得到每次相距的距离。

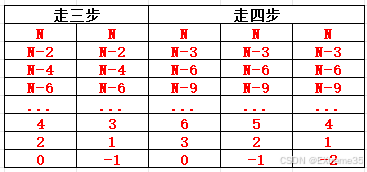
这里为什么有这么多情况呢？因为不知道N到底有多大，它有可能是奇数、偶数、0，都有可能。

所以需要对每一个结果进行讨论，当最后距离为0的时候，显然已经追上了，那么-1代表什么意思呢？很显然，代表这时候已经进入下一轮追击了，且快指针就在慢指针前面一个位置。那个-2也是一样的道理。

那我们之前设的圆环长度还一直没用呢，这时候就派上用场了。-1、-2，那这时候相对距离就是C-1、C-2。

走三步的情况下：

N为偶数，第一轮追上。
N为奇数，第一轮错过，看环长度。
- C − 1 C-1 C−1 为奇数，那么永远追不上。
- C − 1 C-1 C−1为偶数，那么下一轮就追上了。

走四步的情况：

走四步就不能看奇偶了，而是是不是三的倍数，因为每次距离会少三，所以三的倍数一定会追上。

N % 3 = 0，首轮就追上。
N % 3 = 1，首轮错过，看环长。
- (C-1) % 3 = 0 ，下一轮追上。
- (C-1) % 3 = 1 ，永远追不上。
- (C-1) % 3 = 2 ，看下述情况。
N % 3 = 2 `，首轮错过，看环长。
- (C-1) % 3 = 0 ，下一轮追上。
- (C-1) % 3 = 1 ，看上述情况。
- (C-1) % 3 = 2 ，永远追不上。

那么有没有一个稍微通用的结论呢？尝试一下

设慢指针 slow 进环时，快指针 fast 与 slow 的距离为 N
设 slow 进环前走的距离为：L
fast 在 slow 进环前已经绕环转了 x 圈

距离关系分析

fast 走的总距离为：L + x*C + (C - N)。
slow 走的距离为： L。

这时候就算是有个半成品的等式了，现在只需要带入速度关系就可，以3倍为例：

3L = L + (x+1)*C - N
化简后：2L = (x+1)*C - N，这时候就可以用奇偶关系判断了。

关键分析： 如果同时存在以下两个条件：N 是奇数 、C 是偶数。

那么根据公式： 偶数 = (x+1)*偶数 - 奇数

逻辑矛盾推导

(x+1)*偶数 的结果一定是偶数
只有 奇数 - 奇数 = 偶数 才成立
但等式中是 偶数 - 奇数，这在整数范围内不可能成立，故一定追不上。

结论： 如果步同时存在 N 是奇数 且 C 是偶数 的情况，永远追不上的条件不成立，因此快慢指针一定能相遇。

相遇情况总结

当 N 是偶数：第一轮追击就能相遇
当 N 是奇数 、C 是偶数，一定追不上。
其他情况都会在后面几轮追上。

第二部分：寻找环的入口

1. 问题描述

给定一个链表的头节点 head ，返回链表开始入环的第一个节点。如果链表无环，则返回 null。

如果链表中有某个节点，可以通过连续跟踪 next 指针再次到达，则链表中存在环。为了表示给定链表中的环，评测系统内部使用整数 pos 来表示链表尾连接到链表中的位置（索引从 0 开始 ）。如果 pos 是 -1，则在该链表中没有环。注意：pos 不作为参数进行传递 ，仅仅是为了标识链表的实际情况。
不允许修改链表。

2. 核心思路：双指针二次相遇

第一次相遇：使用快慢指针判断是否有环，若有环，记录相遇点。
寻找入口 ：
- 让一个指针从 头节点 (Head) 出发。
- 让另一个指针从 相遇点 (Meeting Node) 出发。
- 两个指针都每次走 1 步。
- 它们最终会在 环入口 (Entry Node) 相遇。

代码实现 (C语言)

c 复制代码

struct ListNode *detectCycle(struct ListNode *head) 
{
    struct ListNode *slow = head;
    struct ListNode *fast = head;
    
    // 步骤一：判断是否有环
    while (fast != NULL && fast->next != NULL) {
        slow = slow->next;
        fast = fast->next->next;
        
        if (slow == fast) 
        {
            // 步骤二：发现环，寻找入口
            // 1. 定义两个指针，index1在头，index2在相遇点
            struct ListNode *index1 = head;
            struct ListNode *index2 = slow;
            // 2. 两人每次都走一步，直到相遇
            while (index1 != index2) 
            {
                index1 = index1->next;
                index2 = index2->next;
            } 
            // 3. 相遇点即为环入口
            return index1; 
        }
    }
    return NULL;
}

3. 数学推导（图解逻辑）

设：

L L L = 头节点到环入口的距离。
C C C = 环的长度。
N N N = 环入口到相遇点的距离（沿运行方向）。
相遇时，慢指针在环内走了 N N N 的距离。

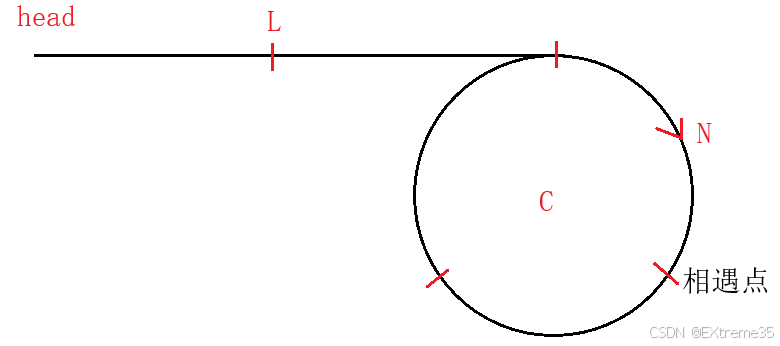
推导过程：

慢指针 slow 走的距离 ： S s l o w = L + N S_{slow} = L + N Sslow=L+N
(注意：通常慢指针在入环第一圈内就会被追上)
快指针 fast 走的距离 ： S f a s t = L + N + n C S_{fast} = L + N + nC Sfast=L+N+nC
( n n n 是快指针在环内绕的圈数，且 n ≥ 1 n \ge 1 n≥1)
速度关系 ：快指针速度是慢指针的 2 倍。
2 × ( L + N ) = L + N + n C 2 \times (L + N) = L + N + nC 2×(L+N)=L+N+nC
化简公式 ：
2 L + 2 N = L + N + n C 2L + 2N = L + N + nC 2L+2N=L+N+nC
L + N = n C L + N = nC L+N=nC
L = n C − N L = nC - N L=nC−N
关键变换 ：

为了直观理解，我们将 n C nC nC 拆解为 ( n − 1 ) C + C (n-1)C + C (n−1)C+C：
L = ( n − 1 ) C + ( C − N ) L = (n-1)C + (C - N) L=(n−1)C+(C−N)

公式含义解析：

L L L 是从头走到入口的距离。
( C − N ) (C - N) (C−N) 恰好是从相遇点继续往前走，回到环入口的距离。
( n − 1 ) C (n-1)C (n−1)C 表示在环里转了 n − 1 n-1 n−1 圈（这对最终位置没有影响）。

结论：从头节点出发走 L L L 步，和从相遇点出发走 L L L 步（实际上是转几圈后走了 C − N C-N C−N），会同时到达环入口。

第三部分：复杂度

时间复杂度 ： O ( N ) O(N) O(N)。
- 判断有环时，快慢指针在环内移动次数不会超过环的长度，总步数与节点数 N N N 线性相关。
- 寻找入口时，同样是线性遍历。
空间复杂度 ： O ( 1 ) O(1) O(1)。
- 只使用了 slow, fast 等几个指针变量，没有使用额外的数据结构。

算法深潜：链表中的生死之环（LeetCode 141 & 142 详解）

目录

第一部分：判断链表是否有环

1. 问题描述

2. 核心思路：快慢指针法

3. 数学证明（重点）

Q1: 为什么快指针走2步，慢指针走1步，两者一定会相遇？

Q2: 如果不按照当前设定走呢？还能保证相遇吗？

第二部分：寻找环的入口

1. 问题描述

2. 核心思路：双指针二次相遇

3. 数学推导（图解逻辑）

第三部分：复杂度