代码随想录 115.不同的子序列

思路：本题也是编辑距离类型问题。本题相当于只有删除操作，不考虑替换增加之类的。

动规五部曲：

1.确定dp数组（dp table）及其下标的含义：dp[i][j]表示以i - 1为结尾的s子序列中，出现以j - 1为结尾的t的个数为dp[i][j]。

2.确定递推公式：分为两种情况。

（1）s[i - 1]与t[j - 1]相等：dp[i][j]可以由两部分组成。

------一部分是用s[i - 1]来匹配，个数为dp[i - 1][j - 1]。即不需要考虑当前s子串和t子串的最后一位字母，所以只需要dp[i - 1][j - 1]。

------另一部分是不用s[i - 1]来匹配，个数为dp[i - 1][j]。

所以此时递推公式为dp[i][j] = dp[i - 1][j - 1] + dp[i - 1][j]。

（2）s[i - 1]与t[j - 1]不相等：dp[i][j]只有一部分组成，那就是不用s[i - 1]来匹配（模拟在s中删除这个元素），即：dp[i - 1][j]。此时递推公式为：dp[i][j] = dp[i - 1][j]。

为什么只考虑不用s[i - 1]来匹配的情况，而没有考虑不用t[j - 1]来匹配的情况？

因为是要求s中有多少个t，而不是求t中有多少个s，所以只考虑s中删除元素的情况。

3.dp数组如何初始化：

（1）从递推公式dp[i][j] = dp[i - 1][j - 1] + dp[i - 1][j]和dp[i][j] = dp[i - 1][j]可以看出，dp[i][j]是从上方和左上方推导而来，如下图所示。那么dp[i][0]和dp[0][j]一定是要初始化的。

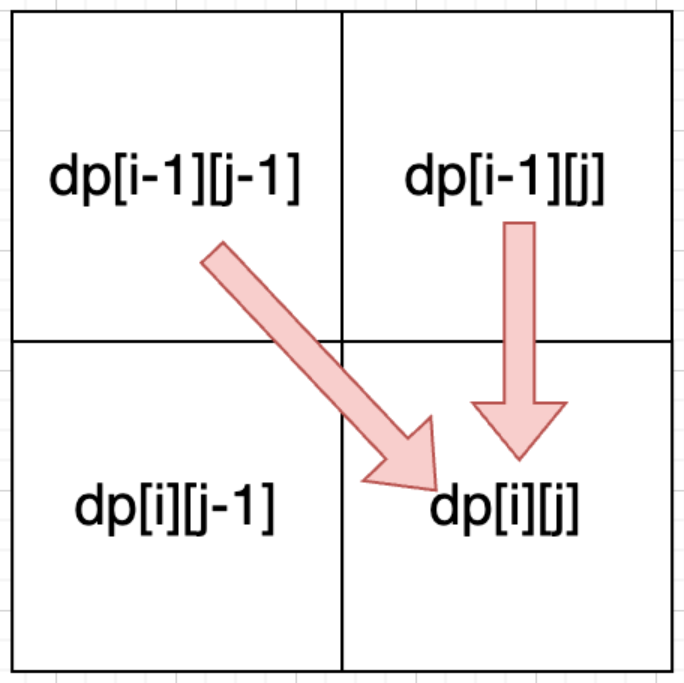
（2）初始化之前，先回顾dp[i][j]的定义。

------dp[i][0]表示：以i - 1为结尾的s可以随便删除元素，出现空字符串的个数。因此dp[i][0] = 1。

------dp[0][j]表示：空字符串s可以随便删除元素，出现以j - 1为结尾的字符串t的个数。因此dp[0][j] = 0，因为s无法变为t。

------dp[0][0]：dp[0][0]应该为1，因为空字符串s可以删除0个元素变成空字符串t。

4.确定遍历顺序：从递推公式dp[i][j] = dp[i - 1][j - 1] + dp[i - 1][j]和dp[i][j] = dp[i - 1][j]可以看出来，dp[i][j]是根据左上方和正上方推导出来的。所以遍历顺序为从上到下，从左到右，以保证dp[i][j]可以根据之前计算出的数值进行计算。代码如下所示。

cpp 复制代码

for (int i = 1; i <= s.size(); i++) {
    for (int j = 1; j <= t.size(); j++) {
        if (s[i - 1] == t[j - 1]) {
            dp[i][j] = dp[i - 1][j - 1] + dp[i - 1][j];
        } else {
            dp[i][j] = dp[i - 1][j];
        }
    }
}

5.举例推导dp数组：以s:"baegg"，t:"bag"为例，dp数组的状态如下所示。

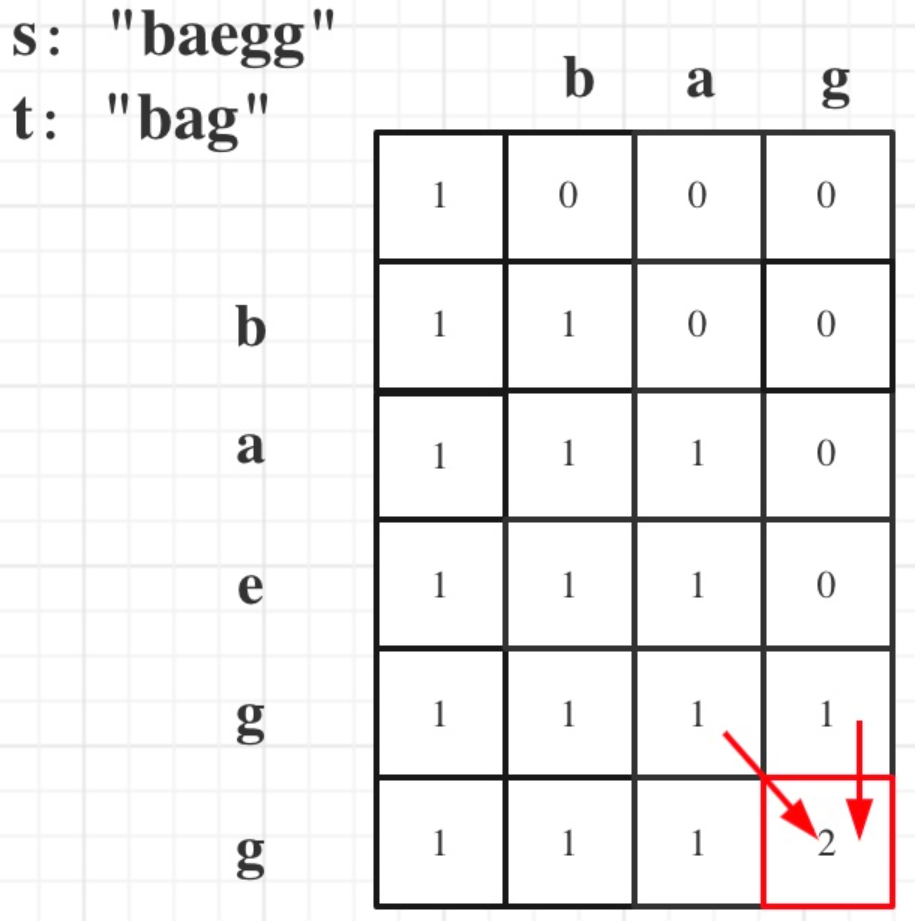
附代码：

java 复制代码

class Solution {
    public int numDistinct(String s, String t) {
        int len1 = s.length();
        int len2 = t.length();
        int[][] dp = new int[len1 + 1][len2 + 1];
        for(int i = 0;i < len1 + 1;i++){
            dp[i][0] = 1;
        }
        for(int i = 1;i < len1 + 1;i++){
            for(int j = 1;j < len2 + 1;j++){
                if(s.charAt(i - 1) == t.charAt(j - 1)){
                    //既可以使用主串s的最后一个字符s[i - 1]去匹配t的最后一个字符t[i - 1]
                    //也可以不使用主串s的最后一个字符s[i - 1]去匹配t的最后一个字符t[j - 1]
                    //这两种选择是互斥的，且覆盖了所有可能
                    dp[i][j] = dp[i - 1][j - 1] + dp[i - 1][j];
                }else{
                    //主串s的最后一个字符s[i - 1]不能用来匹配t的最后一个字符t[i - 1]
                    //因此必须用s[0..i - 2]去匹配t[0..j - 1]
                    dp[i][j] = dp[i - 1][j];
                }
            }
        }
        return dp[len1][len2];
    }
}