哈夫曼树和哈夫曼编码

[1. 什么是哈夫曼树和哈夫曼编码](#1. 什么是哈夫曼树和哈夫曼编码)
- [1.1 哈夫曼树](#1.1 哈夫曼树)
- [1.2 哈夫曼编码](#1.2 哈夫曼编码)
[2. 举个例子（如何构造哈夫曼树）](#2. 举个例子（如何构造哈夫曼树）)
[3. 哈夫曼编码的代码实现（C++）](#3. 哈夫曼编码的代码实现（C++）)

1. 什么是哈夫曼树和哈夫曼编码

1.1 哈夫曼树

哈夫曼树（Huffman Tree）是一种带权路径长度最短的二叉树（也叫最优二叉树）；哈夫曼编码是基于哈夫曼树生成的变长前缀编码，核心作用是 "数据压缩"------ 让出现频率高的字符用短编码，频率低的用长编码，大幅减少数据存储 / 传输体积。

打个生活化比方：

发短信时，"的""了""我" 这些高频字用 1 个字符（如 "0"），"疆""霾" 这些低频字用 3 个字符（如 "110"），整体短信字数会少很多；

哈夫曼树就是用来 "分配编码长度" 的规则，哈夫曼编码就是最终给每个字符定的 "长短码"。

1.2 哈夫曼编码

在哈夫曼编码之前，原始方法使用等长编码，即每个字符串使用相等长度的编码，这样会导致额外需要传输一部分数据，在高速要求下可能会造成一定的额外开销，哈夫曼编码不等长，即生成的编码是长度最短的非歧义的编码。

哈夫曼编码是根据哈夫曼树而形成的编码，左边的置为0，右边置为1（这个没有强制要求，只需要在同一个哈夫曼树中使用同样的规则即可，大众化的编码规则是左0右1，本文也以这个为例讲解）

**注意：**生成的哈夫曼树以及哈夫曼编码可能不唯一，但所有编码的总长度一定为最短且解码时无歧义。

哈夫曼编码需要编码的节点一定是在叶子节点

2. 举个例子(如何构造哈夫曼树)

字符串：AABCADCEB

先统计字母的出现次数：

A->3

B->2

C->2

D->1

E->1

每次选出最小的两个值作为基础节点进行构建，出现重复数量超过两个也无妨，随机选取两个即可，之后这两个节点被一个新的更大的两个相加的节点代替

先选择D和E构建，此时D和E转化为一个整体节点为2。

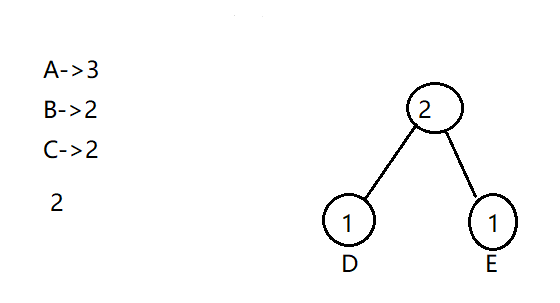
此时BC和DE的整体节点都为2，任选两个，这边选取B和C

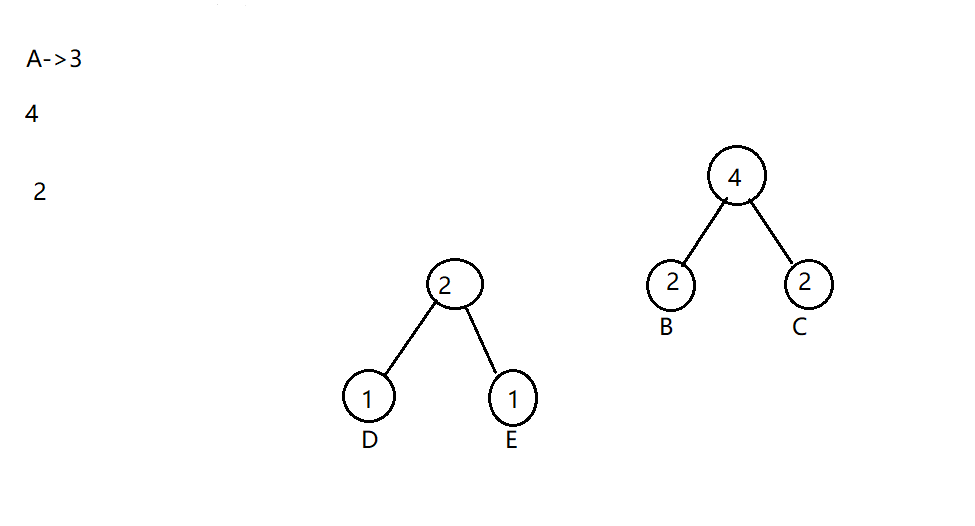
选择最小的A和DE结合节点，最后和BC的结合节点合并，左边填充0，右边填充1，最终完整的哈夫曼树如下

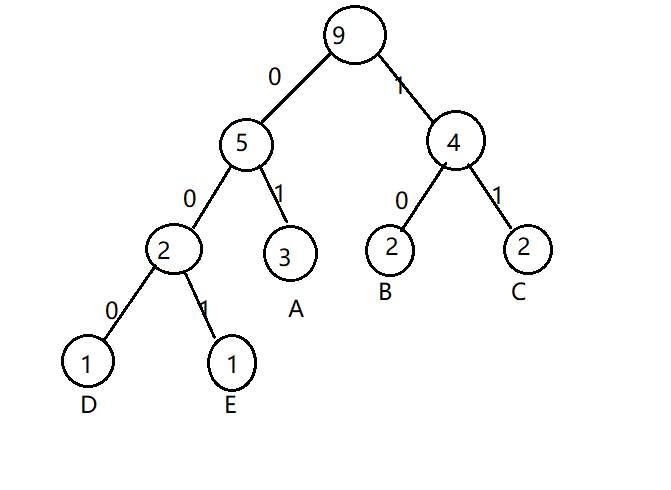
可以得到哈夫曼编码：

A:01

B:10

C:11

D:000

E:001

3 哈夫曼编码的代码实现（C++）

cpp 复制代码

#include <iostream>
#include <queue>
#include <unordered_map>
#include <vector>
#include <string>
#include <algorithm>

using namespace std;

// 哈夫曼树节点结构体
struct HuffmanNode {
    char ch;                // 字符（仅叶子节点有效）
    int weight;             // 权值（字符频率）
    HuffmanNode *left;      // 左子节点
    HuffmanNode *right;     // 右子节点

    // 构造函数
    HuffmanNode(char c = '\0', int w = 0, HuffmanNode *l = nullptr, HuffmanNode *r = nullptr)
        : ch(c), weight(w), left(l), right(r) {}

    // 重载小于运算符（优先队列默认大顶堆，需改为小顶堆）
    bool operator<(const HuffmanNode &other) const {
        return weight > other.weight; // 权值小的优先出队
    }
};

// 递归生成哈夫曼编码（左0右1）
void generateHuffmanCode(HuffmanNode *root, string code, unordered_map<char, string> &huffmanCode) {
    if (root == nullptr) return;

    // 叶子节点（对应具体字符），记录编码
    if (root->left == nullptr && root->right == nullptr) {
        huffmanCode[root->ch] = code;
        return;
    }

    // 递归遍历左右子树
    generateHuffmanCode(root->left, code + "0", huffmanCode);
    generateHuffmanCode(root->right, code + "1", huffmanCode);
}

// 释放哈夫曼树内存（避免内存泄漏）
void deleteHuffmanTree(HuffmanNode *root) {
    if (root == nullptr) return;
    deleteHuffmanTree(root->left);
    deleteHuffmanTree(root->right);
    delete root;
}

int main() {
    // 1. 输入字符串
    string inputStr;
    cout << "请输入需要编码的字符串：";
    getline(cin, inputStr);
    if (inputStr.empty()) {
        cout << "输入字符串不能为空！" << endl;
        return 1;
    }

    // 2. 统计字符频率（权值）
    unordered_map<char, int> charFreq;
    for (char ch : inputStr) {
        charFreq[ch]++;
    }

    // 3. 构建优先队列（小顶堆），初始化叶子节点
    priority_queue<HuffmanNode> pq;
    for (auto &pair : charFreq) {
        pq.emplace(pair.first, pair.second);
    }

    // 4. 构建哈夫曼树
    while (pq.size() > 1) {
        // 取出权值最小的两个节点
        HuffmanNode *left = new HuffmanNode(pq.top());
        pq.pop();
        HuffmanNode *right = new HuffmanNode(pq.top());
        pq.pop();

        // 合并为新节点（权值=两节点权值之和，无字符）
        HuffmanNode mergeNode('\0', left->weight + right->weight, left, right);
        pq.push(mergeNode);
    }

    // 哈夫曼树根节点
    HuffmanNode *root = new HuffmanNode(pq.top());
    pq.pop();

    // 5. 生成每个字符的哈夫曼编码
    unordered_map<char, string> huffmanCode;
    generateHuffmanCode(root, "", huffmanCode);

    // 6. 输出每个字符的哈夫曼编码
    cout << "\n=== 字符哈夫曼编码表 ===" << endl;
    for (auto &pair : huffmanCode) {
        cout << "字符 '" << pair.first << "' (频率：" << charFreq[pair.first] << ")：" << pair.second << endl;
    }

    // 7. 生成输入字符串的完整编码
    string strCode;
    for (char ch : inputStr) {
        strCode += huffmanCode[ch];
    }
    cout << "\n=== 输入字符串的哈夫曼编码 ===" << endl;
    cout << inputStr << " → " << strCode << endl;

    // 8. 释放内存
    deleteHuffmanTree(root);

    return 0;
}

4. 哈夫曼编码的应用场景：

1：归档压缩格式：

ZIP/GZIP：ZIP 格式的默认压缩算法（Deflate 算法）由 "LZ77/LZ78 字典压缩 + 哈夫曼编码" 组成 ------ 先通过字典压缩消除重复数据，再用哈夫曼编码对字典索引和原始数据进一步压缩，最终减少文件体积 30%~70%；GZIP（常用于 Linux 文件压缩、HTTP 传输压缩）同样基于 Deflate 算法，哈夫曼编码是其最终压缩环节。

7-ZIP*：支持多种压缩算法，其中 "Deflate64""LZMA2" 等核心算法均会搭配哈夫曼编码优化压缩率，尤其对文本、日志、源代码等字符重复率高的文件效果显著。
2：文档文本压缩：

PDF 文件：PDF 中的文本内容、图片元数据等会通过哈夫曼编码压缩，减少 PDF 文件的存储大小和传输时间（比如一篇 10MB 的纯文本 PDF，压缩后可降至 2~3MB）。

TXT / 日志文件：纯文本文件（如服务器日志、配置文件）中高频字符（如空格、换行、字母 "e""a"）占比极高，哈夫曼编码能针对性压缩，压缩率通常在 40%~60%。
3:图片压缩

PNG 格式：PNG 是无损图片格式，其压缩流程为 "预测编码 + 差分编码 + 哈夫曼编码"------ 先通过预测编码减少像素冗余，再用哈夫曼编码对编码后的数据流压缩，确保图片质量无损的同时，减少文件体积（比如一张 100KB 的 PNG 图标，压缩后可降至 30~50KB）。

JPEG 格式：JPEG 是有损压缩，但对 "离散余弦变换（DCT）后的系数""图片元数据（如分辨率、色深）" 会用哈夫曼编码做无损压缩，进一步降低文件大小（JPEG 的压缩率中，约 10%~20% 来自哈夫曼编码）。
4:音频压缩

MP3 格式：MP3 是有损音频格式，其编码流程中，对 "量化后的频谱系数" 会用哈夫曼编码压缩（利用系数的分布特性，高频系数多为 0，低频系数重复率高），在不明显影响音质的前提下，将音频文件体积压缩至原始 WAV 格式的 1/10~1/15。

FLAC 格式：FLAC 是无损音频格式，核心压缩算法包含 "线性预测编码 + 哈夫曼编码"，能在完全还原音质的前提下，将音频文件体积压缩至原始的 50%~70%。