SAPO:软自适应策略优化------大语言模型强化学习训练的稳定新范式
强化学习已成为提升大语言模型推理能力的关键技术,但训练过程中的不稳定性问题长期困扰着研究者。阿里巴巴Qwen团队最新提出的SAPO(Soft Adaptive Policy Optimization)方法通过引入温度控制的软门控机制,巧妙地平衡了训练稳定性与学习效率。本文将深入解析这一突破性方法如何在保持序列连贯性的同时实现token级自适应,为大规模语言模型的RL训练开辟新路径。
论文标题:Soft Adaptive Policy Optimization
来源:arXiv:2511.20347v2 + https://arxiv.org/abs/2511.20347
PS: 整理了LLM、量化投资、机器学习方向的学习资料,关注同名公众号 「 AI极客熊 」 即刻免费解锁
文章核心
研究背景:
强化学习在大语言模型训练中发挥着日益重要的作用,特别是在数学推理、编程和多模态理解等挑战性任务中。基于组的策略优化方法已成为实用方案:每个查询采样多个响应,组内归一化序列级奖励,并通过当前策略与行为策略间的重要性比率加权策略更新。然而,在Mixture-of-Experts(MoE)模型中,token级重要性比率往往表现出高方差------路由异构性和长响应会放大token间的偏差,这种方差增加了不稳定更新的可能性。
研究问题:
- 高方差问题:token级重要性比率的高方差导致更新不稳定,尤其在MoE模型中更为严重
- 硬截断局限性:现有方法如GRPO和GSPO使用硬截断,难以在稳定性和有效学习间取得平衡
- 样本效率低下:当序列包含少数高度离策略token时,GSPO会抑制该序列的所有梯度,降低样本效率
主要贡献:
- 软门控机制:提出温度控制的软门控替代硬截断,实现连续信任区域,保持近策略梯度的同时平滑衰减离策略更新
- 非对称温度设计:针对正负token采用不同温度参数,使负token梯度衰减更快,减少训练不稳定性
- 序列连贯与token自适应:在温和条件下表现为序列级方法,在异质序列中保持token级适应性,选择性降权离群token
- 实证验证:在数学推理基准测试中展示出改进的训练稳定性和更高的Pass@1性能,并在Qwen3-VL模型系列训练中实现跨任务和模型规模的一致性能提升
方法论精要
SAPO的核心创新在于将传统的硬截断机制替换为温度控制的软门控函数。具体而言,SAPO最大化以下目标函数:
J ( θ ) = E q ∼ D , { y i } i = 1 G ∼ π θ o l d ( ⋅ ∣ q ) [ 1 G ∑ i = 1 G 1 ∣ y i ∣ ∑ t = 1 ∣ y i ∣ f i , t ( r i , t ( θ ) ) A ^ i , t ] J(\theta) = \mathbb{E}{q \sim D, \{y_i\}{i=1}^G \sim \pi_{\theta_{old}}(\cdot|q)} \left[ \frac{1}{G} \sum_{i=1}^G \frac{1}{|y_i|} \sum_{t=1}^{|y_i|} f_{i,t}(r_{i,t}(\theta)) \hat{A}_{i,t} \right] J(θ)=Eq∼D,{yi}i=1G∼πθold(⋅∣q)[G1∑i=1G∣yi∣1∑t=1∣yi∣fi,t(ri,t(θ))A^i,t]
其中, f i , t ( x ) = σ ( τ i , t ( x − 1 ) ) ⋅ 4 τ i , t f_{i,t}(x) = \sigma(\tau_{i,t}(x-1)) \cdot \frac{4}{\tau_{i,t}} fi,t(x)=σ(τi,t(x−1))⋅τi,t4, τ i , t = { τ p o s , if A ^ i , t > 0 τ n e g , otherwise \tau_{i,t} = \begin{cases} \tau_{pos}, \text{if } \hat{A}{i,t} > 0 \\ \tau{neg}, \text{otherwise} \end{cases} τi,t={τpos,if A^i,t>0τneg,otherwise, σ ( x ) = 1 / ( 1 + e − x ) \sigma(x) = 1/(1+e^{-x}) σ(x)=1/(1+e−x)为sigmoid函数。
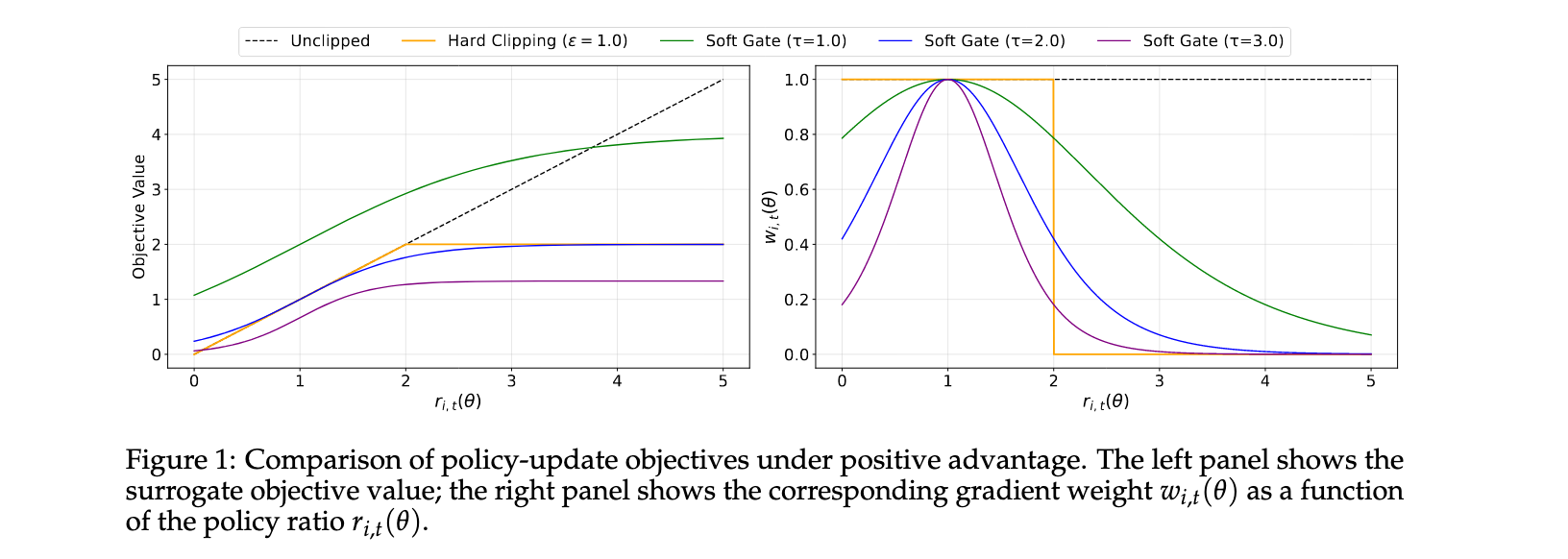
软门控机制的理论优势
与GSPO和GRPO相比,SAPO在两个关键维度上表现出优越性:
序列连贯性 :在温和条件(小步长更新和序列内token log-比率低分散)下,平均token门控收敛到平滑的序列级门控 g ( log s i ( θ ) ) = sech 2 ( τ i 2 log s i ( θ ) ) g(\log s_i(\theta)) = \text{sech}^2(\frac{\tau_i}{2}\log s_i(\theta)) g(logsi(θ))=sech2(2τilogsi(θ))。此时SAPO退化为类似GSPO的序列级表述,但使用连续信任区域替代GSPO的脆弱硬截断带。
Token级适应性:当序列包含少数高度离策略token时,GSPO会抑制该序列的所有梯度,而SAPO仅选择性地降权离群token,保留近策略token的学习信号,提高样本效率。相对GRPO,SAPO用平滑的温度控制缩放替代硬token级截断,提供更多信息量和稳定更新。
非对称温度设计的理论依据
SAPO的一个关键创新是为正负token设置不同温度参数。这一设计基于对token级梯度如何通过logits传播的理论分析:
∂ log π θ ( y i , t ∣ q , y i , < t ) A ^ i , t ∂ z v = { ( 1 − π θ ( y i , t ∣ q , y i , < t ) ) ⋅ A ^ i , t if v = y i , t − π θ ( v ∣ q , y i , < t ) ⋅ A ^ i , t otherwise \frac{\partial \log \pi_{\theta}(y_{i,t}|q,y_{i,<t}) \hat{A}{i,t}}{\partial z_v} = \begin{cases} (1-\pi{\theta}(y_{i,t}|q,y_{i,<t})) \cdot \hat{A}{i,t} & \text{if } v = y{i,t} \\ -\pi_{\theta}(v|q,y_{i,<t}) \cdot \hat{A}_{i,t} & \text{otherwise} \end{cases} ∂zv∂logπθ(yi,t∣q,yi,<t)A^i,t={(1−πθ(yi,t∣q,yi,<t))⋅A^i,t−πθ(v∣q,yi,<t)⋅A^i,tif v=yi,totherwise
正优势增加采样token的logit并降低所有未采样logits;负优势则相反,会提高许多未采样token的logit。在LLM的RL微调中,动作空间是大型词汇表(通常数十万token),而给定状态下的理想动作数量很少。因此,负梯度扩散到大量无关token上------虽然提供一定正则化效果,但也引入不稳定性,特别是在离策略场景中。
为此,SAPO为正负token使用不同温度并设置 τ n e g τ p o s \tau_{neg} \tau_{pos} τnegτpos,使负token上的梯度衰减更快,从而提高训练稳定性和性能。
理论连接与统一视角
从统一代理目标视角看,三种算法的差异主要体现在门控函数 f i , t ( ⋅ ) f_{i,t}(\cdot) fi,t(⋅)的选择上:
- SAPO : f i , t S A P O ( r i , t ( θ ) ) = 4 τ i σ ( τ i ( r i , t ( θ ) − 1 ) ) f^{SAPO}{i,t}(r{i,t}(\theta)) = \frac{4}{\tau_i} \sigma(\tau_i(r_{i,t}(\theta)-1)) fi,tSAPO(ri,t(θ))=τi4σ(τi(ri,t(θ)−1))
- GRPO : f i , t G R P O ( r i , t ( θ ) ; A ^ i ) = { min ( r i , t ( θ ) , 1 + ϵ ) A ^ i > ; 0 max ( r i , t ( θ ) , 1 − ϵ ) A ^ i ≤ 0 f^{GRPO}{i,t}(r{i,t}(\theta); \hat{A}i) = \begin{cases} \min(r{i,t}(\theta), 1+\epsilon) \hat{A}i \gt; 0 \\ \max(r{i,t}(\theta), 1-\epsilon) \hat{A}_i \leq 0 \end{cases} fi,tGRPO(ri,t(θ);A^i)={min(ri,t(θ),1+ϵ)A^i>;0max(ri,t(θ),1−ϵ)A^i≤0
- GSPO : f i , t G S P O ( r i , t ( θ ) ; A ^ i ) ≡ f i , t s e q ( s i , t ( θ ) ; A ^ i ) f^{GSPO}{i,t}(r{i,t}(\theta); \hat{A}i) \equiv f^{seq}{i,t}(s_{i,t}(\theta); \hat{A}_i) fi,tGSPO(ri,t(θ);A^i)≡fi,tseq(si,t(θ);A^i)
SAPO的token级软门控通过 σ ( x ) ( 1 − σ ( x ) ) = 1 4 sech 2 ( x / 2 ) \sigma(x)(1-\sigma(x)) = \frac{1}{4}\text{sech}^2(x/2) σ(x)(1−σ(x))=41sech2(x/2)性质,其导数为 f i , t S A P O ( r i , t ( θ ) ) = sech 2 ( τ i 2 ( r i , t ( θ ) − 1 ) ) f^{SAPO}{i,t}(r{i,t}(\theta)) = \text{sech}^2(\frac{\tau_i}{2}(r_{i,t}(\theta)-1)) fi,tSAPO(ri,t(θ))=sech2(2τi(ri,t(θ)−1)),在 r i , t ( θ ) = 1 r_{i,t}(\theta)=1 ri,t(θ)=1处达到峰值1,并随 r i , t ( θ ) r_{i,t}(\theta) ri,t(θ)偏离1而平滑衰减,实现软信任区域,防止梯度消失和过度大更新。
实验洞察
控制实验结果
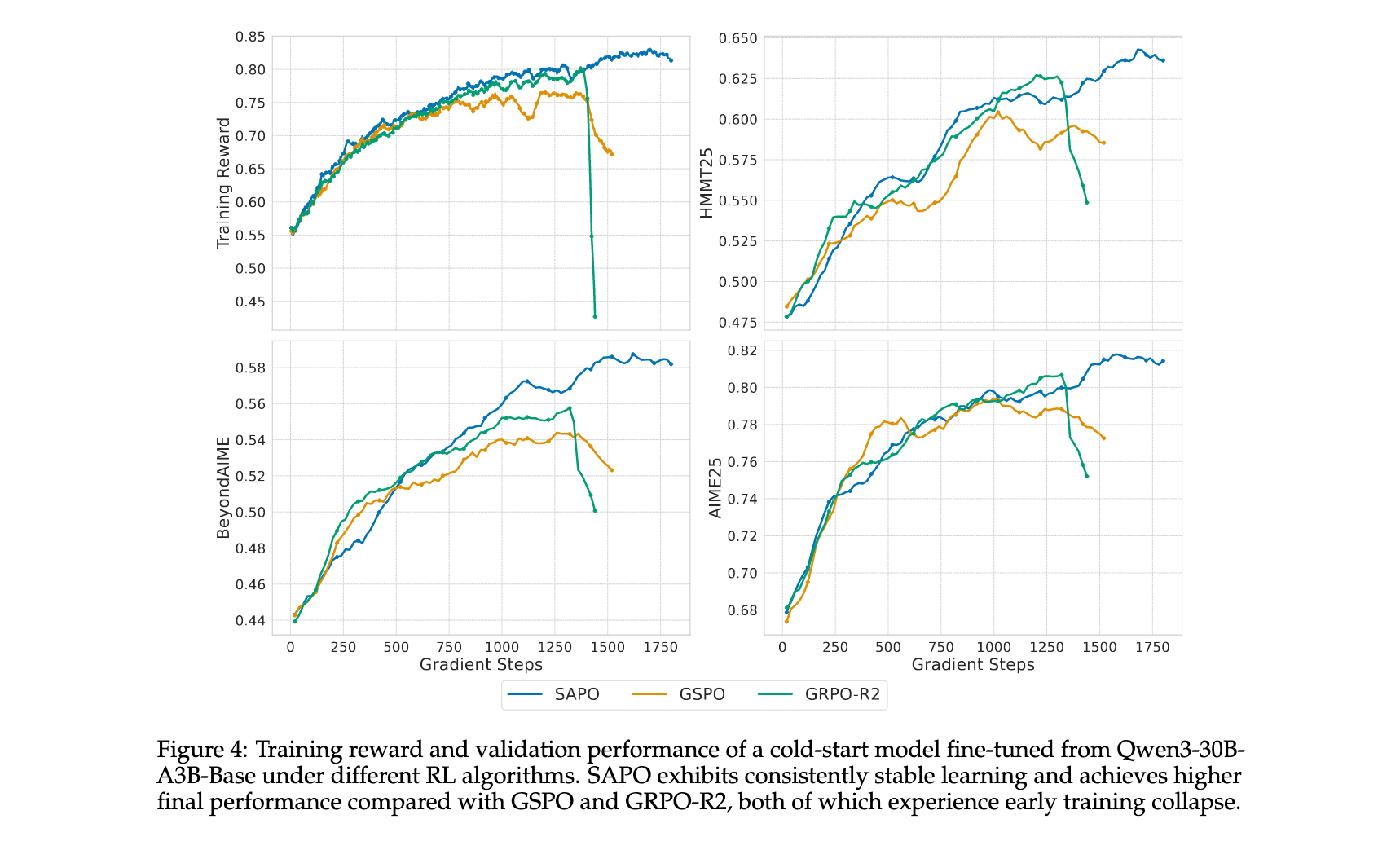
研究团队使用从Qwen3-30B-A3B-Base微调的冷启动模型在数学推理查询上进行实验。报告了AIME25、HMMT25和BeyondAIME基准上的训练奖励和验证性能(平均Pass@1,16个样本)。在RL训练期间,每批rollout数据被分为四个小批次进行梯度更新。对于SAPO,设置 τ p o s = 1.0 \tau_{pos}=1.0 τpos=1.0和 τ n e g = 1.05 \tau_{neg}=1.05 τneg=1.05。
实验结果显示,SAPO在所有基准测试上持续改进模型性能,与GSPO和GRPO-R2相比实现了更高的稳定性和更强的最终性能。虽然GSPO和GRPO-R2表现出早期训练崩溃,但SAPO保持了稳定的训练动态并最终获得优越性能。值得注意的是,SAPO不依赖路由回放来实现稳定或强性能,这改善了探索并减少了RL系统的工程开销。
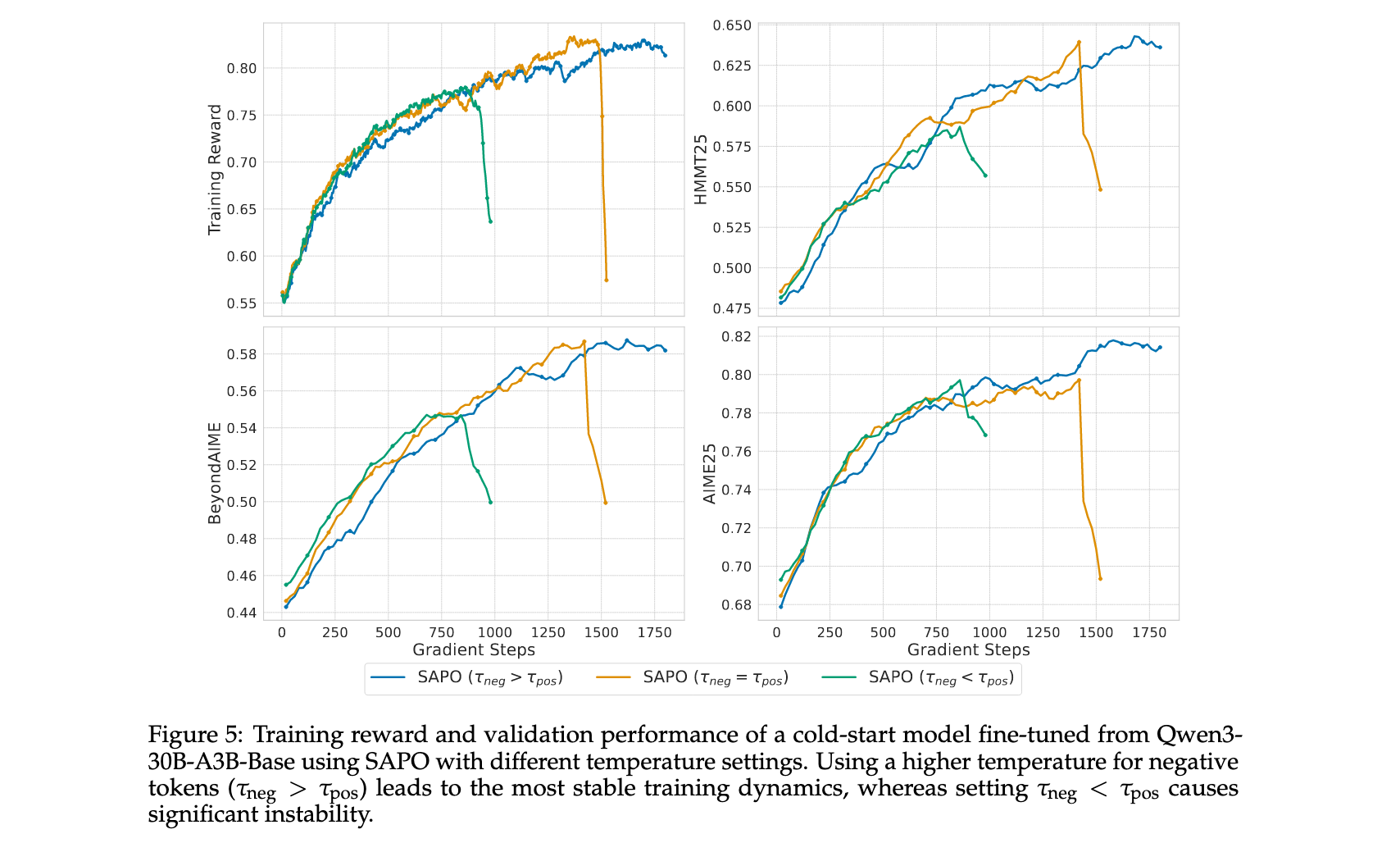
温度参数消融研究
为实证检验选择 τ n e g τ p o s \tau_{neg} \tau_{pos} τnegτpos的效果,研究评估了三种配置: τ n e g = 1.05 > τ p o s = 1.0 \tau_{neg}=1.05 > \tau_{pos}=1.0 τneg=1.05>τpos=1.0、 τ n e g = τ p o s = 1.0 \tau_{neg}=\tau_{pos}=1.0 τneg=τpos=1.0和 τ n e g = 0.95 < τ p o s = 1.0 \tau_{neg}=0.95 < \tau_{pos}=1.0 τneg=0.95<τpos=1.0。结果表明,当负token被分配更高温度( τ n e g = 1.05 \tau_{neg}=1.05 τneg=1.05)时训练最稳定,而当分配较低温度( τ n e g = 0.95 \tau_{neg}=0.95 τneg=0.95)时最不稳定。这些结果表明,与负token相关的梯度对训练不稳定性的贡献更强,而SAPO的非对称温度设计有效缓解了这一问题。
Qwen3-VL大规模训练验证
研究团队将SAPO应用于Qwen3-VL系列模型的训练,以评估其在实际大规模环境中的有效性。实验表明,SAPO在不同大小模型以及MoE和密集架构上都持续改进性能。训练涵盖广泛的文本和多模态任务,包括数学、编程和逻辑推理。为支持多任务学习,在每个批次内为每个任务维持固定采样比例。
为突出SAPO相对于GSPO和GRPO-R2的优势,研究从Qwen3-VL-30B-A3B的初步冷启动检查点开始评估所有三种强化学习算法。在四个基准上报告训练奖励和平均验证性能:AIME25(Pass@1,32个样本)、LiveCodeBenchv6(Pass@1,8个样本)、ZebraLogic和MathVision。结果显示,SAPO在整个训练过程中实现稳定的性能提升,并在相同计算预算下优于两个基线。
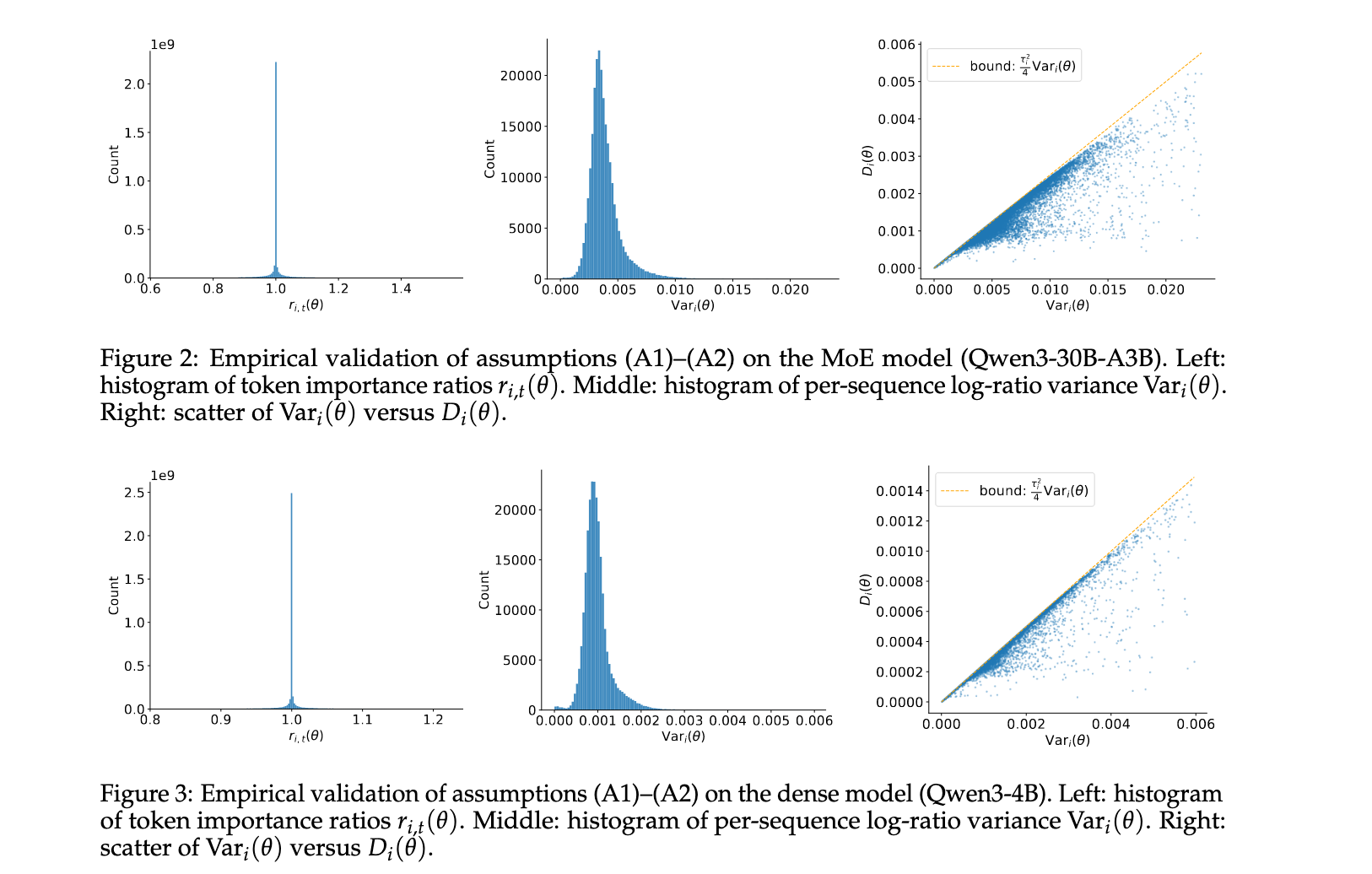
理论假设的实证验证
研究通过绘制MoE和密集模型的token比率 r i , t ( θ ) r_{i,t}(\theta) ri,t(θ)直方图和每序列log-比率方差 Var i ( θ ) \text{Var}i(\theta) Vari(θ)来实证评估小步长假设(A1)和低序列内分散假设(A2)。观察到 r i , t ( θ ) r{i,t}(\theta) ri,t(θ)在1附近急剧集中, Var i ( θ ) \text{Var}_i(\theta) Vari(θ)通常保持在0.02以下,MoE模型的分布相对较宽(可能反映了专家路由引起的异质性),而密集模型的集中度更紧。这些分布表明(A1)和(A2)在大多数情况下成立,特别是对于密集架构。此外,小的 D i ( θ ) D_i(\theta) Di(θ)直接意味着平均token门控可以很好地近似为序列级门控,支持了理论简化。