
判断链表有环?
我们在学习链表的时候,讲过如何判断链表是否有环的办法,讲解的时候是用的双指针的办法,如果有环,就会在这个环里相遇
算法步骤:
-
初始化两个指针,slow(每次走一步)和fast(每次走两步),都指向链表头部。
-
开始循环,直到fast为空或者fast的下一个节点为空(表示链表无环)或者slow和fast相遇(表示有环)。
-
如果fast或fast.next为null,说明链表无环,返回null。
-
如果slow和fast相遇,说明链表有环,进入步骤3。
-
-
当slow和fast相遇后,将其中一个指针(比如ptr1)重新指向链表头,另一个指针(ptr2)保持在相遇点。
然后两个指针每次同时移动一步,直到它们再次相遇。相遇的节点就是环的入口节点。
数学原理:
设链表头到环入口的距离为a,环入口到相遇点的距离为b,相遇点到环入口的距离为c。
则环的长度为b+c。
当slow和fast相遇时,slow走过的距离为a+b,fast走过的距离为a+b+n*(b+c),其中n是fast在环中绕的圈数。
因为fast的速度是slow的两倍,所以有:2(a+b) = a+b + n*(b+c) => a = (n-1)*(b+c) + c
这个公式说明,从链表头到环入口的距离a等于从相遇点到环入口的距离c加上n-1圈环的长度。
因此,当两个指针分别从链表头和相遇点以相同速度前进时,它们会在环入口处相遇。
变量定义:
-
a:链表头到环入口的距离 -
b:环入口到相遇点的距离 -
c:相遇点到环入口的距离(顺时针方向) -
n:快指针在相遇前在环中走的圈数 -
L:环的长度 = b + c
头 → 入口 → 相遇点 → 入口(完成环) 慢指针路程:a + b 快指针路程:a + b + n × L (因为快指针可能已经在环里转了n圈) 由于快指针速度是慢指针的2倍: 2 × (a + b) = a + b + n × L 化简得: a + b = n × L a = n × L - b a = (n - 1) × L + (L - b) a = (n - 1) × L + c
第一种方法:
两种情况的区别:
情况1:是快乐数(最终到达1)
text
序列:n → ... → 1 → 1 → 1 → ...
特点:1的平方和还是1,所以1是一个自循环
快慢指针轨迹:
慢指针:会慢慢走向1
快指针:会更快到达1
最终,它们会在1相遇情况2:不是快乐数(进入其他循环)
text
序列:n → ... → 4 → 16 → 37 → 58 → 89 → 145 → 42 → 20 → 4 → ...
特点:进入一个不包含1的循环
快慢指针轨迹:
慢指针:在循环中前进
快指针:在循环中更快前进
最终,它们会在循环中的某个点相遇(比如4或16等),但绝对不是1
java
class Solution {
public int sumOfSquares(int n) {
int sum = 0;
while (n > 0) {
int digit = n % 10;
sum += digit * digit;
n /= 10;
}
return sum;
}
public boolean isHappy(int n) {
int slow = n;
int fast = sumOfSquares(n);
while(slow != fast){
slow = sumOfSquares(slow);
fast = sumOfSquares(sumOfSquares(fast));
}
return slow == 1;
}
}鸽巢原理(抽屉原理):
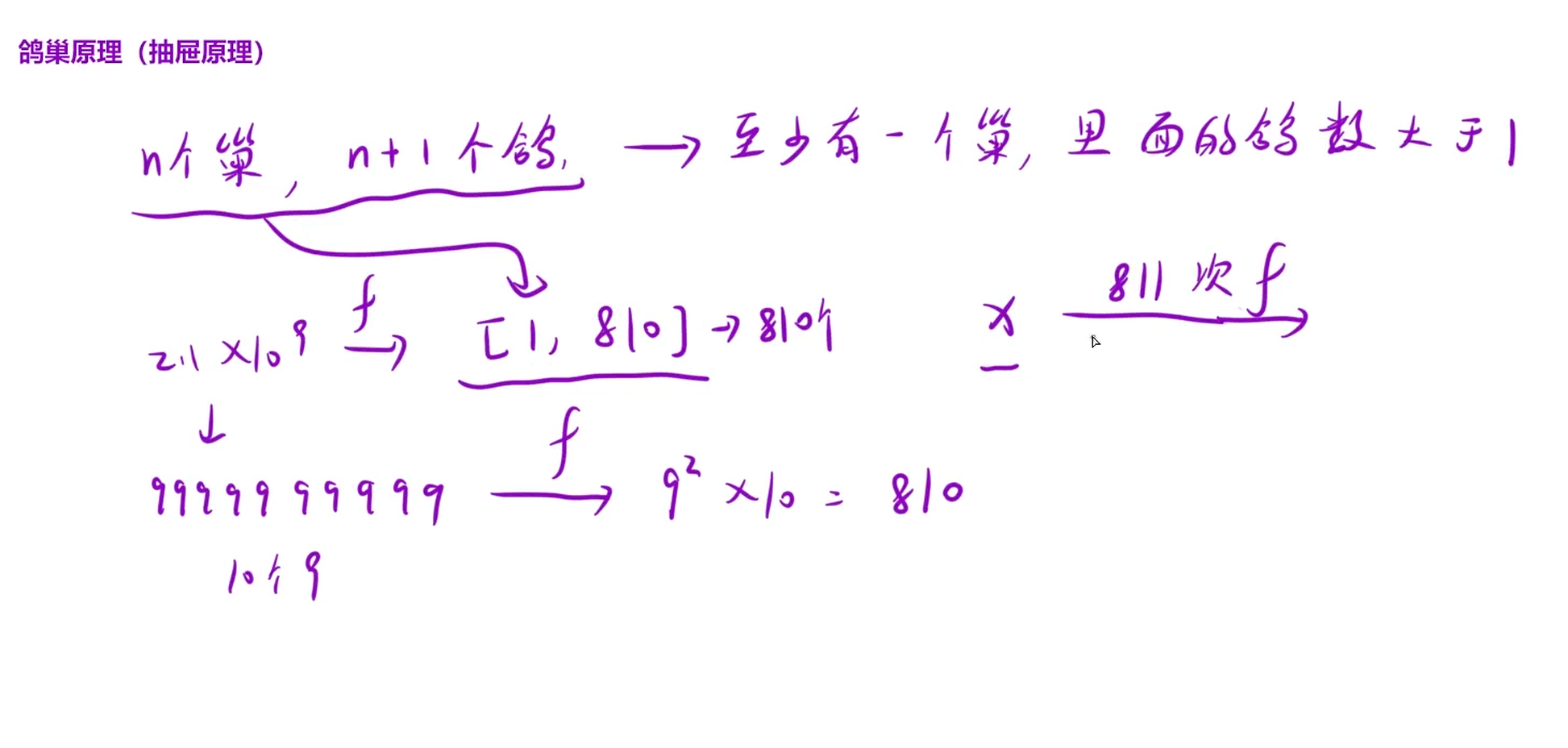
这个题有一个n 得取值范围:
我们直接换算成最大得
我们就简单得先计算多少位,是十位数,也就是2^10得九次方 ,那不如我们直接写成最大值以9来计算,十个9
10个9 进行每一位的平方和是810,也就是我们最大的值都小于十个9,所以我们进行的每一位平方和相加肯定也小于810
【1,810】就是我们的巢穴,我们接下来找鸽子,我们的巢穴是1-810
我们肯定超过这个810就会出现重复的的,也就是我们所说的进入环了
方法三:
核心逻辑:
-
巢穴数量:1,8101,810 共 810 个可能的平方和结果
-
鸽子数量:计算过程中产生的数字序列
-
鸽巢原理 :如果有 811 次计算(产生 811 个数字),而只有 810 个可能的结果,那么必然出现重复
-
关键判断:
-
如果在循环中出现 1 → 是快乐数
-
如果循环中不包含 1 → 不是快乐数
-
text
定理:对于函数 f,从任意 n 出发的序列要么: 1. 收敛到不动点 1 2. 进入一个不包含 1 的循环 证明: 假设存在一个包含 1 的循环,但不是 {1}。 那么循环中必有一个数 a ≠ 1,但 f(a) = 1。 但 f(a) = 1 意味着 a 的各位平方和为 1。 满足这个条件的 a 只能是:1, 10, 100, 1000, ... 计算这些数的平方和: 1 → 1 10 → 1 100 → 1 1000 → 1 ... 这些数最终都会进入 1→1 的自循环。 因此,任何包含 1 的循环只能是 {1}。
想象这样的序列:
... → x → 1 → y → ... → x → ...
从 1 开始:1 → f(1) = 1,不可能得到 y ≠ 1
所以一旦到达 1,就永远卡在 1 了
java
class Solution {
public int sumOfSquares(int n) {
int sum = 0;
while (n > 0) {
int digit = n % 10;
sum += digit * digit;
n /= 10;
}
return sum;
}
public boolean isHappy(int n) {
Set<Integer> seen = new HashSet<>();
while (n != 1) {
n = sumOfSquares(n);
if (seen.contains(n)) {
return false;
}
seen.add(n);
}
return true;
}
}