1. 从前序与中序遍历序列构造二叉树
题目描述
给定两个整数数组 preorder 和 inorder ,其中 preorder 是二叉树的先序遍历 , inorder 是同一棵树的中序遍历,请构造二叉树并返回其根节点。
示例 1:
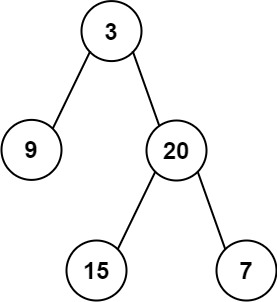
输入: preorder = [3,9,20,15,7], inorder = [9,3,15,20,7]
输出: [3,9,20,null,null,15,7]示例 2:
输入: preorder = [-1], inorder = [-1]
输出: [-1]提示:
1 <= preorder.length <= 3000inorder.length == preorder.length-3000 <= preorder[i], inorder[i] <= 3000preorder和inorder均 无重复 元素inorder均出现在preorderpreorder保证 为二叉树的前序遍历序列inorder保证 为二叉树的中序遍历序列
思路分析
利用先序(根→左→右)和中序(左→根→右)遍历特性:
- 先序首元素为根节点;
- 中序中根节点左侧是左子树、右侧是右子树;
- 递归拆分左右子树的先序 / 中序区间,构建子树。通过值→索引映射表快速定位根节点在中序的位置,避免遍历,提升效率。
代码实现
cpp
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* struct TreeNode *left;
* struct TreeNode *right;
* };
*/
// 辅助函数:递归构建二叉树
struct TreeNode* build(int* preorder, int preStart, int preEnd,
int* inorder, int inStart, int inEnd,
int* indexMap) {
// 递归终止条件:序列为空
if (preStart > preEnd || inStart > inEnd) {
return NULL;
}
// 先序序列第一个元素是根节点
int rootVal = preorder[preStart];
struct TreeNode* root = (struct TreeNode*)malloc(sizeof(struct TreeNode));
root->val = rootVal;
root->left = NULL;
root->right = NULL;
// 找到根节点在中序序列中的索引
int rootIndex = indexMap[rootVal + 3000]; // 偏移3000处理负数
// 左子树的节点个数
int leftSize = rootIndex - inStart;
// 递归构建左子树
root->left = build(preorder, preStart + 1, preStart + leftSize,
inorder, inStart, rootIndex - 1, indexMap);
// 递归构建右子树
root->right = build(preorder, preStart + leftSize + 1, preEnd,
inorder, rootIndex + 1, inEnd, indexMap);
return root;
}
struct TreeNode* buildTree(int* preorder, int preorderSize, int* inorder, int inorderSize) {
// 构建值到索引的映射表(处理-3000~3000的范围)
int indexMap[6001] = {0}; // 6001 = 3000 - (-3000) + 1
for (int i = 0; i < inorderSize; i++) {
indexMap[inorder[i] + 3000] = i;
}
// 递归构建二叉树
return build(preorder, 0, preorderSize - 1, inorder, 0, inorderSize - 1, indexMap);
}2.从中序与后序遍历序列构造二叉树
题目描述
给定两个整数数组 inorder 和 postorder ,其中 inorder 是二叉树的中序遍历, postorder 是同一棵树的后序遍历,请你构造并返回这颗 二叉树 。
示例 1:

输入:inorder = [9,3,15,20,7], postorder = [9,15,7,20,3]
输出:[3,9,20,null,null,15,7]示例 2:
输入:inorder = [-1], postorder = [-1]
输出:[-1]提示:
1 <= inorder.length <= 3000postorder.length == inorder.length-3000 <= inorder[i], postorder[i] <= 3000inorder和postorder都由 不同 的值组成postorder中每一个值都在inorder中inorder保证是树的中序遍历postorder保证是树的后序遍历
思路分析
利用后序(左→右→根)和中序(左→根→右)遍历特性:
- 后序尾元素为根节点;
- 中序中根节点左侧是左子树、右侧是右子树;
- 递归拆分左右子树的中序 / 后序区间,构建子树。同样用值→索引映射表快速定位根节点,优化查找效率。
代码实现
cpp
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* struct TreeNode *left;
* struct TreeNode *right;
* };
*/
// 辅助递归函数:构建二叉树
struct TreeNode* build(int* inorder, int inStart, int inEnd,
int* postorder, int postStart, int postEnd,
int* indexMap) {
// 递归终止条件:序列无节点
if (inStart > inEnd || postStart > postEnd) {
return NULL;
}
// 后序序列最后一个元素是根节点
int rootVal = postorder[postEnd];
struct TreeNode* root = (struct TreeNode*)malloc(sizeof(struct TreeNode));
root->val = rootVal;
root->left = NULL;
root->right = NULL;
// 找到根节点在中序序列中的索引
int rootIndex = indexMap[rootVal + 3000]; // 偏移3000处理负数
// 左子树的节点个数
int leftSize = rootIndex - inStart;
// 递归构建左子树
root->left = build(inorder, inStart, rootIndex - 1,
postorder, postStart, postStart + leftSize - 1,
indexMap);
// 递归构建右子树
root->right = build(inorder, rootIndex + 1, inEnd,
postorder, postStart + leftSize, postEnd - 1,
indexMap);
return root;
}
struct TreeNode* buildTree(int* inorder, int inorderSize, int* postorder, int postorderSize) {
// 构建值到中序索引的映射表(处理-3000~3000的范围)
int indexMap[6001] = {0}; // 6001 = 3000 - (-3000) + 1
for (int i = 0; i < inorderSize; i++) {
indexMap[inorder[i] + 3000] = i;
}
// 递归构建二叉树
return build(inorder, 0, inorderSize - 1,
postorder, 0, postorderSize - 1,
indexMap);
}总结
两类问题核心逻辑一致:
- 从遍历序列中定位根节点(先序首 / 后序尾);
- 借助中序拆分左右子树区间;
- 递归构建子树,映射表优化根节点查找,时间复杂度 O (n),空间复杂度 O (n)。差异仅在于根节点位置和后序序列的区间拆分规则,核心是利用遍历特性拆分递归区间。