[认知计算] 循环神经网络
个人导航
知乎:https://www.zhihu.com/people/byzh_rc
CSDN:https://blog.csdn.net/qq_54636039
注:本文仅对所述内容做了框架性引导,具体细节可查询其余相关资料or源码
参考文章:各方资料
目录
- [[认知计算] 循环神经网络](#[认知计算] 循环神经网络)
- 个人导航
- 序列数据
- [RNN: Recurrent Neural Network](#RNN: Recurrent Neural Network)
- [LSTM: Long Short-term Memory](#LSTM: Long Short-term Memory)
-
- 与RNN的不同之处
- 结构拆解
-
-
- [1.细胞状态cell state](#1.细胞状态cell state)
- [2.遗忘门forget gate](#2.遗忘门forget gate)
- [3.输入门input gate](#3.输入门input gate)
- [4.输出门output gate](#4.输出门output gate)
- [5.更新旧细胞状态 C i − 1 → C i C_{i-1} \rightarrow C_i Ci−1→Ci](#5.更新旧细胞状态 C i − 1 → C i C_{i-1} \rightarrow C_i Ci−1→Ci)
-
- 更多架构
-
-
- [1.窥视孔LSTM(poophole LSTM)](#1.窥视孔LSTM(poophole LSTM))
- 2.耦合(couple)遗忘门与输入门
- [3.门控循环单元GRU(Gated Recurrent Unit)](#3.门控循环单元GRU(Gated Recurrent Unit))
-
序列数据
时间序列数据是指在不同时间点收集的数据
特征:后一个数据与前一个的数据相关
- 语音识别: speech recognition
- 音乐生成: music generation
- 情感分类: sentiment classification
- DNA序列分析: DNA sequence analysis
- 机器翻译: machine translation
- 视频活动识别: video activity recognition
- 命名实体识别: name entity recognition
RNN: Recurrent Neural Network
- 权重矩阵 W a a W_{aa} Waa 在整个时间步上是共享的
- 权重矩阵 W a x W_{ax} Wax 在整个时间步上是共享的
- 权重矩阵 W y a W_{ya} Wya 在整个时间步上是共享的
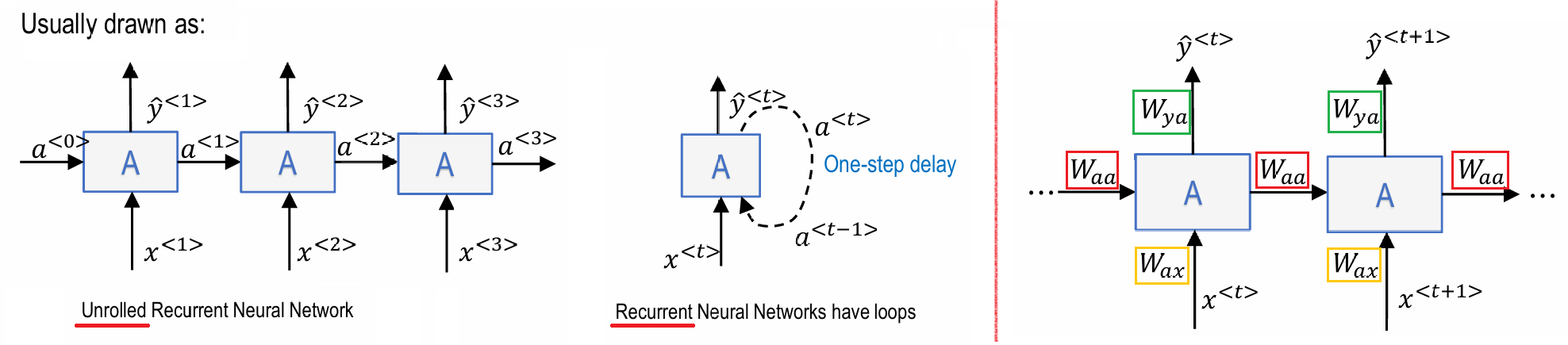
典型结构
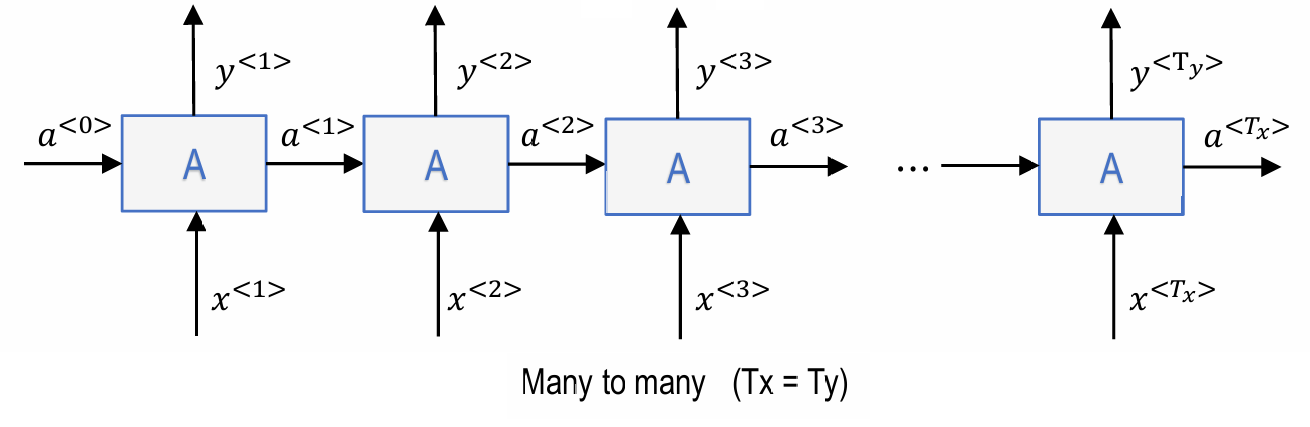
1.many to many
命名实体识别(name entity recognition):
-> 一个输入实时产生一个输出
-> 输入长度=输出长度
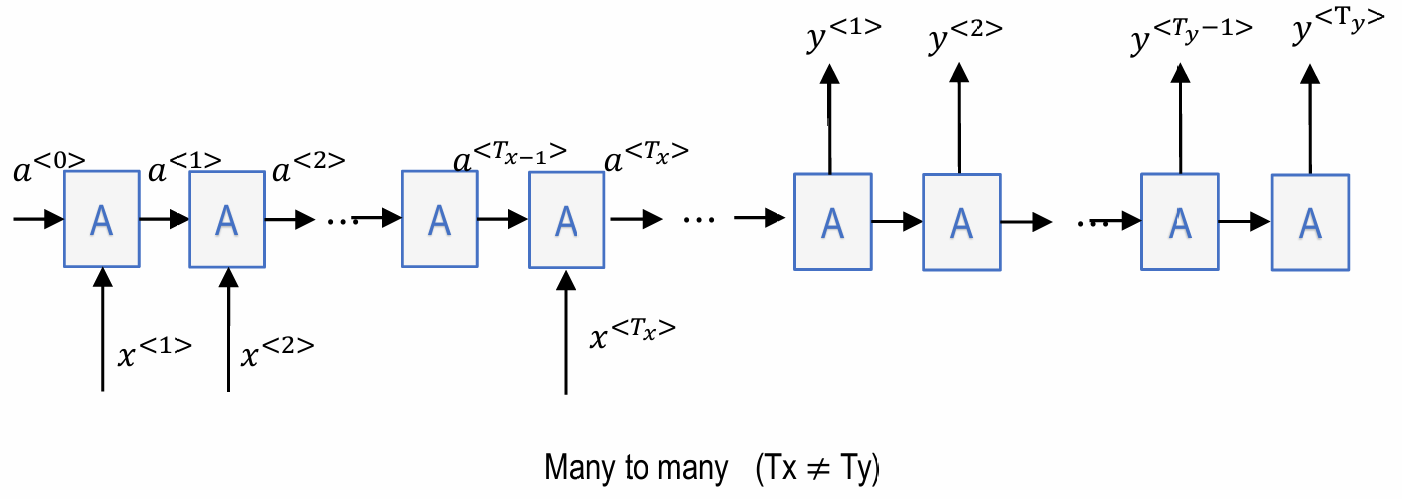
机器翻译(machine translation), 视频字幕生成(video captioning):
-> 先逐一捕获所有输入信息, 再逐一输出
-> 输入长度!=输出长度
2.many to one
情感分类(sentiment classification), 视频活动识别(video activity recognition):
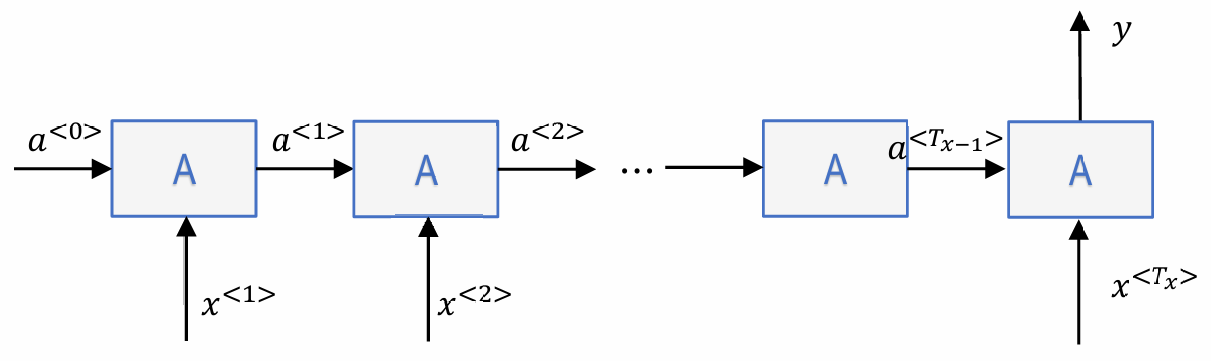
3.one to many
音乐生成(music generation), 图像标题生成(image captioning):
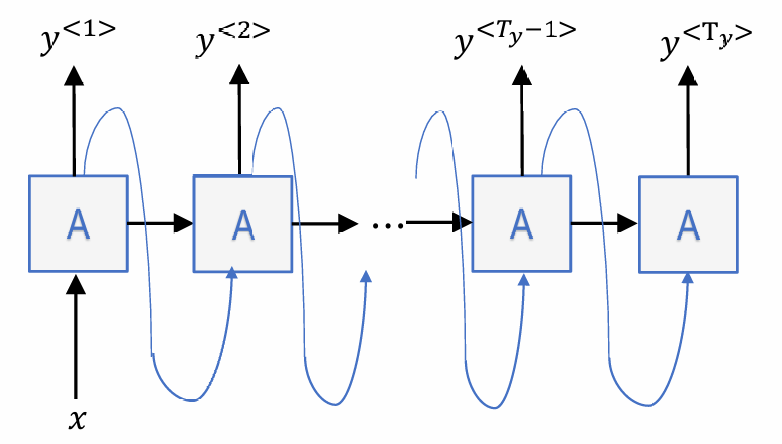
更多架构
1. 双向RNN(Bi-directional RNN)
既有从左到右提取的信息, 还有从右到左提取的信息
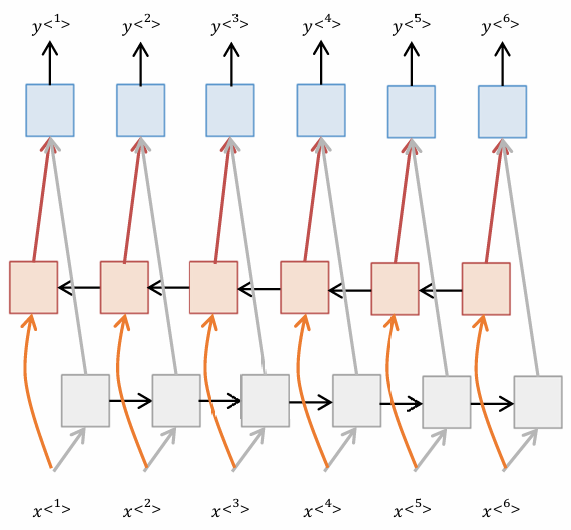
2.金字塔RNN(Pyramid RNN)
适合捕捉序列中不同时间尺度的模式
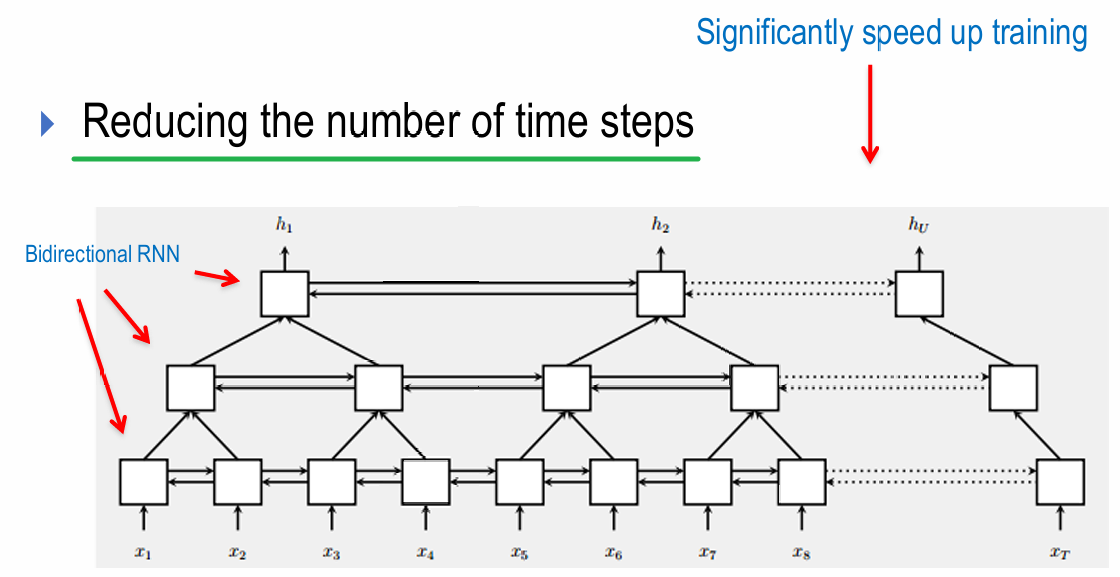
具体计算
| 符号 | 含义与说明 |
|---|---|
| t t t | 时间步编号, t = 1 , 2 , ... , T y t = 1, 2, \dots, T_y t=1,2,...,Ty |
| x ⟨ t ⟩ x^{\langle t \rangle} x⟨t⟩ | 第 t t t 个时间步的输入向量 |
| a ⟨ t ⟩ a^{\langle t \rangle} a⟨t⟩ | 第 t t t 个时间步的隐藏状态(激活值) |
| a ⟨ 0 ⟩ a^{\langle 0 \rangle} a⟨0⟩ | 初始隐藏状态,通常设为零向量 |
| y ^ ⟨ t ⟩ \hat{y}^{\langle t \rangle} y^⟨t⟩ | 第 t t t 个时间步的预测输出 |
| y ⟨ t ⟩ y^{\langle t \rangle} y⟨t⟩ | 第 t t t 个时间步的真实标签(one‑hot 向量或二分类标签) |
| W a x W_{ax} Wax | 输入 x ⟨ t ⟩ x^{\langle t \rangle} x⟨t⟩ 到隐藏状态 a ⟨ t ⟩ a^{\langle t \rangle} a⟨t⟩ 的权重矩阵 |
| W a a W_{aa} Waa | 前一隐藏状态 a ⟨ t − 1 ⟩ a^{\langle t-1 \rangle} a⟨t−1⟩ 到当前隐藏状态 a ⟨ t ⟩ a^{\langle t \rangle} a⟨t⟩ 的权重矩阵 |
| W y a W_{ya} Wya | 隐藏状态 a ⟨ t ⟩ a^{\langle t \rangle} a⟨t⟩ 到输出 y ^ ⟨ t ⟩ \hat{y}^{\langle t \rangle} y^⟨t⟩ 的权重矩阵 |
| b a b_a ba | 隐藏状态更新中的偏置项 |
| b y b_y by | 输出层的偏置项 |
| tanh ( ⋅ ) \tanh(\cdot) tanh(⋅) | 隐藏层激活函数(亦可记为 g 1 g_1 g1) |
| g 2 ( ⋅ ) g_2(\cdot) g2(⋅) | 输出层激活函数,例如 softmax(分类)或 sigmoid(二分类) |
| L ⟨ t ⟩ L^{\langle t \rangle} L⟨t⟩ | 第 t t t 个时间步的损失(如交叉熵) |
| L L L | 整个序列的总损失, L = ∑ t = 1 T y L ⟨ t ⟩ L = \sum_{t=1}^{T_y} L^{\langle t \rangle} L=∑t=1TyL⟨t⟩ |
| $\frac{\partial L}{\partial b_y} | 损失对输出偏置 b y b_y by 的梯度 |
| ∂ L ∂ a ⟨ k ⟩ \frac{\partial L}{\partial a^{\langle k \rangle}} ∂a⟨k⟩∂L | 损失对第 k k k 个时间步隐藏状态的梯度 |
| diag ( g 1 ′ ( a ⟨ k ⟩ ) ) \operatorname{diag}(g_1'(a^{\langle k \rangle})) diag(g1′(a⟨k⟩)) | 由 g 1 g_1 g1 在 a ⟨ k ⟩ a^{\langle k \rangle} a⟨k⟩ 处的导数组成的对角矩阵 |
| ∂ a ⟨ k ⟩ ∂ a ⟨ k − 1 ⟩ \frac{\partial a^{\langle k \rangle}}{\partial a^{\langle k-1 \rangle}} ∂a⟨k−1⟩∂a⟨k⟩ | 隐藏状态对前一隐藏状态的雅可比矩阵 |
| T y T_y Ty | 输出序列的长度(时间步总数) |
1.前向传播forward
隐藏状态:
a ⟨ t ⟩ = tanh ( ( W a x W a a ) ( x ⟨ t ⟩ a ⟨ t − 1 ⟩ ) + b a ) = tanh ( W a x x ⟨ t ⟩ + W a a a ⟨ t − 1 ⟩ + b a ) \begin{align*} a^{\langle t \rangle} &= \tanh\left( \begin{pmatrix} W_{ax} & W_{aa} \end{pmatrix} \begin{pmatrix} x^{\langle t \rangle} \\ a^{\langle t-1 \rangle} \end{pmatrix} + b_a \right) \\ &= \tanh( W_{ax} x^{\langle t \rangle} + W_{aa} a^{\langle t-1 \rangle} + b_a ) \end{align*} a⟨t⟩=tanh((WaxWaa)(x⟨t⟩a⟨t−1⟩)+ba)=tanh(Waxx⟨t⟩+Waaa⟨t−1⟩+ba)
输出:
y ^ ⟨ t ⟩ = g 2 ( W y a a ⟨ t ⟩ + b y ) \hat{y}^{\langle t \rangle} = g_2( W_{ya} a^{\langle t \rangle} + b_y ) y^⟨t⟩=g2(Wyaa⟨t⟩+by)
单个时间步的损失:
L ⟨ t ⟩ = CrossEntropy ( y ^ ⟨ t ⟩ , y ⟨ t ⟩ ) L^{\langle t \rangle} = \text{CrossEntropy}( \hat{y}^{\langle t \rangle}, y^{\langle t \rangle} ) L⟨t⟩=CrossEntropy(y^⟨t⟩,y⟨t⟩)
整个序列的总损失:
L = ∑ t = 1 T y L ⟨ t ⟩ L = \sum_{t=1}^{T_y} L^{\langle t \rangle} L=t=1∑TyL⟨t⟩
单个时间步的损失函数: L ⟨ t ⟩ ( y ^ ⟨ t ⟩ , y ⟨ t ⟩ ) \mathcal{L}^{\langle t \rangle}(\hat{y}^{\langle t \rangle}, y^{\langle t \rangle}) L⟨t⟩(y^⟨t⟩,y⟨t⟩)
(这是一个函数)
在时间步t的损失(标量): L ⟨ t ⟩ = L ⟨ t ⟩ ( y ^ ⟨ t ⟩ , y ⟨ t ⟩ ) L^{\langle t \rangle} = \mathcal{L}^{\langle t \rangle}(\hat{y}^{\langle t \rangle}, y^{\langle t \rangle}) L⟨t⟩=L⟨t⟩(y^⟨t⟩,y⟨t⟩)
(这是一个具体的数值)
2.反向传播
损失函数:
L ⟨ t ⟩ ( y ^ ⟨ t ⟩ , y ⟨ t ⟩ ) = − y ⟨ t ⟩ log y ^ ⟨ t ⟩ − ( 1 − y ⟨ t ⟩ ) log ( 1 − y ^ ⟨ t ⟩ ) L ( y ^ , y ) = ∑ t = 1 T y L ⟨ t ⟩ ( y ^ ⟨ t ⟩ , y ⟨ t ⟩ ) \begin{align*} \mathcal{L}^{\langle t \rangle}(\hat{y}^{\langle t \rangle}, y^{\langle t \rangle}) &= -y^{\langle t \rangle} \log \hat{y}^{\langle t \rangle} - (1 - y^{\langle t \rangle}) \log (1 - \hat{y}^{\langle t \rangle}) \\ L(\hat{y}, y) &= \sum_{t=1}^{T_y} \mathcal{L}^{\langle t \rangle}(\hat{y}^{\langle t \rangle}, y^{\langle t \rangle}) \end{align*} L⟨t⟩(y^⟨t⟩,y⟨t⟩)L(y^,y)=−y⟨t⟩logy^⟨t⟩−(1−y⟨t⟩)log(1−y^⟨t⟩)=t=1∑TyL⟨t⟩(y^⟨t⟩,y⟨t⟩)
反向传播(BP梯度):
- 对 b y b_y by 的梯度:
∂ L ∂ b y = ∑ t = 1 T y ( ∂ L ⟨ t ⟩ ∂ y ^ ⟨ t ⟩ ) ( ∂ y ^ ⟨ t ⟩ ∂ b y ) \frac{\partial L}{\partial b_{y}} = \sum_{t=1}^{T_y} \left( \frac{\partial \mathcal{L}^{\langle t \rangle}}{\partial \hat{y}^{\langle t \rangle}} \right) \left( \frac{\partial \hat{y}^{\langle t \rangle}}{\partial b_{y}} \right) ∂by∂L=t=1∑Ty(∂y^⟨t⟩∂L⟨t⟩)(∂by∂y^⟨t⟩)
- 对 a < 1 > a^{<1>} a<1> 的梯度: (链式法则的展开)
∂ L ∂ a ⟨ 1 ⟩ = ∑ t = 1 T y ( ∂ L ⟨ t ⟩ ∂ y ^ ⟨ t ⟩ ) ( ∂ y ^ ⟨ t ⟩ ∂ a ⟨ 1 ⟩ ) = ∑ t = 1 T y ( ∂ L ⟨ t ⟩ ∂ y ^ ⟨ t ⟩ ) ( ∂ y ^ ⟨ t ⟩ ∂ a ⟨ t ⟩ ) ( ∂ a ⟨ t ⟩ ∂ a ⟨ t − 1 ⟩ ) ⋯ ( ∂ a ⟨ 2 ⟩ ∂ a ⟨ 1 ⟩ ) \begin{align*} \frac{\partial L}{\partial a^{\langle 1 \rangle}} &= \sum_{t=1}^{T_y} \left( \frac{\partial \mathcal{L}^{\langle t \rangle}}{\partial \hat{y}^{\langle t \rangle}} \right) \left( \frac{\partial \hat{y}^{\langle t \rangle}}{\partial a^{\langle 1 \rangle}} \right) \\ &= \sum_{t=1}^{T_y} \left( \frac{\partial \mathcal{L}^{\langle t \rangle}}{\partial \hat{y}^{\langle t \rangle}} \right) \left( \frac{\partial \hat{y}^{\langle t \rangle}}{\partial a^{\langle t \rangle}} \right) \textcolor{emphasis}{ \left( \frac{\partial a^{\langle t \rangle}}{\partial a^{\langle t-1 \rangle}} \right) \cdots \left( \frac{\partial a^{\langle 2 \rangle}}{\partial a^{\langle 1 \rangle}} \right) } \end{align*} ∂a⟨1⟩∂L=t=1∑Ty(∂y^⟨t⟩∂L⟨t⟩)(∂a⟨1⟩∂y^⟨t⟩)=t=1∑Ty(∂y^⟨t⟩∂L⟨t⟩)(∂a⟨t⟩∂y^⟨t⟩)(∂a⟨t−1⟩∂a⟨t⟩)⋯(∂a⟨1⟩∂a⟨2⟩)
- 普遍: 对 a < k > a^{<k>} a<k> 的梯度:
∂ L ∂ a ⟨ k ⟩ = ∑ t = k T y ( ∂ L ⟨ t ⟩ ∂ y ^ ⟨ t ⟩ ) ( ∂ y ^ ⟨ t ⟩ ∂ a ⟨ t ⟩ ) ( ∂ a ⟨ t ⟩ ∂ a ⟨ t − 1 ⟩ ) ⋯ ( ∂ a ⟨ k + 1 ⟩ ∂ a ⟨ k ⟩ ) \begin{align*} \frac{\partial L}{\partial a^{\langle k \rangle}} &= \sum_{t=k}^{T_y} \left( \frac{\partial \mathcal{L}^{\langle t \rangle}}{\partial \hat{y}^{\langle t \rangle}} \right) \left( \frac{\partial \hat{y}^{\langle t \rangle}}{\partial a^{\langle t \rangle}} \right) \textcolor{emphasis}{ \left( \frac{\partial a^{\langle t \rangle}}{\partial a^{\langle t-1 \rangle}} \right) \cdots \left( \frac{\partial a^{\langle k+1 \rangle}}{\partial a^{\langle k \rangle}} \right) } \end{align*} ∂a⟨k⟩∂L=t=k∑Ty(∂y^⟨t⟩∂L⟨t⟩)(∂a⟨t⟩∂y^⟨t⟩)(∂a⟨t−1⟩∂a⟨t⟩)⋯(∂a⟨k⟩∂a⟨k+1⟩)
3.梯度消失
∂ L ∂ a ⟨ 1 ⟩ = ∑ t = 1 T y ( ∂ L ⟨ t ⟩ ∂ y ^ ⟨ t ⟩ ) ( ∂ y ^ ⟨ t ⟩ ∂ a ⟨ 1 ⟩ ) = ∑ t = 1 T y ( ∂ L ⟨ t ⟩ ∂ y ^ ⟨ t ⟩ ) ( ∂ y ^ ⟨ t ⟩ ∂ a ⟨ t ⟩ ) ( ∂ a ⟨ t ⟩ ∂ a ⟨ t − 1 ⟩ ) ⋯ ( ∂ a ⟨ 2 ⟩ ∂ a ⟨ 1 ⟩ ) = ∑ t = 1 T y ( ( ∂ L ⟨ t ⟩ ∂ y ^ ⟨ t ⟩ ) × W y a × diag ( g 2 ′ ( a ⟨ t ⟩ ) ) × W a a × diag ( g 1 ′ ( a ⟨ t − 1 ⟩ ) ) × W a a × diag ( g 1 ′ ( a ⟨ t − 2 ⟩ ) ) × ⋯ × W a a × diag ( g 1 ′ ( a ⟨ 1 ⟩ ) ) ⏟ 包含 ( t − 1 ) 个 W a a 的连乘项 ) \begin{align*} \frac{\partial L}{\partial a^{\langle 1 \rangle}} &= \sum_{t=1}^{T_{y}} \left( \frac{\partial L^{\langle t \rangle}}{\partial \hat{y}^{\langle t \rangle}} \right) \left( \frac{\partial \hat{y}^{\langle t \rangle}}{\partial a^{\langle 1 \rangle}} \right) \\ &= \sum_{t=1}^{T_{y}} \left( \frac{\partial L^{\langle t \rangle}}{\partial \hat{y}^{\langle t \rangle}} \right) \left( \frac{\partial \hat{y}^{\langle t \rangle}}{\partial a^{\langle t \rangle}} \right) \left( \frac{\partial a^{\langle t \rangle}}{\partial a^{\langle t-1 \rangle}} \right) \cdots \left( \frac{\partial a^{\langle 2 \rangle}}{\partial a^{\langle 1 \rangle}} \right) \\ &= \sum_{t=1}^{T_{y}} \Bigg( \left( \frac{\partial L^{\langle t \rangle}}{\partial \hat{y}^{\langle t \rangle}} \right) \times W_{ya} \times \text{diag}\left( g_2' ( a^{\langle t \rangle} ) \right) \\ &\quad \times \underbrace{W_{aa} \times \text{diag}\left( g_1' ( a^{\langle t-1 \rangle} ) \right) \times W_{aa} \times \text{diag}\left( g_1' ( a^{\langle t-2 \rangle} ) \right) \times \cdots \times W_{aa} \times \text{diag}\left( g_1' ( a^{\langle 1 \rangle} ) \right)}{\text{包含 } (t-1) \text{ 个 } W{aa} \text{ 的连乘项} } \Bigg) \end{align*} ∂a⟨1⟩∂L=t=1∑Ty(∂y^⟨t⟩∂L⟨t⟩)(∂a⟨1⟩∂y^⟨t⟩)=t=1∑Ty(∂y^⟨t⟩∂L⟨t⟩)(∂a⟨t⟩∂y^⟨t⟩)(∂a⟨t−1⟩∂a⟨t⟩)⋯(∂a⟨1⟩∂a⟨2⟩)=t=1∑Ty((∂y^⟨t⟩∂L⟨t⟩)×Wya×diag(g2′(a⟨t⟩))×包含 (t−1) 个 Waa 的连乘项 Waa×diag(g1′(a⟨t−1⟩))×Waa×diag(g1′(a⟨t−2⟩))×⋯×Waa×diag(g1′(a⟨1⟩)))
梯度 ∂ L ∂ a ⟨ 1 ⟩ \frac{\partial L}{\partial a^{\langle 1 \rangle}} ∂a⟨1⟩∂L 的大小强烈依赖于权重矩阵 W a a W_{aa} Waa 的连乘:
W a a ∼ small → Vanishing (梯度消失) W a a ∼ large → Exploding (梯度爆炸) \begin{align*} W_{aa} &\sim \text{small} \rightarrow \text{Vanishing} \quad \text{(梯度消失)} \\ W_{aa} &\sim \text{large} \rightarrow \text{Exploding} \quad \text{(梯度爆炸)} \end{align*} WaaWaa∼small→Vanishing(梯度消失)∼large→Exploding(梯度爆炸)
梯度从 a ⟨ t ⟩ a^{\langle t \rangle} a⟨t⟩ 传回 a ⟨ 1 ⟩ a^{\langle 1 \rangle} a⟨1⟩,需要连续乘以 t − 1 t-1 t−1 个雅可比矩阵 ∂ a ⟨ k ⟩ ∂ a ⟨ k − 1 ⟩ \dfrac{\partial a^{\langle k \rangle}}{\partial a^{\langle k-1 \rangle}} ∂a⟨k−1⟩∂a⟨k⟩
∂ a ⟨ k ⟩ ∂ a ⟨ k − 1 ⟩ = W a a ⋅ diag ( g 1 ′ ( a ⟨ k − 1 ⟩ ) ) \frac{\partial a^{\langle k \rangle}}{\partial a^{\langle k-1 \rangle}} = W_{aa} \cdot \operatorname{diag}\left(g_{1}^{\prime}\left(a^{\langle k-1 \rangle}\right)\right) ∂a⟨k−1⟩∂a⟨k⟩=Waa⋅diag(g1′(a⟨k−1⟩))
误差曲面:
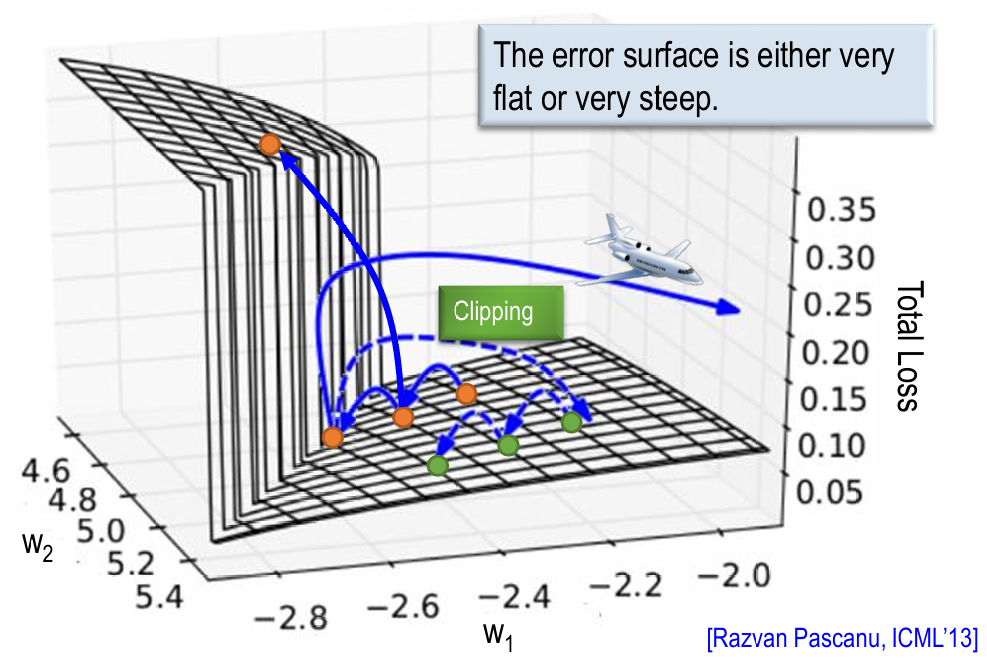
-> 梯度消失问题使得RNN更像是"短时记忆"模型,它更倾向于根据临近的信息做预测,而会"忘记"序列开头的重要信息
LSTM: Long Short-term Memory
与RNN的不同之处
图标说明:

RNN只用了一个tanh, 而lstm有3个sigmoid和1个tanh:
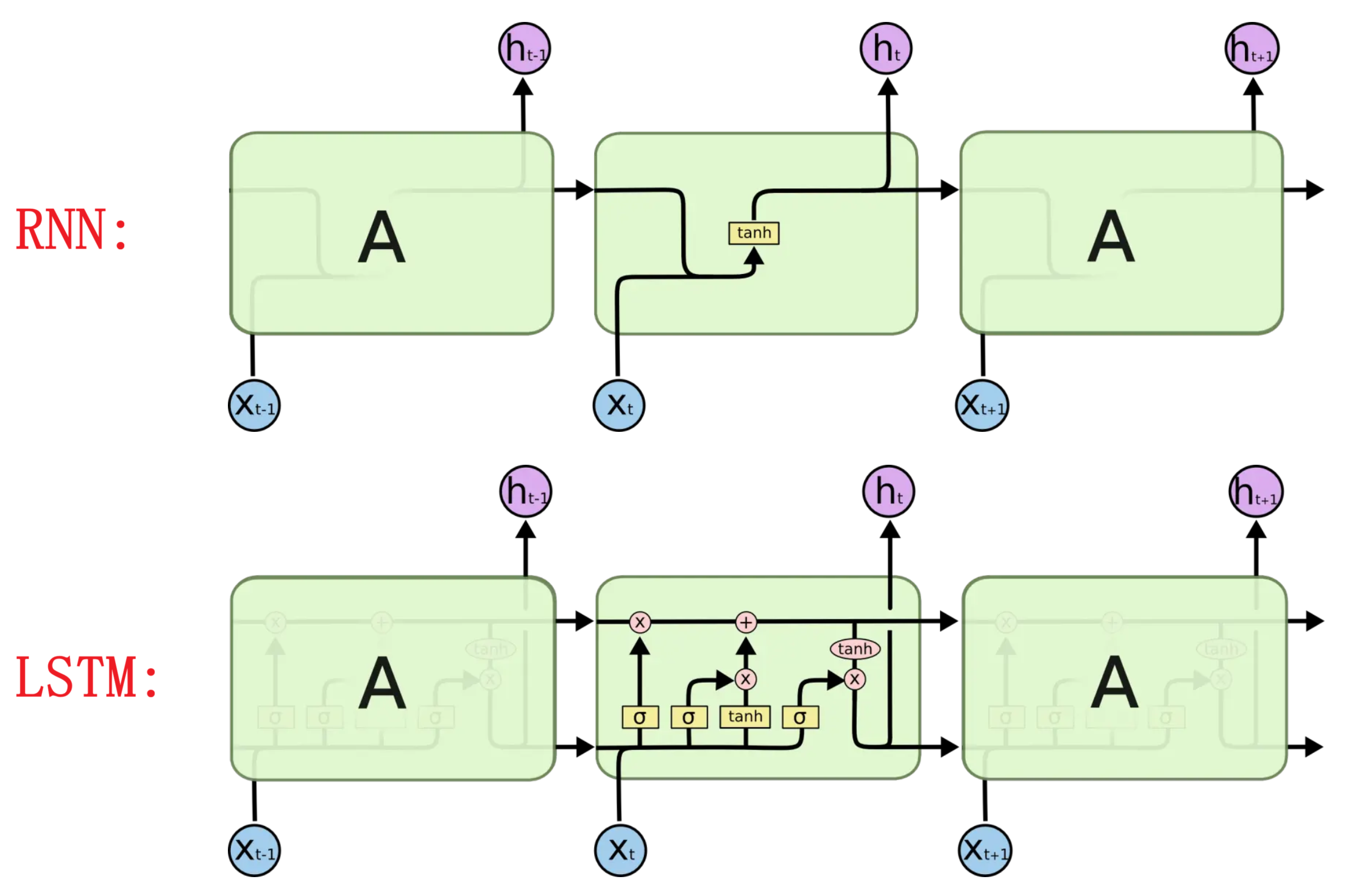
结构拆解
1.细胞状态cell state
直接在整个链上运行,只有一些少量的线性交互(遗忘门的逐元素乘法, 输入门的逐元素加法)
-> 信息在上面流传保持不变会很容易

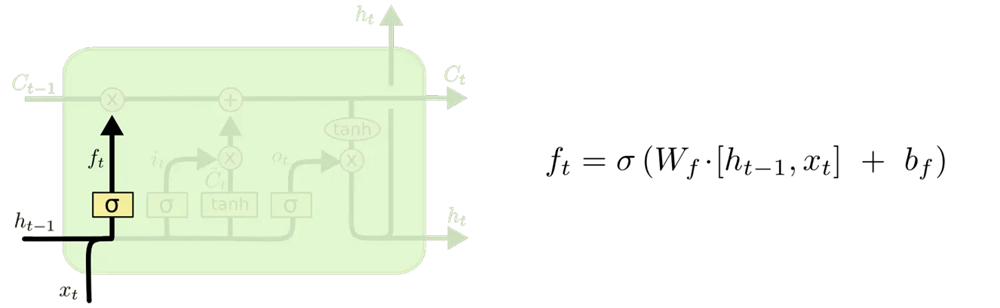
2.遗忘门forget gate
对于每个在细胞状态 C t − 1 C_{t-1} Ct−1中的值
读取 h t − 1 h_{t-1} ht−1和 x t x_t xt,输出一个在 0 到 1 之间的数值代表矩阵的各个元素是否要被记住
-> 后续用于逐元素相乘, 相当于权重
1 表示"完全保留"
0 表示"完全舍弃"
f t = σ ( W h f h t − 1 + W x f x t + b f ) = σ ( W f [ h t − 1 , x t ] + b f ) \begin{align} f_t &=\sigma(W_{hf} h_{t-1}+W_{xf} x_t+b_f) \\ &=\sigma(W_{f} [h_{t-1}, x_t]+b_f) \end{align} ft=σ(Whfht−1+Wxfxt+bf)=σ(Wf[ht−1,xt]+bf)
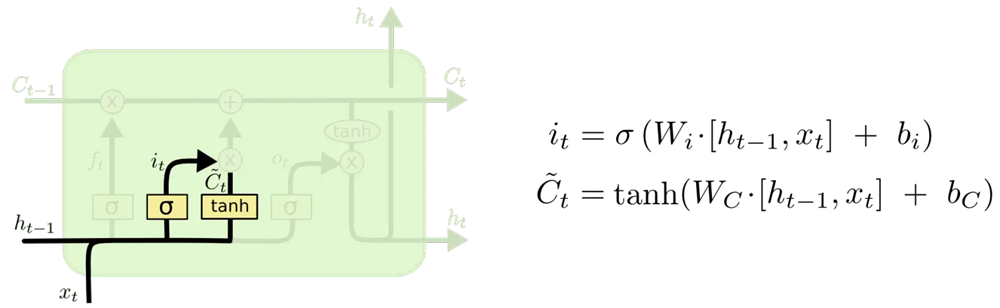
3.输入门input gate
sigmoid 决定什么值将要被纳入细胞状态
tanh 层创建一个新的候选值向量 C ~ t \tilde{C}t C~t,且会被加入到细胞状态中
i t = σ ( W h i h t − 1 + W x i x t + b i ) = σ ( W i [ h t − 1 , x t ] + b i ) C t ~ = t a n h ( W C [ h t − 1 , x t ] + b C ) \begin{align} & i_t=\sigma(W{hi} h_{t-1}+W_{xi} x_t+b_i)=\sigma(W_{i} [h_{t-1}, x_t]+b_i) \\ & \widetilde{C_t}=tanh(W_{C} [h_{t-1}, x_t]+b_C) \end{align} it=σ(Whiht−1+Wxixt+bi)=σ(Wi[ht−1,xt]+bi)Ct =tanh(WC[ht−1,xt]+bC)
4.输出门output gate
sigmoid 来确定细胞状态的哪个部分将输出出去
把细胞状态通过 tanh 进行处理 并将它和 sigmoid的输出 逐点相乘,得到输出的 h t h_t ht
o t = σ ( W h o h t − 1 + W x o x t + b o ) = σ ( W o [ h t − 1 , x t ] + b o ) h t = o t ∗ t a n h ( C t ) \begin{align} & o_t=\sigma(W_{ho} h_{t-1}+W_{xo} x_t+b_o)=\sigma(W_{o} [h_{t-1}, x_t]+b_o) \\ & h_t=o_t*tanh(C_t) \end{align} ot=σ(Whoht−1+Wxoxt+bo)=σ(Wo[ht−1,xt]+bo)ht=ot∗tanh(Ct)
为何这里不用sigmoid而用tanh:
- cell state c t c_t ct 表示的是 "记忆信息",里面不仅有"大小",还有"方向"(正负意义)
- sigmoid 会严重破坏信息方向,而 tanh 保留符号(正/负)信息
- 这种对称性和可正可负,是深度学习中非常重要的性质

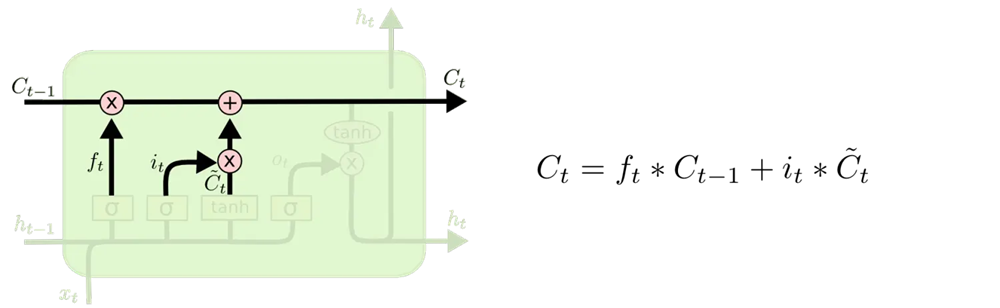
5.更新旧细胞状态 C i − 1 → C i C_{i-1} \rightarrow C_i Ci−1→Ci
把旧状态 C i − 1 C_{i-1} Ci−1与 f t f_t ft逐元素相乘 -> 丢弃掉需要丢弃的信息
接着加上新的候选值 i t ∗ C ~ t i_t * \tilde{C}t it∗C~t -> 记住新的输入
C t = f t ∗ C t − 1 + i t ∗ C t ~ C_t=f_t*C{t-1}+i_t*\widetilde{C_t} Ct=ft∗Ct−1+it∗Ct
更多架构
1.窥视孔LSTM(poophole LSTM)
添加"窥视孔连接" -> 允许门直接读取细胞状态本身
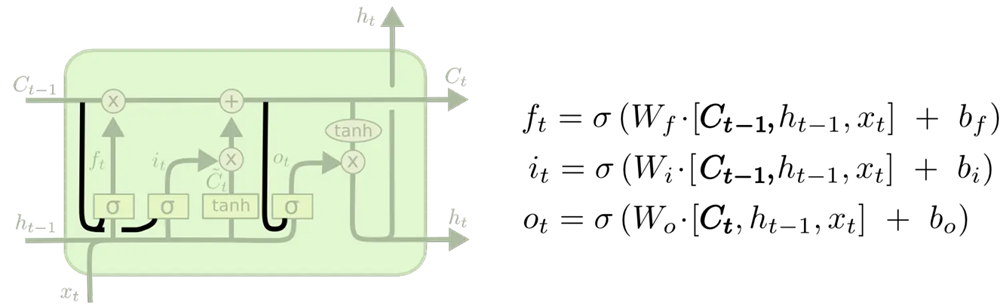
2.耦合(couple)遗忘门与输入门
不再分别决定 要忘记什么以及要向哪些部分添加新信息,而是合并处理
-> 只在要用新内容( f t f_t ft)替换旧内容时, 才进行遗忘( 1 − f t 1-f_t 1−ft)操作
-> 只在遗忘掉某些旧信息时, 才会向细胞状态输入新值
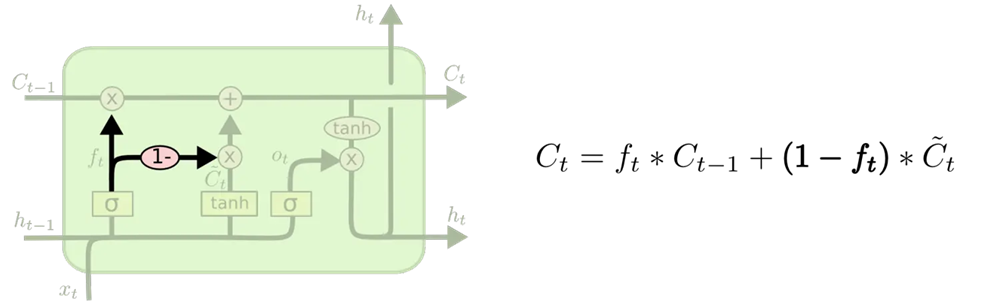
3.门控循环单元GRU(Gated Recurrent Unit)
-
将遗忘门和输入门组合 成一个单一的"更新门"
-
将细胞状态和隐藏状态合并
-> 比标准LSTM更简单,并且日益流行
