数据结构与算法精解：时间序列降采样算法LTOB

前言

本篇博客主要讲解的是时间序列降采样算法LTOB，LTOB全称为Largest-Triangle-One-Bucket，这是一种旨在减少时序数据量同时保留其主要形状特征的方法。本篇博客将对其原理进行讲解，并且附带C++代码示例以及使用QT实现的相关可视化示例(GitHub开源)

LTOB原理

LTOB算法原理：**将时间序列数据划分为若干个大小相同的"桶"，然后在每个桶内选择一个最具代表性的数据点。其选择标准基于最大三角形面积原理，即选择那个与相邻点能形成最大有效面积的点，这样的点通常位于数据变化的关键位置（如波峰、波谷），有助于保留原始序列的整体趋势和关键特征。**具体的算法流程可以参考下图：

图1.LTOB算法流程

在LTOB算法中会将数据点进行均匀的划分到每一个桶内，桶的个数取决于需要降低采样目标，也就是需要把数据降低到多少个点，那么桶就应该为多少个。为了实现均匀的把数据点划分到每一个桶内，就不能使用除法进行计算，因为这样会导致最后得到的数可能不是整数，而LTOB中采用的是累积计数的方法把数据点进行均匀的划分，具体的计算公式如下：

图2.累计计数法

根据累计计数法，我们举个例子。假设有一个数据序列一共有10个数据点(N=10)，而我们需要划分为5个桶(M=5)进行降采样，那么每一个桶的理想容量就是2(M/N)，使用累计计数法进行划分的结果如下：

桶0(i=0)：起始索引为0 * 2 = 0，结束索引为[1 * 2] - 1 = 1，总共包含0和1两个点
桶1(i=1)：起始索引为1 * 2 = 2，结束索引为[2 * 2] - 1 = 3，总共包含2和3两个点
桶2(i=2)：起始索引为2 * 2 = 4，结束索引为[3 * 2] - 1 = 5，总共包含4和5两个点
桶3(i=3)：起始索引为3 * 2 = 6，结束索引为[4 * 2] - 1 = 7，总共包含6和7两个点
桶4(i=4)：起始索引为4 * 2 = 8，结束索引为[5 * 2] - 1 = 9，总共包含8和9两个点

这是划分5个桶的情况，即划分为奇数桶的情况，接下来我们假设划分的桶为4个(M=4)进行降采样，那么每一个桶的理想容量就是2.5(M/N)，由于存在小数所以会使用向下取整的方式进行转换，而使用累计计数法进行划分的结果如下：

桶0(i=0)：起始索引为0 * 2.5 = 0，结束索引为[1 * 2.5] - 1 = 1.5 = 1，总共包含0和1两个点
桶1(i=1)：起始索引为1 * 2.5 = 2.5 = 2，结束索引为[2 * 2.5] - 1 = 4，总共包含2，3和4三个点
桶2(i=2)：起始索引为2 * 2.5 = 5，结束索引为[3 * 2.5] - 1 = 7.5 = 6，总共包含5和6两个点
桶3(i=3)：起始索引为3 * 2.5 = 7.5 = 7，结束索引为[4 * 2.5] - 1 = 9，总共包含7，8和9三个点

不同的划分方式都可以将数据点妥善分配到各个桶中，并且没有数据点没有遗漏，为了更好的展示划分的结果，可以参考下图：

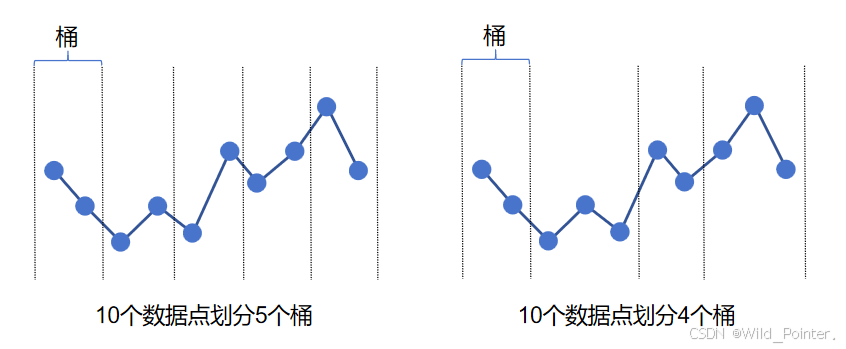
图3.桶的划分

当我们划分完桶以后，我们发现并不是所有桶中的点都能组成三角形的，所以我们不能在这些桶内计算其三角形的面积，要想计算其三角形的面积就必须得跨桶计算。并且我们发现大多数情况下第一个桶和最后一个桶要计算其三角形面积确定其点的面积是很难的，所以我们需要确定LTOB算法中的边界条件，即把第一个桶的代表点看作数据序列中的第一个点，最后一个桶的代表点看作数据序列中的最后一个点，而剩下的桶则进行跨桶来组成三角形计算其面积。具体可以参考下图：

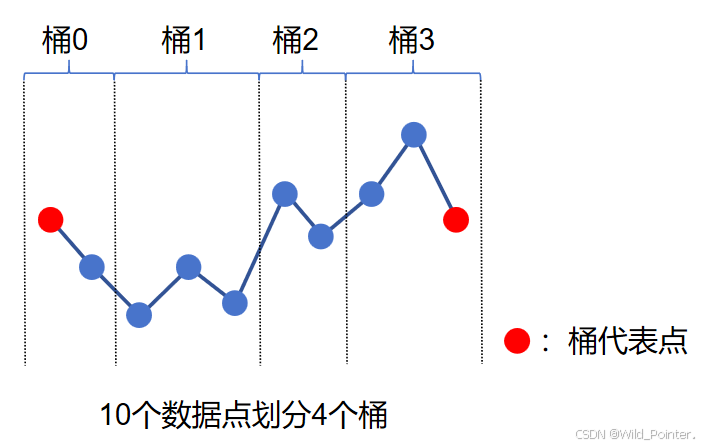
图4.LTOB算法中的边界划分

当我们清楚了边界条件以后，我们需要计算剩余的桶中的代表点。而为了组成三角形并计算面积，桶中的每一个数据点都需要进行跨桶计算，即当前的数据点要以上一个桶的代表点和下一个桶的平均值点组成三角形计算其面积。即LOTB算法中组成三角形(A,B,C)的核心逻辑如下：
1.顶点A(前一个锚点)：上一个桶的代表点

2.顶点B(当前计算点)：当前桶内计算的数据点

3.顶点C(后一个锚点)：下一个桶中所有数据点的平均值

为了更好的了解LOTB算法中组成三角形的核心逻辑，读者可以参考下图：

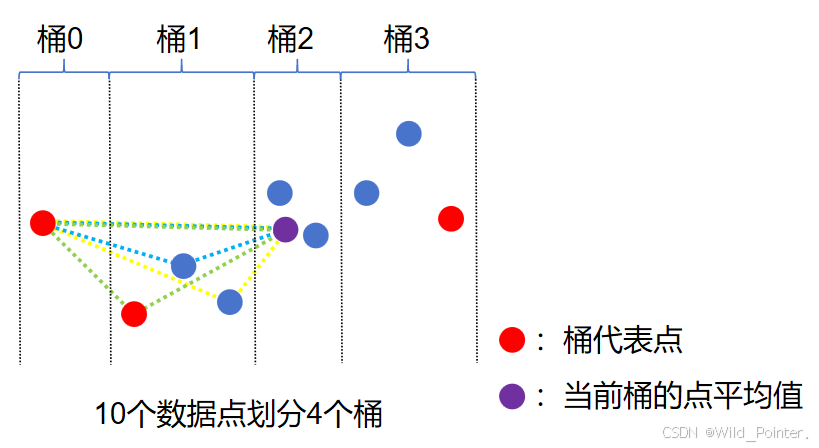
图5.LOTB算法中三角形面积的计算

通过计算每一个桶的代表点，我们就可以筛选掉部分点，从而实现降采样

LTOB优缺点

通过LTOB原理我们可以发现其优缺点，具体如下：
1.LTOB的优点：能够有效的保留时间序列的总体形状和关键特征，其计算复杂度相对于一些更复杂的算法（如后续要讲解的LTTB）要低，实现也相对简单。

2.LTOB的缺点：在决策时主要依赖当前桶内的信息，这可能会导致其对全局趋势的把握不如考虑前后关联的更高级算法（如LTTB），也被大家认为是短视的。

LTOB实现

以下是根据原理编写的C++版的LTOB实现代码

cpp 复制代码

/*
*   @brief 计算三角形面积
*   @param[in] ax：顶点A的X轴坐标
*   @param[in] ay：顶点A的Y轴坐标
*   @param[in] bx：顶点B的X轴坐标
*   @param[in] by：顶点B的Y轴坐标
*   @param[in] cx：顶点C的X轴坐标
*   @param[in] cy：顶点C的Y轴坐标
*/
static inline double triArea(double ax, double ay, double bx, double by, double cx, double cy)
{
    return std::abs((ax - cx) * (by - ay) - (ax - bx) * (cy - ay));
}

/*
*   @brief LTOB时间序列降采样算法
*   @param[in] xIn：输入的X轴数据
*   @param[in] yIn：输入的Y轴数据
*   @param[out] xOut：输出的X轴数据
*   @param[out] yOut：输出的Y轴数据
*   @param[in] targetCount：目标点数
*/
void ltobDownsample(const QVector<double>& xIn, const QVector<double>& yIn,
                    QVector<double>& xOut, QVector<double>& yOut, int targetCount)
{
    xOut.clear();
    yOut.clear();

    const int n = xIn.size();   // 输入数据大小
    if (n == 0 || targetCount <= 0) {   // 空数据或目标数量非法直接返回
        return;
    }
    if (targetCount >= n) {         // 不需要降采样：直接返回原始数据
        xOut = xIn;
        yOut = yIn;
        return;
    }
    if (targetCount == 1) {        // 只取首个点
        xOut.push_back(xIn.front());
        yOut.push_back(yIn.front());
        return;
    }

    xOut.reserve(targetCount);
    yOut.reserve(targetCount);

    // 保留第一个点
    xOut.push_back(xIn[0]);
    yOut.push_back(yIn[0]);

    int a = 0; // 上一个已选点的索引
    const double bucketSize = double(n - 2) / double(targetCount - 2);
    for (int i = 0; i < targetCount - 2; ++i) {
        const int bucketStart = int(std::floor(1 + i * bucketSize));
        const int bucketEnd = int(std::floor(1 + (i + 1) * bucketSize));

        // 计算下一桶的均值点（用于与候选点构成三角形）
        double avgX = 0.0, avgY = 0.0;
        int avgStart = int(std::floor(1 + (i + 1) * bucketSize));
        int avgEnd = int(std::floor(1 + (i + 2) * bucketSize));
        if (avgEnd > n - 1) {
            avgEnd = n - 1;
        }
        int avgCount = std::max(1, avgEnd - avgStart);
        for (int k = avgStart; k < avgEnd; ++k) {
            avgX += xIn[k];
            avgY += yIn[k];
        }
        avgX /= avgCount;
        avgY /= avgCount;

        // 在当前桶中选择面积最大的候选点
        double maxArea = -1.0;
        int chosen = bucketStart;
        int bEnd = std::max(bucketStart + 1, bucketEnd);
        for (int j = bucketStart; j < bEnd; ++j) {
            double area = triArea(xIn[a], yIn[a], xIn[j], yIn[j], avgX, avgY);
            if (area > maxArea) {
                maxArea = area;
                chosen = j;
            }
        }
        xOut.push_back(xIn[chosen]);
        yOut.push_back(yIn[chosen]);
        a = chosen;
    }

    // 保留最后一个点
    xOut.push_back(xIn[n - 1]);
    yOut.push_back(yIn[n - 1]);
}

LTOB示例开源

GitHub开源链接如下：LTOBDemohttps://github.com/3020Xmy/LTOBDemo

数据结构与算法精解：时间序列降采样算法LTOB

目录

前言

相关参考

LTOB原理

LTOB优缺点

LTOB实现

LTOB示例开源