力扣：2050. 并行课程 III

给你一个整数 n ，表示有 n 节课，课程编号从 1 到 n 。同时给你一个二维整数数组 relations ，其中 relations[j] = [prevCoursej, nextCoursej] ，表示课程 prevCoursej 必须在课程 nextCoursej 之前完成（先修课的关系）。同时给你一个下标从 0 开始的整数数组 time ，其中 time[i] 表示完成第 (i+1) 门课程需要花费的月份数。

请你根据以下规则算出完成所有课程所需要的最少月份数：

如果一门课的所有先修课都已经完成，你可以在任意时间开始这门课程。
你可以同时上 任意门课程 。

请你返回完成所有课程所需要的最少月份数。

**注意：**测试数据保证一定可以完成所有课程（也就是先修课的关系构成一个有向无环图）。

示例 1:

复制代码

输入：n = 3, relations = [[1,3],[2,3]], time = [3,2,5]
输出：8
解释：上图展示了输入数据所表示的先修关系图，以及完成每门课程需要花费的时间。
你可以在月份 0 同时开始课程 1 和 2 。
课程 1 花费 3 个月，课程 2 花费 2 个月。
所以，最早开始课程 3 的时间是月份 3 ，完成所有课程所需时间为 3 + 5 = 8 个月。

示例 2：

复制代码

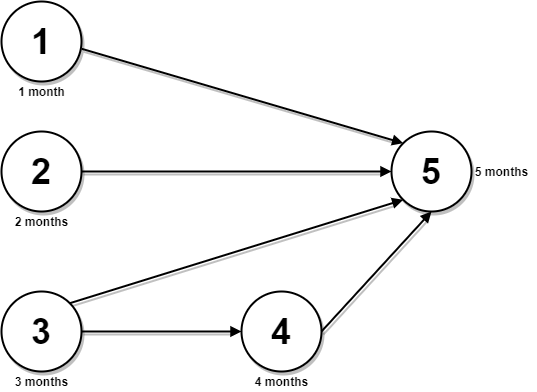
输入：n = 5, relations = [[1,5],[2,5],[3,5],[3,4],[4,5]], time = [1,2,3,4,5]
输出：12
解释：上图展示了输入数据所表示的先修关系图，以及完成每门课程需要花费的时间。
你可以在月份 0 同时开始课程 1 ，2 和 3 。
在月份 1，2 和 3 分别完成这三门课程。
课程 4 需在课程 3 之后开始，也就是 3 个月后。课程 4 在 3 + 4 = 7 月完成。
课程 5 需在课程 1，2，3 和 4 之后开始，也就是在 max(1,2,3,7) = 7 月开始。
所以完成所有课程所需的最少时间为 7 + 5 = 12 个月。

提示：

1 <= n <= 5 * 104
0 <= relations.length <= min(n * (n - 1) / 2, 5 * 104)
relations[j].length == 2
1 <= prevCoursej, nextCoursej <= n
prevCoursej != nextCoursej
所有的先修课程对 [prevCoursej, nextCoursej] 都是 互不相同 的。
time.length == n
1 <= time[i] <= 104
先修课程图是一个有向无环图。

思路：

首先初始化入度数组indegree统计每门课程（结点）的前置依赖数量，通过大小为5e4 + 10的邻接表a构建课程依赖有向图，同时定义dist数组记录完成每门课程的最早时间；

遍历先修关系数组relations，将 $u, v$ （修 v 需先修 u）转化为从 u 指向 v 的有向边，更新 v 的入度并填充邻接表。

接着筛选出所有入度为 0 的课程，若该课程无后续课程则直接将其学习时长存入数组b，否则加入队列作为排序起点；

随后循环取出队首课程u，若u无后续课程则将其完成时间（dist $u$ + time $u-1$ ）存入b，否则遍历其所有后续课程v，先将v的入度减 1，再更新v的最早完成时间为 "当前值" 与 "u的完成时间 + u的学习时长" 的较大值（保证v在所有先修课完成后开始），若v入度变为 0 则加入队列。

最后对存储所有课程完成时间的数组b排序，取最大值作为完成所有课程的最短时间。

AC代码：

cpp 复制代码

class Solution {
public:
	int minimumTime(int n, vector<vector<int>>& relations, vector<int>& time) {
		vector<int> indegree(n + 1, 0); // 计算入度
		const int N = 5e4 + 10;
		vector<int> a[N]; // 邻接表建图
		vector<int> dist(n + 1, 0);
		for (auto it : relations) {
			int u = it[0];
			int v = it[1];
			indegree[v]++;
			a[u].push_back(v);
		}
		queue<int> q;
		vector<int> b;
		for (int i = 1; i <= n; i++) {
			if (indegree[i] == 0) {
				if (a[i].empty()) {
					b.push_back(time[i - 1]);
				}
				else {
					q.push(i);
				}
				
			}
		}
		while (!q.empty()) {
			int u = q.front();
			q.pop();
			if (a[u].empty()) {
				b.push_back(dist[u] + time[u - 1]);
				continue;
			}

			for (auto v : a[u]) {
				indegree[v]--;
				if (dist[v] < dist[u] + time[u - 1]) {
					dist[v] = dist[u] + time[u - 1];
				}
				if (indegree[v] == 0) {
					q.push(v);
				}
			}
		}
		sort(b.begin(), b.end());
		int ans = b[b.size() - 1];
		return ans;
	}
};