EconML实战：使用DeepIV、DROrthoForest与CausalForestDML进行因果推断详解

本项目旨在详细解释一系列用于因果推断的Python代码实现。内容面向有一定机器学习基础，但对因果推断领域尚不熟悉的读者。我们将深入探讨代码的每个阶段，解释其背后的原理、目的和具体实现细节 。通过本项目，将能够理解这些复杂的因果模型是如何工作的，并具备将其应用于自己数据集的能力。

核心概念：什么是因果推断？

在机器学习中，我们常常关注预测（Prediction）：给定特征X，预测结果Y。例如，根据用户的浏览历史预测他是否会点击广告。

然而，在许多现实场景中，我们更关心干预（Intervention）的效果：如果我们改变某个变量T（Treatment，处理变量），结果Y会如何变化？这就是因果推断的核心问题。

例如：

• 给病人用新药（T=1）相比于用安慰剂（T=0），病人的康复率（Y）会提高多少？

• 实施一项新的教学方法（T=1）相比于传统方法（T=0），学生的考试成绩（Y）会提升多少？

• 调整产品价格（T）会对销售量（Y）产生多大的影响？

挑战：混淆（Confounding）

直接比较接受处理（T=1）和未接受处理（T=0）的群体的结果Y通常是错误的。为什么？

因为决定个体是否接受处理的因素（通常称为混淆变量 W, Confounders）可能同时也会影响结果Y。

• 例如，在药物试验中，如果医生倾向于给病情更严重的病人使用新药，那么即使新药有效，直接比较用药组和未用药组的康复率也可能会低估药效，因为用药组的病人本身就"底子差"。这里的"病情严重程度"就是一个混淆变量W。

因果推断的目标 就是在使用观测数据（而非严格的随机对照试验数据）时，通过各种统计和机器学习方法，剥离混淆变量W的影响，从而估计出处理T对结果Y的真实因果效应。

异质性处理效应 (Heterogeneous Treatment Effects, HTE)

同一个处理（如新药、新政策）对不同个体的影响可能不同。

• 例如，新药可能对年轻人更有效，对老年人效果较差。这种因果效应随个体特征（协变量 X, Covariates/Features）变化的现象称为异质性处理效应。估计HTE对于个性化决策（如精准医疗、个性化营销）至关重要。

本教程将详细介绍几种先进的模型来处理混淆问题并估计（异质性）因果效应。

第一阶段：环境配置与库导入

目的: 准备运行代码所需的环境，导入所有必需的Python库。

讲解: 这一步是任何Python项目的标准起始点。我们导入了：

• warnings

  : 用于控制警告信息的显示，simplefilter('ignore')可以隐藏一些库版本更新或不推荐用法产生的警告，让输出更整洁。

• numpy

  (np): Python中科学计算的基础库，用于高效处理数组和矩阵。

• pandas

  (pd): 提供强大的数据结构（如DataFrame），方便进行数据处理和分析。

• matplotlib.pyplot

  (plt) 和 seaborn (sns): 流行的Python数据可视化库，用于绘制各种图表。

• sklearn

  : Scikit-learn库，包含大量的机器学习算法（如线性模型Lasso、LogisticRegression，聚类KMeans，降维PCA等）和工具。

• keras

  : 一个高级神经网络API，这里用于构建DeepIV模型中的神经网络部分。

• econml

  : 微软开发的因果推断库，包含了本教程核心的多种先进因果模型，如DeepIV, DROrthoForest, CausalForestDML等。这些模型专门设计用来处理混淆问题并估计因果效应。

• 其他辅助库如datetime, time, itertools。

  导入基础库并忽略警告信息import warningswarnings.simplefilter('ignore') # 忽略运行中可能出现的警告信息，保持输出干净import datetimeimport time

  导入数据处理和可视化相关库import numpy as np # 用于数值计算，特别是数组操作from itertools import product # 用于生成笛卡尔积，方便创建测试数据集from sklearn.linear_model import Lasso, LogisticRegression # 导入线性模型：Lasso回归和逻辑回归import matplotlib.pyplot as plt # 用于绘制图表import pandas as pd # 用于数据处理，特别是DataFrame结构

  导入因果推断相关库 (EconML)import econml # 导入EconML主库# 从EconML的orf(Orthogonal Random Forest)模块导入两种基于森林的因果模型from econml.orf import DMLOrthoForest, DROrthoForest# 从EconML的dml(Double Machine Learning)模块导入因果森林模型from econml.dml import CausalForestDML# 从EconML的sklearn扩展中导入带权重的Lasso模型，用于某些因果模型的内部估计from econml.sklearn_extensions.linear_model import WeightedLassoCVWrapper, WeightedLasso

  从EconML的dr(Double Robust)模块导入线性双重稳健学习器 (虽然这里没直接用，但属于常用工具)from econml.dr import LinearDRLearner# 从EconML的iv(Instrumental Variable)的nnet(Neural Network)模块导入DeepIV模型from econml.iv.nnet import DeepIVimport keras # 导入Keras深度学习库，用于构建DeepIV的神经网络部分import matplotlib.pyplot as plt # 再次导入，确保可用

  导入其他辅助库import seaborn as sns # 另一个强大的可视化库，基于matplotlibfrom sklearn.linear_model import LassoCV # 带交叉验证的Lasso模型from sklearn.ensemble import GradientBoostingRegressor # 梯度提升回归模型，可用作内部估计器from econml.inference import BootstrapInference # 用于进行自助法推断（如计算置信区间）

  再次忽略警告 (确保后续代码块也不会有警告干扰)import warningswarnings.simplefilter('ignore')

---

第二阶段：数据生成

目的: 创建一个模拟数据集，其中我们人为设定了真实的因果关系和混淆机制。这使得我们能够评估后续因果模型的效果，因为我们可以将模型估计出的因果效应与我们设定的"真实"效应进行比较。

讲解: 生成模拟数据的步骤如下：

1. 定义真实处理效应函数 (exp_te)

   : 我们设定真实的个体处理效应（Treatment Effect, TE）仅依赖于协变量X的第一个维度x[0]，具体形式为 exp(2*x[0])。这意味着处理效应是异质性 的，随着x[0]的增大而指数级增大。

2. 设置参数

   : 定义样本量n、控制变量W的维度n_w、协变量X的维度n_x等。support_size定义了W中实际影响结果Y和处理T的变量数量，引入了稀疏性。

3. 生成变量

   • TE * T

     : 处理的真实因果效应（只有当T=1时才产生影响）。

   • np.dot(W[:, support_Y], coefs_Y)

     : 控制变量W对结果Y的直接影响（混淆路径的一部分）。

   • epsilon_sample(n)

     : 无法观测的随机噪声。 这个生成公式 Y = TE * T + f(W) + error 是因果推断中典型的结果生成模型。

   • W

     (控制变量/混淆变量): 从标准正态分布生成。这些变量会同时影响处理决策T和结果Y，从而产生混淆。

   • X

     (协变量/异质性来源): 从均匀分布生成。这些变量决定了个体处理效应的大小。

   • instrument

     (Z, 工具变量): 从均匀分布生成。这个变量将在DeepIV模型中使用。工具变量需要满足特定条件（与T相关，与Y仅通过T相关），这里我们直接生成一个，假设它满足条件。注意：在真实应用中，找到有效的工具变量是极具挑战性的。

   • TE

     (真实处理效应): 根据上面定义的exp_te函数和生成的X计算每个个体的真实处理效应。

   • T

     (处理变量): 生成一个二元（0或1）处理变量。其生成过程依赖于控制变量 W （np.dot(W[:, support_T], coefs_T)) 和一些随机噪声 eta_sample。通过sigmoid函数将线性组合转换为概率，再用二项分布抽样得到0或1。这种依赖性引入了混淆 ：W高的个体可能更倾向于接受处理（或不接受，取决于系数）。

   • Y

     (结果变量): 结果Y由三部分构成：

4. 生成测试数据 (X_test)

   : 创建一个覆盖X取值范围（这里是0到1）的等间隔数据点网格。我们将用这些点来评估模型估计出的处理效应函数 CATE(x) 的准确性。

   定义处理效应函数 (Ground Truth)def exp_te(x): """ 定义真实的个体处理效应 (Individual Treatment Effect) 这个效应只依赖于协变量X的第一个维度 x[0]。 这是一个指数函数，表示处理效果随 x[0] 增大而增强。 """ return np.exp(2 * x[0])

   设置随机种子和数据集大小参数np.random.seed(1234) # 固定随机种子，使得每次运行结果都一样，方便复现n = 1000 # 生成的样本数量n_w = 30 # 控制变量 W (Confounders / Controls) 的维度support_size = 5 # W 中实际影响 Y 和 T 的变量个数 (引入稀疏性)n_x = 1 # 协变量 X (Heterogeneity source) 的维度

   设置结果变量 Y 的生成参数# 从 W 的 n_w 个维度中，随机选出 support_size 个维度作为真正影响 Y 的变量support_Y = np.random.choice(range(n_w), size=support_size, replace=False)# 为这些影响 Y 的 W 变量生成随机系数 (0到1之间)coefs_Y = np.random.uniform(0, 1, size=support_size)def epsilon_sample(n): """生成结果变量 Y 中的随机噪声项""" return np.random.uniform(-1, 1, size=n)

   设置处理变量 T 的生成参数support_T = support_Y # 在这个模拟中，假设影响 Y 和影响 T 的 W 变量是同一组 (制造混淆)# 为这些影响 T 的 W 变量生成随机系数 (0到1之间)coefs_T = np.random.uniform(0, 1, size=support_size)def eta_sample(n): """生成处理变量 T 决策过程中的随机噪声项""" return np.random.uniform(-1, 1, size=n)

   --- 开始生成核心数据 ---# 生成控制变量 W: n个样本，n_w个特征，服从标准正态分布W = np.random.normal(0, 1, size=(n, n_w))# 生成协变量 X: n个样本，n_x个特征，服从[0, 1]均匀分布X = np.random.uniform(0, 1, size=(n, n_x))# 生成工具变量 Z (Instrumental Variable): n个样本，n_x个特征，服从[0, 1]均匀分布# 假设这个Z满足工具变量的条件 (与T相关，与Y只通过T相关)instrument = np.random.uniform(0, 1, size=(n, n_x))

   生成真实的异质性处理效应 (Heterogeneous Treatment Effect, HTE)# 对每个样本的 X，应用 exp_te 函数计算其真实的 TETE = np.array([exp_te(x_i) for x_i in X])

   生成处理变量 T (二元变量, 0 或 1)# 1. 计算 W 对处理决策的线性影响 + 噪声log_odds = np.dot(W[:, support_T], coefs_T) + eta_sample(n)# 2. 使用 sigmoid 函数将 log-odds 转换为概率 P(T=1 | W)T_sigmoid = 1 / (1 + np.exp(-log_odds))# 3. 根据计算出的概率，为每个样本随机生成 T=1 或 T=0T = np.array([np.random.binomial(1, p) for p in T_sigmoid])# 注意：T 的生成依赖于 W，这是引入混淆的关键步骤

   生成结果变量 Y# Y = (真实的TE * 是否接受处理T) + W对Y的直接影响 + 随机噪声Y = TE * T + np.dot(W[:, support_Y], coefs_Y) + epsilon_sample(n)# 注意：Y 同时受到 T 和 W 的影响

   设置后续模型 (如正交森林) 的参数和测试数据subsample_ratio = 0.4 # 子采样率，森林模型中常用参数# 生成一个测试点集 X_test，覆盖 X 的取值范围 (0到1，步长0.01)# 用于评估模型估计出的处理效应函数 CATE(x)X_test = np.array(list(product(np.arange(0, 1, 0.01), repeat=n_x)))

---

第三阶段：构建和训练DeepIV模型

目的: 使用DeepIV（深度工具变量）模型来估计处理效应。DeepIV特别适用于存在内生性（Endogeneity）问题的情况，即处理变量T与结果模型Y的误差项相关（通常由未观测到的混淆变量引起），并且我们能找到一个有效的工具变量Z。

讲解: DeepIV是一种基于神经网络的两阶段方法：

1. 第一阶段 (Treatment Model):

   • 目的：利用工具变量Z和控制变量W来预测处理变量T的分布 ，而不是仅仅预测T的值。工具变量Z被认为是外生的（不受未观测混淆的影响），它可以帮助我们识别T中那些不受内生性污染的变动。

   • 实现：这里使用一个 Keras 神经网络 treatment_model 来完成。输入是 Z 和 W 的拼接。模型的输出不是直接预测 T，而是被内部用于估计 T 的条件分布（通过混合密度网络或类似技术，DeepIV内部实现）。

2. 第二阶段 (Outcome Model):

   • 目的：基于第一阶段对T分布的估计以及控制变量W来预测结果Y。关键在于，它使用的不是观测到的（可能有内生性的）T，而是利用第一阶段模型从Z和W生成（采样）的、理论上与误差项无关 的T的预测值/分布信息。

   • 实现：使用另一个 Keras 神经网络 outcome_model。输入是采样得到的 T 和 W 的拼接。

3. DeepIV整合与训练:

   • DeepIV

     类将这两个神经网络模型 (m 对应第一阶段，h 对应第二阶段) 结合起来。

   • n_components

     : 用于近似T的条件分布的混合高斯模型（GMM）的组件数。

   • optimizer

     : 指定训练神经网络的优化器（这里用Adagrad）。

   • keras_fit_options

     : 分别为两个阶段的神经网络训练指定参数，如训练轮数(epochs)、验证集比例(validation_split)、早停(EarlyStopping，防止过拟合)。

   • fit(Y, T, X=W, Z=instrument)

     : 使用数据训练整个DeepIV模型。注意这里参数 X 传入的是我们的控制变量 W，而工具变量通过 Z 参数传入。

4. 预测与可视化:

   • 第一张图：将预测值 (cate) 和真实值 (true y) 按预测值大小排序，并计算滚动平均 (rolling(window=15).mean())。这有助于观察预测值和真实值之间的整体趋势关系是否一致，平滑掉个体噪声。

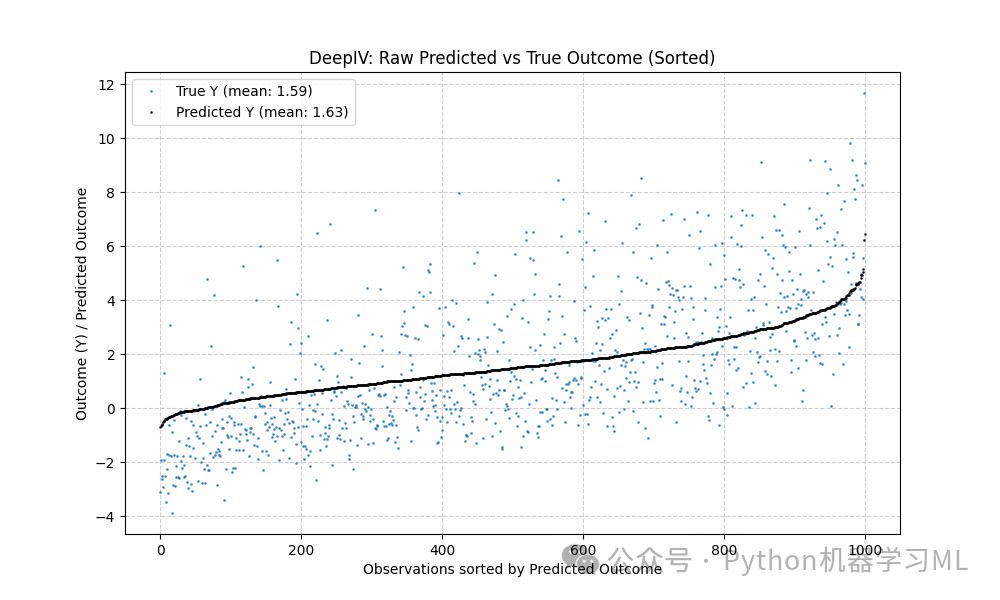
   • 第二张图：直接绘制排序后的原始预测值和真实值，展示更细节的对比。

   • 比较预测值均值和真实值均值。

   • predict(T, W)

     : 使用训练好的模型进行预测。这里预测的是给定 T 和 W 下的期望结果 E[Y|T,W]。由于模型的目标是估计因果效应，这里的预测值可以解释为条件平均处理效应 (Conditional Average Treatment Effect, CATE) 的一种估计。注意：DeepIV的 predict 方法通常用于估计 E[Y|do(T), W] 或相关的量，具体解释可能需要参考EconML文档，但在这里我们将其视为对 Y 的预测，并与真实的 Y 比较。

   • 可视化：代码绘制了两张图。

DeepIV的适用性: 当你怀疑存在未观测的混淆因素，并且能找到一个强而有效的工具变量时，DeepIV是一个强大的选择。但在实践中，找到好的工具变量非常困难。

# --- 构建神经网络模型 ---
# 定义处理模型 (对应 DeepIV 的第一阶段)treatment_model = keras.Sequential([    # 输入层: 维度是 W 的维度 + Z 的维度 (这里 Z 和 X 维度相同，都是 n_x=1)    # 使用 ReLU 激活函数，添加 L2 正则化防止过拟合    keras.layers.Dense(128, activation='relu', input_shape=(n_w + n_x,), # W.shape[1]是n_w, Z的维度是n_x                       kernel_regularizer=keras.regularizers.l2(0.01)),    keras.layers.Dropout(0.17), # Dropout 层，随机失活一部分神经元，增强泛化能力    keras.layers.Dense(64, activation='relu',                       kernel_regularizer=keras.regularizers.l2(0.01)), # 隐藏层 1    keras.layers.Dropout(0.17),    keras.layers.Dense(32, activation='relu',                       kernel_regularizer=keras.regularizers.l2(0.01)), # 隐藏层 2    keras.layers.Dropout(0.17),    keras.layers.Dense(1) # 输出层 (DeepIV内部会处理这个输出来估计T的分布)], name="treatment_model") # 给模型命名
# 定义结果模型 (对应 DeepIV 的第二阶段)outcome_model = keras.Sequential([    # 输入层: 维度是 T 的维度 (1) + W 的维度 (n_w)    keras.layers.Dense(128, activation='relu', input_shape=(1 + n_w,), # T.shape[1]是1 (或没有，默认1), W.shape[1]是n_w                       kernel_regularizer=keras.regularizers.l2(0.01)),    keras.layers.Dropout(0.17),    keras.layers.Dense(64, activation='relu',                       kernel_regularizer=keras.regularizers.l2(0.01)), # 隐藏层 1    keras.layers.Dropout(0.17),    keras.layers.Dense(32, activation='relu',                       kernel_regularizer=keras.regularizers.l2(0.01)), # 隐藏层 2    keras.layers.Dropout(0.17),    keras.layers.Dense(1) # 输出层，预测结果 Y], name="outcome_model") # 给模型命名
# --- 设置训练参数 ---
# 第一阶段 (处理模型) 训练参数keras_fit_options_1 = {    "epochs": 50,                          # 训练轮数    "validation_split": 0.20,              # 从训练数据中分出 20% 作为验证集    # 使用回调函数：EarlyStopping - 如果验证集损失在 2 轮内没有改善，则停止训练，并恢复最佳权重    "callbacks": [keras.callbacks.EarlyStopping(patience=2, restore_best_weights=True)]}# 第二阶段 (结果模型) 训练参数 (这里用了和第一阶段不同的options变量名，但内容相同，可以复用)keras_fit_options_2 = {    "epochs": 50,    "validation_split": 0.20,    "callbacks": [keras.callbacks.EarlyStopping(patience=2, restore_best_weights=True)]}
# --- 创建并训练 DeepIV 模型 ---
# 创建 DeepIV 估计器实例deepIvEst = DeepIV(    n_components=15,  # 混合密度网络 (MDN) 或 GMM 的组件数，用于估计 T 的条件分布    # m: 第一阶段模型函数，接收 Z 和 X (这里是W)，输出 T 的分布参数    # keras.layers.concatenate 用于拼接 Z 和 W 作为输入    m=lambda z, x: treatment_model(keras.layers.concatenate([z, x])),    # h: 第二阶段模型函数，接收 T (采样得到) 和 X (这里是W)，预测 Y    h=lambda t, x: outcome_model(keras.layers.concatenate([t, x])),    n_samples=2,  # 从 T 的条件分布中采样的数量 (较小以加速)    use_upper_bound_loss=True,  # 是否使用特定的损失函数上界 (有时能稳定训练)    n_gradient_samples=0, # 用于梯度计算的样本数 (0表示使用解析梯度，如果可用)    optimizer=keras.optimizers.Adagrad(learning_rate=0.0009),  # 指定优化器和学习率    first_stage_options=keras_fit_options_1,  # 传递第一阶段训练参数    second_stage_options=keras_fit_options_2  # 传递第二阶段训练参数)
# 训练 DeepIV 模型# Y: 结果变量# T: 处理变量# X: 这里传入的是控制变量 W (在DeepIV的语境下，X常指 conditioning set)# Z: 工具变量 instrumentprint("Starting DeepIV training...")deepIvEst.fit(Y=Y, T=T, X=W, Z=instrument)print("DeepIV training finished.")
# --- 预测并可视化结果 ---
# 使用训练好的模型进行预测# 注意：这里的 T 和 W 是原始观测数据y_pred_per = deepIvEst.predict(T, W)print("DeepIV prediction finished.")
# 将预测结果和真实Y放入DataFrame方便处理和绘图te_df_per = pd.DataFrame({'cate': y_pred_per.flatten(), 'true y': Y.flatten()}) # 确保是一维数组
# 按预测的 CATE 值排序te_df_per.sort_values('cate', inplace=True, ascending=True)te_df_per.reset_index(inplace=True, drop=True) # 重置索引
# 计算滚动平均 (窗口大小15)，用于平滑曲线，观察趋势z_per = te_df_per.rolling(window=15, center=True).mean()
# 计算预测值和真实值的均值cate_mean = np.mean(te_df_per['cate'])y_mean = np.mean(te_df_per['true y'])
# --- 绘制第一个图：滚动平均后的 CATE vs True Y ---plt.figure(figsize=(10, 6))plt.plot(z_per['cate'],         marker='.', linestyle='-',         linewidth=0.8, markersize=3,         label=f'Predicted Y (smoothed, mean: {cate_mean:.2f})') # 使用f-string格式化标签
plt.plot(z_per['true y'],         marker='.', linestyle='-',         linewidth=0.8, markersize=3,         label=f'True Y (smoothed, mean: {y_mean:.2f})')
plt.ylabel('Outcome (Y) / Predicted Outcome')plt.xlabel('Observations sorted by Predicted Outcome')plt.title('DeepIV: Smoothed Predicted vs True Outcome (Sorted)')plt.legend()plt.grid(True, linestyle='--', alpha=0.6)plt.show()
# --- 绘制第二个图：原始（排序后）的 CATE vs True Y ---plt.figure(figsize=(10, 6))# 先画 True Yplt.plot(te_df_per['true y'],         marker='.', linestyle='', # 只画点，不连线         markersize=2, alpha=0.7,         label=f'True Y (mean: {y_mean:.2f})')# 再画 CATEplt.plot(te_df_per['cate'],         marker='.', linestyle='', # 只画点         markersize=2, alpha=0.7, color='black',         label=f'Predicted Y (mean: {cate_mean:.2f})')
plt.ylabel('Outcome (Y) / Predicted Outcome')plt.xlabel('Observations sorted by Predicted Outcome')plt.title('DeepIV: Raw Predicted vs True Outcome (Sorted)')plt.legend()plt.grid(True, linestyle='--', alpha=0.6)plt.show()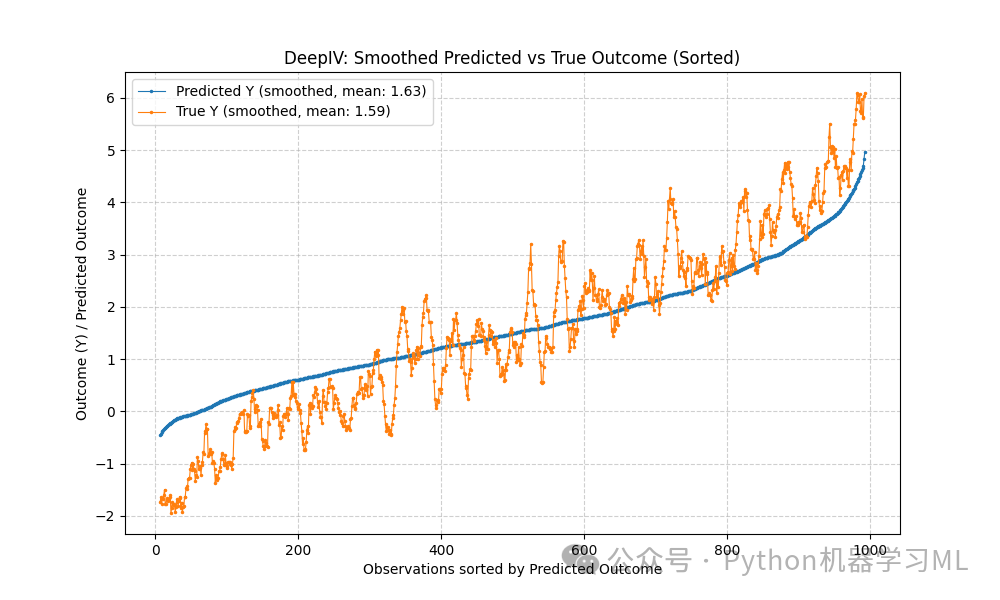

---

第四阶段：DROrthoForest和CausalForestDML进行因果推断

目的: 使用基于双重机器学习 (Double Machine Learning, DML) 和随机森林 思想的先进模型来估计异质性处理效应 (HTE)。这些方法通常对混淆有较好的鲁棒性，并且不需要工具变量（尽管它们可以结合使用）。

讲解:

双重机器学习 (DML) 的核心思想: DML 旨在减少估计因果效应时的偏差，这种偏差可能源于使用复杂机器学习模型来拟合所谓的"讨厌的"参数（nuisance parameters），即结果模型 E[Y|X, W] 和倾向得分模型 P(T=1|X, W)。DML 通过以下步骤实现：

1. 交叉拟合 (Cross-fitting):

   将数据分成几折（例如K折）。

2. 拟合讨厌模型:

   对每一折 i，使用其他 K-1 折的数据训练结果模型和倾向得分模型。

3. 计算残差:

   使用在其他数据上训练好的模型，在第 i 折上计算残差 。结果残差大致为 Y - E[Y|X, W]，处理残差大致为 T - P(T=1|X, W)。

4. 最终阶段估计:

   在所有折的残差上，使用一个相对简单的模型（如岭回归、Lasso或另一个森林）来估计处理残差对结果残差的影响。这个影响就是我们想要的 CATE。 这种交叉拟合的方式确保了用于计算残差的模型没有在当前数据点上"偷看"结果，从而减少了过拟合偏差，并使得理论性质更好（如半参数有效性）。

本节使用的模型:

1. DROrthoForest (Double Robust Orthogonal Random Forest):

   • n_trees

     , min_leaf_size, max_depth, subsample_ratio: 标准的随机森林参数。

   • propensity_model

     : 用于估计倾向得分 P(T=1|X, W) 的模型（这里用带L1惩罚的逻辑回归）。

   • model_Y

     : 用于估计结果模型 E[Y|X, W] 的模型（这里用Lasso）。

   • propensity_model_final

     , model_Y_final: DML最后阶段用于估计CATE的模型（这里用带权重的Lasso）。

   • fit(Y, T, X=X, W=W)

     : 训练模型。注意这里 X 是异质性来源，W 是控制变量。

   • effect(X_test)

     : 估计在测试点 X_test 上的 CATE。

   • effect_interval(X_test)

     : 计算 CATE 的置信区间（通常使用自助法 Bootstrapping of Little Bags, BLB）。

   • 结合了 DML、正交随机森林（Orthogonal Random Forest）和双重稳健性（Double Robustness）的思想。

   • 正交化

     ：旨在使处理效应的估计对讨厌模型的微小误差不敏感。

   • 双重稳健性

     ：意味着只要结果模型 或 倾向得分模型中至少有一个被正确设定（或估计得足够好），那么处理效应的估计就是一致的（渐近无偏）。这是一个非常好的性质。

2. CausalForestDML (Causal Forest Double Machine Learning):

   • model_y

     , model_t: 分别指定内部用于结果模型和处理（倾向得分）模型的估计器（这里用Lasso和逻辑回归）。

   • n_estimators

     , min_samples_leaf, max_depth, max_samples: 森林的参数。

   • discrete_treatment=True

     : 指明处理变量是离散的（0/1）。

   • fit(Y, T, X=X, W=W)

     : 训练。

   • effect(X_test)

     , effect_interval(X_test): 功能同上。

   • summary()

     : 提供模型的摘要信息，可能包括平均处理效应(ATE)的估计等。

   • 也是基于 DML 和森林的方法，实现上可能略有不同，但目标相似：估计 HTE。

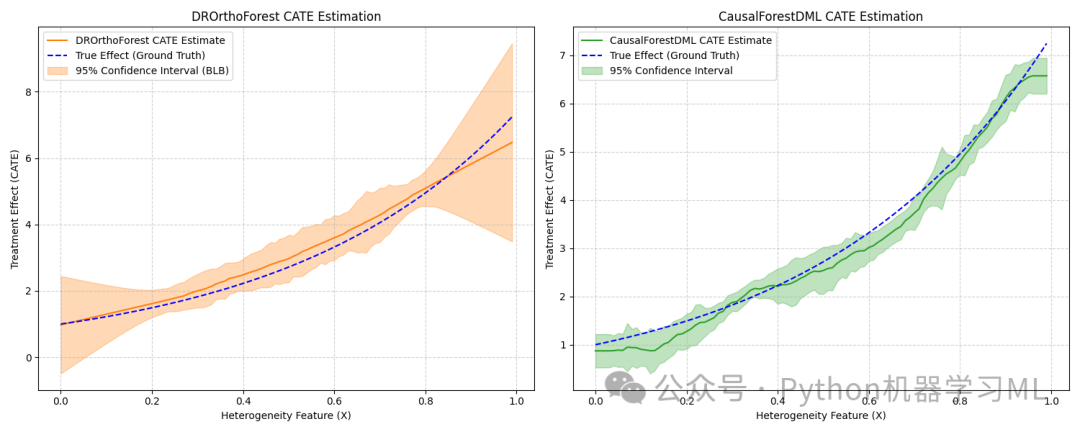
3. 可视化比较:

   • 代码绘制了一个包含两个子图的图形。

   • 左图展示 DROrthoForest 估计的 CATE(x) 曲线、真实的 TE(x) 曲线以及 95% 置信区间。

   • 右图展示 CausalForestDML 的类似结果。

   • 通过比较模型曲线与真实曲线的接近程度以及置信区间的宽度，可以评估模型的性能。

4. 第二个 CausalForestDML 实例与推断:

   • 创建了另一个 CausalForestDML 实例，这次设置了不同的参数（如cv交叉验证折数，discrete_treatment=False虽然我们的T是二元的，但有时设为False也能工作，可能处理方式不同）。

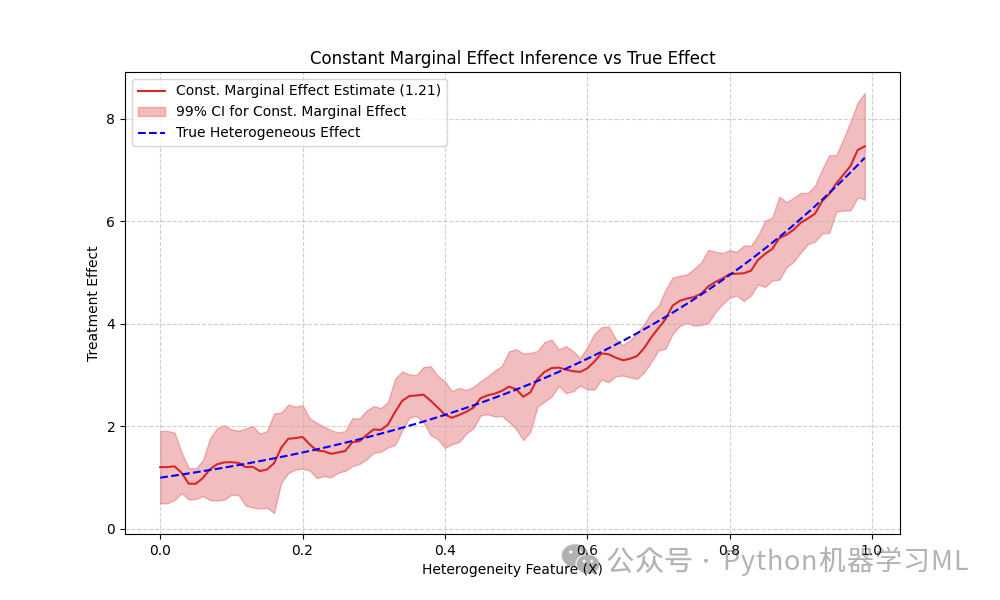
   • const_marginal_effect_inference(X_test)

     : 估计平均边际效应，并进行推断（点估计+置信区间）。这相当于假设效应是恒定的，估计一个平均值。

   • effect_inference(X_test, T0=0, T1=1)

     : 专门估计从 T=0 变化到 T=1 的处理效应，并提供推断（点估计+置信区间）。这对于二元处理变量来说就是估计 CATE。结果被绘制出来。

   • summary_frame()

     : 将推断结果（点估计、标准误、置信区间、p值）以 DataFrame 格式返回。

5. 构建特征矩阵 (total_frame):

   • CATE 的 99% 置信区间下界 (lb)

   • CATE 的 99% 置信区间上界 (ub)

   • CATE 的点估计 (point)

   • 协变量 X

   • 控制变量 W

   • 为了进行后续的聚类分析，代码将以下信息合并到一个 NumPy 数组 total_frame 中：

   • 这个矩阵包含了每个样本的效应估计信息以及它们的特征，是聚类分析的基础。

   --- DROrthoForest ---

   设置子采样率和正则化参数 lambda_regsubsample_ratio = .3# 计算 Lasso 和 Logistic Regression 的 L1 正则化系数 lambda# 这个公式基于理论，目的是平衡模型复杂度和拟合优度，避免过拟合# 它考虑了特征数量 (W.shape[1]) 和样本量 (W.shape[0])lambda_reg = np.sqrt(np.log(W.shape[1]) / (10 * subsample_ratio * W.shape[0]))

   创建 DROrthoForest 估计器实例est = DROrthoForest( n_trees=100, # 森林中树的数量 (旧版参数名可能是 n_estimators) min_leaf_size=10, # 每片叶子节点最少的样本数 max_depth=20, # 每棵树的最大深度 subsample_ratio=subsample_ratio, # 构建每棵树时使用的样本比例 # 倾向得分模型: 使用带 L1 惩罚的逻辑回归 (solver='saga' 支持 L1) # C 是正则化强度的倒数，这里根据 lambda_reg 计算 propensity_model=LogisticRegression(C=1 / (X.shape[0] * lambda_reg), penalty='l1', solver='saga'), # 结果模型: 使用 Lasso 回归 (L1 惩罚) model_Y=Lasso(alpha=lambda_reg), # DML 最后阶段的倾向得分模型 (可以与初始模型相同或不同) propensity_model_final=LogisticRegression(C=1 / (X.shape[0] * lambda_reg), penalty='l1', solver='saga'), # DML 最后阶段的结果模型 (使用带权重的 Lasso) model_Y_final=WeightedLasso(alpha=lambda_reg), n_jobs=1 # 使用的 CPU 核心数 (1 表示不并行，避免某些环境下的问题))

   训练 DROrthoForest 模型print("Starting DROrthoForest training...")# Y: 结果变量, T: 处理变量, X: 异质性来源, W: 控制变量est.fit(Y, T, X=X, W=W)print("DROrthoForest training finished.")

   计算在测试点 X_test 上的处理效应 (CATE)treatment_effects = est.effect(X_test)# 计算处理效应的 95% 置信区间 (使用 BLB 方法)te_lower, te_upper = est.effect_interval(X_test, alpha=0.05) # alpha=0.05 表示 95% 置信度print("DROrthoForest effect estimation finished.")

   --- CausalForestDML ---

   创建 CausalForestDML 估计器实例est2 = CausalForestDML( model_y=Lasso(alpha=lambda_reg), # 结果模型 (Y ~ W + X) model_t=LogisticRegression(C=1 / (X.shape[0] * lambda_reg), penalty='l1', solver='saga'), # 处理模型 (T ~ W + X), 使用 penalty='l1' 和 saga solver n_estimators=200, # 森林中树的数量 min_samples_leaf=5, # 叶子节点最小样本数 max_depth=50, # 树的最大深度 max_samples=subsample_ratio / 2, # 构建每棵树时抽取的样本比例 (这里设得比 DROrthoForest 小) discrete_treatment=True, # 指明 T 是离散变量 (0/1) random_state=123, # 随机种子，保证结果可复现 n_jobs=1 # 使用 CPU 核心数)

   训练 CausalForestDML 模型print("Starting CausalForestDML training...")# cache_values=True 可以缓存中间计算结果，加速后续 effect 等方法的调用est2.fit(Y, T, X=X, W=W, cache_values=True)print("CausalForestDML training finished.")

   计算在测试点 X_test 上的处理效应 (CATE)treatment_effects2 = est2.effect(X_test)# 计算 CATE 的 95% 置信区间te_lower2, te_upper2 = est2.effect_interval(X_test, alpha=0.05)print("CausalForestDML effect estimation finished.")

   打印第二个模型 (CausalForestDML) 的摘要信息# 可能包含估计的平均处理效应 (ATE) 及其标准误等print("\nCausalForestDML Summary:")try: print(est2.summary())except AttributeError: print("Summary method not available for this version or configuration.")

   --- 可视化比较两个森林模型的结果 ---plt.figure(figsize=(15, 6)) # 创建一个宽一点的图形容纳两个子图

   计算真实的 TE(x) 用于比较expected_te = np.array([exp_te(x_i) for x_i in X_test])

   左侧子图：DROrthoForest 结果plt.subplot(1, 2, 1) # 1行2列的第1个plt.title("DROrthoForest CATE Estimation")# 绘制 DROrthoForest 估计的 CATE 曲线plt.plot(X_test[:, 0], treatment_effects, label='DROrthoForest CATE Estimate', color='tab:orange')# 绘制真实的 TE 曲线plt.plot(X_test[:, 0], expected_te, 'b--', label='True Effect (Ground Truth)')# 填充置信区间区域plt.fill_between(X_test[:, 0], te_lower, te_upper, color='tab:orange', alpha=0.3, label="95% Confidence Interval (BLB)")plt.ylabel("Treatment Effect (CATE)")plt.xlabel("Heterogeneity Feature (X)")plt.legend(loc='upper left', prop={'size': 10}) # 调整图例位置和大小plt.grid(True, linestyle='--', alpha=0.6)

   右侧子图：CausalForestDML 结果plt.subplot(1, 2, 2) # 1行2列的第2个plt.title("CausalForestDML CATE Estimation")# 绘制 CausalForestDML 估计的 CATE 曲线plt.plot(X_test[:, 0], treatment_effects2, label='CausalForestDML CATE Estimate', color='tab:green')# 绘制真实的 TE 曲线plt.plot(X_test[:, 0], expected_te, 'b--', label='True Effect (Ground Truth)')# 填充置信区间区域plt.fill_between(X_test[:, 0], te_lower2, te_upper2, color='tab:green', alpha=0.3, label="95% Confidence Interval")plt.ylabel("Treatment Effect (CATE)")plt.xlabel("Heterogeneity Feature (X)")plt.legend(loc='upper left', prop={'size': 10})plt.grid(True, linestyle='--', alpha=0.6)

   plt.tight_layout() # 调整子图布局防止重叠plt.show()

   计算真实的平均处理效应 (Average Treatment Effect, ATE) 作为参考# 在我们的模拟中，可以通过对真实 TE(x) 在 X 的分布上积分得到# 这里用测试点上的 TE 均值近似 ATEATE_for_cf = np.mean(expected_te)print(f"\nApproximate True Average Treatment Effect (ATE): {ATE_for_cf:.4f}")

   --- 创建并使用另一个 CausalForestDML 实例进行不同的推断 ---

   创建一个新的 CausalForestDML 实例，使用不同的参数配置est_inf = CausalForestDML( cv=2, # 交叉拟合的折数 criterion='mse', # 森林分裂的标准 (均方误差) n_estimators=400, # 更多的树 min_var_fraction_leaf=0.1, # 叶子节点样本占总样本最小比例 (控制复杂度) min_var_leaf_on_val=True, # 在验证集上检查叶节点方差条件 verbose=0, # 不打印训练过程信息 discrete_treatment=False, # !! 注意：这里设为 False。对于二元T，两种设置有时都可用，但内部处理可能不同。 # 设为 False 可能启用处理连续 T 的逻辑，但对二元 T 仍能估计效应。 n_jobs=1, # CPU核心数 random_state=123 # 随机种子)print("\nStarting second CausalForestDML (for inference) training...")est_inf.fit(Y, T, X=X, W=W)print("Second CausalForestDML training finished.")

   --- 边际效应推断 (Marginal Effect Inference) ---# 估计平均边际效应，即假设效应对于所有X是恒定的print("Performing constant marginal effect inference...")res_me = est_inf.const_marginal_effect_inference(X_test)point_me = res_me.point_estimate # 平均效应的点估计lb_me, ub_me = res_me.conf_int(alpha=.01) # 99% 置信区间

   可视化平均边际效应 (常数线)plt.figure(figsize=(10, 6))

   plt.plot(X_test[:, 0], point_me * np.ones_like(X_test[:, 0]), label=f'Const. Marginal Effect Estimate ({point_me[0]:.2f})', color='tab:red')plt.fill_between(X_test[:, 0], lb_me * np.ones_like(X_test[:, 0]), ub_me * np.ones_like(X_test[:, 0]), color='tab:red', alpha=0.3, label='99% CI for Const. Marginal Effect')# 同时绘制真实的异质性效应作为对比plt.plot(X_test[:, 0], expected_te, 'b--', label='True Heterogeneous Effect')plt.xlabel("Heterogeneity Feature (X)")plt.ylabel("Treatment Effect")plt.title("Constant Marginal Effect Inference vs True Effect")plt.legend(loc='upper left', prop={'size': 10})plt.grid(True, linestyle='--', alpha=0.6)plt.show()

   打印边际效应推断的摘要信息print("\nConstant Marginal Effect Inference Summary:")print(res_me.summary_frame())

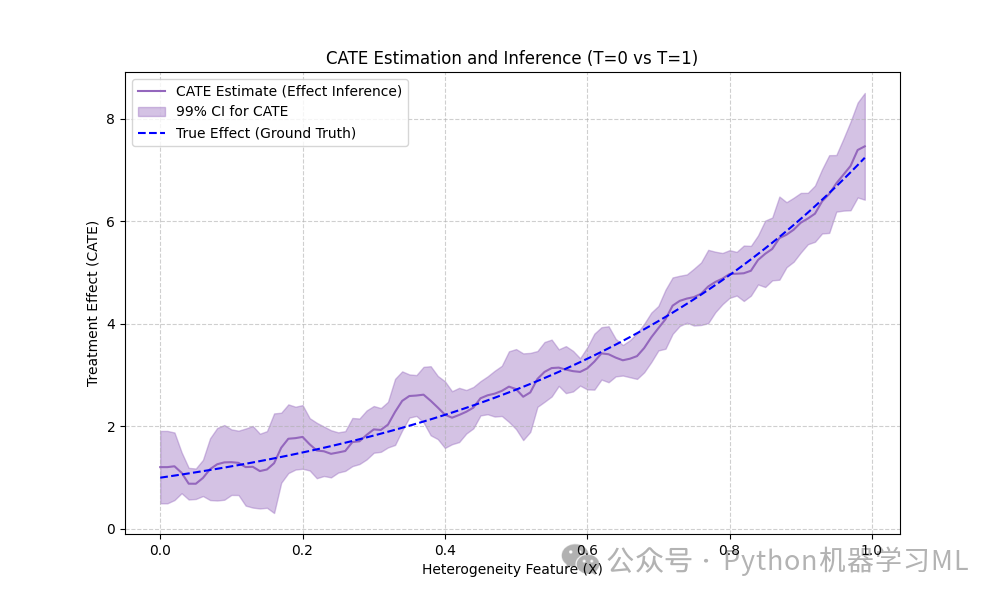
   --- 处理效应推断 (Effect Inference for T=0 vs T=1) ---# 专门估计从 T=0 变化到 T=1 的处理效应 (即 CATE)print("\nPerforming effect inference (CATE)...")# T0 和 T1 定义了我们想比较的两个处理水平res_cate = est_inf.effect_inference(X_test, T0=0, T1=1) # 对于二元T，T0=0, T1=1 是标准做法point_cate = res_cate.point_estimate # CATE(x) 的点估计lb_cate, ub_cate = res_cate.conf_int(alpha=0.01) # CATE(x) 的 99% 置信区间

   可视化 CATE 推断结果plt.figure(figsize=(10, 6))plt.plot(X_test[:, 0], point_cate, label='CATE Estimate (Effect Inference)', color='tab:purple')plt.fill_between(X_test[:, 0], lb_cate, ub_cate, alpha=.4, color='tab:purple', label='99% CI for CATE')plt.plot(X_test[:, 0], expected_te, 'b--', label='True Effect (Ground Truth)')plt.xlabel("Heterogeneity Feature (X)")plt.ylabel("Treatment Effect (CATE)")plt.title("CATE Estimation and Inference (T=0 vs T=1)")plt.legend(loc='upper left', prop={'size': 10})plt.grid(True, linestyle='--', alpha=0.6)plt.show()

---

第五阶段：聚类分析

目的: 基于估计出的异质性处理效应 (CATE) 和/或其他特征，将样本分成不同的组（簇），探索是否存在具有相似处理效应模式的子群体。

讲解: 这一阶段使用经典的 K-Means 聚类算法 来发现数据中的群体结构。

1. 寻找最佳聚类数量 (K):

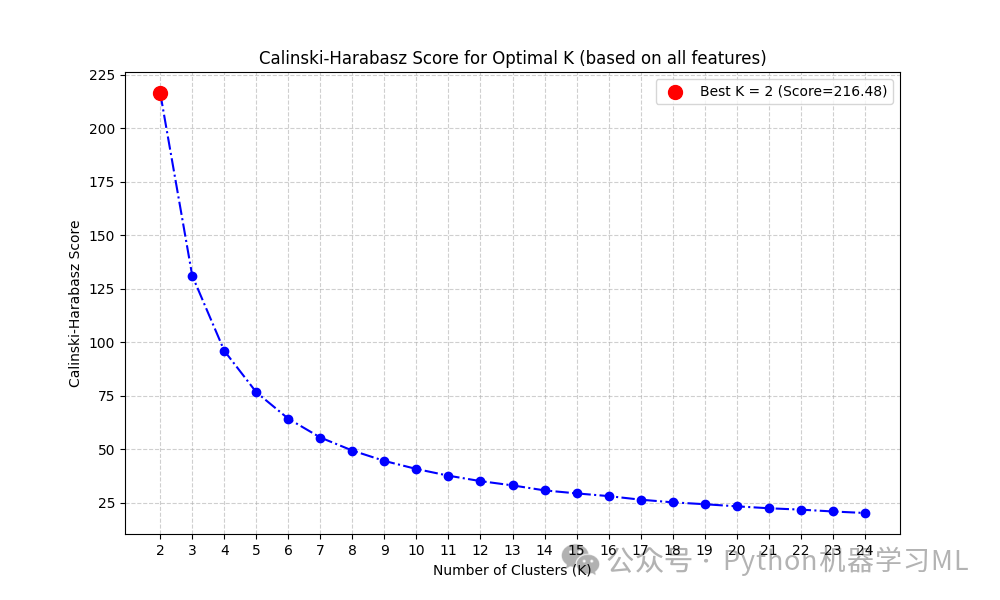
   • CH 指数衡量簇间离散度与簇内离散度的比率。分数越高通常表示聚类效果越好（簇本身紧密，簇之间分离度高）。

   • 对于每个 K，运行 K-Means 并计算 CH 分数。

   • 绘制 CH Score vs K 的曲线，选择使得分最高的 K 值。

   • 注意:

     代码中计算 CH 分数时 kmeans = KMeans(n_clusters=i, random_state=1).fit(total_frame) 使用了整个 total_frame（包含 CATE 置信区间、点估计、X 和 W）作为聚类特征。这与计算 WCSS 时使用的特征不同，需要注意。通常建议在同一组特征上应用这两种方法来选择 K。

   • 尝试不同的 K 值（这里是从 2 到 24）。

   • 对于每个 K，运行 K-Means 并计算 WCSS (Within-Cluster Sum of Squares)，即每个簇内样本点到其质心距离的平方和。

   • 绘制 WCSS vs K 的曲线。理想情况下，曲线会像一个手臂，WCSS 随着 K 增大而减小，在某个 K 值（"肘部"）之后下降速率显著减缓。这个"肘部"通常被认为是较好的 K 值。

   • 注意:

     代码中计算 WCSS 时 kmeans_pca.fit(point.reshape(-1, 1)) 只使用了 CATE 点估计 point_orig (来自训练数据的CATE) 作为聚类特征。

   • K-Means 需要预先指定簇的数量 K。通常我们不知道最佳的 K 是多少。

   • 肘部法则 (Elbow Method):

   • Calinski-Harabasz (CH) 指数:

2. 执行聚类:

   • 根据肘部法则或 CH 指数选择一个"最优"的 K。代码隐式地选择了使 CH 分数最高的 K，并存储了对应的聚类标签 hc_labels[np.argmax(hc_metrics)]。

3. 可视化聚类结果:

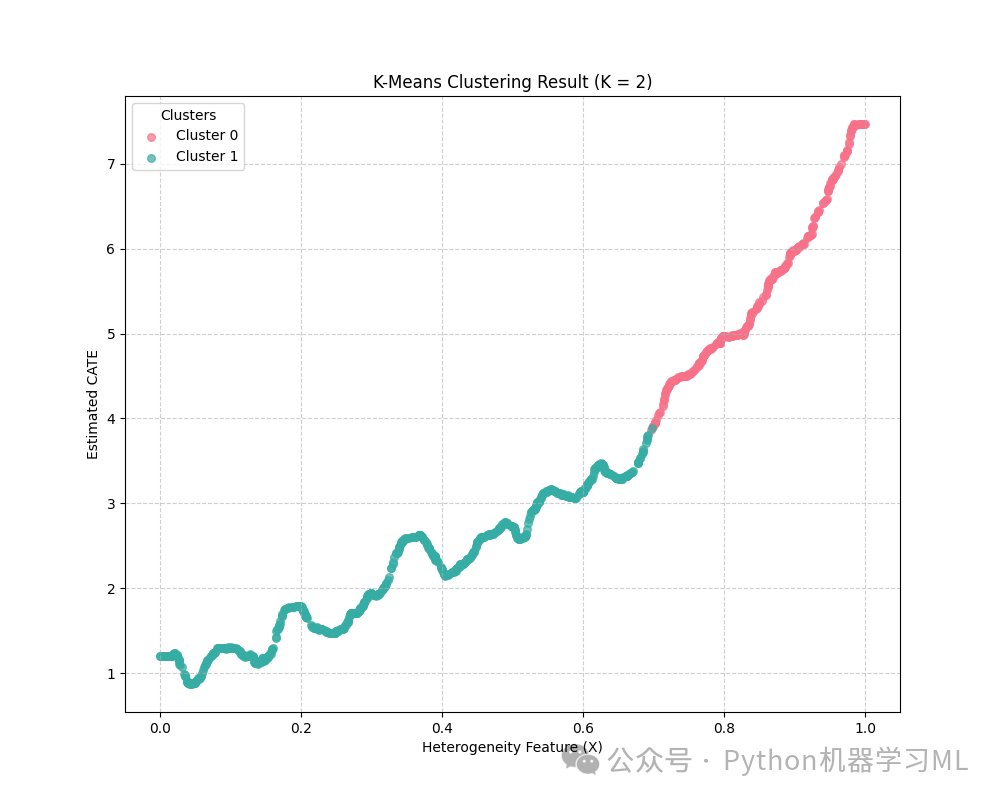
   • 代码绘制了一个散点图。

   • X 轴是异质性特征 X（total_frame[:, 3]，因为前三列是效应估计）。

   • Y 轴是 CATE 的点估计（total_frame[:, 2]）。

   • 图中不同的颜色代表 K-Means 找到的不同簇。

   • 通过观察图，我们可以看到具有不同 X 值和不同估计效应 CATE 的样本是如何被分到不同组的，从而理解处理效应的异质性模式。

聚类的意义: 发现这些子群体有助于：

• 理解哪些人群对处理更敏感（效应高）或不敏感（效应低）。

• 为不同群体制定差异化的干预策略（个性化决策）。

• 进一步探索为什么这些群体的效应不同（可能与 X 或 W 中的某些特定变量有关）。

# 导入聚类和降维相关库from sklearn.cluster import KMeans # K-Means 聚类算法from sklearn.decomposition import PCA # 主成分分析 (这里没用到，但常与聚类结合)from sklearn import metrics # 包含多种聚类效果评估指标from sklearn.metrics import pairwise_distances # 用于计算距离 (这里没直接用到)import numpy as np
# --- 评估不同聚类数量 K 的效果 ---
wcss = []  # 存储 WCSS (Within-Cluster Sum of Squares) 用于肘部法则hc_metrics = []  # 存储 Calinski-Harabasz 分数hc_labels = []  # 存储每个 K 值对应的聚类标签
# 尝试 K 从 2 到 24print("\nEvaluating different numbers of clusters (K)...")k_range = range(2, 25)for i in k_range:    # 1. 使用 CATE 点估计进行 K-Means，计算 WCSS (用于肘部法则)    # 注意：这里只用了 CATE 点估计 point_orig (来自训练集) 作为特征    kmeans_pca = KMeans(n_clusters=i, init='k-means++', random_state=42, n_init=10) # n_init=10 多次初始化选最优    kmeans_pca.fit(point_orig.reshape(-1, 1)) # 需要 reshape 成 N x 1 的二维数组    wcss.append(kmeans_pca.inertia_)  # inertia_ 属性就是 WCSS
    # 2. 使用整个 total_frame 进行 K-Means，计算 CH 分数和存储标签    # 注意：这里使用了所有特征 (CATE CI, CATE point, X, W)    kmeans = KMeans(n_clusters=i, random_state=1, n_init=10) # 随机种子不同于上面    kmeans.fit(total_frame)    labels = kmeans.labels_  # 获取每个样本所属的簇标签    hc_labels.append(labels)  # 存储这组标签    # 计算 CH 分数，需要原始数据和标签    # 如果样本量很大，这个计算可能较慢    try:        score = metrics.calinski_harabasz_score(total_frame, labels)        hc_metrics.append(score)    except ValueError:        # 如果只有一个簇或者数据有问题，可能会报错        hc_metrics.append(np.nan) # 添加 NaN 值        print(f"Warning: Could not compute CH score for K={i}")    score = hc_metrics[-1]    ch_score_str = f'{score:.2f}' if not np.isnan(score) else 'NaN'
    print(f" K={i}: WCSS={wcss[-1]:.2f}, CH Score={ch_score_str}")
# --- 绘制评估曲线 ---
# 绘制肘部法则图 (WCSS vs K)plt.figure(figsize=(10, 6))plt.plot(k_range, wcss, marker='o', linestyle='-.', color='red')plt.xlabel('Number of Clusters (K)')plt.ylabel('WCSS (Within-Cluster Sum of Squares)')plt.title('Elbow Method for Optimal K (based on CATE point only)')plt.xticks(k_range) # 显示所有K值刻度plt.grid(True, linestyle='--', alpha=0.6)plt.show()
# 绘制 Calinski-Harabasz 分数图 (CH Score vs K)# 过滤掉 NaN 值以防绘图错误valid_k = [k for k, score in zip(k_range, hc_metrics) if not np.isnan(score)]valid_scores = [score for score in hc_metrics if not np.isnan(score)]
if valid_scores: # 确保有合法的分数可供绘制    plt.figure(figsize=(10, 6))    plt.plot(valid_k, valid_scores, marker='o', linestyle='-.', color='blue') # 使用不同的颜色    plt.xlabel('Number of Clusters (K)')    plt.ylabel('Calinski-Harabasz Score')    plt.title('Calinski-Harabasz Score for Optimal K (based on all features)')    # 标记最高分对应的 K    best_k_ch = valid_k[np.argmax(valid_scores)]    max_score = np.max(valid_scores)    plt.scatter(best_k_ch, max_score, color='red', s=100, zorder=5, label=f'Best K = {best_k_ch} (Score={max_score:.2f})')    plt.xticks(valid_k)    plt.legend()    plt.grid(True, linestyle='--', alpha=0.6)    plt.show()else:    print("No valid Calinski-Harabasz scores were computed.")    best_k_ch = -1 # 标记为无效
# --- 可视化最优聚类结果 (基于 CH 分数最高的 K) ---
if best_k_ch != -1:    print(f"\nVisualizing clusters for the best K = {best_k_ch} (based on CH score)...")    # 获取最佳 K 对应的标签    best_labels = hc_labels[valid_k.index(best_k_ch)] # 注意索引对应关系
    plt.figure(figsize=(10, 8))    # 使用 seaborn 的调色板获取不同颜色    palette = sns.color_palette("husl", best_k_ch)    # 遍历每个簇 (0 到 best_k_ch-1)    for i in np.unique(best_labels):        # 找到属于当前簇 i 的所有样本的索引        spots = np.where(best_labels == i)        # 绘制这些样本点        # X轴: total_frame[:, 3] (即第一个协变量 X[:, 0])        # Y轴: total_frame[:, 2] (即 CATE 的点估计 point_orig)        plt.scatter(total_frame[spots, 3], total_frame[spots, 2],                    label=f'Cluster {i}', color=palette[i], alpha=0.7, s=30) # s控制点大小
    plt.xlabel('Heterogeneity Feature (X)')    plt.ylabel('Estimated CATE')    plt.title(f'K-Means Clustering Result (K = {best_k_ch})')    plt.legend(title='Clusters')    plt.grid(True, linestyle='--', alpha=0.6)    plt.show()else:    print("Cannot visualize clusters as no best K was determined.")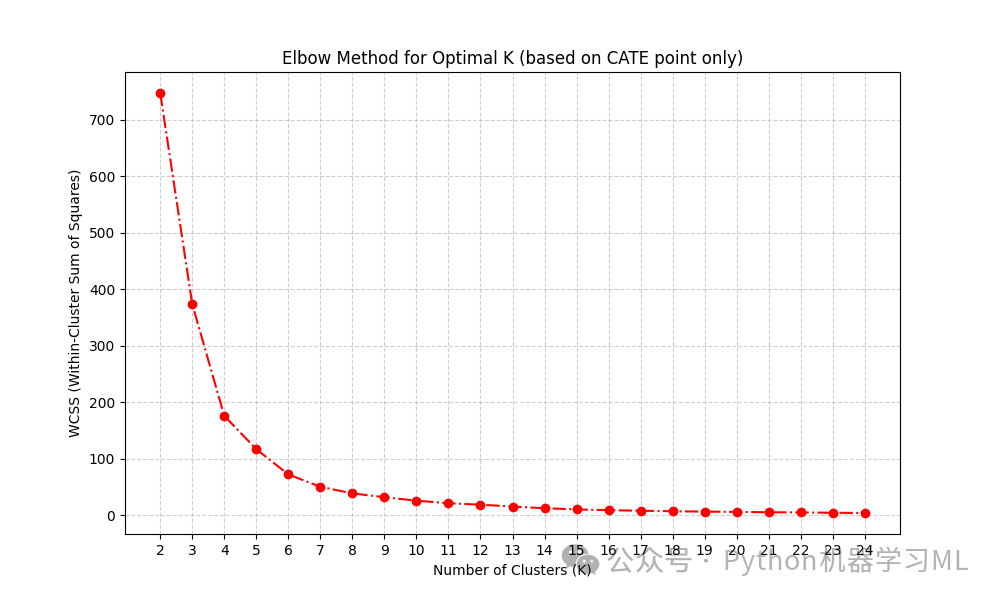

应用到其他数据集的关键步骤

要将本教程介绍的因果推断流程和模型应用到您自己的数据集，您需要遵循以下关键步骤：

1. 明确因果问题与数据准备:

   • 结果变量 Y (Outcome):

     你最终关心的那个结果指标是什么？（例如：销售额、用户留存率、康复时间）

   • 处理变量 T (Treatment):

     你想评估其效果的干预、行动或特征是什么？它是二元的（如用药/未用药）还是连续的（如广告投入金额）？

   • 协变量 X (Covariates / Features for Heterogeneity):

     你认为哪些个体特征可能会调节处理变量的效果？（例如：用户年龄、用户地理位置、产品类别）

   • 控制变量 W (Controls / Confounders):

     哪些变量同时影响 了个体接受处理的可能性 T 和 结果 Y？必须尽可能全面地识别并包含这些变量，以控制混淆。（例如：用户的历史购买行为、病情严重程度、学生入学前的基础）

   • 工具变量 Z (Instrumental Variable):

     （仅当使用 IV 方法如 DeepIV 时需要）是否存在一个变量 Z，它能影响个体接受处理 T 的决策，但它本身不会直接影响结果 Y（除非通过 T 产生影响），并且 Z 与 Y 的未观测影响因素无关？寻找有效的 Z 非常困难，需要很强的领域知识和严格的检验。

   • 定义变量:

     清晰地界定你的目标：

   • 数据收集与清洗:

     收集包含上述所有变量的数据。进行必要的数据清洗、处理缺失值、转换数据类型等。

   • 数据合并:

     确保所有变量都在一个统一的数据结构中（如 Pandas DataFrame）。

2. 选择合适的因果模型:

   • 是否存在内生性/未观测混淆？

     如果你强烈怀疑有重要的未观测混淆因素，并且能找到有效的工具变量 Z ，那么 DeepIV 是一个可以考虑的强大选项。

   • 是否主要关心异质性处理效应 (HTE)？

     如果你想了解处理效果如何随个体特征 X 变化，并且假设你已经包含了足够多的控制变量 W 来处理主要的混淆，那么基于 DML 的森林方法如 DROrthoForest 或 CausalForestDML 是非常好的选择。它们对 W 的建模有较好的鲁棒性。

   • 处理变量 T 是离散还是连续的？

     确保所选模型的参数设置与你的 T 类型匹配（例如 CausalForestDML 中的 discrete_treatment 参数）。

   • 数据量大小:

     深度学习模型（如 DeepIV）通常需要较大数据量。森林模型在中小规模数据上表现也很好。

3. 模型配置与训练:

   • 正则化:

     对于 Lasso/Ridge 等线性模型，正则化强度（如 alpha 或 C）很重要，可能需要通过交叉验证选择，或者使用类似代码中基于理论的启发式计算。

   • 森林参数:

     树的数量 (n_estimators/n_trees)、树深 (max_depth)、叶节点大小 (min_samples_leaf/min_leaf_size)、子采样比例 (max_samples/subsample_ratio) 等都需要根据数据情况调整，以平衡偏差和方差。

   • 神经网络参数:

     对于 DeepIV，网络结构（层数、节点数）、激活函数、优化器、学习率、正则化、Dropout 比例等都需要仔细设计和调整。

   • 选择内部估计器:

     对于 DML 方法，你需要为结果模型 (model_y) 和处理/倾向得分模型 (model_t) 选择合适的机器学习模型（如 Lasso, Ridge, GradientBoostingRegressor/Classifier, 甚至其他森林）。模型的选择会影响最终效果。

   • 调整超参数:

   • 执行训练:

     使用 fit(Y, T, X=X, W=W, Z=Z) （根据模型需要传入相应变量）来训练模型。

4. 估计与解释因果效应:

   • 估计 CATE:

     使用 effect(X_new) 方法估计在新数据点 X_new （或者原始数据 X）上的条件平均处理效应。

   • 估计 ATE:

     有些模型提供直接估计平均处理效应（ATE）的方法（如 est.ate() 或在 summary() 中查看），或者可以通过对 CATE(X) 在 X 的分布上求平均来近似得到 ATE。

   • 计算置信区间:

     使用 effect_interval() 或 effect_inference() 等方法获取效应估计的置信区间，这对于理解估计的不确定性至关重要。一个很宽的置信区间意味着估计结果不太可靠。

   • 可视化:

     绘制 CATE(x) 随某个重要特征 x 变化的曲线图（类似教程中的做法），并带上置信区间。这有助于直观理解异质性。

   • 解读结果:

     结合业务或领域知识来解释估计出的因果效应的大小、方向和异质性模式是否有意义。效应是正向还是负向？统计上是否显著（置信区间是否包含0）？哪些人群受益最多/最少？

5. 敏感性分析与模型检验 (重要但本项目未深入):

   • 检验假设:

     对于 IV 方法，需要检验工具变量的有效性。对于 DML 方法，虽然对模型设定有鲁棒性，但仍需检查内部模型拟合情况。

   • 安慰剂检验 (Placebo Tests):

     例如，将一个已知没有效应的变量作为"处理"变量，看模型是否（错误地）估计出显著效应。

   • 对未观测混淆的敏感性分析:

     尝试量化结果对可能存在的、未包含在 W 中的混淆因素的敏感程度。EconML 也提供了一些相关工具。

6. 发现子群体 (可选):

   • 如果对发现具有相似效应模式的子群体感兴趣，可以像教程中那样，使用估计出的 CATE 或其他相关特征进行聚类分析（如 K-Means）。

   • 分析每个簇的特征（X 和 W 的分布），理解造成效应差异的原因。

通过遵循这些步骤，并结合对 EconML 库文档的进一步学习，应该能够将这些强大的因果推断技术应用于您自己的实际问题中。记住，因果推断往往比单纯的预测更具挑战性，需要更仔细的思考、假设检验和结果解读。