d-堆，左式堆及斜堆的简单介绍

d-堆介绍

二叉堆就是d-堆中d为2的简单推广，d-堆的每个节点都有d个子节点，同时保持堆的性质。

d-堆也用数组存储数据，其父节点下标和子节点下标的关系也很可以用数学公式获得，插入元素时，也是先在数组元素的最后一个位置插入，然后通过上浮操作保持堆结构的性质，删除根节点极值元素后再通过下浮操作保持堆结构的性质。具体代码如下：

d-堆实现

程序由豆包生成

cpp 复制代码

//
// Created by Administrator on 2025/12/10.
//
#include <stdio.h>
#include <stdlib.h>
#include <stdbool.h>

// 定义d堆结构体
typedef struct {
    int* data;       // 存储堆元素的数组
    int capacity;    // 堆的容量
    int size;         // 堆当前元素个数
    int d;            // 每个节点的子节点数（d-ary）
} DHeap;

// 创建d堆（初始化）
DHeap* createDHeap(int capacity, int d) {
    if (d < 2) { // 子节点数至少为2，否则退化为链表
        printf("d必须大于等于2！\n");
        return NULL;
    }
    DHeap* heap = (DHeap*)malloc(sizeof(DHeap));
    heap->data = (int*)malloc(sizeof(int) * capacity);
    heap->capacity = capacity;
    heap->size = 0;
    heap->d = d;
    return heap;
}

// 获取索引为i的节点的第k个子节点的索引（k从1到d）
int getChildIndex(DHeap* heap, int i, int k) {
    if (k < 1 || k > heap->d) {
        return -1; // 无效的子节点编号
    }
    return heap->d * i + k;
}

// 获取索引为i的节点的父节点索引
int getParentIndex(DHeap* heap, int i) {
    if (i == 0) { // 根节点无父节点
        return -1;
    }
    return (i - 1) / heap->d;
}

// 交换两个元素
void swap(int* a, int* b) {
    int temp = *a;
    *a = *b;
    *b = temp;
}

// 上浮操作（插入元素后调整，维持大顶堆性质）
void heapifyUp(DHeap* heap, int index) {
    int parent = getParentIndex(heap, index);
    // 如果当前节点大于父节点，交换并继续上浮
    while (index > 0 && heap->data[index] > heap->data[parent]) {
        swap(&heap->data[index], &heap->data[parent]);
        index = parent;
        parent = getParentIndex(heap, index);
    }
}

// 下沉操作（删除堆顶后调整，维持大顶堆性质）
void heapifyDown(DHeap* heap, int index) {
    int maxChildIndex;
    int child;
    while (true) {
        maxChildIndex = index; // 初始假设当前节点是最大的
        // 遍历所有子节点，找到值最大的子节点
        for (child = 1; child <= heap->d; child++) {
            int childIdx = getChildIndex(heap, index, child);
            if (childIdx < heap->size && heap->data[childIdx] > heap->data[maxChildIndex]) {
                maxChildIndex = childIdx;
            }
        }
        // 如果最大子节点大于当前节点，交换并继续下沉；否则结束
        if (maxChildIndex != index) {
            swap(&heap->data[index], &heap->data[maxChildIndex]);
            index = maxChildIndex;
        } else {
            break;
        }
    }
}

// 插入元素到d堆
bool insert(DHeap* heap, int value) {
    if (heap == NULL) {
        return false;
    }
    if (heap->size == heap->capacity) { // 堆已满
        printf("堆已满，无法插入！\n");
        return false;
    }
    // 插入到数组末尾，然后上浮调整
    heap->data[heap->size] = value;
    heapifyUp(heap, heap->size);
    heap->size++;
    return true;
}

// 删除并返回堆顶元素（大顶堆的最大值）
int extractMax(DHeap* heap) {
    if (heap == NULL || heap->size == 0) { // 堆为空
        printf("堆为空，无法删除！\n");
        return -1; // 用-1表示失败（假设堆中无负数，实际可根据场景调整）
    }
    int max = heap->data[0]; // 堆顶是最大值
    // 将最后一个元素移到堆顶，然后下沉调整
    heap->data[0] = heap->data[heap->size - 1];
    heap->size--;
    heapifyDown(heap, 0);
    return max;
}

// 打印d堆（层序遍历）
void printDHeap(DHeap* heap) {
    if (heap == NULL || heap->size == 0) {
        printf("堆为空！\n");
        return;
    }
    printf("d堆元素（层序）：");
    for (int i = 0; i < heap->size; i++) {
        printf("%d ", heap->data[i]);
    }
    printf("\n");
}

// 释放d堆内存
void freeDHeap(DHeap* heap) {
    if (heap != NULL) {
        free(heap->data);
        free(heap);
    }
}

// 测试示例
int main() {
    // 创建一个容量为10、每个节点有3个子节点的d堆（3叉堆）
    DHeap* heap = createDHeap(10, 3);

    // 插入元素
    insert(heap, 5);
    insert(heap, 3);
    insert(heap, 8);
    insert(heap, 1);
    insert(heap, 10);
    printDHeap(heap); // 输出：10 3 8 1 5（大顶堆，根节点最大）

    // 删除堆顶（最大值10）
    printf("删除的堆顶元素：%d\n", extractMax(heap));
    printDHeap(heap); // 输出：8 3 5 1（新的大顶堆）

    freeDHeap(heap);
    return 0;
}

结果如下：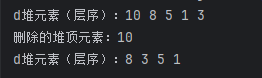

左式堆介绍

把两个二叉堆合并是一个比较复杂的操作，左式堆就可以很高效地完成合并操作。

左式堆通过路径长度(NPL)的约束使树的形态向左倾斜,NPL就是某个节点到最近的没有两个子节点的节点经过的节点数量。若节点是空节点，那它的NPL就是-1，一般节点的的NPL为其两个子节点的NPL最小值+1.同时所以节点的左子节点NPL必须大于等于其右子节点的NPL。

其核心操作就是合并(merge)，首先合并的堆其根节点肯定是取两个要合并堆H1,H2的根节点的那个极值(假设H1的根节点是极值)，其H1的根就是合并后堆的根。然后通过递归的方式合并H1的右子树和H2，由于H1的左子树已经都小于合并后堆的根，所以不用进行合并操作了。同时每递归合并一个元素(就是把H2的每个插入到H1的右子树上后)，再对H1(当前递归层的主堆根节点)左右子节点的NPL值进行维护。这样层层递归的结果就是得到一个合并后的左式堆。实现代码如下：

左式堆实现

程序由豆包生成

cpp 复制代码

//
// Created by Administrator on 2025/12/10.
//
#include <stdio.h>
#include <stdlib.h>

// 左式堆节点结构体
typedef struct LeftistNode {
    int key;                // 节点值
    int npl;                // 空路径长度（NPL）
    struct LeftistNode *left;  // 左子节点
    struct LeftistNode *right; // 右子节点
} LeftistNode, *LeftistHeap;

// 创建空节点
LeftistNode* createNode(int key) {
    LeftistNode* node = (LeftistNode*)malloc(sizeof(LeftistNode));
    node->key = key;
    node->npl = 0; // 叶子节点NPL初始为0
    node->left = NULL;
    node->right = NULL;
    return node;
}

// 获取节点的NPL（处理空节点）
int getNPL(LeftistNode* node) {
    return node == NULL ? -1 : node->npl;
}

// 交换节点的左右子树（维护左式堆性质）
void swapChildren(LeftistNode* node) {
    LeftistNode* temp = node->left;
    node->left = node->right;
    node->right = temp;
}

// 合并两个左式堆（核心操作）
LeftistNode* merge(LeftistNode* heap1, LeftistNode* heap2) {
    // 基准情况：其中一个堆为空，返回另一个
    if (heap1 == NULL) return heap2;
    if (heap2 == NULL) return heap1;

    // 保证heap1的根节点值更小（小顶堆），否则交换两个堆
    if (heap1->key > heap2->key) {
        LeftistNode* temp = heap1;
        heap1 = heap2;
        heap2 = temp;
    }

    // 递归合并heap1的右子堆和heap2
    heap1->right = merge(heap1->right, heap2);

    // 维护左式堆性质：左子节点NPL ≥ 右子节点NPL
    if (getNPL(heap1->left) < getNPL(heap1->right)) {
        swapChildren(heap1);
    }

    // 更新当前节点的NPL：1 + 最小子节点的NPL
    heap1->npl = getNPL(heap1->right) + 1;

    return heap1;
}

// 插入元素（等价于合并单节点堆和原堆）
LeftistHeap insert(LeftistHeap heap, int key) {
    LeftistNode* newNode = createNode(key);
    return merge(heap, newNode);
}

// 删除堆顶（最小值）：合并左右子堆
LeftistHeap deleteMin(LeftistHeap heap) {
    if (heap == NULL) {
        printf("堆为空，无法删除！\n");
        return NULL;
    }
    LeftistNode* left = heap->left;
    LeftistNode* right = heap->right;
    free(heap); // 释放原堆顶节点
    return merge(left, right);
}

// 前序遍历打印左式堆（用于验证）
void preOrder(LeftistNode* heap) {
    if (heap == NULL) return;
    printf("key: %d, NPL: %d\n", heap->key, heap->npl);
    preOrder(heap->left);
    preOrder(heap->right);
}

// 释放左式堆内存
void freeHeap(LeftistNode* heap) {
    if (heap == NULL) return;
    freeHeap(heap->left);
    freeHeap(heap->right);
    free(heap);
}

// 测试示例
int main() {
    // 构建第一个左式堆：插入5、3、8
    LeftistHeap heap1 = NULL;
    heap1 = insert(heap1, 5);
    heap1 = insert(heap1, 3);
    heap1 = insert(heap1, 8);
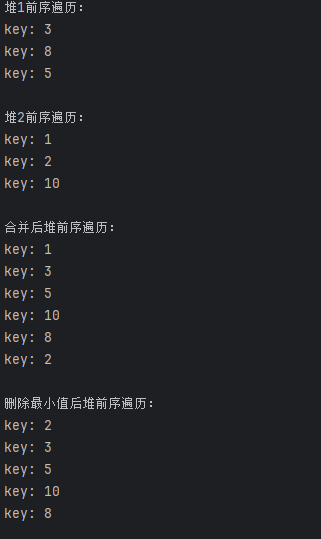
    printf("堆1前序遍历（key, NPL）：\n");
    preOrder(heap1); // 输出：3(1) → 5(0) → 8(0)（核心是根为3，左偏）

    // 构建第二个左式堆：插入1、10、2
    LeftistHeap heap2 = NULL;
    heap2 = insert(heap2, 1);
    heap2 = insert(heap2, 10);
    heap2 = insert(heap2, 2);
    printf("\n堆2前序遍历（key, NPL）：\n");
    preOrder(heap2); // 输出：1(1) → 2(0) → 10(0)

    // 合并两个堆
    LeftistHeap mergedHeap = merge(heap1, heap2);
    printf("\n合并后堆前序遍历（key, NPL）：\n");
    preOrder(mergedHeap); // 根为1，维持左式堆性质

    // 删除堆顶（最小值1）
    mergedHeap = deleteMin(mergedHeap);
    printf("\n删除最小值后堆前序遍历（key, NPL）：\n");
    preOrder(mergedHeap); // 新根为2

    freeHeap(mergedHeap);
    return 0;
}

结果如下：

斜堆介绍

斜堆就是左式堆的简易版，斜堆没有NPL的限制，所以其实现相对更简单。其合并操作也是通过递归将H1(H1的根是两个堆中的极值)的右子树和H2合并，合并完后还需要对H1进行左右子树交换，因为一般把H2的节点挂到H1的右子树后，H1的右子树会更大。交换完后H1大概率左斜，有利于之后的合并效率。具体实现如下：

斜堆实现

程序由豆包生成

cpp 复制代码

#include <stdio.h>
#include <stdlib.h>

// 斜堆节点结构体（无NPL字段，比左式堆更简洁）
typedef struct SkewNode {
    int key;                // 节点值
    struct SkewNode *left;  // 左子节点
    struct SkewNode *right; // 右子节点
} SkewNode, *SkewHeap;

// 创建单个节点
SkewNode* createNode(int key) {
    SkewNode* node = (SkewNode*)malloc(sizeof(SkewNode));
    node->key = key;
    node->left = NULL;
    node->right = NULL;
    return node;
}

// 交换节点的左右子树（核心辅助操作）
void swapChildren(SkewNode* node) {
    if (node == NULL) return;
    SkewNode* temp = node->left;
    node->left = node->right;
    node->right = temp;
}

// 合并两个斜堆（核心操作，无NPL）
SkewNode* merge(SkewNode* heap1, SkewNode* heap2) {
    // 基准条件：其中一个堆为空，返回另一个
    if (heap1 == NULL) return heap2;
    if (heap2 == NULL) return heap1;

    // 保证heap1的根节点更小（小顶堆），否则交换两个堆
    if (heap1->key > heap2->key) {
        SkewNode* temp = heap1;
        heap1 = heap2;
        heap2 = temp;
    }

    // 递归合并heap1的右子堆和heap2
    heap1->right = merge(heap1->right, heap2);

    // 斜堆核心：无条件交换左右子树（区别于左式堆的条件交换）
    swapChildren(heap1);

    return heap1;
}

// 插入元素（等价于合并单节点堆和原堆）
SkewHeap insert(SkewHeap heap, int key) {
    SkewNode* newNode = createNode(key);
    return merge(heap, newNode);
}

// 删除堆顶（最小值）：合并左右子堆
SkewHeap deleteMin(SkewHeap heap) {
    if (heap == NULL) {
        printf("堆为空，无法删除！\n");
        return NULL;
    }
    SkewNode* left = heap->left;
    SkewNode* right = heap->right;
    free(heap); // 释放原堆顶节点
    return merge(left, right);
}

// 前序遍历打印斜堆（验证结构）
void preOrder(SkewNode* heap) {
    if (heap == NULL) return;
    printf("key: %d\n", heap->key);
    preOrder(heap->left);
    preOrder(heap->right);
}

// 释放斜堆内存
void freeHeap(SkewNode* heap) {
    if (heap == NULL) return;
    freeHeap(heap->left);
    freeHeap(heap->right);
    free(heap);
}

// 测试示例
int main() {
    // 构建第一个斜堆：插入5、3、8
    SkewHeap heap1 = NULL;
    heap1 = insert(heap1, 5);
    heap1 = insert(heap1, 3);
    heap1 = insert(heap1, 8);
    printf("堆1前序遍历：\n");
    preOrder(heap1); // 输出随交换规则变化，但根一定是3（小顶堆）

    // 构建第二个斜堆：插入1、10、2
    SkewHeap heap2 = NULL;
    heap2 = insert(heap2, 1);
    heap2 = insert(heap2, 10);
    heap2 = insert(heap2, 2);
    printf("\n堆2前序遍历：\n");
    preOrder(heap2); // 根一定是1

    // 合并两个堆
    SkewHeap mergedHeap = merge(heap1, heap2);
    printf("\n合并后堆前序遍历：\n");
    preOrder(mergedHeap); // 根一定是1

    // 删除堆顶（最小值1）
    mergedHeap = deleteMin(mergedHeap);
    printf("\n删除最小值后堆前序遍历：\n");
    preOrder(mergedHeap); // 新根为2

    freeHeap(mergedHeap);
    return 0;
}

结果如下：