题目链接:
盛最多水的容器

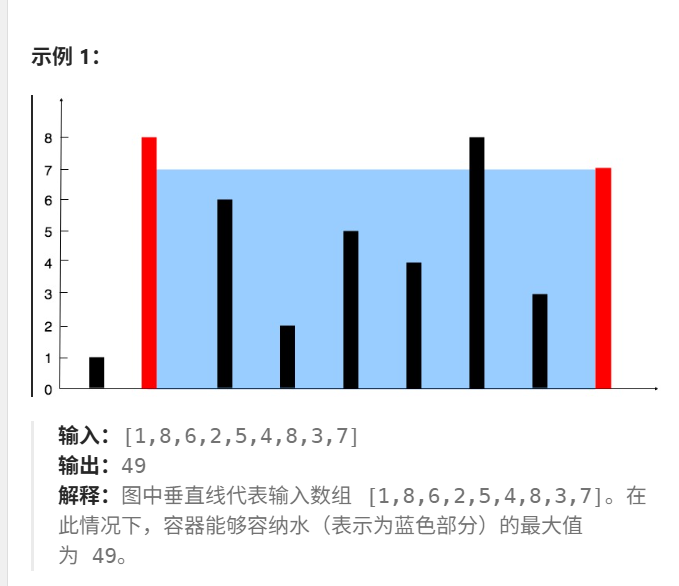
示例1:
 优选算法-004
优选算法-004
方法1:暴力破解
这个是最简单的方法,但是会超时
把所有的情况都算一遍,不断更新最大面积,循环结束,保留的结果就是最大面积
代码说明
- 核心逻辑 :通过双重循环枚举所有可能的左右指针组合(
i为左板,j为右板,且j > i); - 容积计算 :根据公式
容积 = 宽度 × 短板高度,其中宽度是j - i,高度是Math.min(height[i], height[j]); - 最大值更新:每次计算后,若当前容积大于已记录的最大值,则更新最大值。
复杂度分析
- 时间复杂度 :
O(n²)(双重循环遍历数组,n为数组长度),当n较大时会超时(例如 LeetCode 测试用例中n可达 10⁵,此时暴力解法会超出时间限制); - 空间复杂度 :
O(1)(仅使用常量级额外空间)。
java
public class Solution {
public int maxArea(int[] height) {
int maxVol = 0;
int n = height.length;
// 枚举所有可能的左指针i
for (int i = 0; i < n; i++) {
// 枚举所有可能的右指针j(j > i,避免重复计算)
for (int j = i + 1; j < n; j++) {
// 计算当前容器的宽度
int width = j - i;
// 计算当前容器的高度(取两板中的短板)
int h = Math.min(height[i], height[j]);
// 计算当前容积
int vol = width * h;
// 更新最大容积
if (vol > maxVol) {
maxVol = vol;
}
}
}
return maxVol;
}
}方法2:
双指针方法
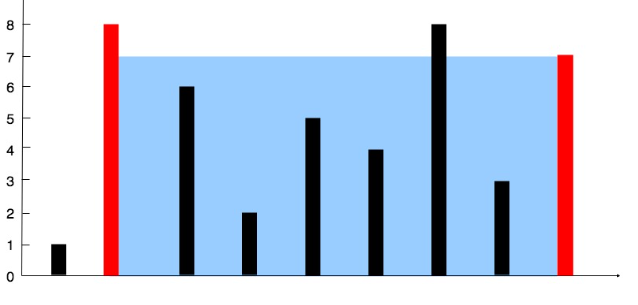
针对 "盛最多水的容器" 问题,双指针法是效率最高的解法,核心思路是通过左右指针向中间收缩,每次移动较短的那一侧指针,从而逼近最大容积
解法说明
- 指针初始化 :左指针
left从数组开头出发,右指针right从数组末尾出发; - 容积计算 :每次计算当前指针构成的容器容积(公式:
宽度 × 短板高度); - 指针移动逻辑 :
- 若左板更短:移动左指针(尝试找到更长的左板,提升高度);
- 若右板更短:移动右指针(尝试找到更长的右板,提升高度);
- 终止条件 :左右指针相遇时,遍历结束,此时
maxVol即为最大容积。
示例验证(输入[1,8,6,2,5,4,8,3,7])
- 初始指针:
left=0(高度 1)、right=8(高度 7),容积8×1=8; - 移动左指针→
left=1(高度 8),此时容积7×7=49(更新最大容积为 49); - 后续指针收缩过程中,容积均未超过 49,最终返回
49(与示例输出一致)。
复杂度分析
- 时间复杂度 :
O(n)(仅遍历数组一次); - 空间复杂度 :
O(1)(仅使用常量级额外空间)。
java
public class Solution {
public int maxArea(int[] height) {
int left = 0; // 左指针:初始指向数组左端
int right = height.length - 1; // 右指针:初始指向数组右端
int maxVol = 0; // 记录最大容积
while (left < right) {
// 计算当前容器的宽度
int width = right - left;
// 计算当前容器的高度(取左右指针中较短的板)
int h = Math.min(height[left], height[right]);
// 计算当前容积
int currentVol = width * h;
// 更新最大容积
maxVol = Math.max(maxVol, currentVol);
// 移动较短的那一侧指针(关键:缩短宽度的同时,尝试增加高度)
if (height[left] < height[right]) {
left++;
} else {
right--;
}
}
return maxVol;
}
}