排序算法锦集（一）

迷途之人不知返2025-12-12 8:49

排序

排序算法是一类非常重要的算法，因为我们在生活中，会见到各式各样的排序，比如排位、按时间排序、按使用时间排序，等等。

1、插入排序

1.1、直接插入排序

直接插入排序是指，在一个待排序的序列中，有一段已经排好的序列 。将已排好序列之后的元素，按顺序插入到已排好序列中，形成一个新的排好序列。

这就好比整理扑克牌，手上有一段已排好的牌，之后的牌，插到里面继续排好。

这里给出一个动图：

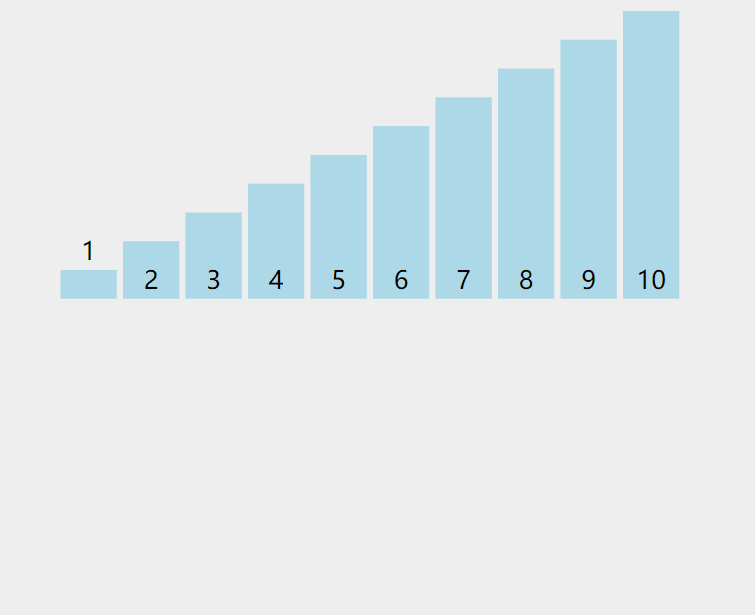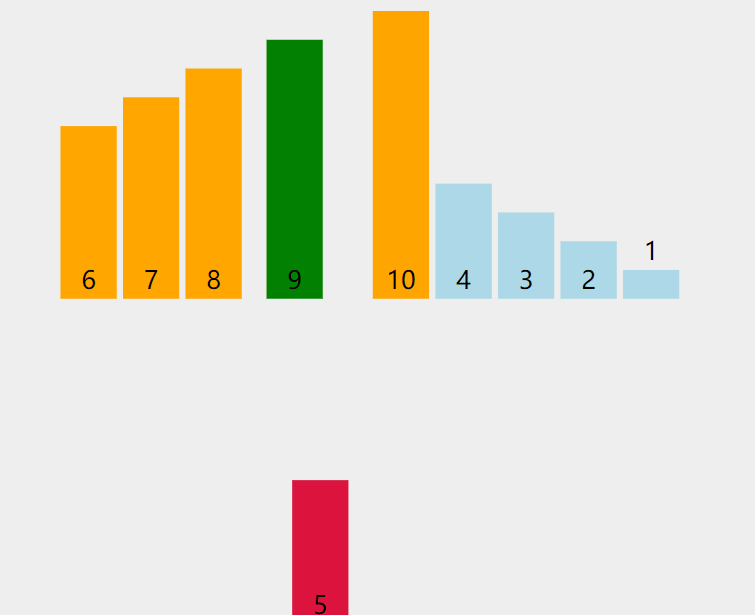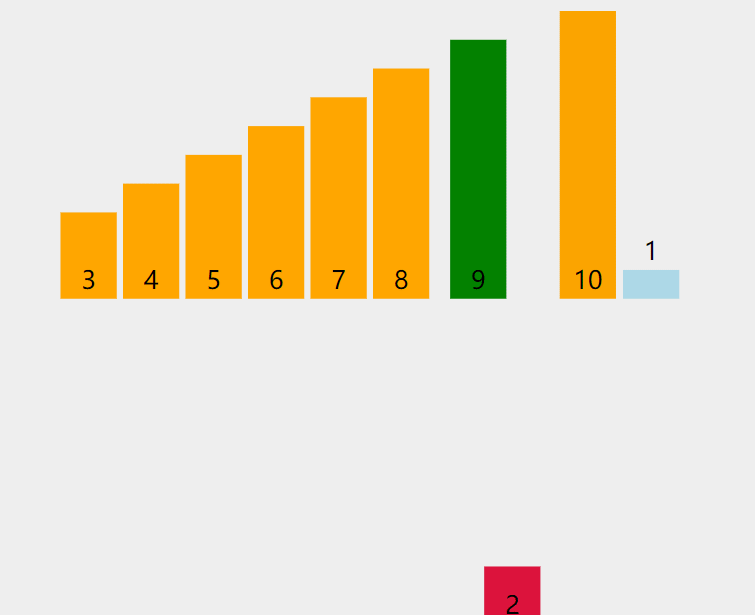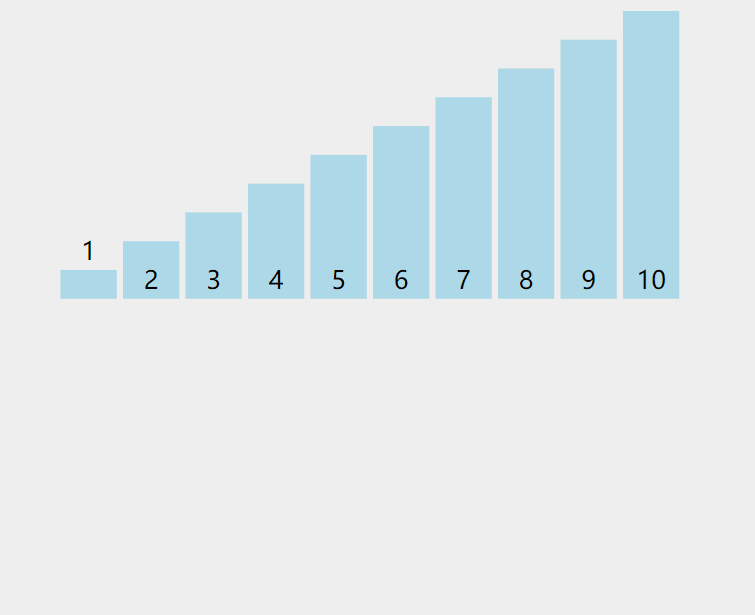
对于一个乱序序列arr，我们可以找到其已排好序列的末尾，定义其下表为end，再用变量tmp存下arr[end]后一位数据（我们规定，在一个数组arr中，arr[i + 1]为arr[i]的后一位数据）。

然后进入循环，我们假设排升序。当tmp < arr[end]时，arr[end]向后进一位，end--；当tmp >= arr[end]时，结束循环；当end前进到小于0时，也结束循环。

然后，将tmp存的值，放入此时end + 1的位置上。

c 复制代码 
//直接插入排序
void InsertSort(int* arr, int size)
{
	//排完倒数第二个数，就已经排完了
	for (int i = 0; i < (size - 1); i++)
	{
		//定义已经排好序列的末尾下标为end
		//由于每次for循环后，排好的序列中，元素个数+1，所以end == i
		int end = i;
		//存下arr[end]后一位的数据
		int tmp = arr[end+1];
		//遍历，arr[end]与tmp比较，需要前移时，end--
		while (end >= 0)
		{
			if (tmp < arr[end])//排升序：<    排降序：>
			{
				arr[end + 1] = arr[end];
				end--;
			}
			else {
				break;
			}
		}
		//跳出while循环，将tmp中数放下
		arr[end + 1] = tmp;
	}
}

对于直接插入排序排，我们假设要将一个降序序列，排成升序序列。

那么，当 i = 0 ，交换 0 次；当 i = 1 ，交换 1 次；当 i = 2 ，交换 2 次......当 i = (size - 2) ，交换 (size - 2) 次。

不难看出，直接插入排序（在最差情况下）时间复杂度，要小于O(N^2)。

这是在所有大的数据在前面，所有小的数据在后面；那么当小的数据在前面，大的数据在后面，是不是就简化了算法？

根据这一思路，我们来看希尔排序。

1.2、希尔排序

希尔排序是指，给定一个整数gap，将一组数据每隔相同间隔分一组，每组进行直接插入排序；然后每次将gap进行特殊处理（gap = gap / 3 + 1），再分组，每组进行直接插入排序......直到 gap == 1 ，也就是对所有数据进行直接插入排序。但是其时间复杂度，肯定比上来就直接插入排序的时间复杂度要低。

我们给出一个例子：

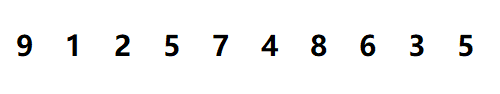
如图是一个乱序序列。元素个数为10。我们一开始先假设 gap = 5 ，那么分组情况、分组直插排序后结果如下图（这里我们每一种颜色的线连的数据为一组）：

不难看出，在排成升序序列的情况下， 排好一次后小的数据到了前面，大的数据到了后面。

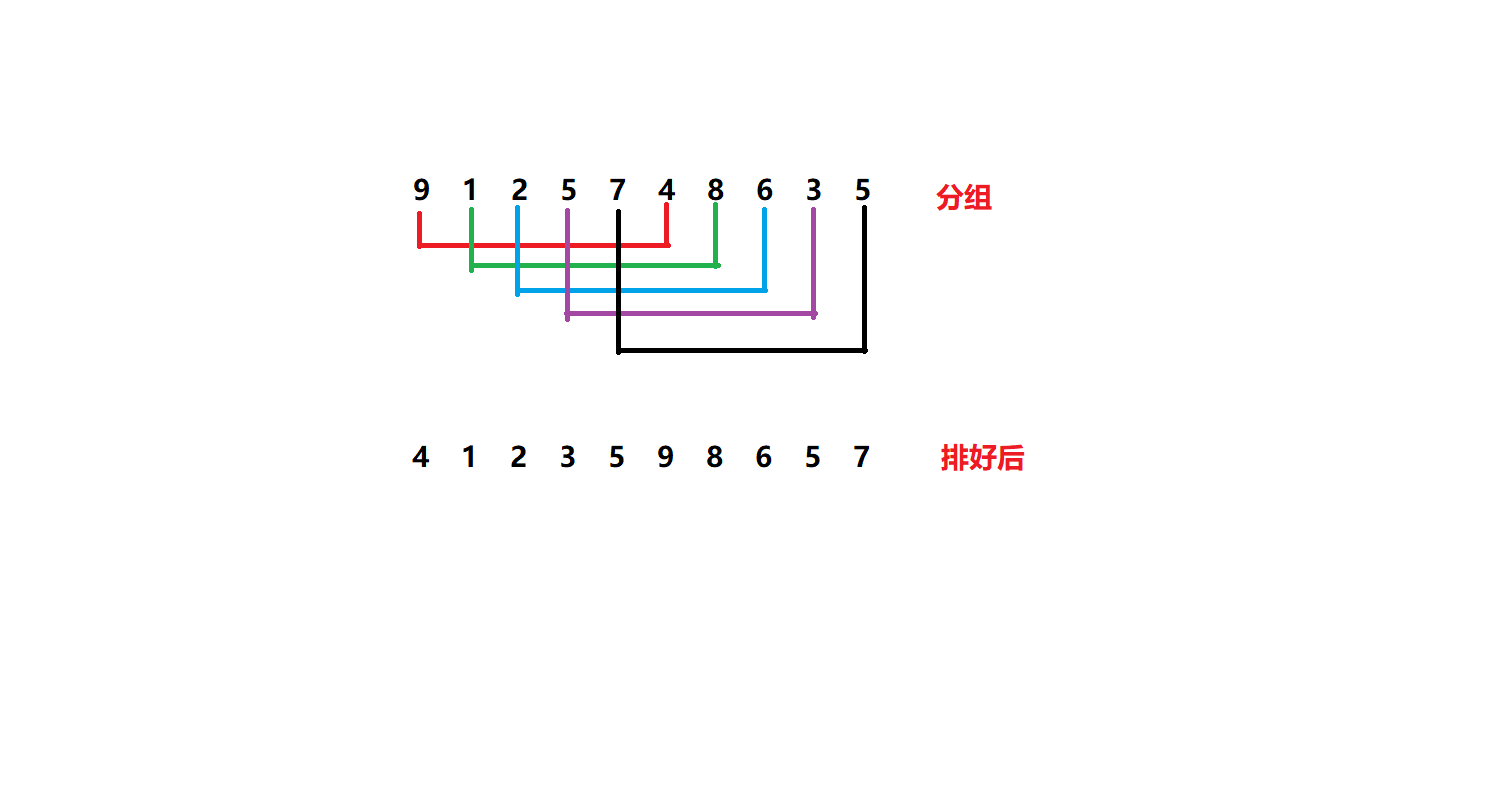
再来一次。这时，gap = 2 ：

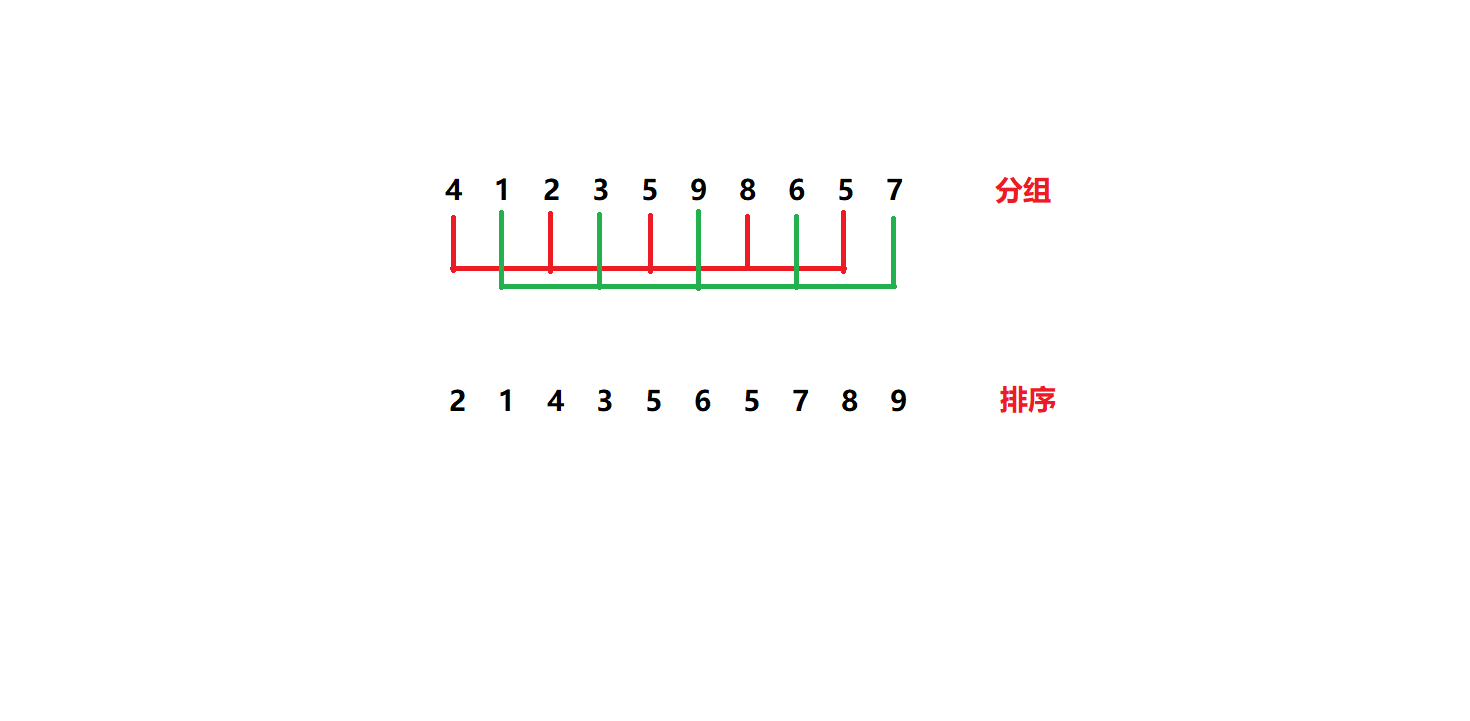
再来一次，此时gap = 1，相当于直接插入排序，结束。

c 复制代码 
void ShellSort(int* arr, int size)
{
	int gap = size;//gap从元素个数开始
	while (gap > 1)
	{
		gap = gap/3 + 1;//经过这个转换式，最后gap一定为1，此时进入循环，结束后完成升、降序排列，所以第一层循环判断条件：gap > 1
		for (int i = 0; i < size - gap; i++)//①//结合图理解i < size - gap；而i++可以做到直插排序每一组数据，也就不需要另外的循环
		{//下面的代码，可以理解为由每一个（直接插入）排序，到每隔gap个（直接插入）排序
			int end = i;
			int tmp = arr[end + gap];
			while (end >= 0)
			{
				if (arr[end] > tmp)
				{
					arr[end + gap] = arr[end];
					end -= gap;
				}else{
					break;
				}
			}
			arr[end + gap] = tmp;
		}
	}
}

对于①处代码，相当于用一行for (int i = 0; i < size - gap; i++)，代替了两行这样的代码：

那么希尔排序的时间复杂度，如何计算？

希尔排序的外层循环，由gap = gap/3 + 1，得外层循环的时间复杂度为O(logN)。

对于希尔排序的总过程，这里只能给出一个大概的、不准确的解释：

对于一组数据（m个数据），如果这组数据是降序的，要调整成升序，需要调整次数：
1 + 2 + 3 + ⋅ ⋅ ⋅ ⋅ ⋅ ⋅ + ( m − 2 ) + ( m − 1 ) 1+2+3+······+(m-2)+(m-1) 1+2+3+⋅⋅⋅⋅⋅⋅+(m−2)+(m−1)对于n个数据排成gap组，假设n/gap为整数，则每组有
n/gap 个数据，需要调整次数：
1 + 2 + 3 + ⋅ ⋅ ⋅ ⋅ ⋅ ⋅ + ( n / g a p − 2 ) + ( n / g a p − 1 ) 1+2+3+······+(n/gap-2)+(n/gap-1) 1+2+3+⋅⋅⋅⋅⋅⋅+(n/gap−2)+(n/gap−1)

而对于gap （组数）的取值，假设我们不是gap = gap/3 + 1，而是gap /= 3。那么gap的取值有：n/3、n/9、n/27······2、1

  • 当 gap = n/3 ，移动总数：(n/3)*(1 + 2) = n
  • 当 gap = n/9 ，移动总数：(n/9)*(1 + 2 + ··· + 8) = 4n
  • ······
  • 当 gap = 1 ，此时为直接插入排序，同时几乎所有小数据在左，大数据在右。我们假设通过许多次gap > 1 的排列后，当gap = 1，直接插入排序达到最好情况：n，也就是说，移动总数为：n

对于移动总数，这里存在一个n开始递增，然后在一个点递减，一直递减到n的过程。有的书籍上说，这个点对应的值，也就是希尔排序的时间复杂度，可能为n^(1.3)。

2、选择排序

2.1、直接选择排序

直接选择排序是指，在待排序的序列中，挑选 出最小或最大的数据，放入到序列开头。

我们还是以排升序为例。

比如有一段序列：

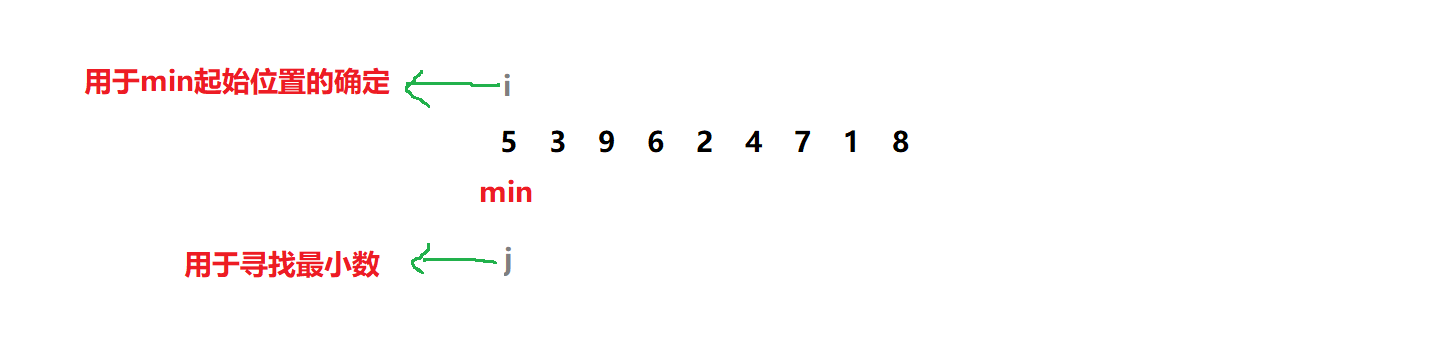
我们定义变量min。一开始所有数据都需要排序，所以min在数组首位 ；然后循环，使min定位 序列的最小数据；找到后，循环结束，进行交换 操作使最小数到序列最前方。

这时，for循环中，i不断加1，待排序列个数也不断减1，既然min在数组首位，那么每次i的循环执行时，min = i。

根据上面思路，写出代码：

c 复制代码 
//选择排序
void SelectSort(int* arr, int size)
{
	for (int i = 0; i < size; i++)
	{
		int min = i;
		for (int j = i; j < size; j++)
		{
			if (arr[j] < arr[min])
			{
				min = j;
			}
		}
		Swap(&arr[i], &arr[min]);//最小值与当前待排序列的首位进行交换
	}
}

我们来想一想有什么优化的方法。

在上面的代码，我们对于一段待排序序列，只是去找了它的最小值。那我们能不能既找最小值，又找最大值？

我们对于一段待排序列，可以定义变量begin标记待排序列的首位（下标），定义变量end标记待排序列的末位（下标）；然后，定义变量max寻找待排序列的最大值（下标），定义变量min寻找待排序列的最小值（下标）。

每次在begin+1与end中找最大值、最小值（max、min一开始定义在begin上，就没必要在begin上开始找），寻找完后最大值与end值交换，最小值与begin值交换，然后begin前进，end后退。

c 复制代码 
//选择排序改良版
void SelectSort(int* arr, int size)
{
	int begin = 0;
	int end = size - 1;
	while (begin < end)
	{
		int max = begin;
		int min = begin;
		for (int i = begin+1; i <= end; i++)
		{
			if (arr[i] < arr[min])
			{
				min = i;
			}
			if (arr[i] > arr[max])
			{
				max = i;
			}
		}
		Swap(&arr[begin], &arr[min]);
		Swap(&arr[end], &arr[max]);
		
		begin++;//执行操作一定要写
		end--;
	}
}

代码初步建成，但是我们试图用这段代码，去排序一开始的示例序列时，出现了这样一个问题：

我们发现，6和4的位置不对。为什么会这样？

画图走几步看看。

我们发现走到这一步时，max恰好在begin上，min恰好在end上。如果我们直接进行交换，那么交换两次之后，相当于没交换。

当我们碰到这种max恰好在begin上，min恰好在end上的情况时，我们不妨让max或min的其中一个待在另一个上，在交换。这样真正的交换只有一次，而另一次交换是自己与自己交换。

c 复制代码 
//再改良版
void SelectSort(int* arr, int size)
{
	int begin = 0;
	int end = size - 1;
	while (begin < end)
	{
		int max = begin;
		int min = begin;
		for (int i = begin + 1; i <= end; i++)
		{
			if (arr[i] < arr[min])
			{
				min = i;
			}
			if (arr[i] > arr[max])
			{
				max = i;
			}
		}
		if (min == end && max == begin)//改了这里
		{
			max = min;
		}
		Swap(&arr[begin], &arr[min]);
		Swap(&arr[end], &arr[max]);

		begin++;//执行操作一定要写
		end--;
	}
}

那么对于直接选择排序，无论改不改良，时间复杂度都为O(N^2) （比O(N^2)略微要小）。

(终于可以表示上标2*(n-1)了！！！！！)

2.2、堆排序

堆排序在前面已经实现过了。其主要过程就是：

  1. 向下排序算法整理成堆
  2. 首尾交换
  3. 排除尾，剩余的向下排序算法整理成堆
c 复制代码 
//向下调整算法
void AdjustDown(int* arr, int parent, int size)
{
	//找孩子
	int child = parent * 2 + 1;
	while (child < size)//防止孩子越界
	{
		//假设排升序，那么建大堆
		//找大孩子
		if (child + 1 < size && arr[child+1] > arr[child])
		{
			child++;
		}
		//比较父子
		if (arr[child] > arr[parent])
		{
			Swap(&arr[child], &arr[parent]);
		}else{
			break;//由于这个算法是在只有指定父节点不满足堆数据结构的要求的情况下，
			//执行的调整算法，
			//故向下时如果没到最下面的节点就满足了堆要求，就直接结束
		}
		parent = child;
		child = child * 2 + 1;
	}
}

//堆排序
void HeapSort(int* arr, int size)
{
	//向下调整算法，调整成（大）堆
	for (int i = (size - 1 - 1)/2; i >= 0; i--)//从大到小
	{
		AdjustDown(arr, i, size);//每次从i开始
	}
	
	int end = size - 1;
	while (end > 0)//排到剩下两个数，已经排好了
	{
		Swap(&arr[0], &arr[end]);
		AdjustDown(arr, 0, end);
		end--;
	}
}

3、交换排序

3.1、冒泡排序

冒泡排序，我们在C语言的学习中，就已经见识过了。就是规定趟数，每趟比较交换：

c 复制代码 
void BubbleSort(int* arr, int size)
{
	for (int i = 0; i < size - 1; i++)
	{
		int flag = 1;//标记，防止排好了还要排
		for (int j = 0; j < size - 1 - i; j++)
		{
			if (arr[j] > arr[j+1])
			{
				flag = 0;
				Swap(&arr[j], &arr[j+1]);
			}
		}
		if (flag)
			break;
	}
}

3.2、快速排序

我们之前学习了C语言内置的快速排序qsort()，以及如何用冒泡排序的思想去实现快速排序。

今天我们学点不一样的。

我们今天学的快速排序，借助了二叉树结构。

比如这里有一个序列：

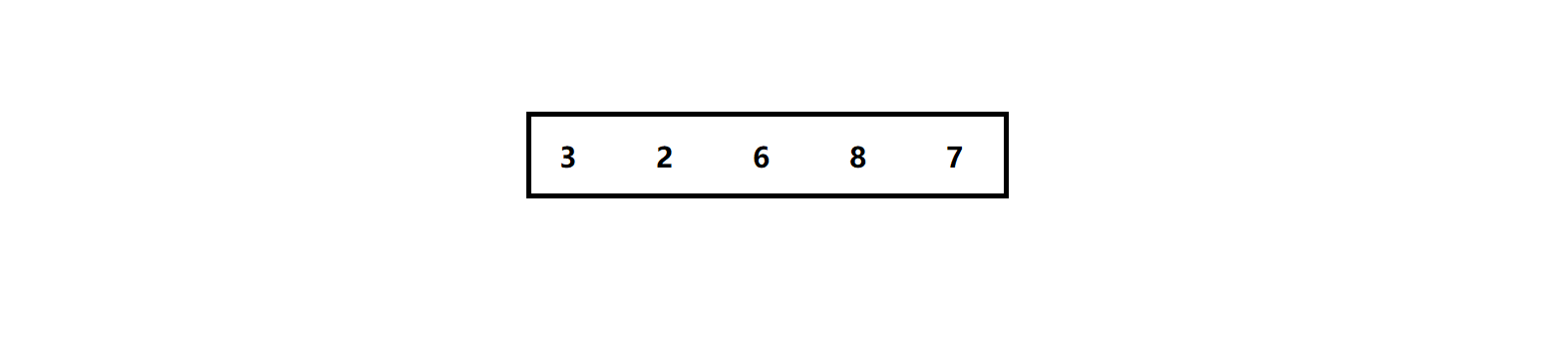
假设我们排升序

我们以6 作为基准值，将小于6的值放入6的左边，大于6的值放入6的右边，从而将这个序列分为两个更短的子序列：

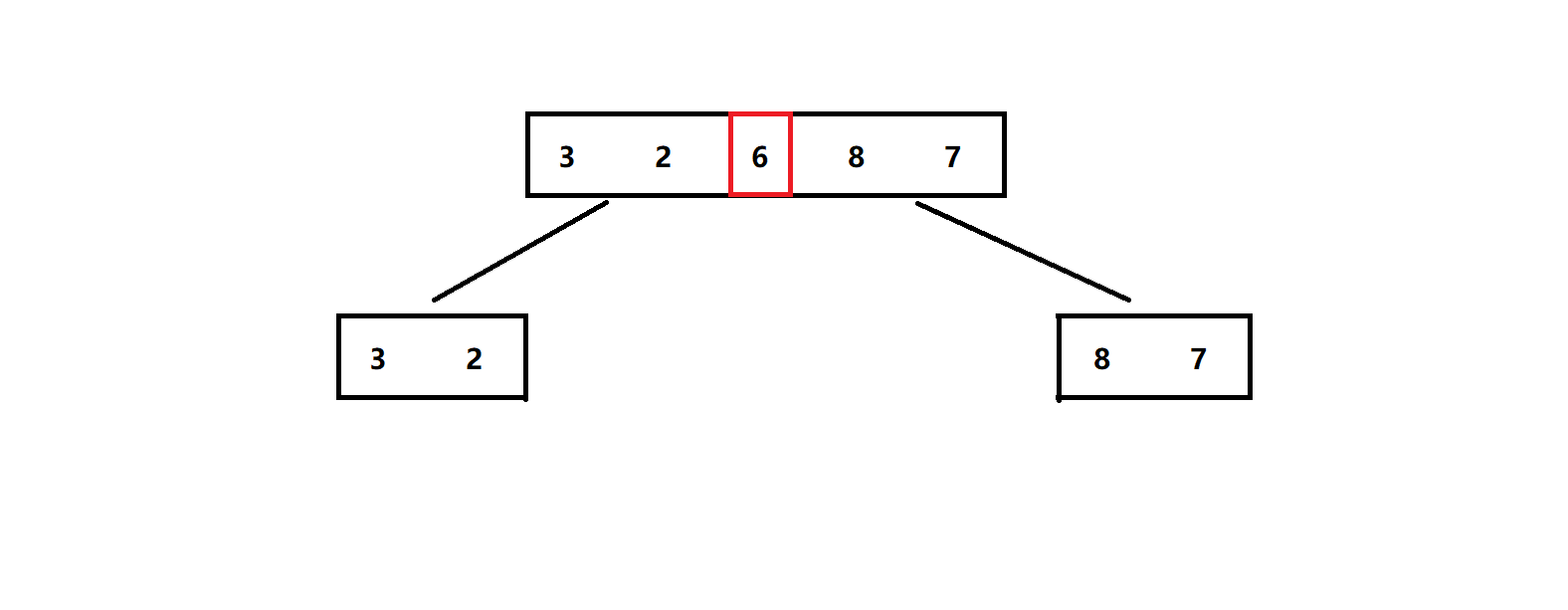
至于怎么放数据，我们之后会讲。

当我们得到子序列，我们就对子序列重复操作：

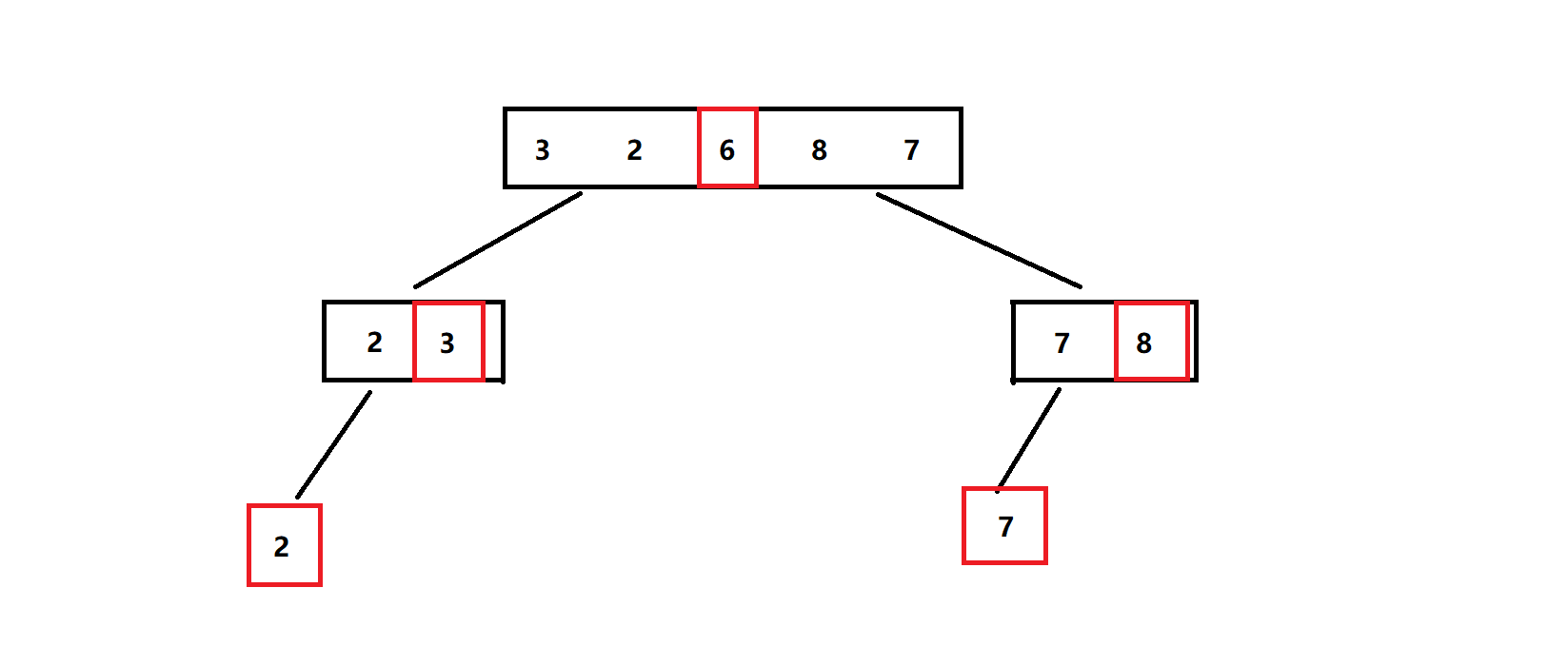
那么最后我们将得到一个升序序列。

此时，我们不难想到这里需要用递归来实现，所以我们可以设计出快速排序的基本框架：

c 复制代码 
void QuickSort(int* arr, int left, int right)
{
	if (left >= right)
	{
		return;
	}
	//key
	//TODO
	QuickSort(arr, left, key - 1);
	QuickSort(arr, key + 1, right);
}

在这里我们并不是简单的传入数组元素个数，而是传入数组的最左端下标left 和最右端下标right。

那么问题来了，我们如何找到基准值？又或者说，我们如何找到基准值、将基准值放入合适的位置、调整数组（小于基准值的数据全在基准值左侧，大于基准值的数据全在基准值右侧）？

3.2.1、hoare方法

我们再来看到一个序列：

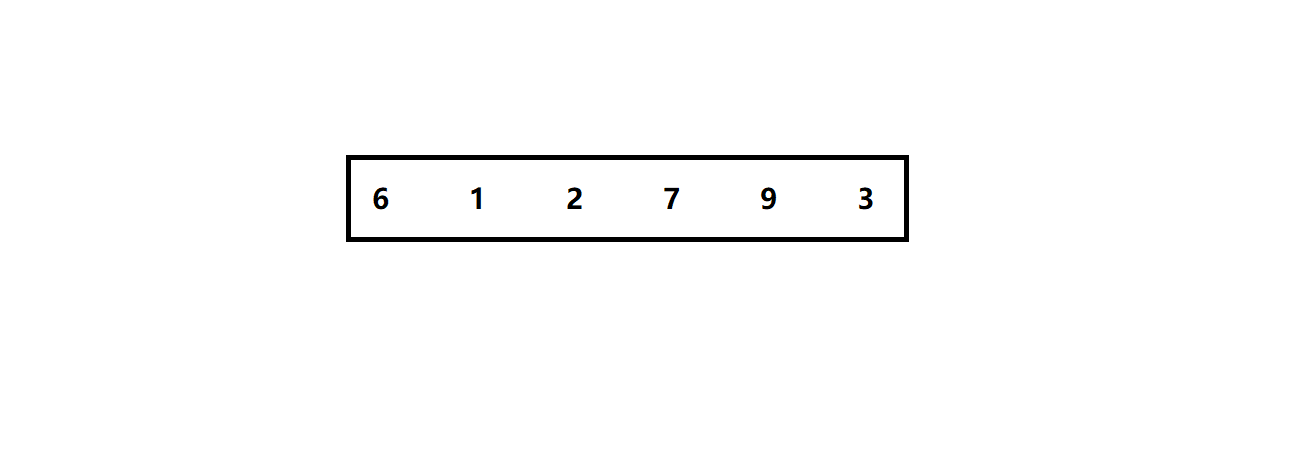
我们需要三个变量：

  1. key：基准值的下标
  2. left：数组最左端下标
  3. right：数组最右端下标

同时，我们规定：单词本身是下标（left），单词带i是下标对应的数（lefti）

先将这三个下标变量放到数组中：

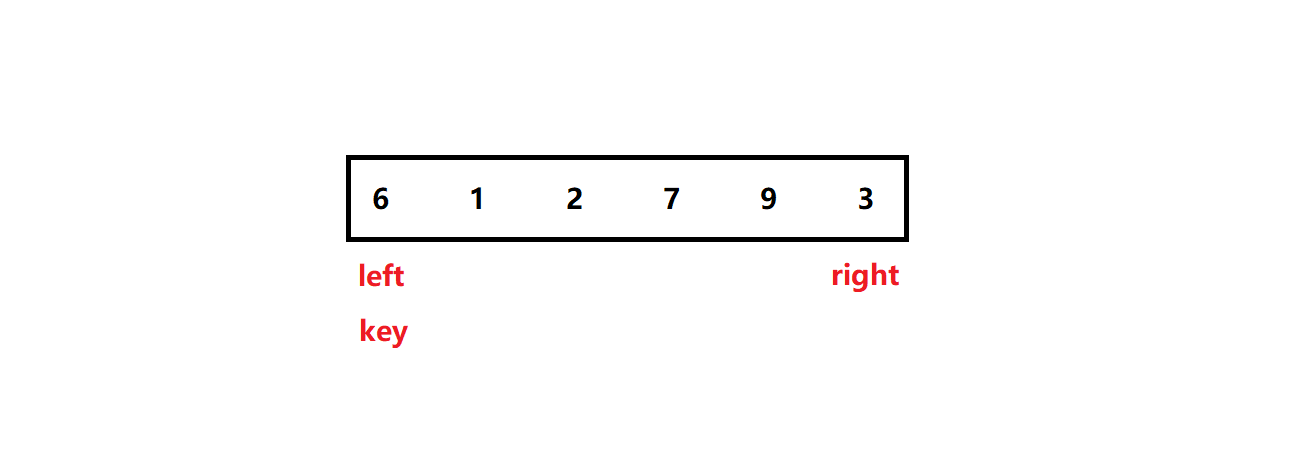
接下来，我们做两件事：

  • right：从右往左，不小于left，找小于基准值的数，为后面放入基准值左侧做准备
  • left：从左往右，不大于right，找大于基准值的数，为后面放入基准值右侧做准备

当然，本身比较没必要，所以left可以前进一位。

当left和right都找到了符合要求的数，在left <= right 的情况下，交换数据，也就做到了小于基准值的数据全在基准值左侧，大于基准值的数据全在基准值右侧。

当left > right ，keyi 与righti交换，返回正确位置right。

c 复制代码 
int _QuickSort1(int* arr, int left, int right)
{
	int key = left;
	left++;
	while (left <= right)//①
	{
		//④
		//right从右往左，不小于left，找小
		//升序：>    降序：<
		while (left <= right && arr[right] > arr[key])
		{
			--right;
		}
		//left从左往右，不大于right，找大
		//升序：<    降序：>
		while (left <= right && arr[left] < arr[key])//②
		{
			++left;
		}
		if (left <= right)
		{
			Swap(&arr[left++], &arr[right--]);//③
		}
	}
	Swap(&arr[key], &arr[right]);
	return right;
}
3.2.1.1、几个地方的理解
3.2.1.1.1、时间复杂度

这个快速排序的时间复杂度，为多少呢？

我们看到找基准值的函数，虽然有循环嵌套，但是不难看出，都是对同一个数组 的left++、right--，所以这个函数的时间复杂度为O(N)。

那么对于"框架"函数，由于每次分出子序列的操作好像"对半砍"，所以时间复杂度为O(logn)。

那么整个快速排序的时间复杂度，为O(NlogN)。

然而对于"框架"函数，当待排序列有序 或基准值选择不合适 ，即分出的其中一个子序列元素很多，另一个子序列元素很少，此时"框架"函数的时间复杂度近似为O(N) ，就导致整个快排函数的时间复杂度近似O(N^2)。

3.2.1.1.2、while (left <= right)

在标记①处。

我们知道，最后是要将keyi 与righti 交换，并返回right 。此时right至关重要。

当left与right重合，即left == right 时，如果right的不符合要求，那么我们就再一次进入循环，使得right找到合适的位置 。所以我们循环的条件为left <= right。

3.2.1.1.3、arr[right] > arr[key]

在标记②处。

为什么不添加**=**？

如果我们加上**=，当待排序列中有许多 与基准数相等**的数，甚至所有数都与基准数相等时，对于这篇文章的代码，当走到right的调整循环中时，循环会不停执行，直到right越界：

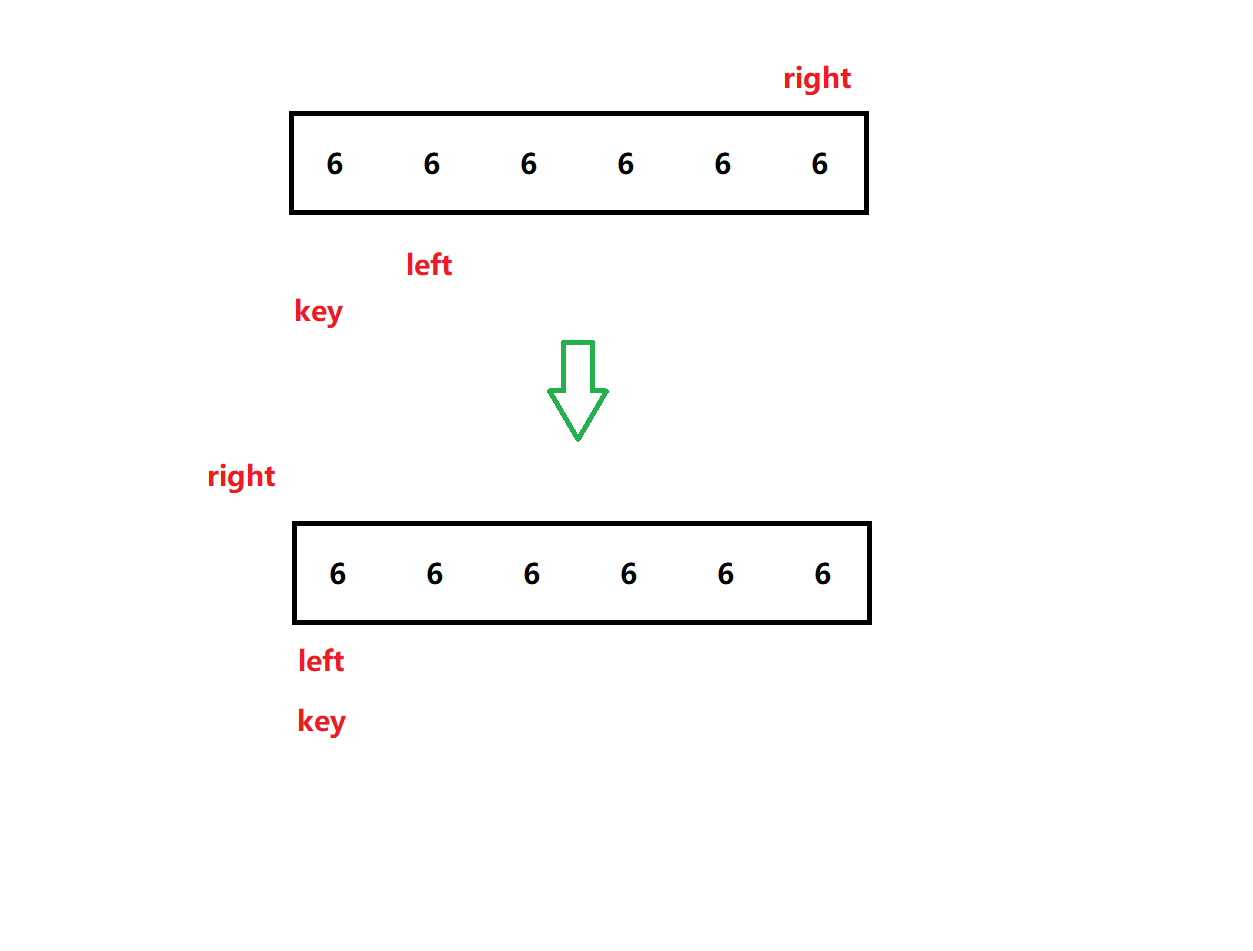
此时"框架"函数的时间复杂度也会变为O(N)。

所以不添加**=**。

3.2.1.1.4、Swap(&arr[left++], &arr[right--])

在标记③处。

为什么要left++ 、right--？

当left与right重合，即left == right 时，如果重复处对应的值与基准值相等 ，如果我们直接交换而没有让left++ 、right-- ，此时left == right ，进入循环，自然而然就变成死循环了。

所以必须left++ 、right--。

同时，这一处代码上面的if语句的存在，是为了防止将基准值以外的数扔错位置。

3.2.1.1.5、right 必须要先比 left 进行

在标记④处。

这里我们只要记住一点：基准值最好取序列的最左端，此时 right 先比 left 进行

3.2.2、挖坑法

以升序为例。

我们给到一个序列：

在这个序列中，我们依然定义数组的左右两端left 、right ，定义接收基准值的变量keyi。

然而，我们再定义一个变量hole 。我们先将hole放在数组的最左侧，即left位置处，然后在hole处挖一个坑 ，将此时的6作为基准值：

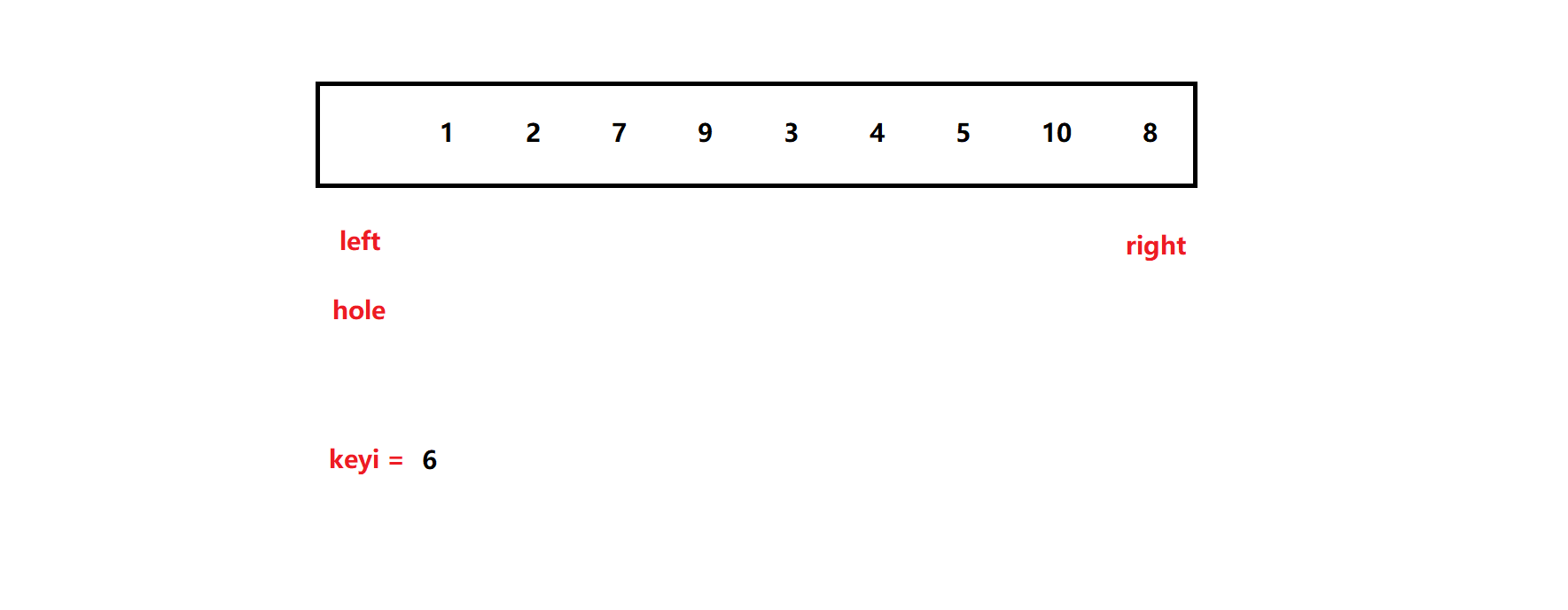
这时，right 与之前的hoare方法一样，向左找比基准值小的数，然后填坑 （赋值）：

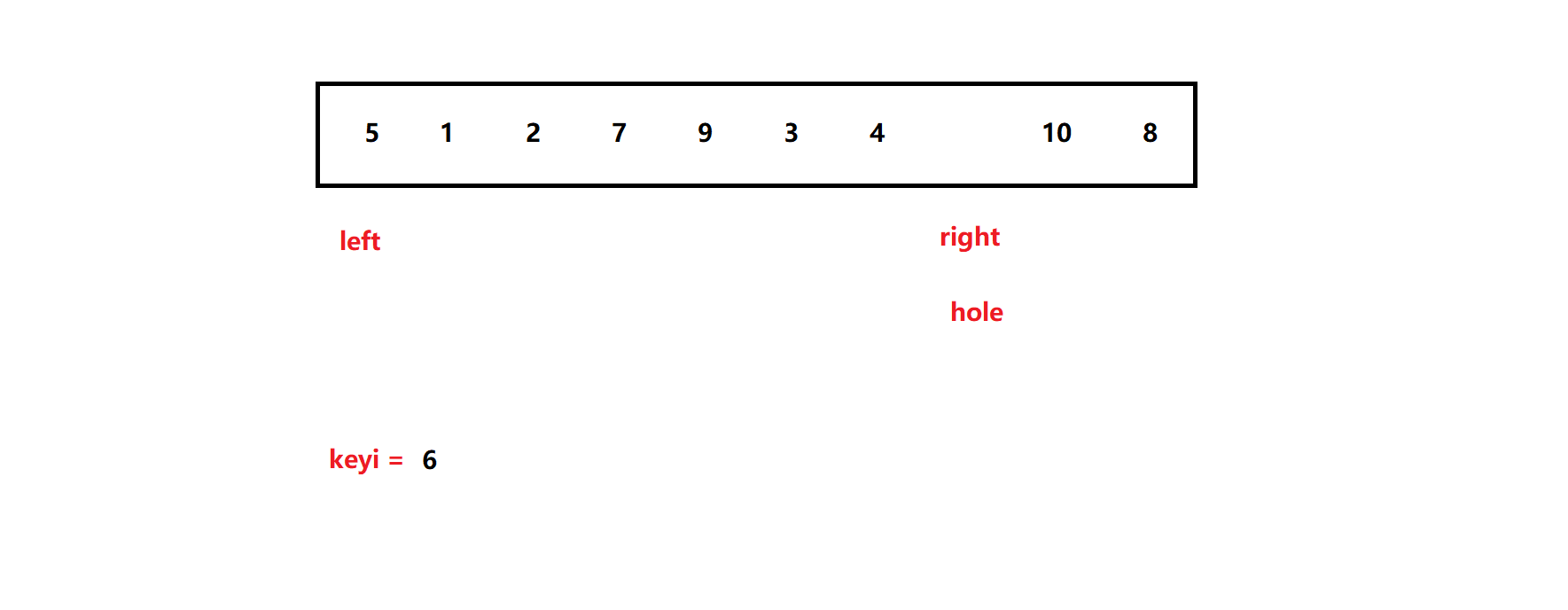
接着，left 向右找比基准值大的数，填坑 ：

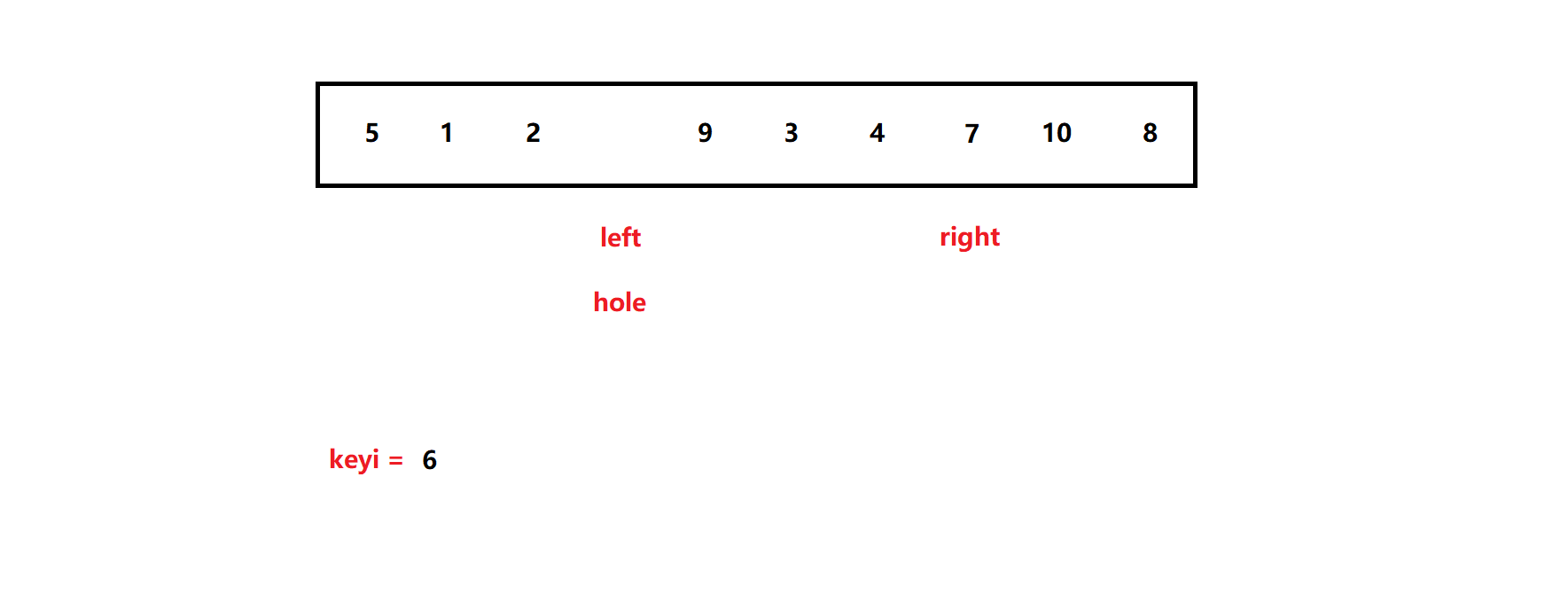
如此，left 与right 重复操作，直到left == right ：

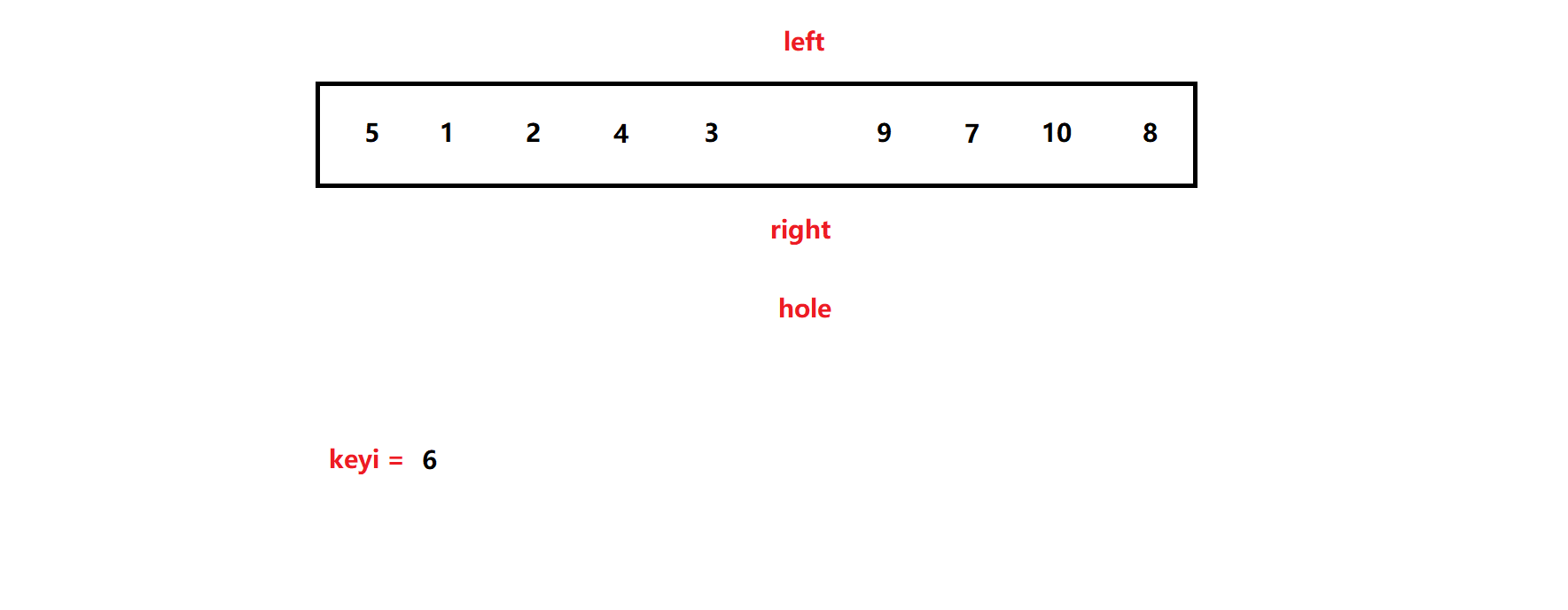
此时，结束（循环）操作，将keyi 填入坑中，完成。

c 复制代码 
int _QuickSort2(int* arr, int left, int right)
{
	int hole = left;
	int keyi = arr[hole];
	while (left < right)
	{
		//right向左找比基准值小的数
		while (left < right && arr[right] > keyi)
		{
			--right;
		}
		//找到了，填坑
		arr[hole] = arr[right];
		//坑转移
		hole = right;
		//left向右找比基准值大的数
		while (left < right && arr[left] < keyi)
		{
			++left;
		}
		arr[hole] = arr[left];
		hole = left;
	}
	//跳出循环后，赋值，返回位置
	arr[hole] = keyi;
	return hole;
}

3.2.3、lomuto前后指针法

这种方法，有点像我们之前学过的双指针法。

还是以升序为例，继续给到这个序列：

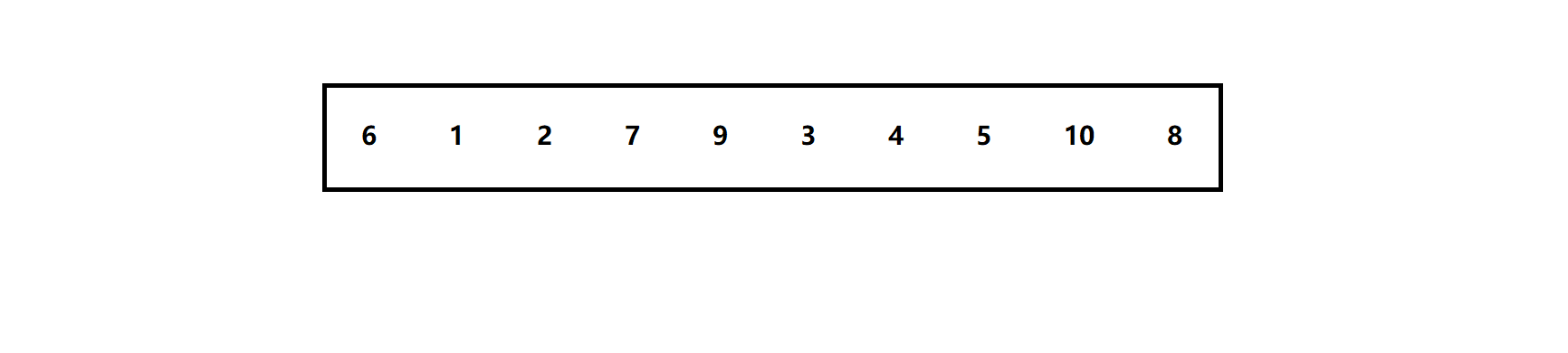
定义基准值下标key ，接着定义下标prev 、cur ，位置如图所示：

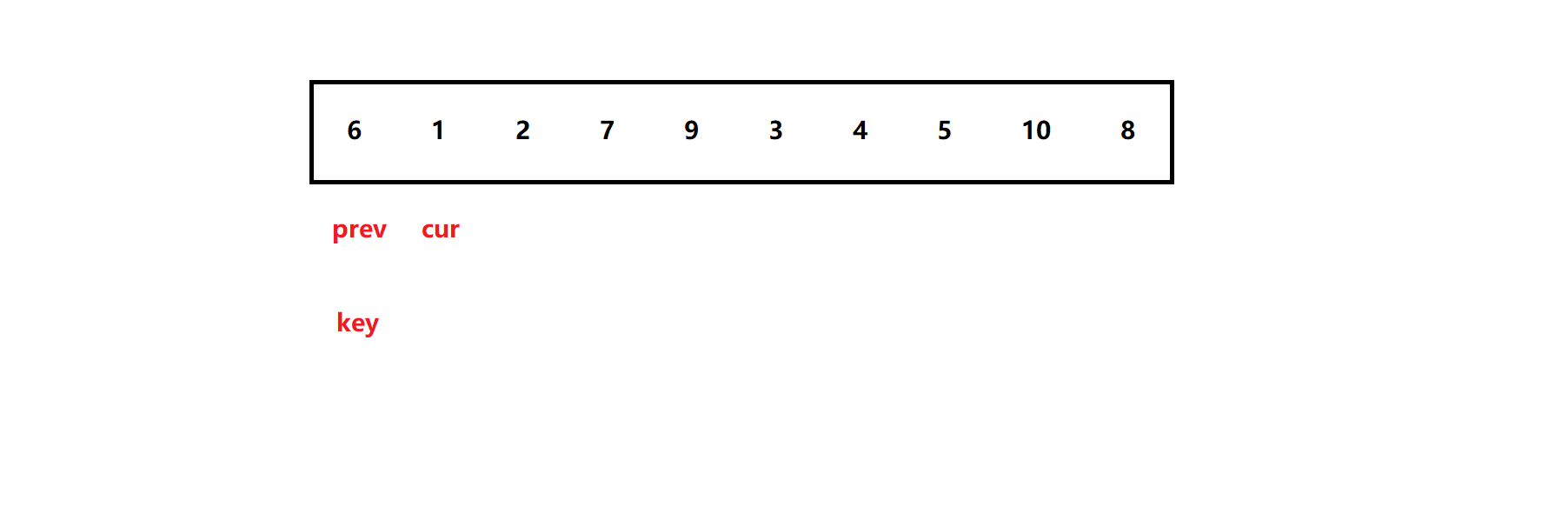
这时我们这样操作：

  1. 当cur指向的值小于基准值时，prev++，previ与curi交换，然后cur++
  2. 当cur指向的值不小于基准值时，直接cur++

当cur越界时，（循环）操作结束，prev的位置就是基准值的合适位置，然后交换，返回值：

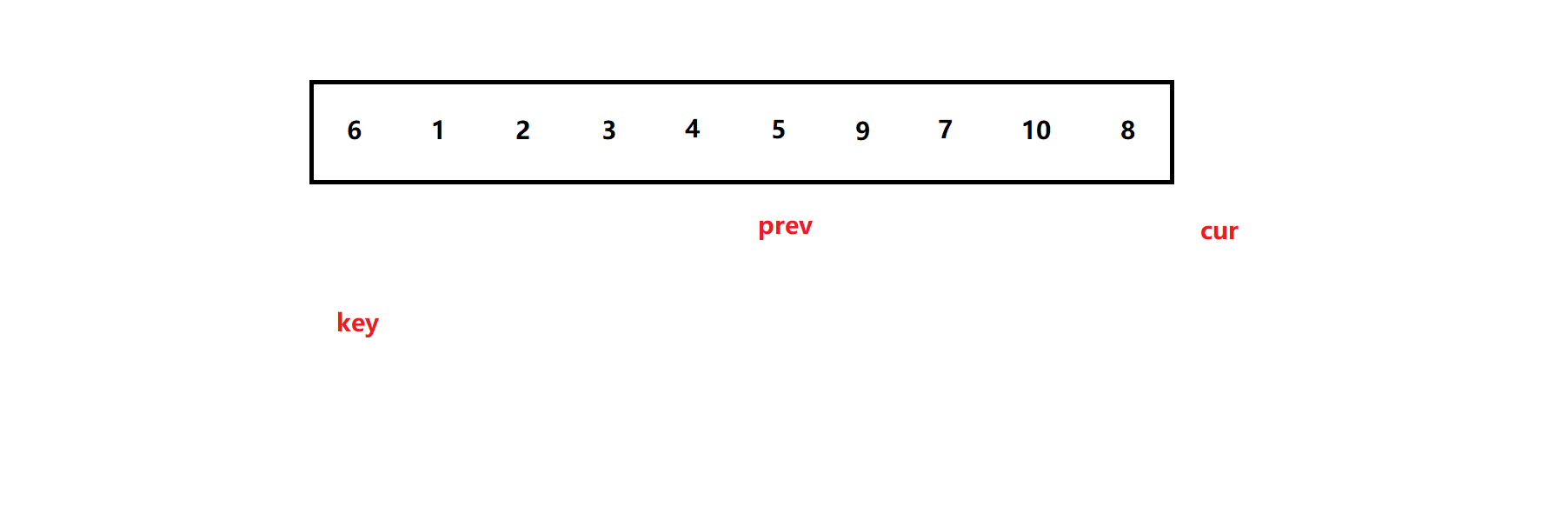
同时，为了防止prev + 1 == cur时，prev++后出现自己与自己交换，可以作判断优化。

c 复制代码 
int _QuickSort3(int* arr, int left, int right)
{
	int prev = left, cur = prev + 1;
	int key = left;
	while (cur <= right)
	{
		if (arr[cur] < arr[key] && ++prev != cur)
		{
			Swap(&arr[prev], &arr[cur]);
		}
		cur++;
	}
	Swap(&arr[key], &arr[prev]);
	return prev;
}

3.2.4、非递归的办法

（听说有的面试官会这样考！！！）

我们在递归方法中学到的思路，主要是两步：

  1. 搭框架，即确定排完当前范围的序列，继续排基准值左、右两个子序列的方向
  2. 找基准值。在这一步中，我们不仅为基准值（其实就是刚开始的序列首元素）找到了合适的方向，而且将小于基准值的数，和大于基准值的数，分别放入了基准值的左右两侧。

在非递归方法中，我们找基准值的思路是和递归方法的一样，问题是搭框架思路的替换。

我们给出一个序列，使用lomuto法演示找基准值的过程，并给出数组下标：

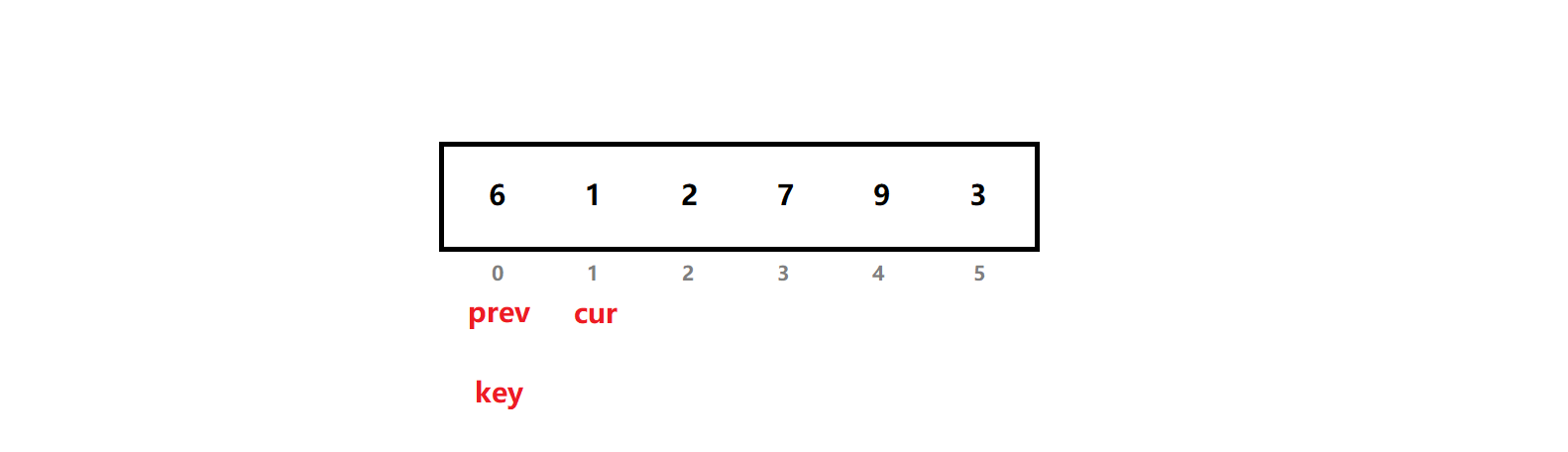
我们直接跳到找到基准值位置，调整序列的一步：

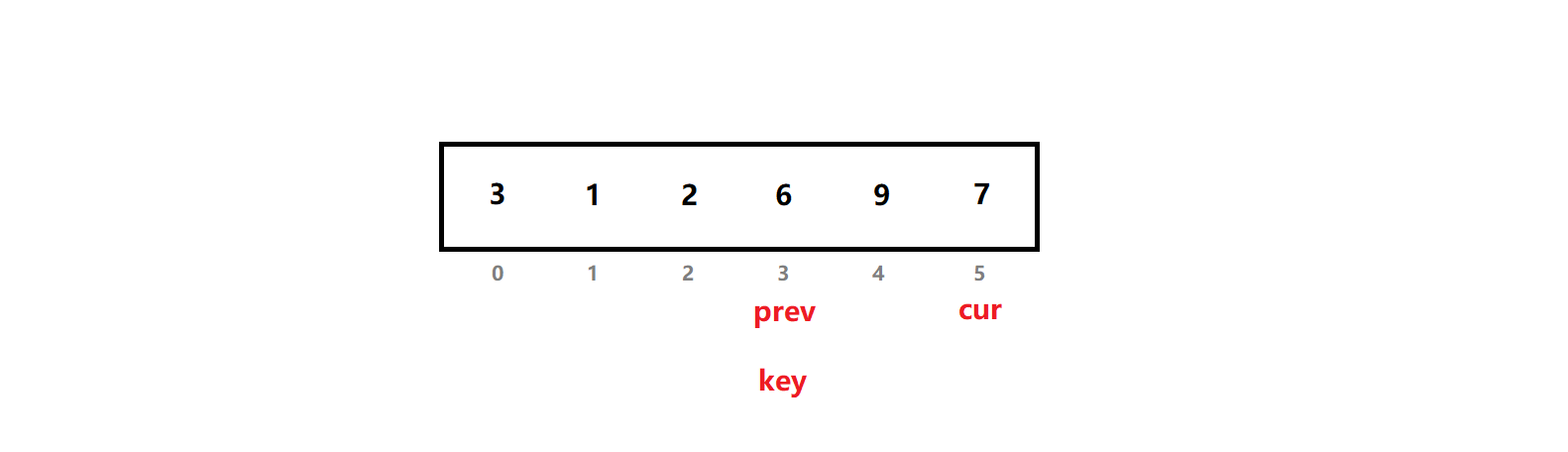
为了方便理解，基准值下表key 也放到了prev处。

这时，以基准值为界，分成左右两个子序列：

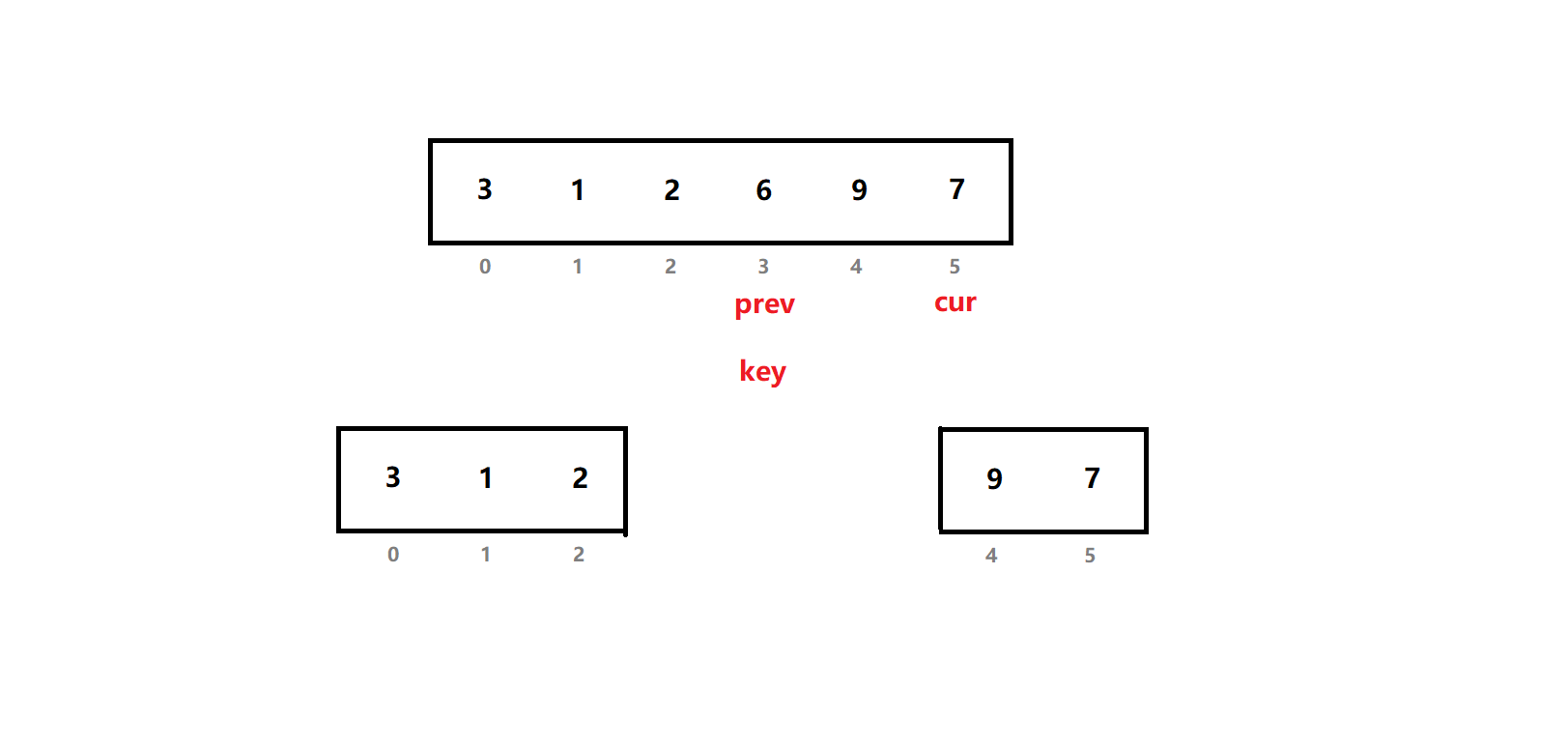
在递归方法中，我们可以接着调用函数，输入子序列的左右端进行排序。

那么在非递归方法 中，当我们完成了找基准值（位置）之后，我们也要得到子序列的左右端，并且继续进行找基准值 的操作。那么这时，我们可以借助数据结构栈。

首先，我们将序列的左、右端下标入栈 ，使得栈不为空 ：

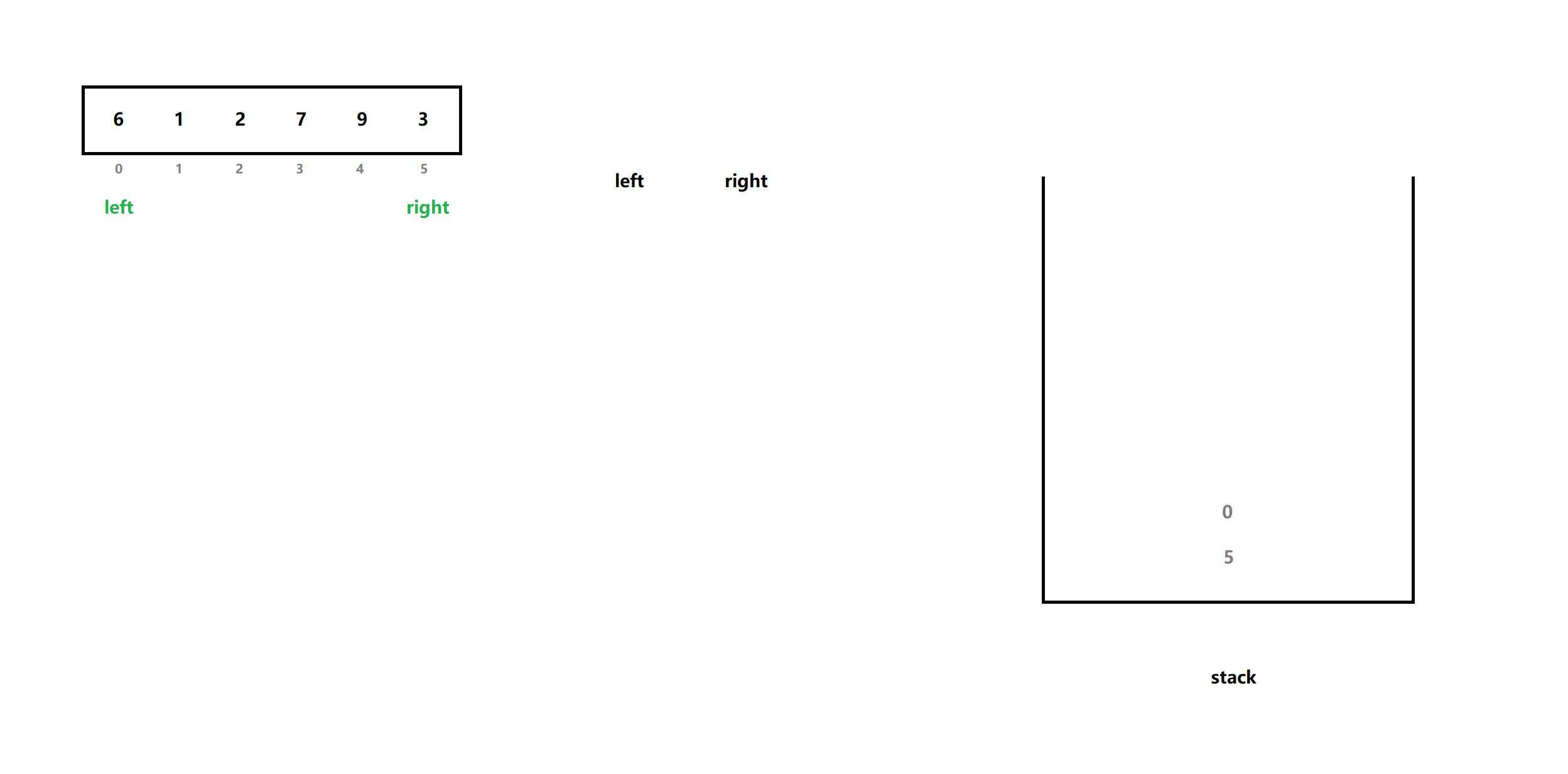
然后进行两次取栈顶，出栈 ，得到当前范围的待排序列的左、右端：

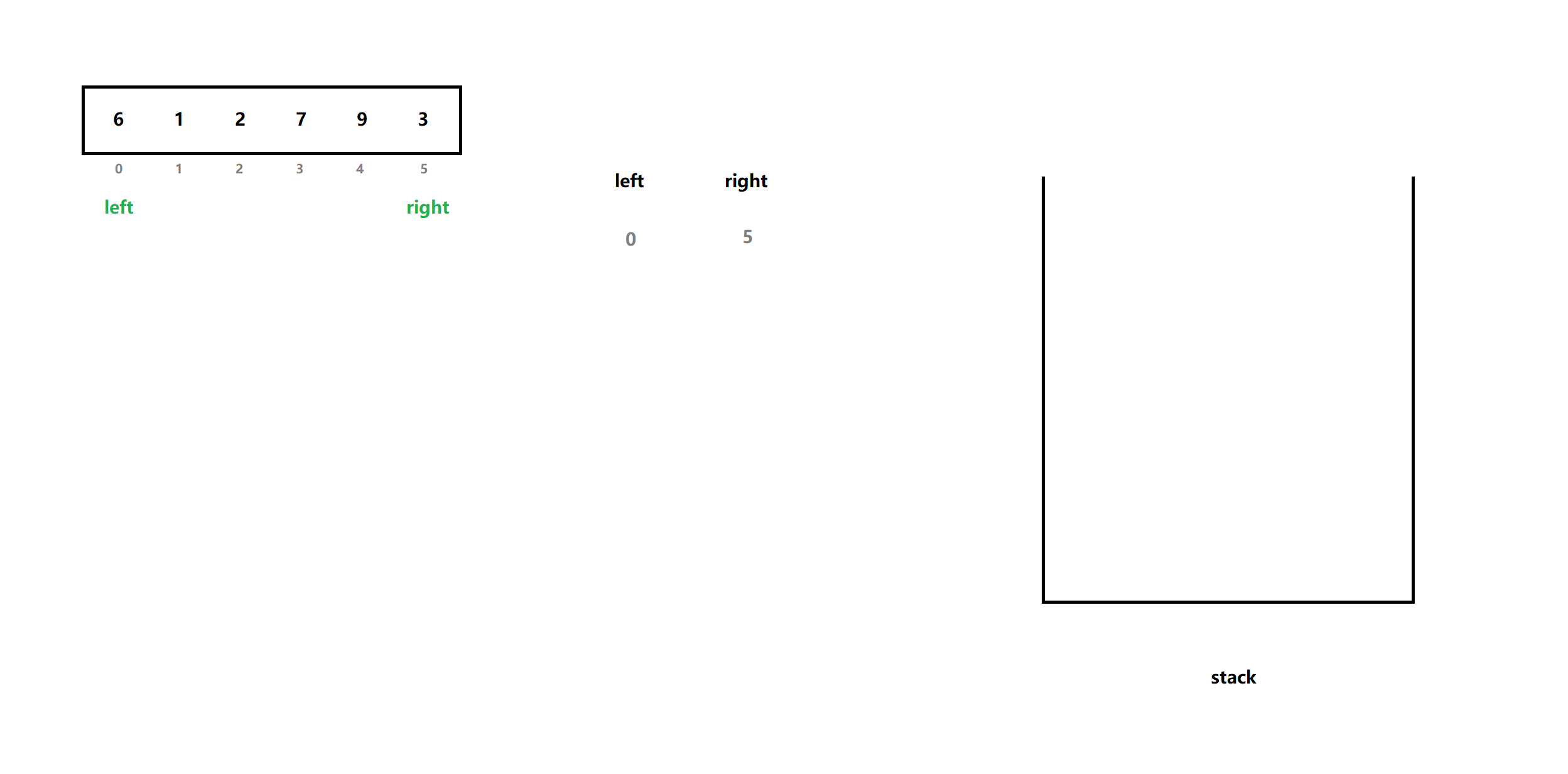
接着用这两端，进行找基准值 操作，得到基准值下标key ，此时分出左、右序列：

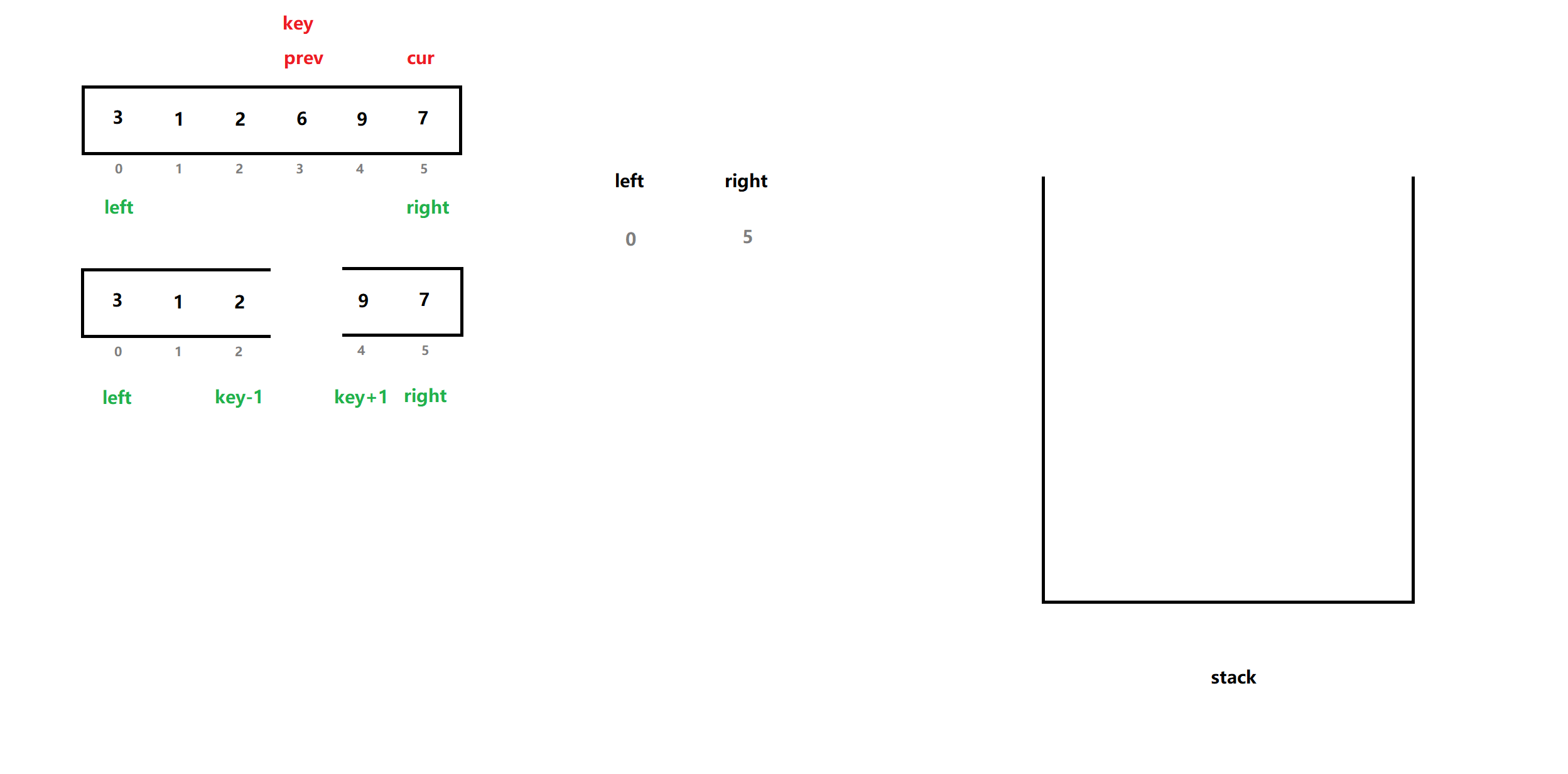
此时我们在入栈前，需判断此时的两个子序列是否有继续调整的必要。两种情况下子序列不能（不需要）调整：

  1. 子序列只剩下一个元素（left + 1 == key），不需要调整
  2. 子序列不存在（left + 1 > key），不能调整

判断没有问题时，我们入栈：

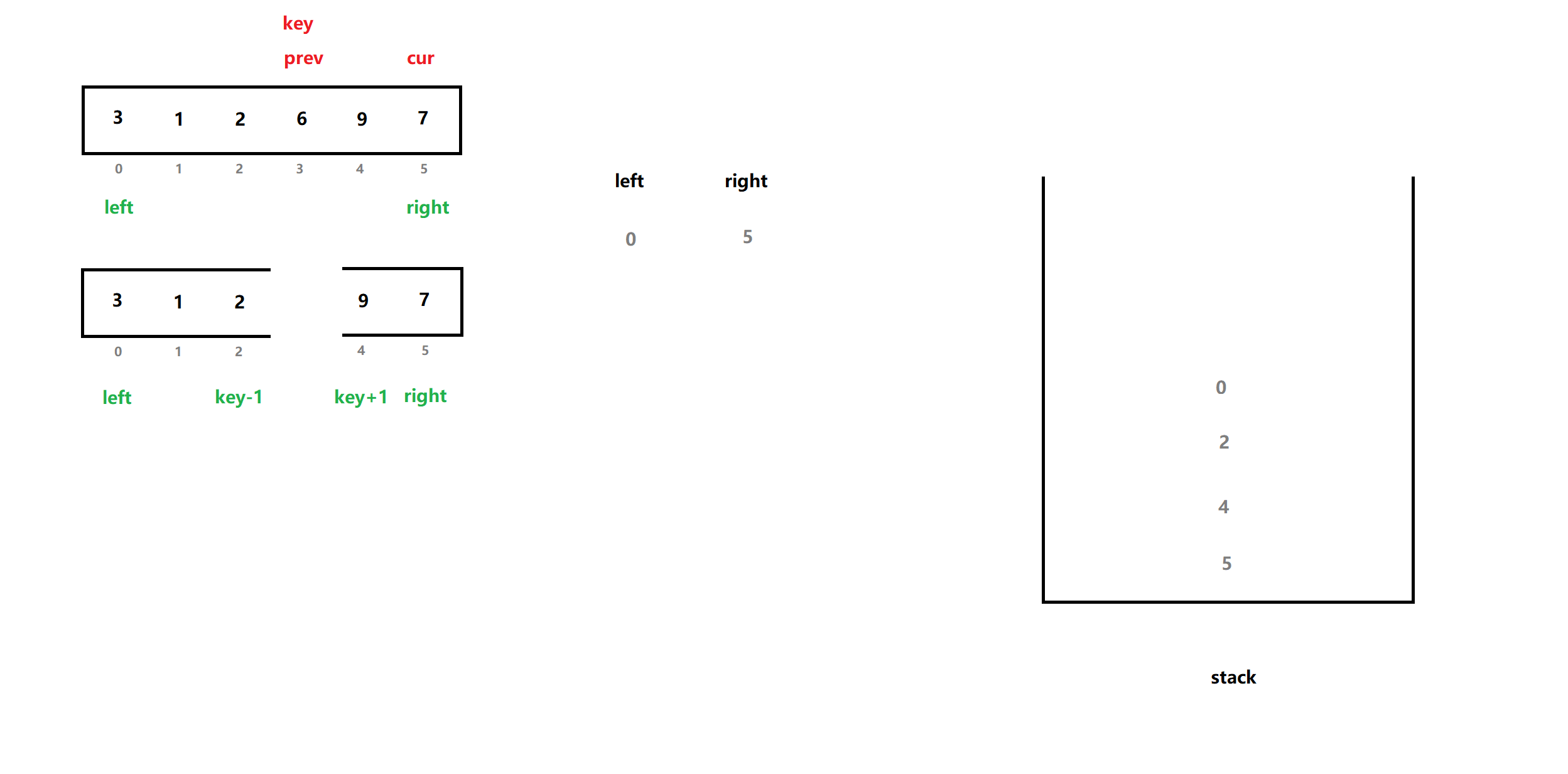
接着，我们再重复以上操作：进行两次取栈顶，出栈 、找基准值 ......直到栈为空。

所有的代码

相关推荐
5008432 分钟前
鸿蒙 Flutter 国密算法应用：SM4 加密存储与数据传输
分布式·算法·flutter·华为·wpf·开源鸿蒙
程序员-King.34 分钟前
day120—二分查找—统计公平数对的数目（LeetCode-2563）
算法·leetcode·二分查找·双指针
Yupureki36 分钟前
《算法竞赛从入门到国奖》算法基础:入门篇-枚举
c语言·数据结构·c++·算法·visual studio
雨季66638 分钟前
蓝桥杯试题及详解文档：统计子矩阵的和等于目标值的数量
算法
子夜江寒42 分钟前
线性回归与KNN算法的核心原理及实践应用
算法·回归·线性回归
MicroTech202543 分钟前
微算法科技（NASDAQ MLGO）采用混合深度学习赋能区块链：打造智慧城市安全新范式
科技·深度学习·算法
Yupureki1 小时前
《算法竞赛从入门到国奖》算法基础:入门篇-前缀和
c语言·数据结构·c++·算法·1024程序员节
啊吧怪不啊吧1 小时前
算法王冠上的明珠——动态规划之路径问题(第一篇）
大数据·算法·贪心算法·动态规划
青铜发条1 小时前
【算法】常见校验算法对比
算法·信息与通信·校验
热门推荐
01GitHub 镜像站点02【AutoGLM部署】本地私有化部署AI手机Agent03【超详细教程】手把手教你从微软官网免费下载Windows 10官方原版ISO镜像（2025最新版）04UV安装并设置国内源05安娜的档案(Anna’s Archive) 镜像网站/国内最新可访问入口（持续更新）06Open-AutoGLM Windows 安装部署教程07Linux下V2Ray安装配置指南08BongoCat - 跨平台键盘猫动画工具09React CVE-2025-55182漏洞排查与修复指南10在VSCode配置Java开发环境的保姆级教程（适配各类AI编程IDE）