对于高博的《视觉SLAM十四讲》一书中习题所涉及的一些算法的优化与比较，我看到文中并没有太多的量化处理方法，但是又在习题里面有提到，所以在此单独写一个博客来量化比较一下各种算法所带来的性能。这是一篇比较随意的博文，想到哪就写到哪，有问题就尝试然后观测实验结果。
1.数据集搭建
书中第七章的数据是两帧带有深度的图像数据，但是由于没有groundtruth真实坐标变换数值，所以没办法对算法进行量化评估，第八章LK算法使用了一段数据集freburg1_desk的图像，所以为了方便起见，本次也将使用freburg1_desk数据集中的数据。数据集下载：https://vision.in.tum.de/data/datasets/rgbd-dataset/download
数据集下载完成后就如同书中的方法一样，我们需要构建一个txt文件来引导我们的工程来循环读取数据集中的信息。和文中不一样的的是，这次在txt文件中还需要将groundtruth信息添加进去。工具依旧是associate.py，将这个python文件放入下载完成的rgbd_dataset_freiburg1_desk文件夹中，用终端打开这个数据集合文件夹，可以看到用于储存的彩色图像的rgb文件夹和储存深度图像的depth文件夹以及几个引导的txt文件。这时我们开始构建我们需要引导txt文件。
运行代码：
python associate.py rgb.txt depth.txt > associate.txt
（将彩色图和深度图按照时间匹配，并把顺序信息保存在associate.txt中）
python associate.py associate.txt groundtruth.txt > associate_with_groundtruth.txt
（将图像信息与真值进行匹配，并将其顺序信息保存在associate_with_groundtruth.txt内）
最后数据集处理为下图所示：
2.EPnP算法及BA优化的实践
PnP，全称Perspective-n-Points，是一种求解3D到2D点对的方法，描述的是当知道n个3D空间点的位置及其投影时，如何估计出相机的位姿。其中，EPnP，亦称为Efficient PnP方法比较普适，而且在书中也有提及。相信大部分读者都已经将《视觉slam十四讲》这本书已经看了，所以这次实验对比也就将基本参照书中的顺序进行。
EPnP算法大致情况和P3P类似，具体算法介绍可以参考博客：https://blog.csdn.net/jessecw79/article/details/82945918。大体上，EPnP并不属于一种迭代算法，它与OpenCV里面所提供的solvePnP()函数中所使用的默认迭代算法在实际使用过程中差异较大。实际上在本次数据集中PnP函数里，可以修改solvePnP函数的最后一个参数CV_EPnP为默认值，之后你会发现求解结果随着帧数的运行是震荡的。虽然OpenCV已经将这个算法封装好但是我们还是稍微了解一下EPnP的算法流程。EPnP的核心思想是将世界坐标系中所测得的3D坐标表示为一组虚拟的控制点的加权和，一般虚拟控制点是不能共面的4个为了能够求得精确解。首先，我们要处理所测得的3D参考点，让其转化成具有代表性的4个控制点；其次，计算由控制点加权得到的n个3D参考点的坐标；再则，计算3D参考点在世界坐标系下和相机坐标系下的的的重心及偏心矩阵；最后，利用偏心矩阵之家所具有的旋转和位移不变的性质求出相机的位姿。
BA优化，Bundle Adjustment，实际上就是最小化重投影误差问题。书中用的是图优化方法（当然还有谷歌开发的ceres库可以调用），而且讲的也比较细，所以本次实验也将使用图优化方法。刚开始看书的时候感觉图优化用的这个库g2o（General Graph Optimization "通用图优化"）基本看完一遍没啥感觉，毕竟图优化这个图论基础跟我们从小学到大的数论差的还是挺远的。g2o相当于是利用了图（graph）的方式描述了一个最小二乘问题，详细的g2o求解过程可以参考博客：https://blog.csdn.net/qit1314/article/details/84886612。这里大致上提一下：首先根据重投影得到误差，然后根据误差方程得到关于相机位姿的雅克比矩阵，目前这些书上都有推导。然后是g2o中所特有的构建迭代方程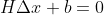
进行迭代求解，这里的H和b的构造和之前所求得的误差向量及雅克比矩阵有关。
现在开始实际数据集测试。（代码会在博客最后给出）
首先是对数据集freiburg1_desk的前20帧进行EPnP相机位姿求解。这里参考帧为第一帧，用ORB算法采集第一帧的特征点及特征点所对应的深度值。然后同样，用ORB算法采集后19帧的特征点，并将其与第一帧参考帧的特征点进行汉明距离的特征匹配（这些都是最简单的，实际中不可能这样搞）。最后用OpenCV中封装好的solvePnP进行求解。由此构建EPnP问题的求解模型。
为了对EPnP算法性能有更直观感受，也为了增强一点SLAM算法的实际工程经验，在此，博客将引入数据集的真值与所计算出来的测量值进行比较，并记录产生的误差。对于相机位姿误差，为了能够直观比较，将误差分为旋转误差和平移误差进行比较。同时，由于其真值所包含了实际世界坐标系关于x,y,z方向的定义以及其绝对坐标值，所以实验将会以第一帧的绝对位姿为参考，将所求得的相应R及t之类的相机位姿变换作为改帧的相对变换叠加在第一帧的绝对位姿上，并将其结果与正在测量的改帧的真实值进行比较误差。旋转误差将会折算到我们常用的roll，pitch，yaw欧拉角上进行分别比较，平移误差将会折算到x，y，z三轴上进行分别比较，这样能比较直观地说明问题。实际上，在SLAM系统，初值永远不可能精准，目前这种做法只是为了体验一下算法的优化。
对于EPnP算法而言，其前20帧的误差变化如下所示：
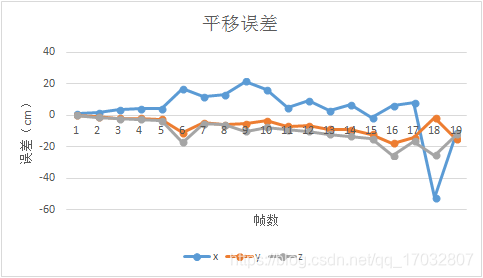
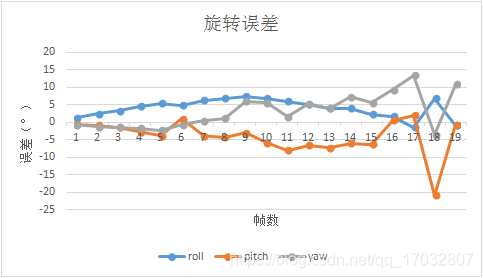
可以和明显地看到随着帧数的增加，不论是平移误差还是旋转误差都在震荡加剧。造成这种现象的本质原因还是因为随着帧数的增加，相机与初始位置的baseline相差加大，关键点估计精度会上升但是精确度会下降。可以从groundtruth.txt文件中看到，最后第20帧的相机位置和第1帧的位置相比，在x轴上移动了4.8cm，在y轴上移动了24.93cm，在z轴上移动了6.17cm。但是如果就这个原因而言，实验最后所得到的结果还是比实际位移相差较远，甚至称不上是误差。
一般造成这种现象的直接原因有两种：一是参考帧选择不合适，可能是参考帧rgb图比较模糊，或是深度图存在较大不准确性，导致所测得的特征点并不能代表实际图像的特征，以至于EPnP的求解一开始便出现了问题。根据平移误差图，在第7帧（第6次运动）有一个较大的突变，误差值突然上升。再看一下ORB特征点算法所得到的匹配点，第6帧算法执行情况如下所示。
很明显，ORB算法出现了误匹配，就比如那两个呈三角形堆放盒子上的特征点所引出的绿线。而反观之前的5帧，其特征点匹配线还是相当平齐的，大家可以后续试一下，有一个直观的感受。
第二个原因对于后续误差震荡，不难发现特征点减少加剧，而且误匹配情况更加严重。在第1帧和第2帧特征点匹配时，有177对特征点匹配上了，但是到了第19帧，也就是变换了18次的时候，特征点减少到只有91对匹配上的情况，减少了48%，这个还是比较明显的，可以看一下第1帧和第18帧的截图。
这匹配结果明显还不如第6帧。当然明显可以看到，相机已经有了一个旋转，这是误差更大的原因。
**结论：**EPnP结果非常依赖于特征点的选取及匹配。ORB特征点识别方法理论上是没有什么太大问题的，毕竟目前使用最广的特征点方法的SLAM------ORB_SLAM2方法所采取的特征点识别方法就是ORB识别，但是它用的ORB识别跟OpenCV中使用的ORB识别方法不一样。我们可以看到这个实验所识别到特征点基本集中在一些纹理比较复杂的区域（书和路由器），ORB_SLAM2所使用的是将ORB特征点均匀分布在图像上，并不会产生这样的集中现象。
那么问题来了，特征点密集有什么坏处呢？首先，假如图像纹理信息不丰富，比如高速路上，这样很容易让特征点法识别不到主要物体的图像特征而是在估计一些次要的特征甚至是噪声。其次，EPnP是需要3D深度数据的，由于Kinect之类的深度传感器本来这个数据可靠度就很一般，假如特征点所在的那一块深度信息并不可靠，那出现误差就很正常了，甚至于，出现假如点的深度信息完全不对，那样姿态估计就飘了。
其次，对于参考帧的问题。一般大型SLAM系统中往往会引入关键帧的概念。什么是关键帧呢，就是一个有代表性的帧，能够代表接下来几帧以至于下一个关键帧的相机对环境的感知。关键帧说白了就是相机在这个算法过程中连续运动状态的一个代表，一来可以简化计算量，二来可以作为参考帧来估计新加入的帧。我们这次实验仅仅就是拿了第1帧当作关键帧对后续进行估计，从实验结果来看第1帧显然并不能当作关键帧来用，至少是5帧后的。所以说，关键帧的选取也是至关重要的。
接下来看利用g2o库进行BA优化。在这个BA优化过程中，图的节点是相机位姿已经3D路标点，边是3D点在各个帧上的2D投影与实际测量的2D坐标的误差，这样进行优化。在执行优化时，我们将用EPnP求得的相机位姿矩阵的值作为初值进行g2o优化。
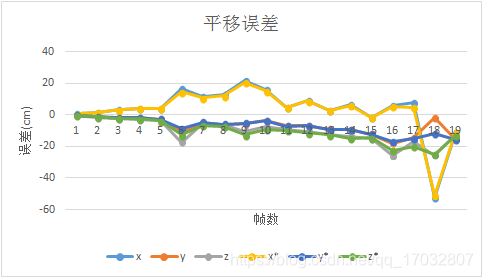
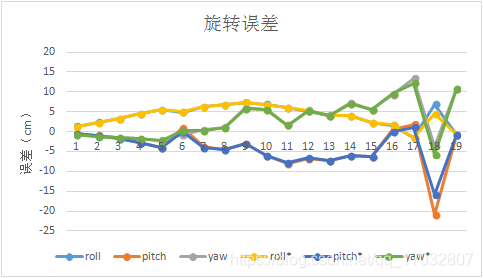
其中带有*的曲线为优化后曲线。根据上述图，优化前后并没有误差虽然说收敛了，但是并没有产生太大的变化，可能是已经陷入当前状态下的局部最优环境中了。为了防止出现EPnP所计算出的偏差过大的初值影响g2o算法的迭代计算，接下了又将相机初值设置为万能的零初始状态再进行一遍计算，顺便看一下g2o的优化能力，其误差曲线如下图所示。
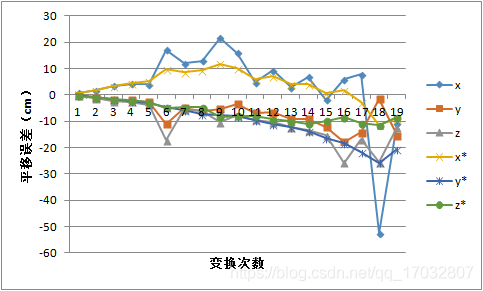
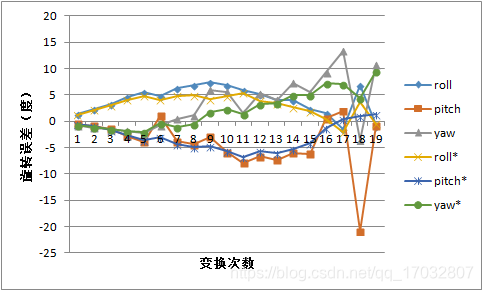
从实验结果曲线来看，g2o优化很大程度上改变了EPnP初值所带来的局部最优的影响。相较于EPnP而言，g2o优化更为平滑，而且不论平移误差还是旋转误差，其值都相对而言减少了很多。实际上EPnP也是利用迭代进行数值求解。为了验证初值对g2o优化的影响，我们将初值为EPnP所得解得优化结果（1）和初值为零值（旋转矩阵为单位矩阵、平移矩阵为零向量矩阵）的优化结果进行了比较，其实验结果如下所示。
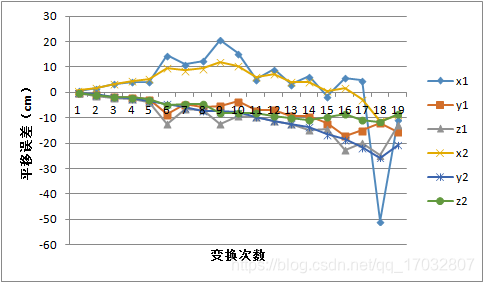
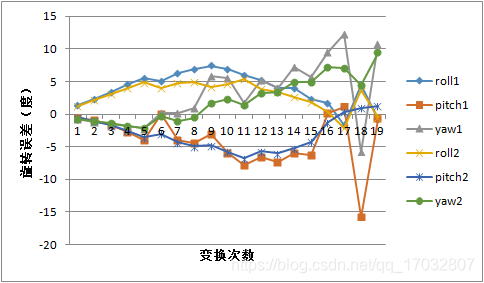
这优越性我觉得还是比较明显的。
**总结：**在PnP问题求解上，g2o所求的解得精度在是要高于OpenCV默认的EPnP的精度的；其次，由于求解的超平面具有非凸性，利用EPnP所求的解作为初值再用g2o进行优化很容易陷入局部最优；再则，关键帧，或者说是参考帧的选取比较重要，长基线情况下大部分算法都不会太稳定，其值并不会太可靠。
那么是否真的是因为基线过大而导致的数据振荡呢？在之前的实验中，确实误差是逐渐增长并振动的，第二帧的误差明显比其他帧要小的多。假如，我们的参考帧也就是关键帧并不是一直设定为第一帧，而是设定为前一帧的话，是否后续误差能够保持小基线的优势呢？我修改了一下程序又做了个实验。在新的实验中，我们将上一帧设置为参考帧，新的一帧设置为当前帧，并对这两帧进行相机姿态或者说是位姿变换的估计。总共测量两种误差，第一种种误差是逐次误差，用于验证小基线是否能够提高单次测量精度，第二种误差是累计误差，用于观测小基线操作是否能够提高总体测量精度。实验结果如下，首先是逐次测量的结果。
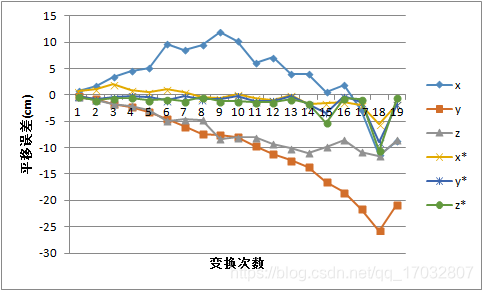
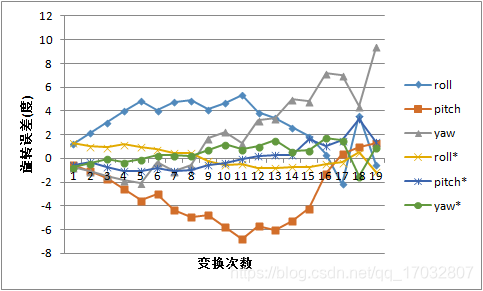
没有*号的是之前能得到比较好结果g2o算法优化后的误差数据，加了*号的是逐次误差数据。这次实验显然很好地证明了确实小基线能够得到比较稳定的精确解。但是这个对比实验是不均等假设的。对于g2o的优化，我们是假设第一帧为参考帧，后续帧都是在以第一帧真值的情况下，施加我们计算所得来的旋转和平移，在和实际这一帧的真值做比较。但是逐次比较的方法是以上一帧为参考帧的真值为基础，施加旋转和平移在和这一帧的真值比较来得出误差。这显然在实际工程中是不可能实现的，这基本就要求我们得知道所有，或者说是绝大部份帧的真值。
那么，就有人说了，退一步的讲，既然我们小基线能够保证这么小的误差，那就把上一帧的情况叠加进来嘛，反正最后误差也不会太大。没错，我也在逐次误差代码上修改了几段代码做了个累计误差的测试。
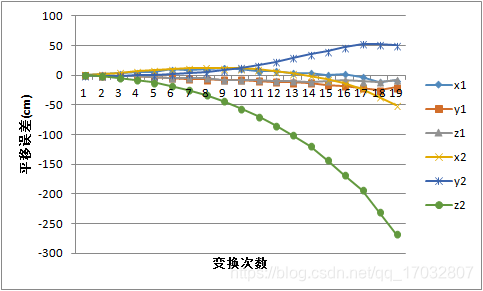
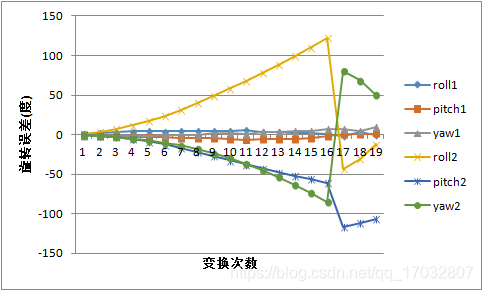
1代表着g2o的优化结果，2代表着累计误差。这两幅图很明显地向我们展示了什么叫做"漂移"。不论平移误差还是旋转误差（旋转误差超过180我们认定为换向），不论x、y、z还是roll、pitch、yaw，都很稳定地发散了出去。反观g2o的误差，反而显得比较小。这说明，小基线并不意味着高精度。这也验证了：大部分情况下，小基线SLAM有高稳定性，但是缺乏准确性；大基线SLAM有时有着良好的准确性，但是缺乏稳定。
所以由此可见，回环检测以及特征点提取对于基于特征点的SLAM算法是多么地重要（或者用位姿图来优化）。可以看一下我之前写的博客里有关于基于ORB均匀提取的算法，按道理来讲，特征点均匀分布在图像中会让姿态求解的结果好很多。这里并不是一个重点，所以在此点到为止留个大家自己去设计改良。本博客主要是为了完成书上的算法比较，所以接下来将会开始习题7-6的算法比较。
3.g2o优化中加入第一个相机位姿的观测
在g2o优化中，我们将当前帧的相机位姿和参考帧的3d点作为图优化的顶点vertex，3D点投影到当前帧的期望值与当前的观测值所得到的误差作为图优化的边edge，当然还有相机参数，这样进行优化得到优化后的相机位姿。在习题7-6以及文中都提到过，可以将第一帧的位姿和观测都添加到图优化中。那么，图优化的定点就包括第一个相机的位姿和第二个相机的位姿，3D点（路标）的坐标两块，这两块刚好是优化变量的部分，也就是书上推导的那两个雅克比矩阵。3D点在两个帧上的投影与实际观测值所构成的误差便是图优化的边。
理论上来讲，这种做法会使定点数量增加一个但是边的数量增加一倍，计算量增加往往会伴随结果精确度的提升，但是事实是否真的是这样呢，大家可以进一步用实验验证一下。