文章目录
当你迷茫的时候,请回头看看 目录大纲,也许有你意想不到的收获
前言
前面讲到几篇,都是 线性回归问题 的求解,目标是找到一条 直线来拟合,求解方式有 最小二乘法,正规方程,梯度下降法。
现在讲讲另一种回归问题,就是 逻辑回归,也就是分类问题,分类问题也包括二分类 与 多分类 问题。
-
二分类:输出是(1)或否(0),例如逻辑门,与门、或门、非门、异或门等等。 -
多分类:输出的是多个值,对应着每个分类的概率,是小于或等于 1 的值。最经典的例子莫过于手写数字的识别,给出一张手写的数字图片,最后输出是各个数字(1~9)的概率,比如我手写了一个 7,像 7 又像 1,那么多分类输出可能为:7 有 0.9 概率,1 有 0.1 的概率,其他数字概率接近于 0。
二分类问题
先简单点,讨论二分类问题,例如 异或门:

真值表为:
| 样本 i 样本 i 样本i | x i 1 x_{i1} xi1 | x i 2 x_{i2} xi2 | y i y_i yi |
|---|---|---|---|
| i=1 | 0 | 0 | 0 |
| i=2 | 0 | 1 | 1 |
| i=3 | 1 | 0 | 1 |
| i=4 | 1 | 1 | 0 |
可以把真值表中的每一行都看作是一个样本, x i 1 x_{i1} xi1 与 x i 2 x_{i2} xi2 为异或门的 第 i 个样本输入, y i y_i yi 为第 i 个样本的输出。
多元线性函数
u = w 1 x 1 + w 2 x 2 + . . . + b u=w_1x_1+w_2x_2+...+b u=w1x1+w2x2+...+b
σ \sigma σ 函数
σ ( x ) = 1 1 + e − x = e x 1 + e x \sigma(x)=\frac{1}{1+e^{-x}}=\frac{e^x}{1+e^x}\\[10pt] σ(x)=1+e−x1=1+exex
可以看出: σ ( x ) ∈ ( 0 , 1 ) \sigma(x) \in (0,1) σ(x)∈(0,1),如果令 P = σ ( x ) P=\sigma(x) P=σ(x),那么有 x = ln P 1 − P x=\ln{\frac{P}{1-P}} x=ln1−PP,这个也比较好推导:
∵ σ ( x ) = 1 1 + e − x = P ∴ 1 + e − x = 1 P ∴ e − x = 1 P − 1 = 1 − P P ∴ x = − ln 1 − P P = ln P 1 − P \because\sigma(x)=\frac{1}{1+e^{-x}}=P\\[10pt] \therefore 1+e^{-x}=\frac{1}{P}\\[10pt] \therefore e^{-x}=\frac{1}{P}-1=\frac{1-P}{P}\\[10pt] \therefore x=-\ln{\frac{1-P}{P}}=\ln{\frac{P}{1-P}} ∵σ(x)=1+e−x1=P∴1+e−x=P1∴e−x=P1−1=P1−P∴x=−lnP1−P=ln1−PP
σ ( x ) \sigma(x) σ(x) 导数:
σ ′ ( x ) = − 1 ( 1 + e − x ) 2 ⋅ ( 1 + e − x ) ′ = e − x ( 1 + e − x ) 2 = 1 1 + e − x ⋅ e − x 1 + e − x = 1 1 + e − x ⋅ ( 1 − 1 1 + e − x ) ∴ σ ′ ( x ) = σ ( x ) ⋅ ( 1 − σ ( x ) ) \sigma'(x)=-\frac{1}{(1+e^{-x})^2} \cdot (1+e^{-x})'=\frac{e^{-x}}{(1+e^{-x})^2}\\[10pt] =\frac{1}{1+e^{-x}} \cdot \frac{e^{-x}}{1+e^{-x}} =\frac{1}{1+e^{-x}} \cdot (1- \frac{1}{1+e^{-x}})\\[10pt] \therefore \sigma'(x)= \sigma(x)\cdot (1-\sigma(x))\\[10pt] σ′(x)=−(1+e−x)21⋅(1+e−x)′=(1+e−x)2e−x=1+e−x1⋅1+e−xe−x=1+e−x1⋅(1−1+e−x1)∴σ′(x)=σ(x)⋅(1−σ(x))
输出函数
将线性函数与 σ \sigma σ 函数结合在一起,得到一个函数 σ ( u ) \sigma(u) σ(u),这里把 b 也看作是 w n w_n wn,相应地 x n x_n xn 也就为 1
σ ( u ) = 1 1 + e − u = 1 1 + e − ( w 1 x 1 + w 2 x 2 + . . . + w n x n ) \sigma(u)=\frac{1}{1+e^{-u}}=\frac{1}{1+e^{-(w_1x_1+w_2x_2+...+w_nx_n)}} σ(u)=1+e−u1=1+e−(w1x1+w2x2+...+wnxn)1
这里我令输出函数 z = σ ( u ) z=\sigma(u) z=σ(u),即
z = σ ( u ) = 1 1 + e − u = 1 1 + e − ( w 1 x 1 + w 2 x 2 + . . . + w n x n ) z=\sigma(u)=\frac{1}{1+e^{-u}}=\frac{1}{1+e^{-(w_1x_1+w_2x_2+...+w_nx_n)}}\\[10pt] z=σ(u)=1+e−u1=1+e−(w1x1+w2x2+...+wnxn)1
根据 σ \sigma σ 函数导数性质有:
z ′ = σ ′ ( u ) = σ ( u ) ⋅ ( 1 − σ ( u ) ) = z ( 1 − z ) z'=\sigma'(u)=\sigma(u)\cdot (1-\sigma(u))=z(1-z)\\[10pt] z′=σ′(u)=σ(u)⋅(1−σ(u))=z(1−z)
上面我们提到过 σ ( u ) ∈ ( 0 , 1 ) \sigma(u) \in (0,1) σ(u)∈(0,1),令 P = σ ( u ) P=\sigma(u) P=σ(u),那么有 u = ln P 1 − P u=\ln{\frac{P}{1-P}} u=ln1−PP,P 可以看作是某个类别的概率,对于二分类来说,概率要么是 0,要么是 1,那么从概率的角度上看:
∵ P = σ ( u ) ∴ u = ln P 1 − P = ln P ( y = 1 ∣ x ) P ( y = 0 ∣ x ) \because P=\sigma(u)\\[10pt] \therefore u=\ln{\frac{P}{1-P}}=\ln{\frac{P(y=1|x)}{P(y=0|x)}} ∵P=σ(u)∴u=ln1−PP=lnP(y=0∣x)P(y=1∣x)
y 为真实标签,u 的含义为 事件为1的概率 P ( y = 1 ∣ x ) P(y=1|x) P(y=1∣x) 与 事件为0的概率 P ( y = 0 ∣ x ) P(y=0|x) P(y=0∣x) 比值再取对数。
似然函数
似然(likelihood),一听这个名字就知道是以前的老前辈翻译的,带有文言色彩
似然:相似的样子
假设总共有 m 个样本,第 i 个样本, 二分类 的似然函数如下,其中 z i z_i zi 为预测输出, y i y_i yi 为实际输出:
L ( w ) = ∏ i = 1 m z i y i ( 1 − z i ) ( 1 − y i ) % 似然函数 L(w)=\prod\limits_{i=1}^{m} z_i^{y_i}(1-z_i)^{(1-y_i)}\\[10pt] L(w)=i=1∏mziyi(1−zi)(1−yi)
要注意的是,这里 y i y_i yi 与 1 − y i 1-y_i 1−yi 其中有一个为 0, y i y_i yi 要么为 0,要么为 1(二分类),令:
w = [ w 1 w 2 ... w n ] , x i = [ x i 1 x i 2 ... x i n ] z i = σ ( w T x i ) % w 参数 w=\begin{bmatrix} w_1\\w_2\\\dots\\ w_n \end{bmatrix}, % x 输入 x_i=\begin{bmatrix} x_{i1}\\x_{i2}\\\dots\\ x_{in} \end{bmatrix}\\[10pt] z_i=\sigma(w^Tx_i)\\[10pt] w= w1w2...wn ,xi= xi1xi2...xin zi=σ(wTxi)
为了方便,可以对似然函数取对数,就由乘法转为了加法,称之为 对数似然函数:
ℓ ( w ) = ln L ( w ) = ln ( ∏ i = 1 m z i y i ( 1 − z i ) ( 1 − y i ) ) = ∑ i = 1 m [ y i ln z i + ( 1 − y i ) ln ( 1 − z i ) ] \ell(w)=\ln{L(w)}=\ln{(\prod\limits_{i=1}^{m} z_i^{y_i}(1-z_i)^{(1-y_i)})}\\[10pt] =\sum\limits_{i=1}^{m}[{y_i\ln{z_i}}+{(1-y_i)\ln{(1-z_i)}}] ℓ(w)=lnL(w)=ln(i=1∏mziyi(1−zi)(1−yi))=i=1∑m[yilnzi+(1−yi)ln(1−zi)]
因为输出 z i ∈ ( 0 , 1 ) z_i \in(0,1) zi∈(0,1),所以 ln z i \ln{z_i} lnzi 或者 ln ( 1 − z i ) \ln(1-z_i) ln(1−zi) 都是负数,因此 负对数似然 为正数:
L N L L ( w ) = − ∑ i = 1 m [ y i ln z i + ( 1 − y i ) ln ( 1 − z i ) ] \mathcal{L}{NLL}(w)= - \sum\limits{i=1}^{m}[{y_i\ln{z_i}}+{(1-y_i)\ln{(1-z_i)}}] LNLL(w)=−i=1∑m[yilnzi+(1−yi)ln(1−zi)]
极大似然估计
还记得我们前面的最小二乘法吗?目标是最小残差平方和(RSS),通过 RSS 来判断函数拟合的优劣,那么对于回归回题,目标则是求极大似然估计,似然函数或对数似然函数越大,等效于负对数似然越小,函数拟合的就越好。
求极大似然估计,等效于要求负对数似然极小。这就和最小化残差平方和有点相似了,都是求最小,就可以采用梯度下降法进行求解。
梯度下降法
函数准备
令 i 为样本号,eg. z i z_{i} zi 为第 i 个样本预测概率, y i y_{i} yi 为真实概率,有:
u i = w 1 x i 1 + w 2 x i 2 + . . . + b = [ x i 1 x i 2 ... 1 ] [ w 1 w 2 ... b ] z i = σ ( u i ) = 1 1 + e − u i u_{i}=w_{1}x_{i1}+w_{2}x_{i2}+...+b\\[10pt] =\begin{bmatrix} x_{i1}& x_{i2}&\dots& 1 \end{bmatrix} \begin{bmatrix} w_{1}\\ w_{2}\\\dots\\ b \end{bmatrix} \\[10pt] z_{i}=\sigma(u_{i})=\frac{1}{1+e^{-u_{i}}}\\[10pt] ui=w1xi1+w2xi2+...+b=[xi1xi2...1] w1w2...b zi=σ(ui)=1+e−ui1
可以把 b 作为 w n w_{n} wn,那么 x n = 1 x_{n}=1 xn=1 它们的偏导为:
∂ u i ∂ w k = x i k ∂ z i ∂ u i = z i ( 1 − z i ) \frac{\partial u_{i}}{\partial w_{k}} =x_{ik}\\[10pt] \frac{\partial z_{i}}{\partial u_{i}} =z_{i}(1-z_{i})\\[10pt] ∂wk∂ui=xik∂ui∂zi=zi(1−zi)
负对数似然函数为
L N L L ( w ) = − ∑ i = 1 m [ y i ln z i + ( 1 − y i ) ln ( 1 − z i ) ] \mathcal{L}{NLL}(w)= - \sum\limits{i=1}^{m}[{y_i\ln{z_i}}+{(1-y_i)\ln{(1-z_i)}}] LNLL(w)=−i=1∑m[yilnzi+(1−yi)ln(1−zi)]
令:
E i = − [ y i ln z i + ( 1 − y i ) ln ( 1 − z i ) ] ∴ L N L L ( w ) = ∑ i = 1 m E i E_{i}=-[{y_i\ln{z_i}}+{(1-y_i)\ln{(1-z_i)}}]\\[10pt] %% \therefore \mathcal{L}{NLL}(w)= \sum\limits{i=1}^{m}E_{i}\\[10pt] Ei=−[yilnzi+(1−yi)ln(1−zi)]∴LNLL(w)=i=1∑mEi
求偏导
∂ E i ∂ z i = − ( y i z i − 1 − y i 1 − z i ) = z i − y i z i ( 1 − z i ) %% \frac{\partial E_{i}}{\partial z_{i}} =-(\frac{y_{i}}{z_{i}}-\frac{1-y_{i}}{1-z_{i}})\\[10pt] =\frac{z_{i}-y_{i}}{z_{i}(1-z_{i})} \\[10pt] ∂zi∂Ei=−(ziyi−1−zi1−yi)=zi(1−zi)zi−yi
所以有:
∂ E i ∂ w k = ∂ E i ∂ z i ⋅ ∂ z i ∂ u i ⋅ ∂ u i ∂ w k = z i − y i z i ( 1 − z i ) ⋅ z i ( 1 − z i ) ⋅ x i k = ( z i − y i ) ⋅ x i k ∴ ∂ L N L L ∂ w k = ∑ i = 1 m ∂ E i ∂ w k = ∑ i = 1 m ( z i − y i ) ⋅ x i k \frac{\partial E_{i}}{\partial w_{k}} =\frac{\partial E_{i}}{\partial z_{i}} \cdot \frac{\partial z_{i}}{\partial u_{i}}\cdot \frac{\partial u_{i}}{\partial w_{k}}\\[10pt] =\frac{z_{i}-y_{i}}{z_{i}(1-z_{i})} \cdot z_{i}(1-z_{i}) \cdot x_{ik}\\[10pt] =(z_{i}-y_{i}) \cdot x_{ik}\\[10pt] %% \therefore\frac{\partial \mathcal{L}{NLL}}{\partial w{k}} =\sum\limits_{i=1}^{m}\frac{\partial E_{i}}{\partial w_{k}} =\sum\limits_{i=1}^{m}(z_{i}-y_{i}) \cdot x_{ik}\\[10pt] ∂wk∂Ei=∂zi∂Ei⋅∂ui∂zi⋅∂wk∂ui=zi(1−zi)zi−yi⋅zi(1−zi)⋅xik=(zi−yi)⋅xik∴∂wk∂LNLL=i=1∑m∂wk∂Ei=i=1∑m(zi−yi)⋅xik
损失函数
项目上多用均值作为损失函数,即:
E = 1 m L N L L ( w ) = 1 m ∑ i = 1 m E i = − 1 m ∑ i = 1 m [ y i ln z i + ( 1 − y i ) ln ( 1 − z i ) ] E=\frac{1}{m}\mathcal{L}{NLL}(w)=\frac{1}{m}\sum\limits{i=1}^{m}E_{i}\\[10pt] =-\frac{1}{m}\sum\limits_{i=1}^{m}[{y_i\ln{z_i}}+{(1-y_i)\ln{(1-z_i)}}]\\[10pt] E=m1LNLL(w)=m1i=1∑mEi=−m1i=1∑m[yilnzi+(1−yi)ln(1−zi)]
所以有:
∂ E ∂ w k = 1 m ∂ L N L L ∂ w k = 1 m ∑ i = 1 m ( z i − y i ) ⋅ x i k \frac{\partial E}{\partial w_{k}} =\frac{1}{m}\frac{\partial \mathcal{L}{NLL}}{\partial w{k}} =\frac{1}{m}\sum\limits_{i=1}^{m}(z_{i}-y_{i}) \cdot x_{ik}\\[10pt] ∂wk∂E=m1∂wk∂LNLL=m1i=1∑m(zi−yi)⋅xik
梯度更新
上面我们求出了偏导,是为了求梯度准备的。
再来翻译一下, 梯度:梯子的斜度,也就是斜率,对于多维度的梯度,就是每个维度方向上的斜率。
那么 E 的梯度为:
∂ E ∂ w ⃗ = [ ∂ E ∂ w 1 ∂ E ∂ w 2 ... ∂ E ∂ w n ] = [ 1 m ∑ i = 1 m ( z i − y i ) ⋅ x i 1 1 m ∑ i = 1 m ( z i − y i ) ⋅ x i 2 ... 1 m ∑ i = 1 m ( z i − y i ) ⋅ x i n ] \frac{\partial E}{\partial \vec{w}}=\begin{bmatrix} \frac{\partial E}{\partial w_{1}}\\[10pt] \frac{\partial E}{\partial w_{2}}\\[10pt] \dots\\[10pt] \frac{\partial E}{\partial w_{n}}\\[10pt] \end{bmatrix} =\begin{bmatrix} \frac{1}{m}\sum\limits_{i=1}^{m}(z_{i}-y_{i}) \cdot x_{i1}\\[10pt] \frac{1}{m}\sum\limits_{i=1}^{m}(z_{i}-y_{i}) \cdot x_{i2}\\[10pt] \dots\\[10pt] \frac{1}{m}\sum\limits_{i=1}^{m}(z_{i}-y_{i}) \cdot x_{in}\\[10pt] \end{bmatrix} ∂w ∂E= ∂w1∂E∂w2∂E...∂wn∂E = m1i=1∑m(zi−yi)⋅xi1m1i=1∑m(zi−yi)⋅xi2...m1i=1∑m(zi−yi)⋅xin
前面我们推导出沿着 梯度 方向下降最快:
Δ w k = η Δ r ∂ E ∂ w k w k ( t + 1 ) = w k ( t ) − η Δ r ∂ E ∂ w k \Delta{w_k}= \eta\Delta{r}\frac{\partial E}{\partial w_{k}} \\[10pt] w_{k}^{(t+1)}=w_{k}^{(t)} - \eta\Delta{r}\frac{\partial E}{\partial w_{k}} \\[10pt] Δwk=ηΔr∂wk∂Ewk(t+1)=wk(t)−ηΔr∂wk∂E
这里 Δ r \Delta{r} Δr 为 w 在梯度 l ⃗ \vec{l} l 方向增长一个微小单位,分解到各维度方向增长就是 Δ r cos θ k \Delta{r}\cos{\theta_k} Δrcosθk, θ k \theta_k θk 为梯度 l ⃗ \vec{l} l 与 w k w_k wk 维度方向的夹角。
η = 1 ∑ k = 1 n ( ∂ E ∂ w k ) 2 cos θ k = η ∂ E ∂ w k = ∂ E ∂ w k ∑ k = 1 n ( ∂ E ∂ w k ) 2 \eta=\frac{1}{\sqrt{\sum\limits_{k=1}^{n}{(\frac{\partial E}{\partial {w_k}})^2}}}\\[10pt] %% \cos{\theta_k}=\eta\frac{\partial E}{\partial {w_k}}=\frac{\frac{\partial E}{\partial {w_k}}}{\sqrt{\sum\limits_{k=1}^{n}{(\frac{\partial E}{\partial {w_k}})^2}}}\\[10pt] η=k=1∑n(∂wk∂E)2 1cosθk=η∂wk∂E=k=1∑n(∂wk∂E)2 ∂wk∂E
python 实战
以异或门为例:

真值表为:
| i i i | x i 1 x_{i1} xi1 | x i 2 x_{i2} xi2 | y i y_i yi |
|---|---|---|---|
| i=1 | 0 | 0 | 0 |
| i=2 | 0 | 1 | 1 |
| i=3 | 1 | 0 | 1 |
| i=4 | 1 | 1 | 0 |
可以把真值表中的每一行都看作是一个样本, x i 1 x_{i1} xi1 与 x i 2 x_{i2} xi2 为异或门的 第 i 个样本输入, y i y_i yi 为第 i 个样本的输出。
LogisticRegression
定义好逻辑回归训练类 LogisticRegression,包括前向计算,反向传播
python
import numpy as np
import matplotlib.pyplot as plt
from matplotlib.colors import ListedColormap
class LogisticRegression:
"""手动实现的逻辑回归"""
def __init__(self, learning_rate=0.1, n_iterations=10000):
self.lr = learning_rate
self.n_iter = n_iterations
self.weights = None
self.bias = None
self.losses = []
def sigmoid(self, z):
"""Sigmoid激活函数"""
return 1 / (1 + np.exp(-z))
def fit(self, X, y):
"""训练逻辑回归模型"""
n_samples, n_features = X.shape
# 初始化参数
self.weights = np.random.randn(n_features)
self.bias = 0
# 梯度下降
for iteration in range(self.n_iter):
# 前向传播
u = np.dot(X, self.weights) + self.bias
z = self.sigmoid(u)
# 计算损失,避免log中出现0的情况,加上一个非常小的值
loss = -np.mean(y * np.log(z + 1e-15) +
(1 - y) * np.log(1 - z + 1e-15))
self.losses.append(loss)
# 计算梯度
dw = (1 / n_samples) * np.dot(X.T, (z - y))
db = (1 / n_samples) * np.sum(z - y)
# 更新参数
self.weights -= self.lr * dw
self.bias -= self.lr * db
# 打印进度
if iteration % 1000 == 0:
accuracy = self.score(X, y)
print(
f"Iteration {iteration}, Loss: {loss:.4f}, Accuracy: {accuracy:.4f}"
)
def predict_proba(self, X):
"""预测概率"""
linear_output = np.dot(X, self.weights) + self.bias
return self.sigmoid(linear_output)
def predict(self, X, threshold=0.5):
"""预测类别"""
probabilities = self.predict_proba(X)
return (probabilities >= threshold).astype(int)
def score(self, X, y):
"""计算准确率"""
predictions = self.predict(X)
return np.mean(predictions == y)训练及结果
准备样本数据进行训练并绘制损失函数,分别尝试 线性特征 与使用 多项式特征 来训练求解
python
def create_xor_data():
"""创建异或门数据"""
X = np.array([[0, 0], [0, 1], [1, 0], [1, 1]])
y = np.array([0, 1, 1, 0])
return X, y
def add_polynomial_features(X):
"""添加多项式特征解决线性不可分问题"""
# 添加平方项和交叉项
X_poly = np.hstack([
X,
X[:, 0:1]**2, # x1²
X[:, 1:2]**2, # x2²
(X[:, 0:1] * X[:, 1:2]), # x1*x2
])
return X_poly
def visualize_results(X, y, model, title, feature_type='linear'):
"""可视化决策边界和结果"""
fig, axes = plt.subplots(1, 2, figsize=(12, 5))
# 创建网格点
x_min, x_max = X[:, 0].min() - 0.5, X[:, 0].max() + 0.5
y_min, y_max = X[:, 1].min() - 0.5, X[:, 1].max() + 0.5
xx, yy = np.meshgrid(np.arange(x_min, x_max, 0.01),
np.arange(y_min, y_max, 0.01))
if feature_type == 'poly':
# 为多项式特征准备网格数据
grid = np.c_[xx.ravel(), yy.ravel()]
grid_poly = add_polynomial_features(grid)
Z = model.predict(grid_poly)
else:
grid = np.c_[xx.ravel(), yy.ravel()]
Z = model.predict(grid)
Z = Z.reshape(xx.shape)
# 绘制决策边界
axes[0].contourf(xx, yy, Z, alpha=0.4, cmap=ListedColormap(['#FFAAAA', '#AAAAFF']))
axes[0].scatter(X[:, 0], X[:, 1], c=y, s=100, cmap=ListedColormap(['red', 'blue']), edgecolors='k')
axes[0].set_xlabel('x1')
axes[0].set_ylabel('x2')
axes[0].set_title(f'Decision Boundary - {title}')
axes[0].grid(True, alpha=0.3)
# 绘制损失曲线
axes[1].plot(model.losses)
axes[1].set_xlabel('Iteration')
axes[1].set_ylabel('Loss')
axes[1].set_title('Loss Curve')
axes[1].grid(True, alpha=0.3)
plt.tight_layout()
plt.show()
def main():
# 1. 准备数据
X, y = create_xor_data()
print("原始数据:")
print("X:", X)
print("y:", y)
print()
# 2. 尝试线性特征(无法解决异或问题)
print("=" * 50)
print("1. 使用线性特征(应该失败):")
print("=" * 50)
model_linear = LogisticRegression(learning_rate=0.1, n_iterations=10000)
model_linear.fit(X, y)
print(f"线性模型准确率: {model_linear.score(X, y):.4f}")
print(f"权重: {model_linear.weights}, 偏置: {model_linear.bias:.4f}")
print(f"预测结果: {model_linear.predict(X)}")
visualize_results(X, y, model_linear, "Linear Features", 'linear')
# 3. 使用多项式特征(可以解决异或问题)
print("\n" + "=" * 50)
print("2. 使用多项式特征(应该成功):")
print("=" * 50)
X_poly = add_polynomial_features(X)
print("多项式特征形状:", X_poly.shape)
print("特征示例:", X_poly[0])
model_poly = LogisticRegression(learning_rate=0.1, n_iterations=20000)
model_poly.fit(X_poly, y)
print(f"多项式模型准确率: {model_poly.score(X_poly, y):.4f}")
print(f"权重: {model_poly.weights}, 偏置: {model_poly.bias:.4f}")
print(f"预测结果: {model_poly.predict(X_poly)}")
# 显示详细预测
print("\n详细预测:")
for i in range(len(X)):
prob = model_poly.predict_proba(X_poly[i:i+1])[0]
pred = model_poly.predict(X_poly[i:i+1])[0]
print(f"X={X[i]}, y={y[i]}, 预测概率={prob:.6f}, 预测类别={pred}")
visualize_results(X, y, model_poly, "Polynomial Features", 'poly')运行结果
运行 main() 得到如下结果:
-
使用线性特征
log原始数据: X: [[0 0] [0 1] [1 0] [1 1]] y: [0 1 1 0] ================================================== 1. 使用线性特征(应该失败): ================================================== Iteration 0, Loss: 0.6989, Accuracy: 0.5000 Iteration 1000, Loss: 0.6931, Accuracy: 0.5000 Iteration 2000, Loss: 0.6931, Accuracy: 0.7500 Iteration 3000, Loss: 0.6931, Accuracy: 0.7500 Iteration 4000, Loss: 0.6931, Accuracy: 0.7500 Iteration 5000, Loss: 0.6931, Accuracy: 0.7500 Iteration 6000, Loss: 0.6931, Accuracy: 0.7500 Iteration 7000, Loss: 0.6931, Accuracy: 0.7500 Iteration 8000, Loss: 0.6931, Accuracy: 0.7500 Iteration 9000, Loss: 0.6931, Accuracy: 0.5000 线性模型准确率: 0.5000 权重: [-2.48590055e-16 -2.48352572e-16], 偏置: 0.0000 预测结果: [1 1 1 1]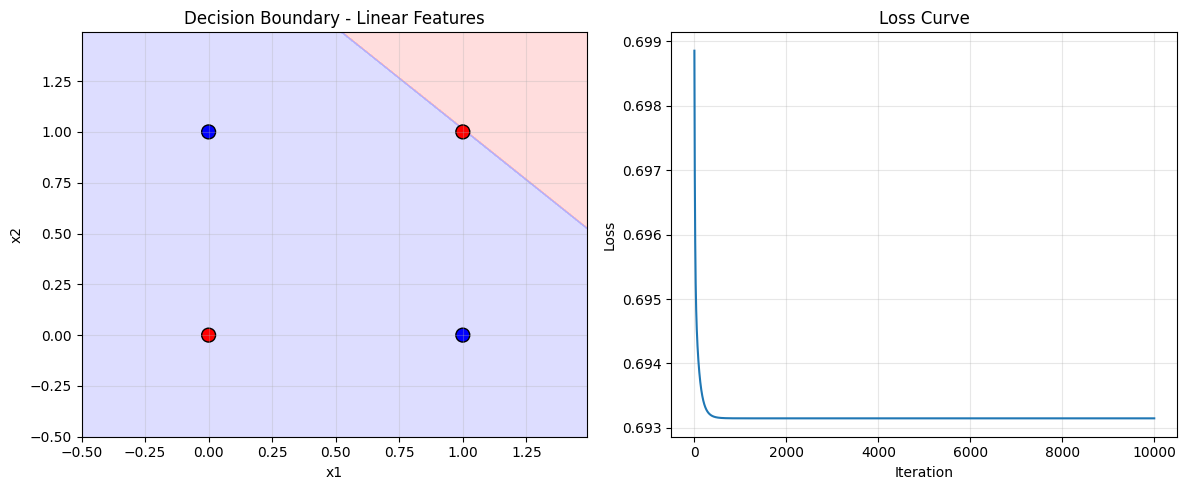
-
多项式特征
log================================================== 1. 使用多项式特征(应该成功): ================================================== 多项式特征形状: (4, 5) 特征示例: [0 0 0 0 0] Iteration 0, Loss: 0.9076, Accuracy: 0.5000 Iteration 1000, Loss: 0.2192, Accuracy: 1.0000 Iteration 2000, Loss: 0.1162, Accuracy: 1.0000 Iteration 3000, Loss: 0.0774, Accuracy: 1.0000 Iteration 4000, Loss: 0.0576, Accuracy: 1.0000 Iteration 5000, Loss: 0.0457, Accuracy: 1.0000 Iteration 6000, Loss: 0.0378, Accuracy: 1.0000 Iteration 7000, Loss: 0.0322, Accuracy: 1.0000 Iteration 8000, Loss: 0.0280, Accuracy: 1.0000 Iteration 9000, Loss: 0.0248, Accuracy: 1.0000 Iteration 10000, Loss: 0.0223, Accuracy: 1.0000 Iteration 11000, Loss: 0.0202, Accuracy: 1.0000 Iteration 12000, Loss: 0.0184, Accuracy: 1.0000 Iteration 13000, Loss: 0.0170, Accuracy: 1.0000 Iteration 14000, Loss: 0.0157, Accuracy: 1.0000 Iteration 15000, Loss: 0.0146, Accuracy: 1.0000 Iteration 16000, Loss: 0.0137, Accuracy: 1.0000 Iteration 17000, Loss: 0.0129, Accuracy: 1.0000 Iteration 18000, Loss: 0.0121, Accuracy: 1.0000 ... X=[0 0], y=0, 预测概率=0.014450, 预测类别=0 X=[0 1], y=1, 预测概率=0.989687, 预测类别=1 X=[1 0], y=1, 预测概率=0.989687, 预测类别=1 X=[1 1], y=0, 预测概率=0.008247, 预测类别=0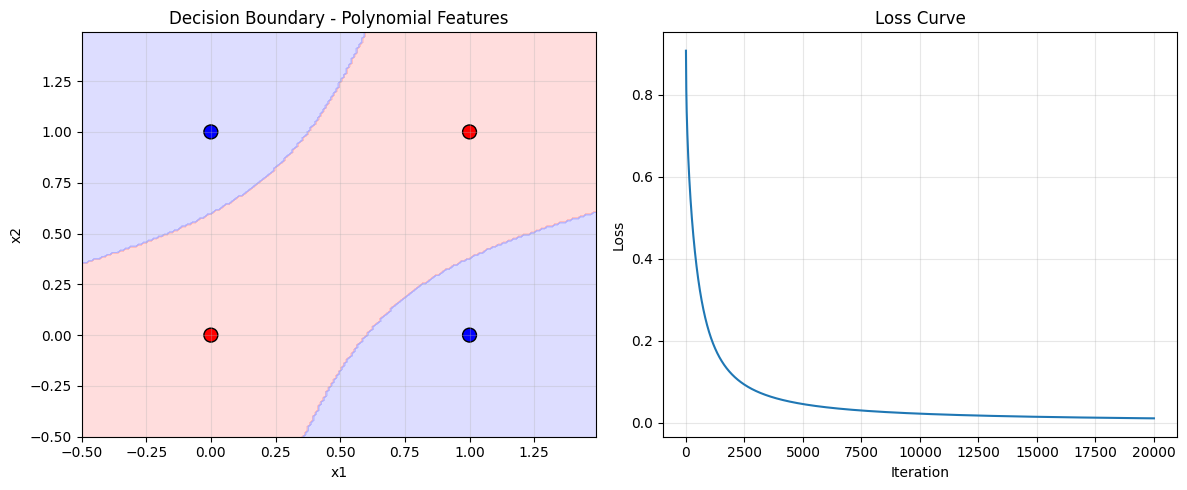
总结
-
逻辑回归是
线性分类器,决策边界是超平面:w 1 x 1 + w 2 x 2 + . . . + w n x n = 0 w_1x_1+w_2x_2+...+w_nx_n=0 w1x1+w2x2+...+wnxn=0
-
对于
原始异或问题:bash(0,0) → 类别0 (0,1) → 类别1 (1,0) → 类别1 (1,1) → 类别0在二维空间中,不存在一条直线能完美分离这 4 个点。这是线性不可分问题的经典例子。
-
解决方案:
特征映射通过添加多项式特征,将数据映射到高维空间:
x 1 x 2 \] → \[ x 1 x 2 x 1 2 x 2 2 x 1 x 2 \] \\begin{bmatrix} x_1 \& x_2 \\end{bmatrix} \\rightarrow \\begin{bmatrix} x_1 \& x_2 \& {x_1}\^2 \& {x_2}\^2 \& {x_1x_2} \\end{bmatrix} \[x1x2\]→\[x1x2x12x22x1x2
那么决策边界就变成了多项式
w 1 x 1 + w 2 x 2 + w 3 x 1 2 + w 4 x 2 2 + w 5 x 1 x 2 = 0 w_1x_1+w_2x_2+w_3{x_1}^2+w_4{x_2}^2+w_5{x_1x_2}=0 w1x1+w2x2+w3x12+w4x22+w5x1x2=0
在高维空间中,数据变得线性可分,这就是神经网络中 隐藏层 的思想基础。