【NIPS25 Best Paper】论文阅读

文章目录

• [Why Diffusion Models Don't Memorize: The Role of Implicit Dynamical Regularization in Training](#Why Diffusion Models Don’t Memorize: The Role of Implicit Dynamical Regularization in Training)
• • [1. 摘要](#1. 摘要)
  • [2. 问题背景与研究动机](#2. 问题背景与研究动机)
  • [3. 唯象学观察：训练动力学的实证分析](#3. 唯象学观察：训练动力学的实证分析)
  • • [3.1 时间尺度的分离](#3.1 时间尺度的分离)
    • [3.2 关键缩放律 (Scaling Laws)](#3.2 关键缩放律 (Scaling Laws))
    • [3.3 排除样本重复的影响](#3.3 排除样本重复的影响)
  • [4. 理论解析：高维随机特征模型 (RFNN)](#4. 理论解析：高维随机特征模型 (RFNN))
  • • [4.1 模型设定](#4.1 模型设定)
    • [4.2 谱分析 (Spectral Analysis)与时间尺度](#4.2 谱分析 (Spectral Analysis)与时间尺度)
  • [5. 相图与正则化机制 (Phase Diagram)](#5. 相图与正则化机制 (Phase Diagram))
  • [6. 对从业者的启示](#6. 对从业者的启示)
  • [7. 结论](#7. 结论)
• [Does Reinforcement Learning Really Incentivize Reasoning Capacity in LLMs Beyond the Base Model](#Does Reinforcement Learning Really Incentivize Reasoning Capacity in LLMs Beyond the Base Model)
• • [1. 摘要](#1. 摘要)
  • [2. 研究方法论](#2. 研究方法论)
  • • [2.1 核心评估指标：Pass@k](#2.1 核心评估指标：Pass@k)
    • [2.2 实验设置](#2.2 实验设置)
  • [3. 核心发现与实验结果](#3. 核心发现与实验结果)
  • • [3.1 现象：小 k 占优，大 k 劣势](#3.1 现象：小 k 占优，大 k 劣势)
    • [3.2 覆盖率分析 (Coverage Analysis)](#3.2 覆盖率分析 (Coverage Analysis))
    • [3.3 困惑度分析 (Perplexity Analysis)](#3.3 困惑度分析 (Perplexity Analysis))
    • [3.4 与蒸馏 (Distillation) 的对比](#3.4 与蒸馏 (Distillation) 的对比)
  • [4. 算法与训练动力学分析](#4. 算法与训练动力学分析)
  • • [4.1 采样效率差距 ( Δ S E \Delta_{SE} ΔSE)](#4.1 采样效率差距 ( Δ S E \Delta_{SE} ΔSE))
    • [4.2 训练过程中的退化](#4.2 训练过程中的退化)
  • [5. 结论与启示](#5. 结论与启示)
  • • [5.1 为什么 RLVR 没有带来新能力？](#5.1 为什么 RLVR 没有带来新能力？)
    • [5.2 未来方向](#5.2 未来方向)
• [Gated Attention for Large Language Models: Non-linearity, Sparsity, and Attention-Sink-Free](#Gated Attention for Large Language Models: Non-linearity, Sparsity, and Attention-Sink-Free)
• • [1. 摘要](#1. 摘要)
  • [2. 研究背景与动机](#2. 研究背景与动机)
  • [3. 方法论：门控注意力层 (Gated Attention Layer)](#3. 方法论：门控注意力层 (Gated Attention Layer))
  • • [3.1 探索的设计空间](#3.1 探索的设计空间)
    • [3.2 最佳实践结论](#3.2 最佳实践结论)
  • [4. 实验结果与性能分析](#4. 实验结果与性能分析)
  • • [4.1 模型性能提升](#4.1 模型性能提升)
    • [4.2 训练稳定性 (Training Stability)](#4.2 训练稳定性 (Training Stability))
  • [5. 机理分析：为什么门控有效？](#5. 机理分析：为什么门控有效？)
  • • [5.1 非线性增强低秩映射](#5.1 非线性增强低秩映射)
    • [5.2 引入输入依赖的稀疏性 (Input-Dependent Sparsity)](#5.2 引入输入依赖的稀疏性 (Input-Dependent Sparsity))
    • [5.3 消除 Attention Sink (Attention-Sink-Free)](#5.3 消除 Attention Sink (Attention-Sink-Free))
  • [6. 结论](#6. 结论)

Why Diffusion Models Don't Memorize: The Role of Implicit Dynamical Regularization in Training

xhs

1. 摘要

扩散模型（Diffusion Models, DMs）在生成任务中取得了巨大成功，但其避免记忆训练数据并实现泛化的机制尚不明确。本研究通过理论分析（高维随机特征模型）和数值实验（CelebA数据集上的U-Net）揭示了扩散模型训练过程中存在的一种 隐式动力学正则化（Implicit Dynamical Regularization） 机制。

核心发现包括：

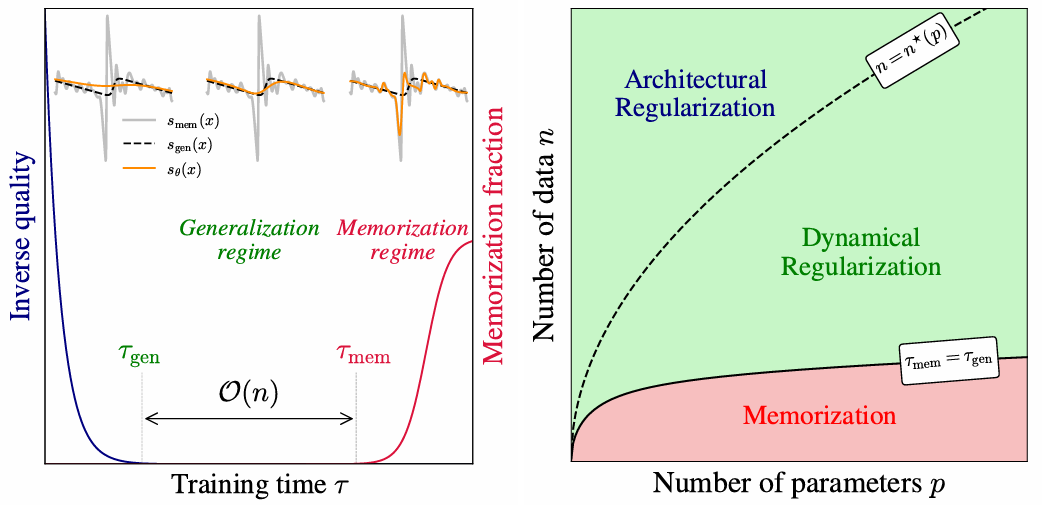
1. 双时间尺度分离 ：训练过程中存在两个显著分离的时间尺度。 τ g e n \tau_{gen} τgen 为模型生成高质量样本的起始时间， τ m e m \tau_{mem} τmem 为模型开始记忆训练数据的起始时间。
2. τ m e m \tau_{mem} τmem 的线性缩放律 ： τ m e m \tau_{mem} τmem 随训练集大小 n n n 线性增长（ τ m e m ∝ n \tau_{mem} \propto n τmem∝n），而 τ g e n \tau_{gen} τgen 保持恒定。这意味着随着数据量增加，有效泛化的时间窗口 [ τ g e n , τ m e m ] [\tau_{gen}, \tau_{mem}] [τgen,τmem] 会显著变宽。
3. 相变机制 ：研究识别了基于数据量 n n n 和模型参数量 p p p 的三个相变区域：记忆化区域、动力学正则化区域（泛化窗口）和架构正则化区域（ n > n ∗ ( p ) n > n^*(p) n>n∗(p)，过拟合完全消失） 。

---

2. 问题背景与研究动机

在当前的生成式建模中，扩散模型通过最小化分数匹配损失（score matching loss）来学习数据分布的分数函数 ∇ x log ⁡ P t ( x ) \nabla_x \log P_t(x) ∇xlogPt(x)。然而，理论上如果在经验分布上通过无限容量的模型进行训练，最优解（Empirical Score）应当是对应于训练样本的delta函数混合，这会导致模型在反向生成过程中完美复现训练样本（即记忆化）。

但在实践中，即使在过参数化（overparameterized）的设置下，扩散模型依然表现出优秀的泛化能力。本论文旨在解释这一现象，即训练动力学（Training Dynamics）和早停（Early Stopping） 如何在高维空间中阻止模型收敛到单纯记忆训练数据的解。

---

3. 唯象学观察：训练动力学的实证分析

作者在 CelebA 数据集上训练 U-Net 架构，通过改变训练集大小 n n n 和模型宽度 W W W（控制参数量 p p p），观察 FID（Fréchet Inception Distance）和记忆分数 f m e m f_{mem} fmem 的演变。

3.1 时间尺度的分离

• 泛化阶段 ( τ g e n \tau_{gen} τgen) ：训练初期，FID 迅速下降并在 τ g e n \tau_{gen} τgen 处达到最优。此时生成的样本具有高质量且未出现记忆化 ( f m e m ≈ 0 f_{mem} \approx 0 fmem≈0) 。
• 记忆化阶段 ( τ m e m \tau_{mem} τmem) ：随着训练继续，在 τ m e m \tau_{mem} τmem 时刻， f m e m f_{mem} fmem 开始上升，生成的样本逐渐逼近训练集中的最近邻样本。

3.2 关键缩放律 (Scaling Laws)

• 训练集大小 n n n 的影响 ：
  • τ g e n \tau_{gen} τgen 与 n n n 无关 。
  • τ m e m \tau_{mem} τmem 与 n n n 呈线性关系（ τ m e m ∝ n \tau_{mem} \propto n τmem∝n）。通过重缩放时间轴 τ / n \tau/n τ/n，不同 n n n 下的记忆化曲线完美重合。
  • 结论：增加数据量直接推迟了过拟合的发生，扩大了泛化窗口。
• 模型容量 p p p 的影响 ：
  • 随着模型宽度 W W W 增加， τ g e n ∝ W − 1 \tau_{gen} \propto W^{-1} τgen∝W−1 且 τ m e m ∝ n W − 1 \tau_{mem} \propto nW^{-1} τmem∝nW−1。
  • 更高容量的模型学得更快，也更早开始记忆，但只要 n n n 足够大，泛化窗口依然存在。

3.3 排除样本重复的影响

为了验证 τ m e m ∝ n \tau_{mem} \propto n τmem∝n 并非单纯因为样本被重复"观看"的次数，作者对比了固定 Batch Size 和 Full Batch（ B = n B=n B=n）的训练。结果显示，即使在 Full Batch 模式下（每一步更新所有样本都被使用）， τ m e m \tau_{mem} τmem 依然随 n n n 线性增长。这证明了记忆化是由损失景观（Loss Landscape）的性质决定的，而非样本重复频率 。

---

4. 理论解析：高维随机特征模型 (RFNN)

为了从数学上解释上述现象，作者利用高维极限下的随机特征神经网络（Random Features Neural Network, RFNN）进行了严格推导。

4.1 模型设定

• 分数函数近似 ： s A ( x ) = A p σ ( W x d ) s_A(x) = \frac{A}{\sqrt{p}}\sigma(\frac{Wx}{\sqrt{d}}) sA(x)=p Aσ(d Wx)，其中 W W W 是冻结的随机权重， A A A 是训练参数 。
• 高维极限 ：研究 n , p , d → ∞ n, p, d \to \infty n,p,d→∞ 的情况，保持比率 ψ n = n / d \psi_n = n/d ψn=n/d 和 ψ p = p / d \psi_p = p/d ψp=p/d 固定 。
• 动力学方程 ：在梯度流（Gradient Flow）下，参数 A ( τ ) A(\tau) A(τ) 的演化由核矩阵 U U U 的特征值决定 。

4.2 谱分析 (Spectral Analysis)与时间尺度

核心理论发现在于核矩阵 U U U 的特征值谱密度 ρ ( λ ) \rho(\lambda) ρ(λ) 在过参数化区域（ ψ p ≫ ψ n \psi_p \gg \psi_n ψp≫ψn）分裂为两个分离的"块（Bulk）" ：

1. 泛化块 ( ρ 2 \rho_{2} ρ2)：

   • 特征值量级： O ( ψ p ) \mathcal{O}(\psi_p) O(ψp)。
   • 物理意义：对应于总体协方差（Population Covariance），代表真实数据分布的结构（低频分量）。
   • 动力学影响：驱动训练的快速阶段，对应 τ g e n ∼ 1 / Δ t \tau_{gen} \sim 1/\Delta_t τgen∼1/Δt。在此阶段，模型学习总体分数（Population Score）， L t e s t ≈ L t r a i n \mathcal{L}{test} \approx \mathcal{L}{train} Ltest≈Ltrain 。

2. 记忆化块 ( ρ 1 \rho_{1} ρ1)：

   • 特征值量级： O ( ψ p / ψ n ) \mathcal{O}(\psi_p/\psi_n) O(ψp/ψn)。
   • 物理意义：对应于经验噪声（Empirical Noise），即训练样本特有的高频涨落。
   • 动力学影响：驱动训练的慢速阶段，对应 τ m e m ∝ ψ n \tau_{mem} \propto \psi_n τmem∝ψn。在此阶段，模型开始过拟合经验分数，导致记忆化 。

理论结论 ：由于特征值量级相差 ψ n \psi_n ψn 倍，导致对应的时间尺度 τ m e m \tau_{mem} τmem 与 τ g e n \tau_{gen} τgen 之间出现了 O ( n ) \mathcal{O}(n) O(n) 的分离。这为"隐式动力学正则化"提供了坚实的数学基础。

---

5. 相图与正则化机制 (Phase Diagram)

基于实验和理论，论文提出了 n − p n-p n−p 平面上的三个状态区域 ：

1. 记忆化区域 (Memorization Regime)：

   • 条件： n n n 较小， p p p 较大。
   • 现象： τ m e m ≈ τ g e n \tau_{mem} \approx \tau_{gen} τmem≈τgen，模型在学习到有效特征的同时迅速过拟合。

2. 动力学正则化区域 (Dynamical Regularization Regime)：

   • 条件： n n n 中等大小。
   • 现象： τ g e n ≪ τ m e m \tau_{gen} \ll \tau_{mem} τgen≪τmem。
   • 策略：存在显著的时间窗口，通过**早停（Early Stopping）**可以获得完美的泛化模型，避免记忆化。这是目前大多数大规模扩散模型工作的区域 。

3. 架构正则化区域 (Architectural Regularization Regime)：

   • 条件： n > n ∗ ( p ) n > n^*(p) n>n∗(p)。
   • 现象：即使 τ → ∞ \tau \to \infty τ→∞，模型也无法记忆数据。因为数据量超出了模型的表达能力（对于记忆噪声而言），模型被迫学习光滑的插值解。

---

6. 对从业者的启示

对于使用 Python/PyTorch 进行扩散模型开发的研究者，本论文提供了以下实践指导：

1. 早停至关重要 ：在数据量有限但模型庞大（过参数化）的场景下，记忆化几乎是必然的终点。必须监控生成质量（如 FID）并在 τ m e m \tau_{mem} τmem 之前停止训练。
2. 数据量的红利 ：增加训练数据 n n n 不仅是为了覆盖更多分布，更是为了线性地推迟 τ m e m \tau_{mem} τmem。如果计算资源允许，增加数据是扩大"安全训练窗口"的最有效手段 。
3. 优化器的选择 ：虽然论文主要分析 SGD，但实验证明 Adam 优化器 表现出相同的缩放规律（ τ m e m ∝ n \tau_{mem} \propto n τmem∝n），尽管 Adam 的收敛速度更快，导致绝对时间尺度缩短。在使用 Adam 时，需要更频繁地进行 Checkpoint 评估以捕捉泛化窗口。
4. 模型容量控制 ：增加模型宽度 W W W 会缩短 τ g e n \tau_{gen} τgen（学得更快），但也会线性缩短 τ m e m \tau_{mem} τmem。在小数据量下盲目增加模型大小可能导致泛化窗口过窄而难以控制。

---

7. 结论

本论文通过严谨的理论与实验论证了扩散模型之所以不记忆，并非因为它们不能，而是因为训练动力学中的 谱偏差（Spectral Bias） 优先学习低频的总体特征（泛化），而延迟了高频的样本特定噪声（记忆化）的学习。这种随数据量 n n n 线性增长的时间延迟，构成了扩散模型在过参数化设置下能够有效泛化的核心机制。

Does Reinforcement Learning Really Incentivize Reasoning Capacity in LLMs Beyond the Base Model

xhs
强化学习可以更有效的采样，但是基座模型决定性能上限
任意一个答案在模型中都有概率，只是不同模型中概率大小不同。rl能增大正确答案的概率不就是正确且有效的么。训练本来就不是创造答案，只是增加好的答案的概率。

1. 摘要

本研究对基于可验证奖励的强化学习（RLVR，如 OpenAI-o1 或 DeepSeek-R1 背后的技术）在提升大语言模型（LLM）推理能力方面的实际效果进行了批判性审查。尽管学界普遍认为 RLVR 能像传统 RL（如 AlphaGo）一样通过自我博弈发现新策略从而超越基座模型，但本文通过在大 k k k 值下的 pass@k 指标评测发现：

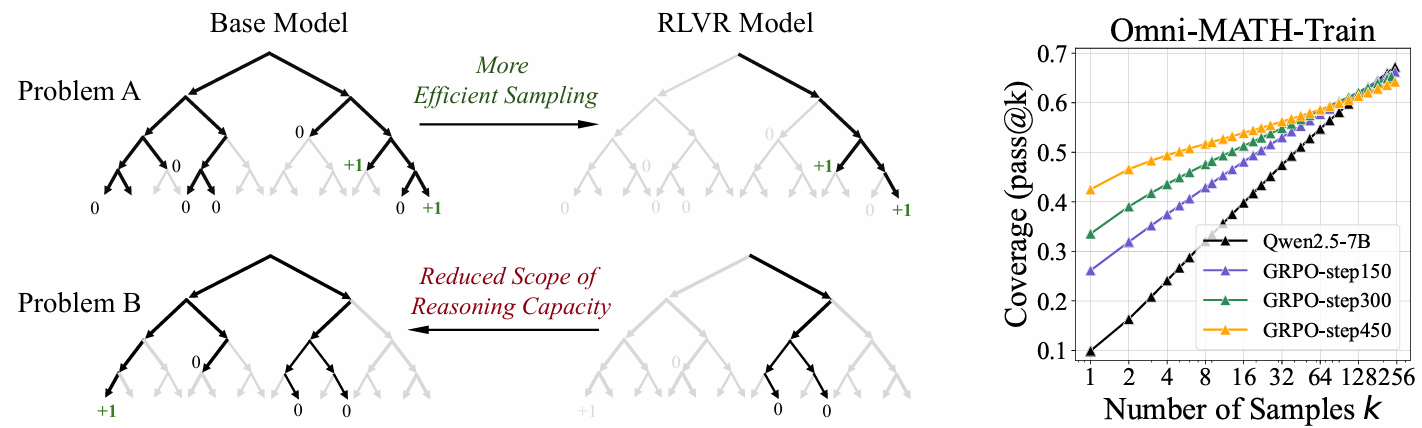
1. 推理边界收缩 ：RLVR 虽然提升了模型采样正确路径的概率（即提高了 pass@1），但实际上缩小了模型能解决问题的总范围。在 k k k 值较大（如 k = 256 k=256 k=256）时，基座模型（Base Model）的表现始终优于 RLVR 模型。
2. 缺乏新能力涌现：RLVR 模型生成的推理路径完全包含在基座模型的采样分布中，并未涌现出基座模型原本不具备的"新"推理模式。
3. 算法同质性 ：包括 PPO、GRPO、Reinforce++ 在内的六种主流 RLVR 算法表现相似，且距离充分挖掘基座模型潜力（即达到基座模型的 pass@k 上界）仍有巨大差距。
4. 与蒸馏的本质区别：与 RLVR 不同，知识蒸馏（Distillation）确实能够通过引入教师模型的模式来扩展模型的推理边界。

---

2. 研究方法论

2.1 核心评估指标：Pass@k

为了探究模型的"推理能力边界"（Reasoning Capacity Boundary），而非仅仅是平均表现，作者采用了 pass@k 指标。

• 定义 ：对于给定的问题，从模型中采样 k k k 个输出，若其中至少有一个通过验证，则视为解决。
• 物理意义 ：pass@k（特别是当 k k k 很大时）反映了模型潜在的能力上限。如果 RLVR 真的让模型学会了新的推理技能，那么在相同的 k k k 下，RLVR 模型理应解决一些基座模型无法解决的问题。
• 无偏估计器：为了降低方差，论文使用了以下无偏估计公式（Python 实现参考）：

2.2 实验设置

• 任务领域：数学（AIME, GSM8K, MATH, Minerva等）、代码生成（LiveCodeBench, HumanEval+）、视觉推理（MathVista）。
• 模型家族：Qwen2.5 (7B/14B/32B), LLaMA-3.1-8B, Qwen2.5-V。
• 对比对象：Base Model（无 Few-shot，避免 Prompt 干扰） vs. RLVR-Trained Model（如 SimpleRLZoo, Oat-Zero, DAPO 训练出的模型）。

---

3. 核心发现与实验结果

3.1 现象：小 k 占优，大 k 劣势

在所有测试基准中，作者观察到了一个一致的现象：

• k ≈ 1 k \approx 1 k≈1 时：RLVR 模型优于 Base 模型。这解释了为什么在常规 Leaderboard 上 RL 模型分数更高------它们极大提高了采样到正确答案的概率（Sampling Efficiency）。
• k k k 增大时 ：Base 模型的曲线更陡峭，迅速追上并反超 RLVR 模型。例如在 Minerva 基准测试中，32B Base 模型在 k = 128 k=128 k=128 时比 RL 模型高出约 9%。

3.2 覆盖率分析 (Coverage Analysis)

通过对比 Base 和 RLVR 模型能解决的问题集合，研究发现：

• RLVR 模型能解决的问题几乎是 Base 模型能解决问题的子集。
• 存在大量问题是 Base 模型能解决（在多次采样中）而 RLVR 模型完全无法解决的（即便 k k k 很大）。反之，RLVR 独有解决的问题极少。
• 结论：RLVR 并没有教会模型"新"的解题能力，而是让模型更倾向于输出其原有能力范围内的某一部分正确路径，同时抑制了其他（可能包含正确解的）探索路径。

3.3 困惑度分析 (Perplexity Analysis)

为了验证 RLVR 生成的路径是否"新颖"，作者计算了 Base 模型对 RLVR 生成内容的困惑度（PPL）：

• RLVR 生成的回答在 Base 模型中的 PPL 分布位于较低的区间。
• 这表明 RLVR 生成的内容本质上是 Base 模型本身就大概率会生成的模式。RLVR 主要是锐化（Sharpening）了 Base 模型的先验分布，而非拓展它。

3.4 与蒸馏 (Distillation) 的对比

与 RLVR 不同，使用 DeepSeek-R1 对 Qwen 进行蒸馏训练的模型，其 pass@k 曲线在所有 k k k 值下都显著高于 Base 模型。

• 结论：蒸馏通过引入教师模型的知识，确实扩展了模型的推理边界，而当前的 RLVR 仅是在优化现有边界内的搜索策略。

---

4. 算法与训练动力学分析

4.1 采样效率差距 ( Δ S E \Delta_{SE} ΔSE)

作者提出了 Sampling Efficiency Gap ( Δ S E \Delta_{SE} ΔSE) 指标，定义为 RL 模型的 pass@1 与 Base 模型 pass@256（作为能力上界代理）之间的差值。

• 测评了 PPO, GRPO, Reinforce++, RLOO, ReMax, DAPO 等算法。
• 结果 ：所有算法的 Δ S E \Delta_{SE} ΔSE 都很大（超过 40%），且算法间差异不本质。这说明现有 RL 算法在挖掘基座模型潜力方面远未达到最优 。

4.2 训练过程中的退化

随着 RL 训练步数的增加：

1. pass@1 持续上升（平均性能变好）。
2. pass@256 持续下降（推理能力边界收缩）。

• 这证实了 RLVR 是通过牺牲多样性和潜在的推理路径来换取特定路径的高概率输出。

---

5. 结论与启示

5.1 为什么 RLVR 没有带来新能力？

作者认为主要原因在于 LLM 的动作空间（Action Space）过于庞大，且 RLVR 高度依赖 Base 模型的预训练先验（Pretrained Priors）。

• 在如此巨大的空间中，盲目探索极难获得正反馈。
• RL 算法倾向于利用 Base 模型已有的高概率路径（Exploitation），而非探索未知的、可能正确但概率较低的路径（Exploration），导致模型被"困"在基座模型的先验中。

5.2 未来方向

为了真正解锁 RL 在 LLM 上的潜力，论文建议关注以下方向：

1. 高层抽象探索 (High-level Abstraction)：在程序或思维链的更高层级进行探索，而非 Token 级别。
2. 课程学习 (Curriculum)：通过从易到难的数据构建，分层减少探索空间。
3. 过程奖励 (Process Reward)：引入细粒度的中间反馈，而非仅依赖最终答案的二元奖励。
4. Agentic RL：引入多轮交互和环境反馈，允许模型在交互中获取新信息。

---

Gated Attention for Large Language Models: Non-linearity, Sparsity, and Attention-Sink-Free

1. 摘要

本研究系统地调查了在大语言模型（LLM）的 Softmax Attention 机制中引入门控（Gating） 的影响。通过在 15B MoE 模型和 1.7B Dense 模型上进行的超过 30 种变体的广泛实验（训练数据达 3.5T tokens），作者发现了一个简单但极其有效的修改方案：在 Scaled Dot-Product Attention (SDPA) 输出后应用 Head-Specific 的 Sigmoid 门控。

该机制不仅显著提升了模型性能（PPL 和下游任务），还带来了训练稳定性的提升（支持更大的学习率），并消除了"注意力汇聚（Attention Sink）"现象，从而增强了长上下文的外推能力。

---

2. 研究背景与动机

尽管门控机制在 LSTM、GRU、Gated Linear Attention 等架构中广泛应用，但在标准的 Softmax Attention（Transformer）中，其具体作用往往被忽略或与其他设计（如 MoE 路由、稀疏注意力）混淆 。

• 解耦需求：现有的如 Switch Heads 或 Native Sparse Attention 等工作虽然使用了门控，但未能将其效果与路由或稀疏设计剥离开来。
• 核心问题：本研究旨在通过控制变量法，探究在标准 Attention 层的不同位置引入门控的具体收益和内在机理 。

---

3. 方法论：门控注意力层 (Gated Attention Layer)

作者在标准 Multi-Head Attention 的计算流程中引入了门控操作 Y ′ = Y ⊙ σ ( X W θ ) Y' = Y \odot \sigma(X W_\theta) Y′=Y⊙σ(XWθ) 。

3.1 探索的设计空间

研究团队考察了五个维度的变体 ：

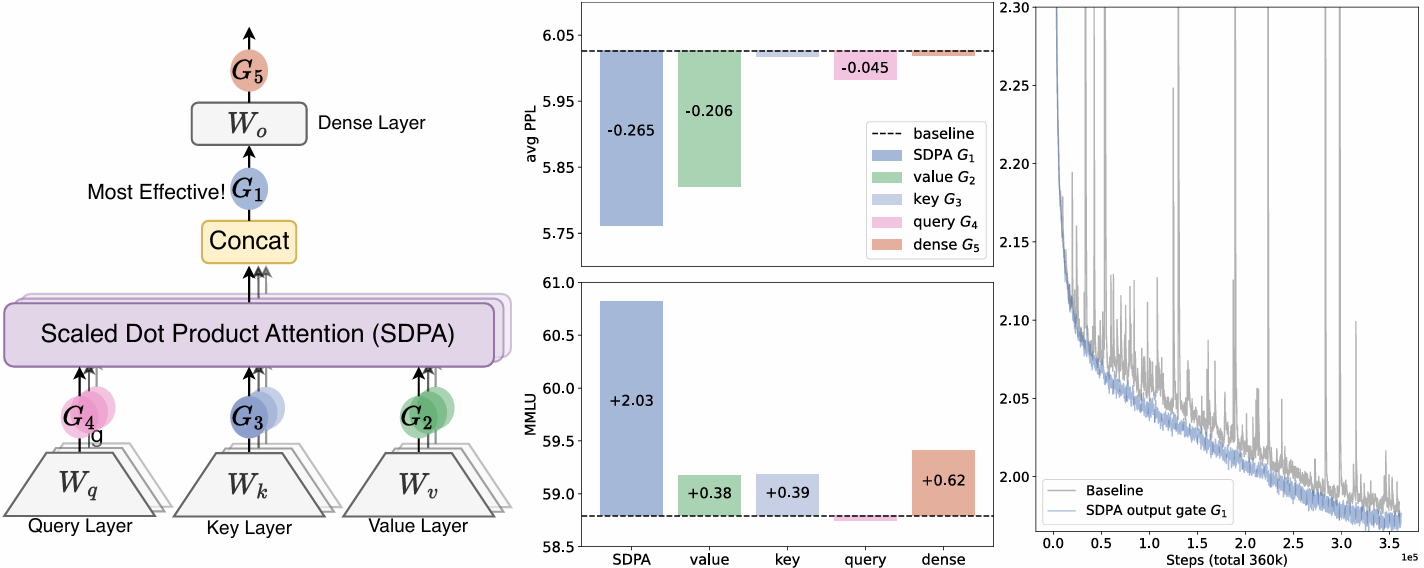
1. 位置 (Positions) ：
   • G 4 , G 3 , G 2 G_4, G_3, G_2 G4,G3,G2：分别位于 Query, Key, Value 投影之后。
   • G 1 G_1 G1 (关键)：位于 SDPA 输出之后（即 Softmax 归一化并加权求和后的结果）。
   • G 5 G_5 G5：位于最终输出层（Dense Output）之后。
2. 粒度 (Granularity)：Headwise（每头一个标量） vs. Elementwise（逐元素向量）。
3. 共享机制 (Sharing)：Head-Specific（每头独立参数） vs. Head-Shared（跨头共享）。
4. 计算方式 (Type)：乘法门控 (Multiplicative) vs. 加法门控 (Additive)。
5. 激活函数 (Activation)：Sigmoid vs. SiLU 等。

3.2 最佳实践结论

实验表明，SDPA 输出后的逐元素门控（Elementwise Gating at SDPA Output, G 1 G_1 G1） 是最佳配置。

• 公式表示 ：
  O = Concat ( Head 1 , ... , Head h ) W O O = \text{Concat}(\text{Head}_1, \dots, \text{Head}_h)W_O O=Concat(Head1,...,Headh)WO
  其中 Head i = Attention ( Q i , K i , V i ) ⊙ σ ( X i W θ i ) \text{Head}i = \text{Attention}(Q_i, K_i, V_i) \odot \sigma(X_i W{\theta_i}) Headi=Attention(Qi,Ki,Vi)⊙σ(XiWθi)。

---

4. 实验结果与性能分析

4.1 模型性能提升

• MoE 模型 (15B) ：在 400B token 上训练后，应用 G 1 G_1 G1 门控使 PPL 降低了约 0.265，MMLU 提升了 2.03 分，优于单纯增加参数量（如增加 Expert 数量或 Head 数量）的基线。
• Dense 模型 (1.7B)：在 3.5T token 的大规模训练中，门控带来的收益在不同学习率和 Batch Size 下保持一致。

4.2 训练稳定性 (Training Stability)

• 消除 Loss Spikes：引入门控后，训练过程中的 Loss 震荡（Spikes）几乎被消除。
• 支持更大的学习率：Baseline 模型在 8e-3 的学习率下会发散，而加了门控的模型可以稳定训练并获得更好收敛。

---

5. 机理分析：为什么门控有效？

论文通过深入分析，将收益归因于两个核心因素：非线性 (Non-linearity) 和 稀疏性 (Sparsity)。

5.1 非线性增强低秩映射

在标准 Attention 中，Value 投影 ( W V W_V WV) 和输出投影 ( W O W_O WO) 是连续的线性层。由于 d k < d m o d e l d_k < d_{model} dk<dmodel，这实际上构成了一个低秩线性映射。

• 发现 ：在 W V W_V WV 和 W O W_O WO 之间引入非线性（即门控）可以提高表达能力。
• 证据：即使只在 SDPA 输出后加一个无参的 RMSNorm（引入非线性），PPL 也能显著下降，证明了非线性的重要性。

5.2 引入输入依赖的稀疏性 (Input-Dependent Sparsity)

• 稀疏的门控分数：实验观察到，训练后的 Sigmoid 门控值高度集中在 0 附近（均值约为 0.116），这为 Attention 输出引入了极强的稀疏性 。
• 依赖 Query 的重要性：SDPA 后的门控是基于当前 Query 的输出计算的，而 Value 后的门控是基于 Value 计算的。实验证明前者效果更好，说明根据当前 Query 动态过滤信息至关重要 。
• 消融实验：如果强行使用 Non-Sparse Sigmoid（将值域限制在 [0.5, 1]），性能收益会大幅下降 。

5.3 消除 Attention Sink (Attention-Sink-Free)

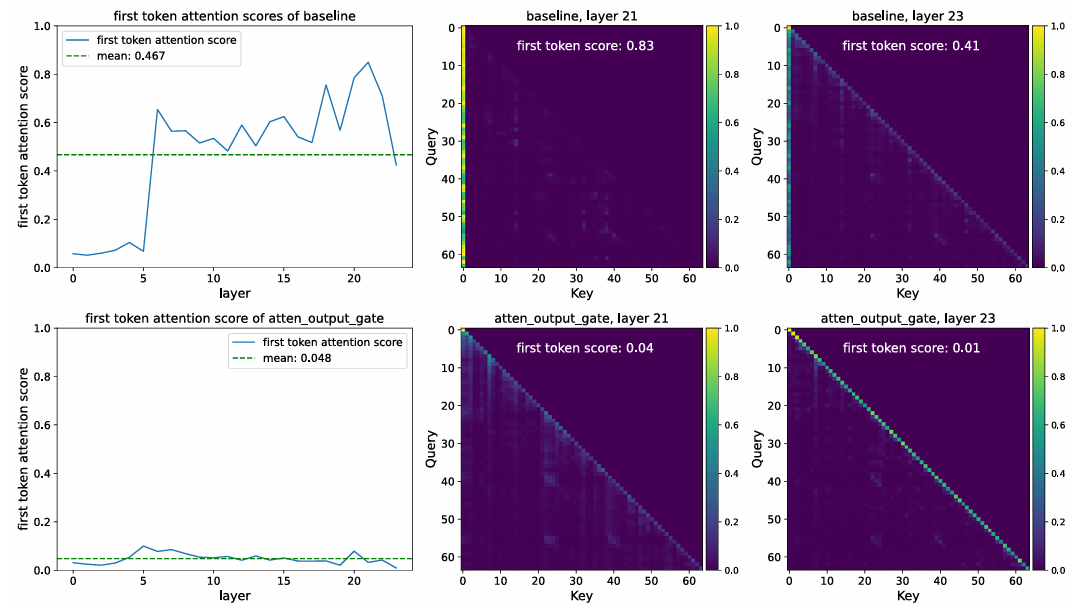
• 现象：标准 LLM 通常会将大量注意力分数分配给第一个 Token（Attention Sink），即便它没有语义意义 。
• 门控的作用：引入 SDPA 门控后，模型能够通过门控值"关掉"无关信息的流动。实验显示，加了门控的模型，首个 Token 的注意力占比从 46.7% 降至 4.8% 。
• 长上下文外推：由于消除了 Attention Sink，模型在通过 YaRN 进行上下文扩展（从 32k 扩展到 128k）时，表现显著优于 Baseline（RULER 基准测试提升 10+ 分） 。

---

6. 结论

本论文通过严谨的实证研究证明，在 Attention 机制中（特别是 SDPA 输出位置）引入简单的 Sigmoid 门控，是一种低成本、高收益的架构改进。它通过引入非线性和输入依赖的稀疏性，解决了低秩瓶颈和 Attention Sink 问题，显著提升了 LLM 的训练稳定性与长文本能力。

下一步建议：

如果您正在训练或微调 LLM，可以尝试在 Attention 层引入该门控机制，特别是在追求长上下文能力或遇到训练 Loss 震荡时。