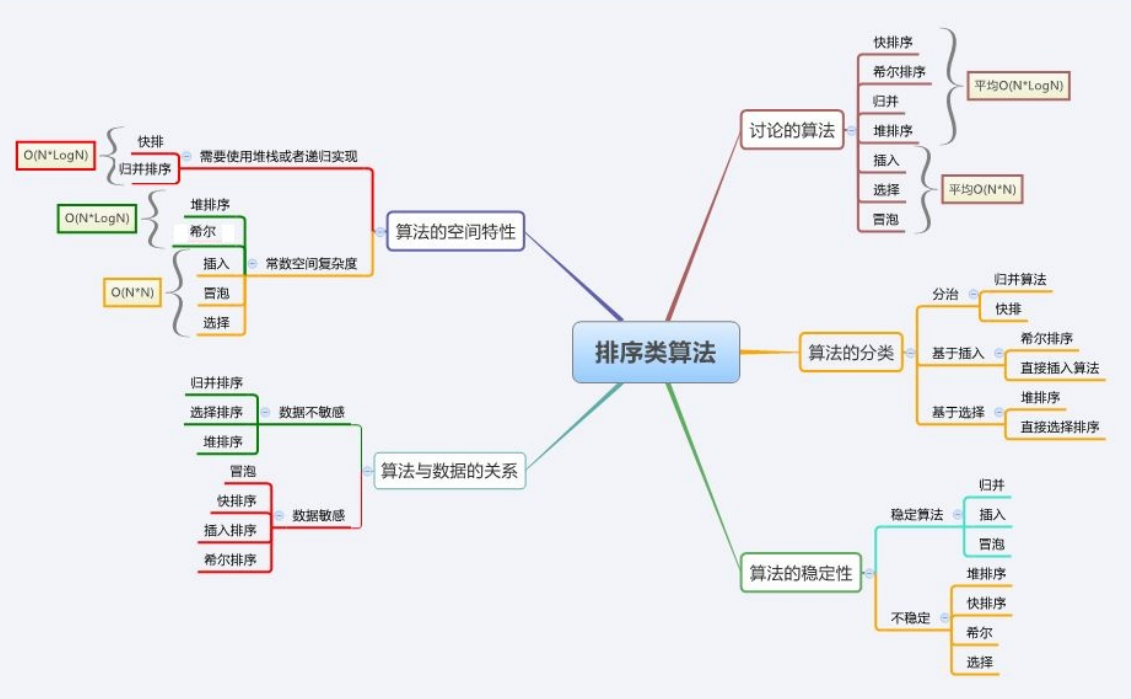
一.排序的概念及其运用

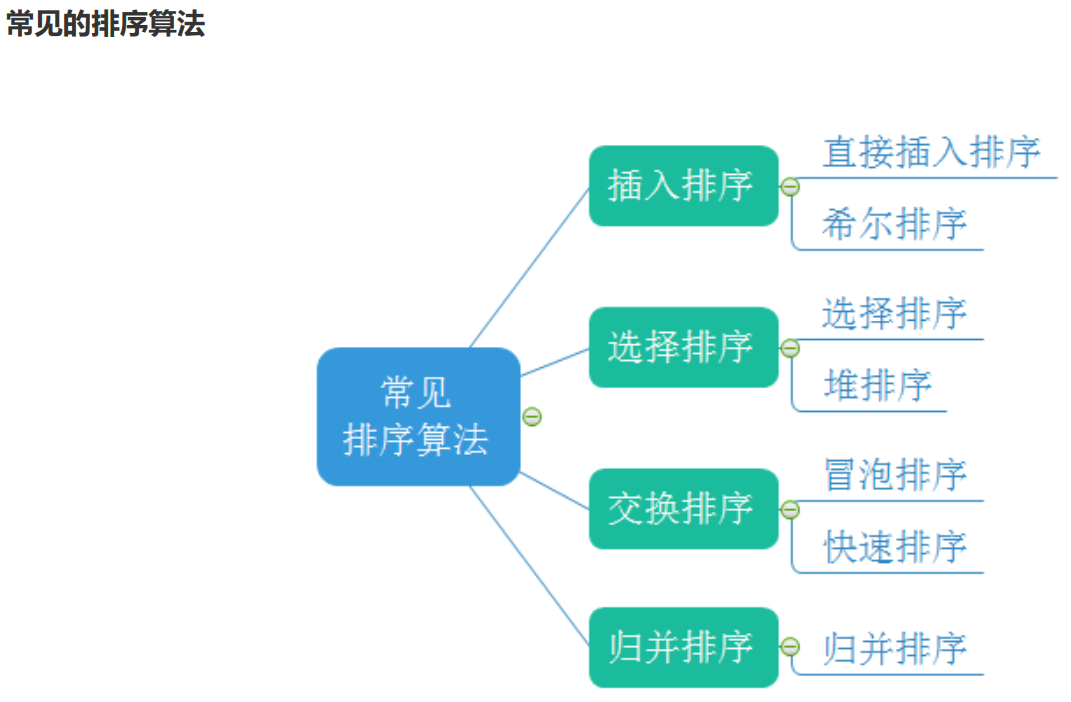
二.常见排序算法的实现
1.插入排序
a.直接插入排序

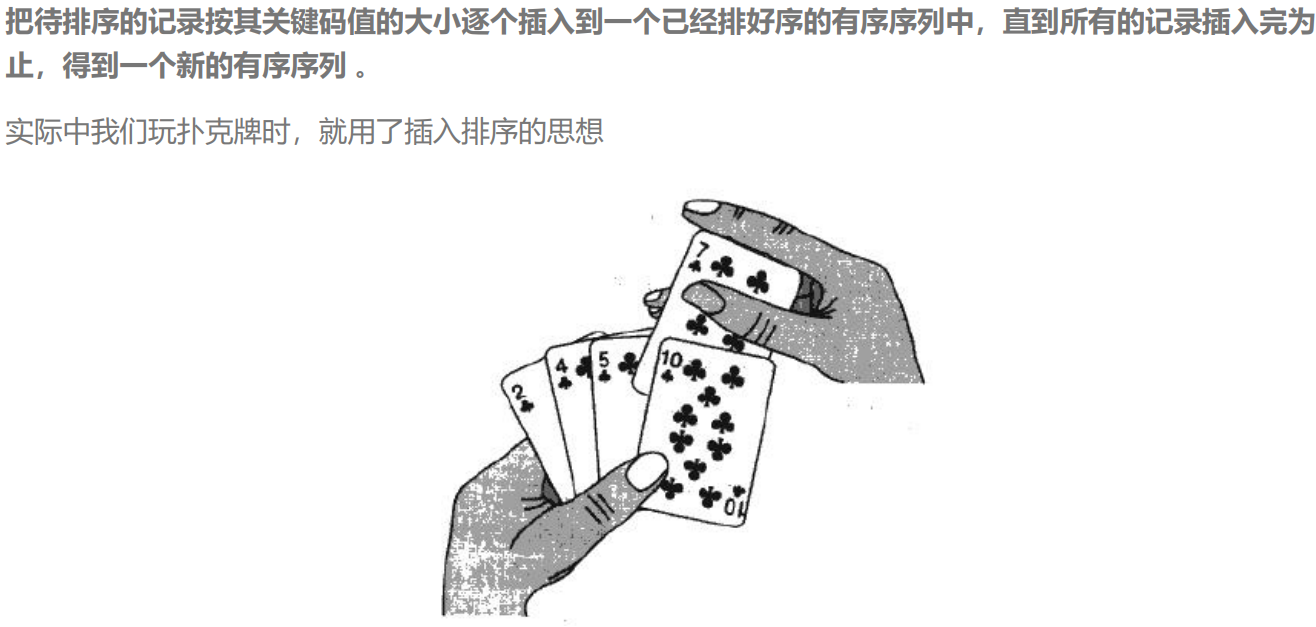

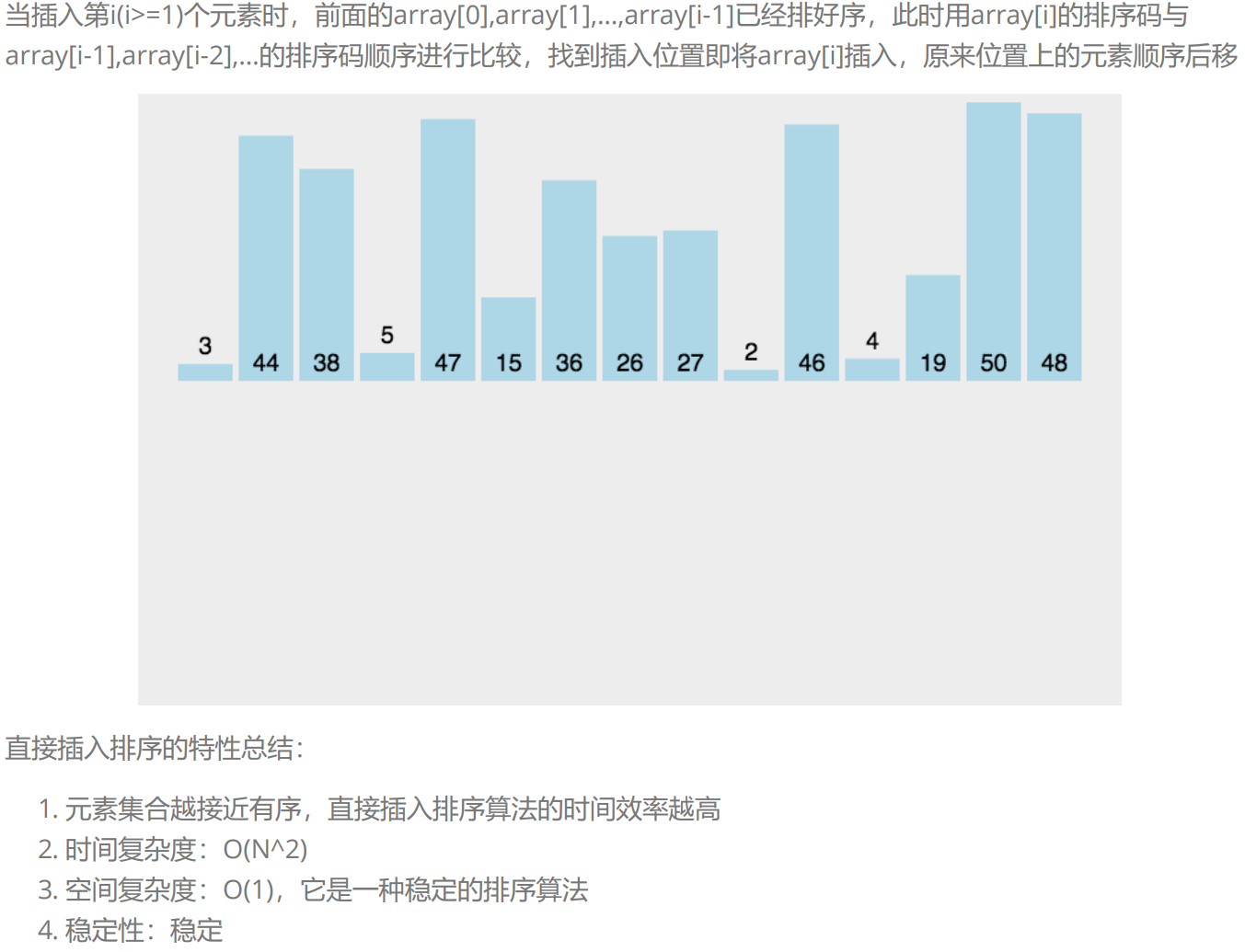
从后往前,一直比较,大就往前走,小就放
cpp
// 时间复杂度 O(N^2)
// 最坏情况:逆序
// 最好情况是多少:顺序有序或者接近有序 O(N)
void InsertSort(int* a, int n)
{
for (int i = 0; i < n-1; i++)
{
// [0, end] end+1
int end = i;
int tmp = a[end + 1];
while (end >= 0)
{
if (tmp < a[end])
{
a[end + 1] = a[end];
--end;
}
else
{
break;
}
}
a[end + 1] = tmp;
}
}b.希尔排序


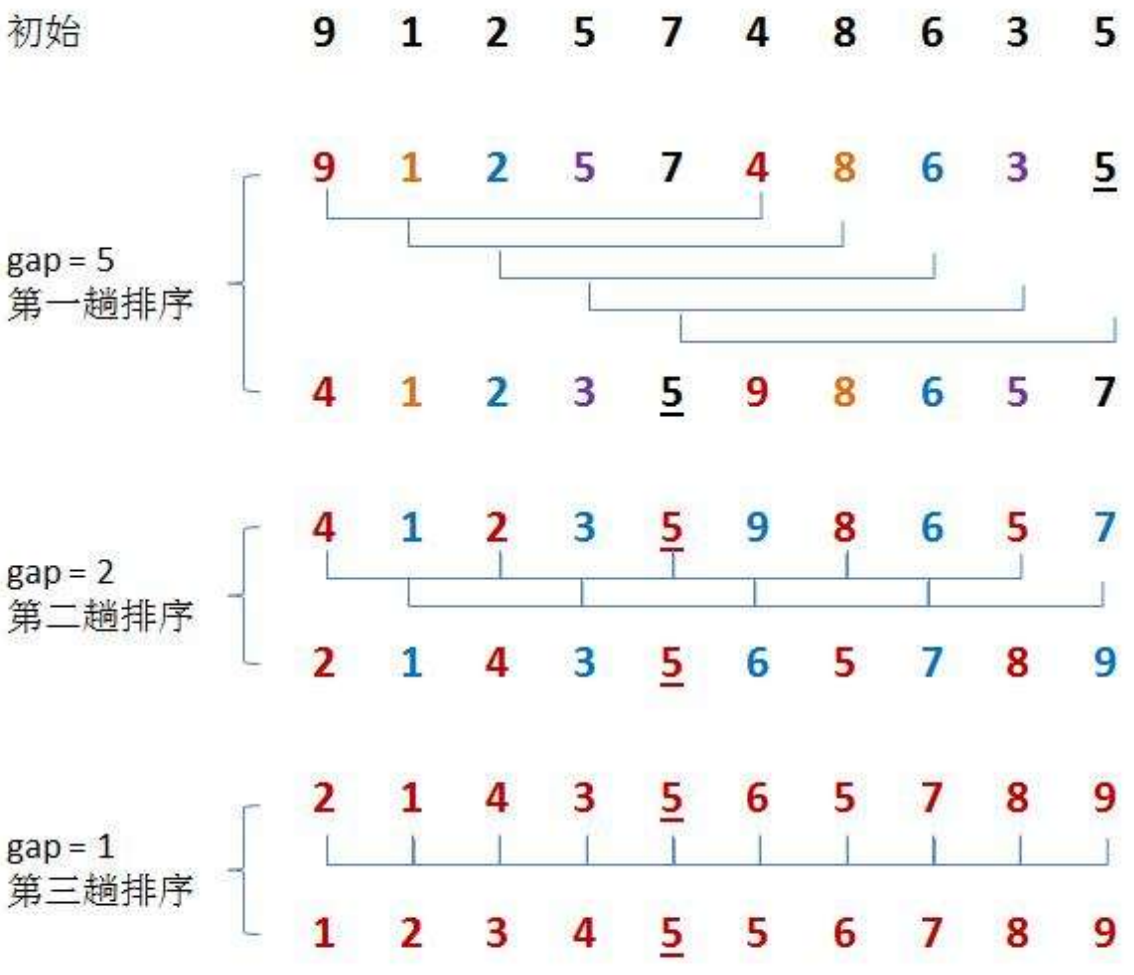


一次性跳跃 gap 次,让其变成相对有序的
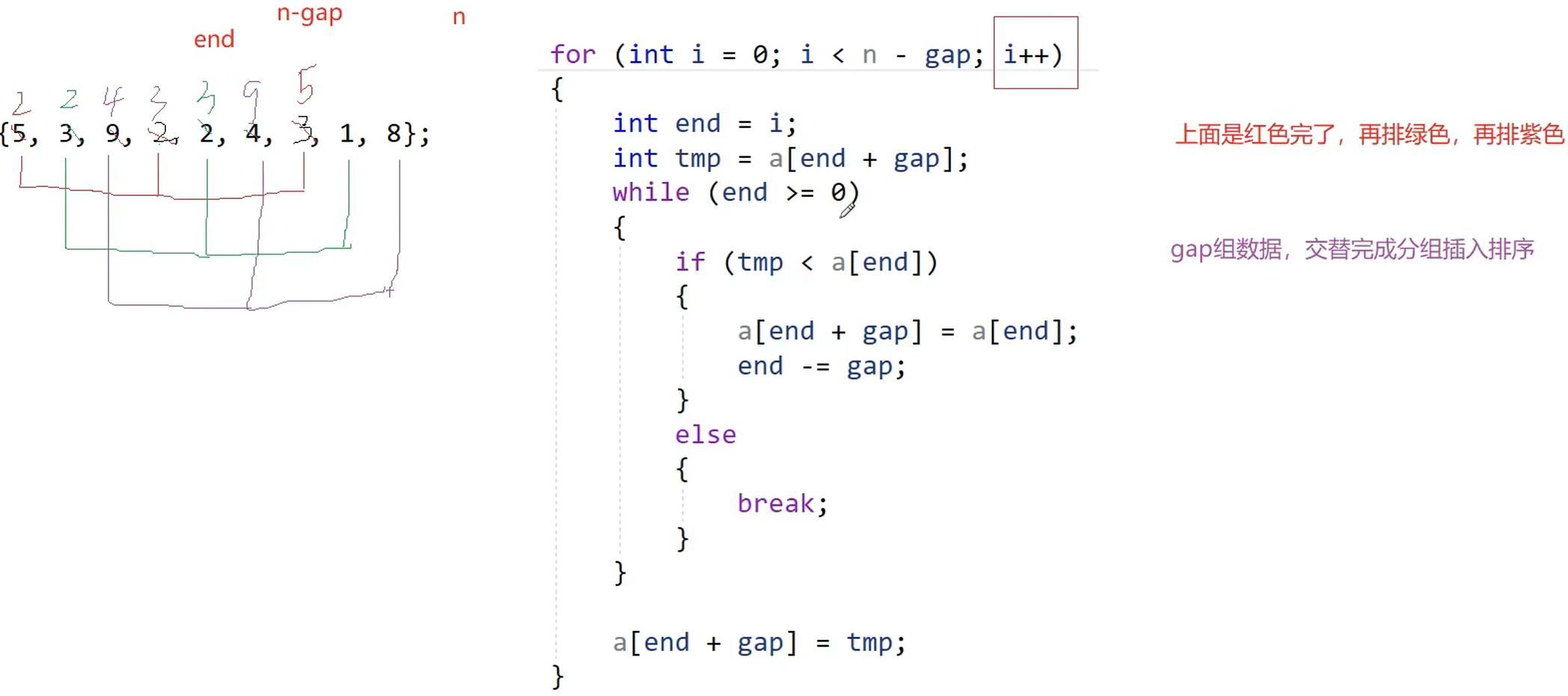

cpp
// 预排序 -- 目标:接近有序 gap > 1
// 插入排序 -- 目标:有序 gap == 1
void ShellSort(int* a, int n)
{
int gap = n;
while (gap > 1)
{
//gap /= 2;
gap = gap/3 + 1;
for (int i = 0; i < n - gap; i++)
{
int end = i;
int tmp = a[end + gap];
while (end >= 0)
{
if (tmp < a[end])
{
a[end + gap] = a[end];
end -= gap;
}
else
{
break;
}
}
a[end + gap] = tmp;
}
//PrintArray(a, n);
}
}这里我们的gap / 3 + 1更好,这里就不进行证明了(时间复杂度O(n ^ 1.3) 大致比n * log n略大)
2.选择排序

a.直接选择排序(直接遍历所有的数,选择最小的)
cpp
void SelectSort(int* a, int n)
{
int begin = 0, end = n - 1;
while (begin < end)
{
// 选出最小值和最大值的位置
int mini = begin, maxi = begin;
for (size_t i = begin + 1; i <= end; i++)
{
if (a[i] < a[mini])
{
mini = i;
}
if (a[i] > a[maxi])
{
maxi = i;
}
}
Swap(&a[begin], &a[mini]);
if (maxi == begin)
{
maxi = mini;
}
Swap(&a[end], &a[maxi]);
++begin;
--end;
//PrintArray(a, n);
}
}b.堆排序

cpp
void AdjustDown(int* a, int n, int parent)
{
int child = parent * 2 + 1;
while (child < n)
{
// 假设法,选出左右孩子中小的那个孩子
if (child + 1 < n && a[child + 1] < a[child])
{
++child;
}
if (a[child] < a[parent])
{
Swap(&a[child], &a[parent]);
parent = child;
child = parent * 2 + 1;
}
else
{
break;
}
}
}
// 升序,建大堆还是小堆呢?大堆
// O(N*logN)
void HeapSort(int* a, int n)
{
// a数组直接建堆 O(N)
for (int i = (n - 1 - 1) / 2; i >= 0; --i)
{
AdjustDown(a, n, i);
}
// O(N*logN)
int end = n - 1;
while (end > 0)
{
Swap(&a[0], &a[end]);
AdjustDown(a, end, 0);
--end;
}
}
3.交换排序

a.冒泡排序
cpp
// 时间复杂度 O(N^2)
// 最好情况是多少:顺序有序或者接近有序 O(N)
void BubbleSort(int* a, int n)
{
for (int j = 0; j < n-1; j++)
{
int exchange = 0;
for (int i = 1; i < n-j; i++)
{
if (a[i - 1] > a[i])
{
Swap(&a[i - 1], &a[i]);
exchange = 1;
}
}
if (exchange == 0)
break;
}
}
n * log n 的排序时间,差距就非常大了

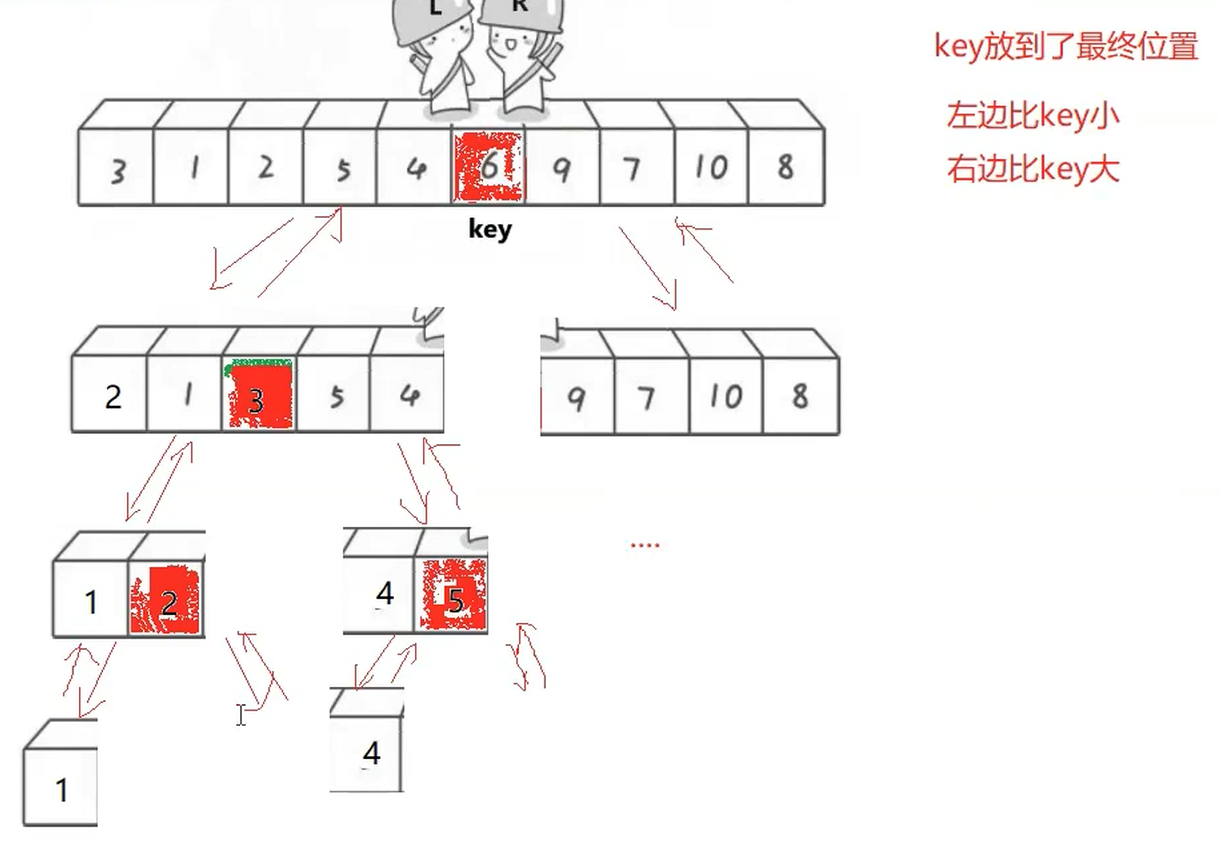
b.快速排序


a.hoare版本
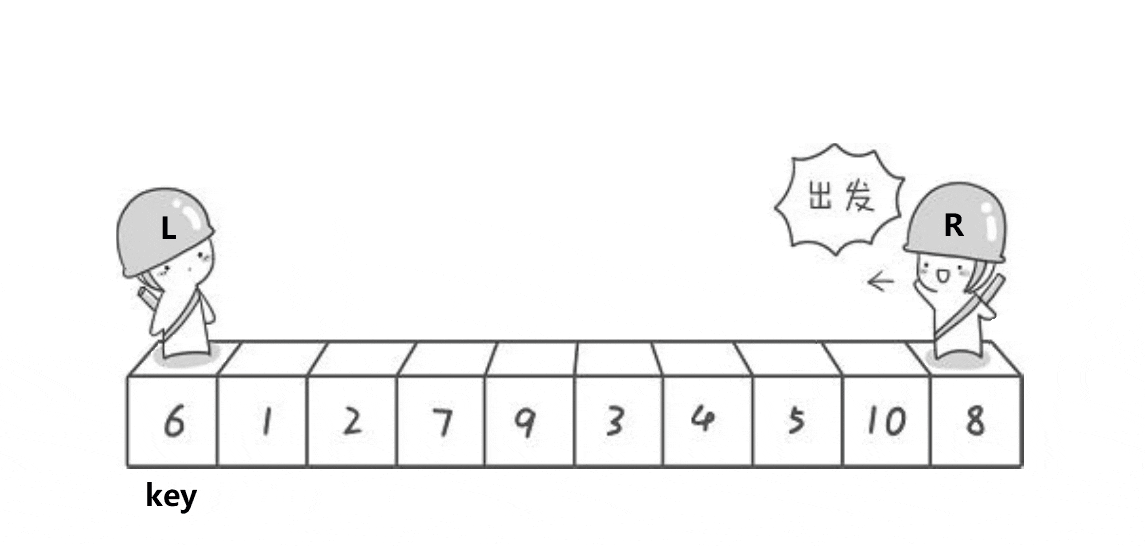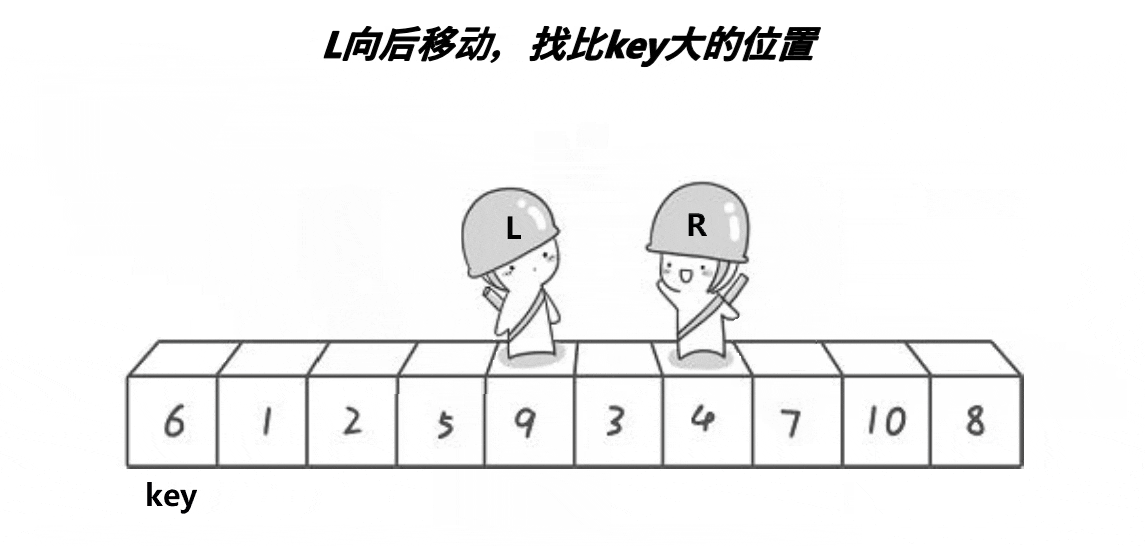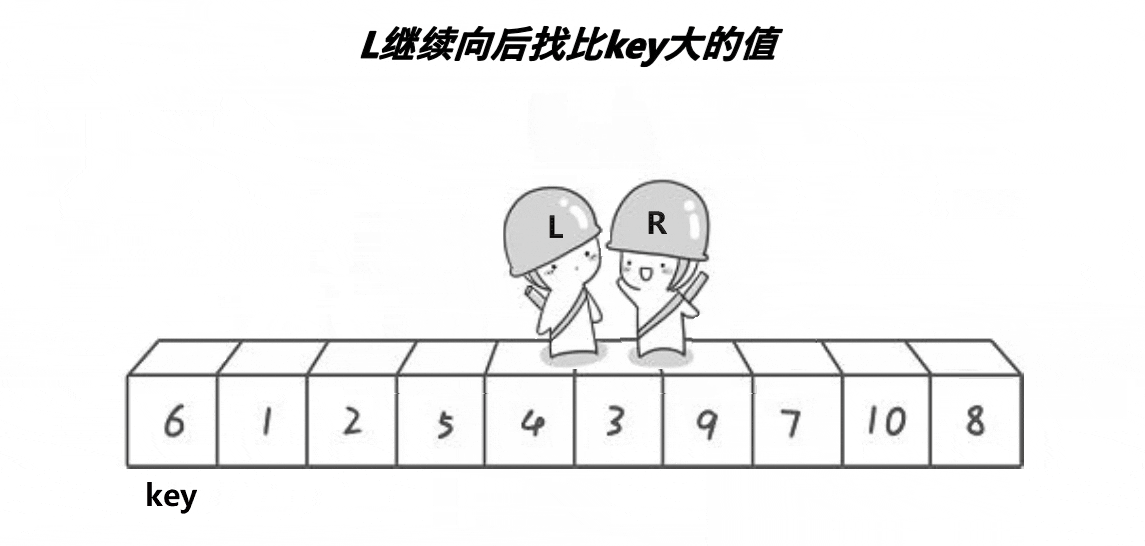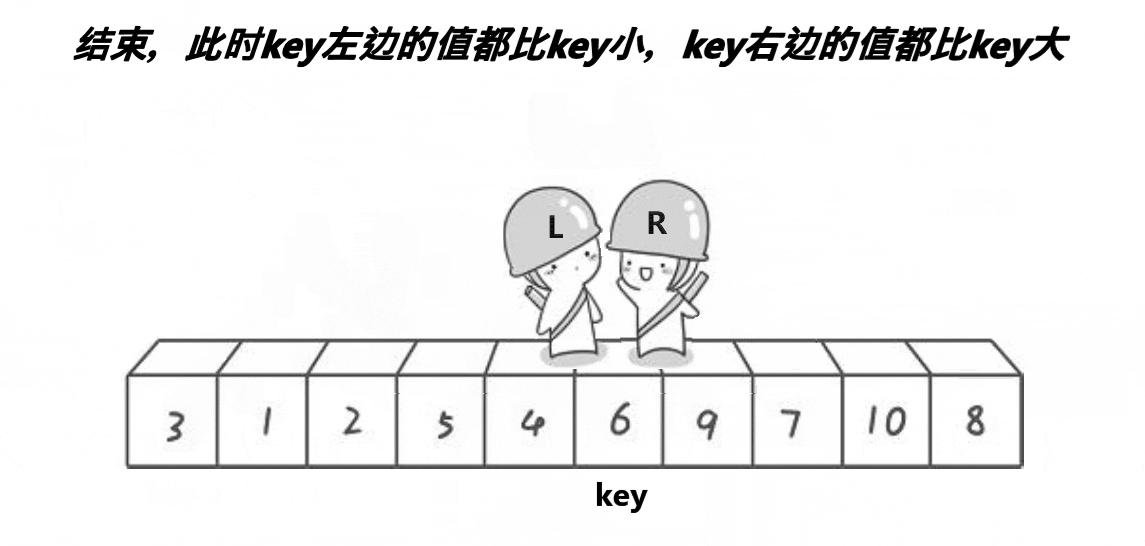
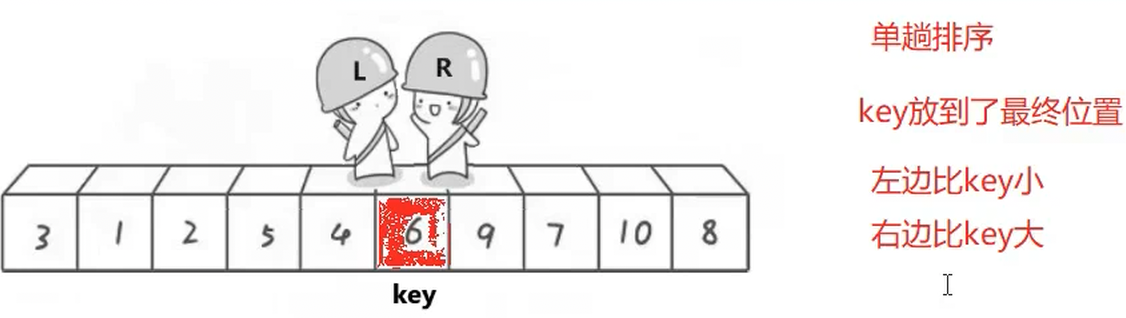
然后我们再排序 左子树 和 右子树 ,等拍好了就全部都排序好了
cpp
void QuickSort(int* a, int left, int right)
{
// 区间只有一个值或者不存在就是最小子问题
if (left >= right)
return;
int begin = left, end = right;
int keyi = left;
while (left < right)
{
// right先走,找小
while (left < right && a[right] >= a[keyi])
{
--right;
}
// left再走,找大
while (left < right && a[left] <= a[keyi])
{
++left;
}
Swap(&a[left], &a[right]);
}
Swap(&a[left], &a[keyi]);
keyi = left;
// [begin, keyi-1]keyi[keyi+1, end]
QuickSort(a, begin, keyi - 1);
QuickSort(a, keyi+1, end);
}

所以,右边先走会保证至少是等于key
如果是有序的(接近有序),那么快速排序就很慢,时间复杂度是O(N ^ 2)

随机数选key
cpp
void QuickSort(int* a, int left, int right)
{
if(left >= right)
{
return;
}
int begin = left,end = right;
int randi = rand();
randi %= (right - left);
randi += left;
Swap(&a[left],&a[randi]);
int keyi = left;
while(left < right)
{
while(left < right && a[right] >= a[keyi])
{
--right;
}
while(left < right && a[left] <= a[keyi])
{
++left;
}
Swap(&a[left],&a[right]);
}
Swap(&a[left],&a[keyi]);
keyi = left;
QuickSort(a,begin,keyi - 1);
QuickSort(a,keyi + 1,end);
}三数取中(这个较好)
cpp
// 三数取中 left mid right
// 大小居中的值,也就是不是最大也不是最小的
int GetMidi(int* a, int left, int right)
{
int mid = (left + right) / 2;
if (a[left] < a[mid])
{
if (a[mid] < a[right])
{
return mid;
}
else if (a[left] > a[right])
{
return left;
}
else
{
return right;
}
}
else // a[left] > a[mid]
{
if (a[mid] > a[right])
{
return mid;
}
else if (a[left] < a[right])
{
return left;
}
else
{
return right;
}
}
}
void QuickSort(int* a, int left, int right)
{
if(left >= right)
{
return;
}
int begin = left,end = right;
int midi = GetMidi(a,left,right);
Swap(&a[left],&a[midi]);
int keyi = left;
while(left < right)
{
while(left < right && a[right] >= a[keyi])
{
--right;
}
while(left < right && a[left] <= a[keyi])
{
++left;
}
Swap(&a[left],&a[right]);
}
Swap(&a[left],&a[keyi]);
keyi = left;
QuickSort(a,begin,keyi - 1);
QuickSort(a,keyi + 1,end);
}两种排序合并实现排序(减少递归调用的栈的消耗)
后面小区间,走我们的插入排序,大区间走快排
cpp
void QuickSort1(int* a, int left, int right)
{
// 区间只有一个值或者不存在就是最小子问题
if (left >= right)
return;
// 小区间选择走插入,可以减少90%左右的递归
if (right - left + 1 < 10)
{
InsertSort(a + left, right - left + 1);
}
else
{
int begin = left, end = right;
// 三数取中
int midi = GetMidi(a, left, right);
//printf("%d\n", midi);
Swap(&a[left], &a[midi]);
int keyi = left;
while (left < right)
{
// right先走,找小
while (left < right && a[right] >= a[keyi])
{
--right;
}
// left再走,找大
while (left < right && a[left] <= a[keyi])
{
++left;
}
Swap(&a[left], &a[right]);
}
Swap(&a[left], &a[keyi]);
keyi = left;
// [begin, keyi-1]keyi[keyi+1, end]
QuickSort1(a, begin, keyi - 1);
QuickSort1(a, keyi + 1, end);
}
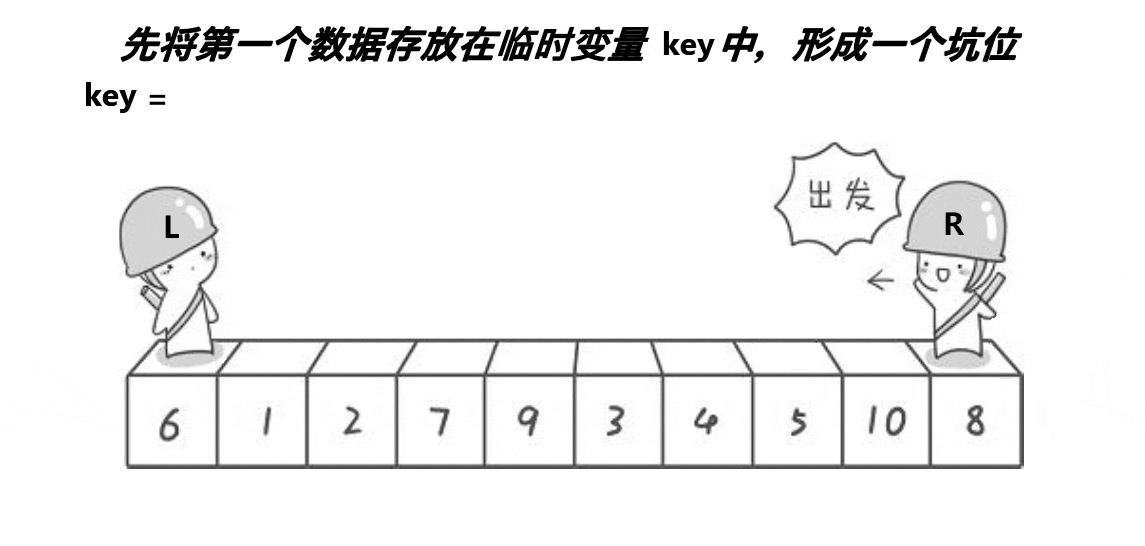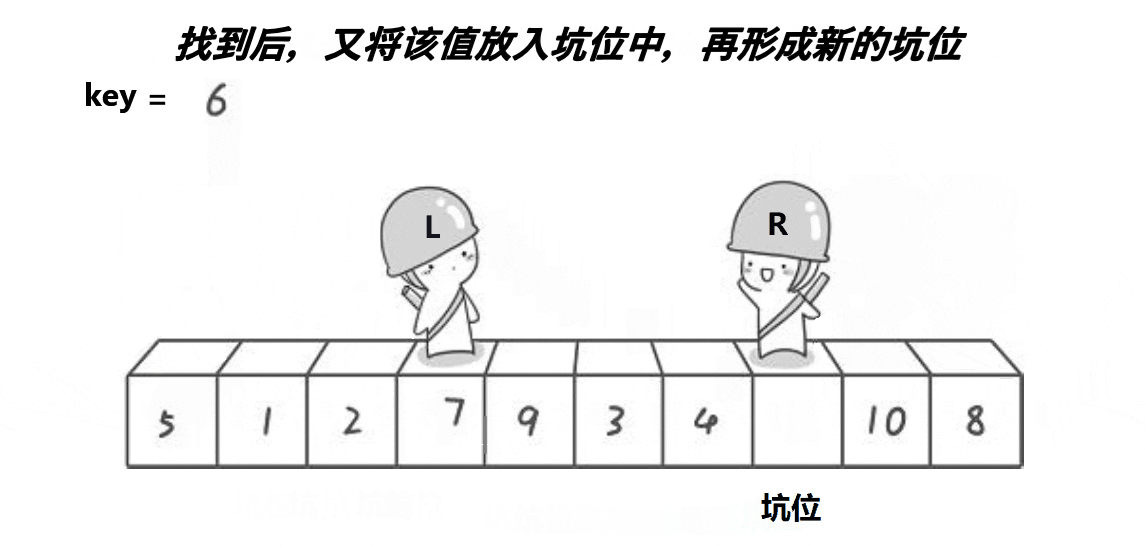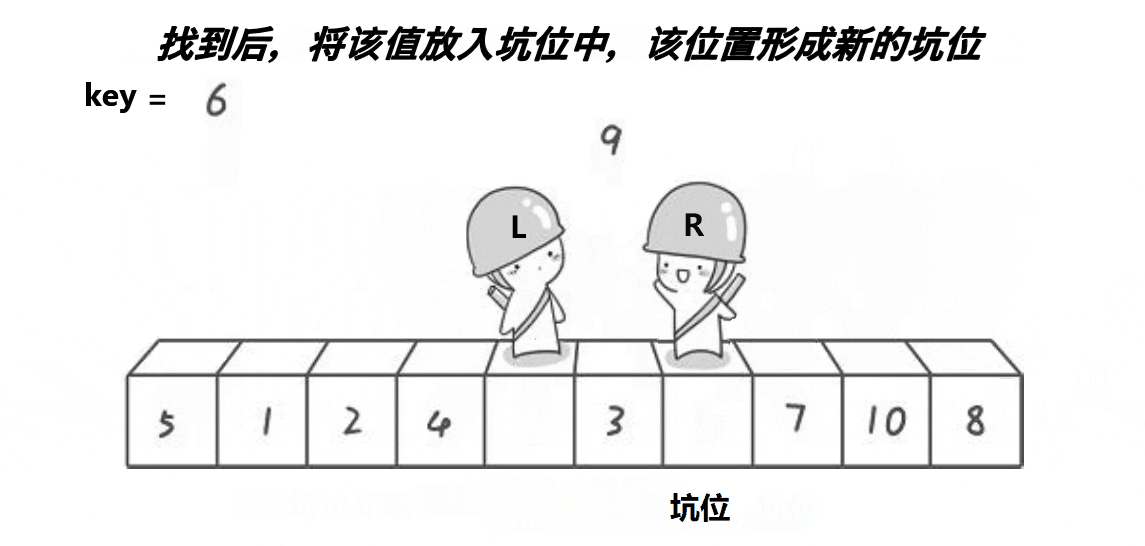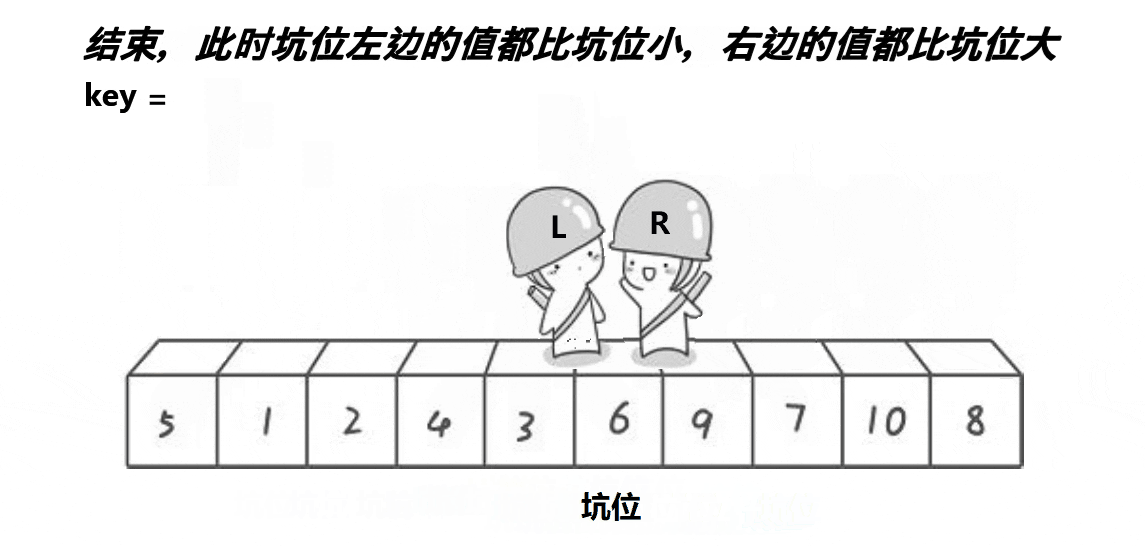
}b.挖坑法版本
cpp
// 挖坑法划分
int partion(int* array, int begin, int end) {
int key = array[begin]; // 选取第一个数为基准值
while (begin < end) {
while (begin < end && array[end] >= key) // 从后向前找第一个小于基准值的数
end--;
array[begin] = array[end]; // 放到begin位置
while (begin < end && array[begin] <= key) // 从前向后找第一个大于基准值的数
begin++;
array[end] = array[begin]; // 放到end的位置
}
array[begin] = key; // 将基准值放入该位置
return begin; // 返回当前基准值的位置,以便递归划分
}
// 快速排序函数
void quicksort(int* array, int begin, int end) {
if (begin >= end)
return;
int keypos = partion(array, begin, end);
quicksort(array, begin, keypos - 1);
quicksort(array, keypos + 1, end);
}c.前后指针版本
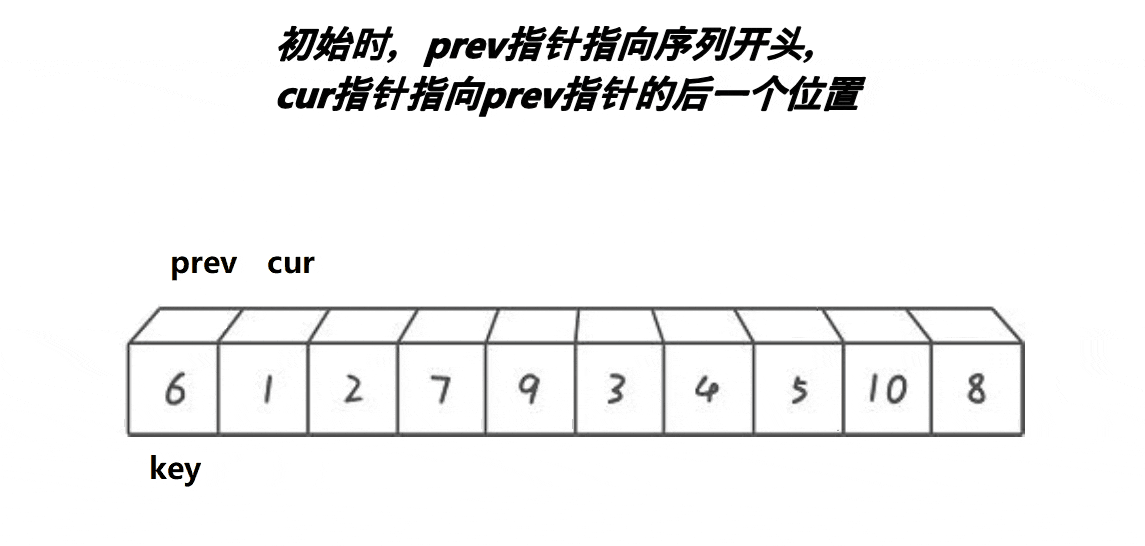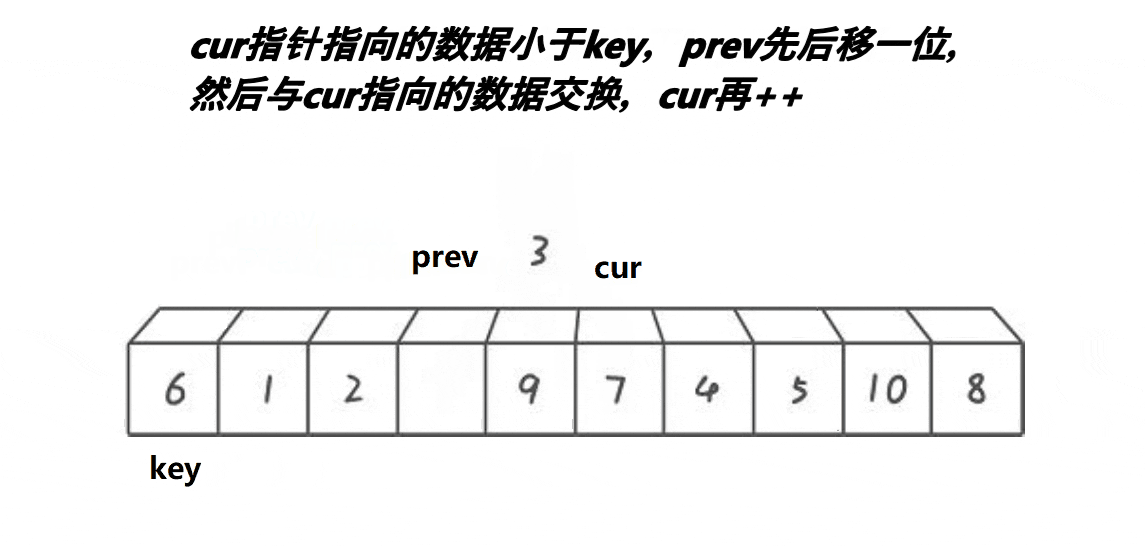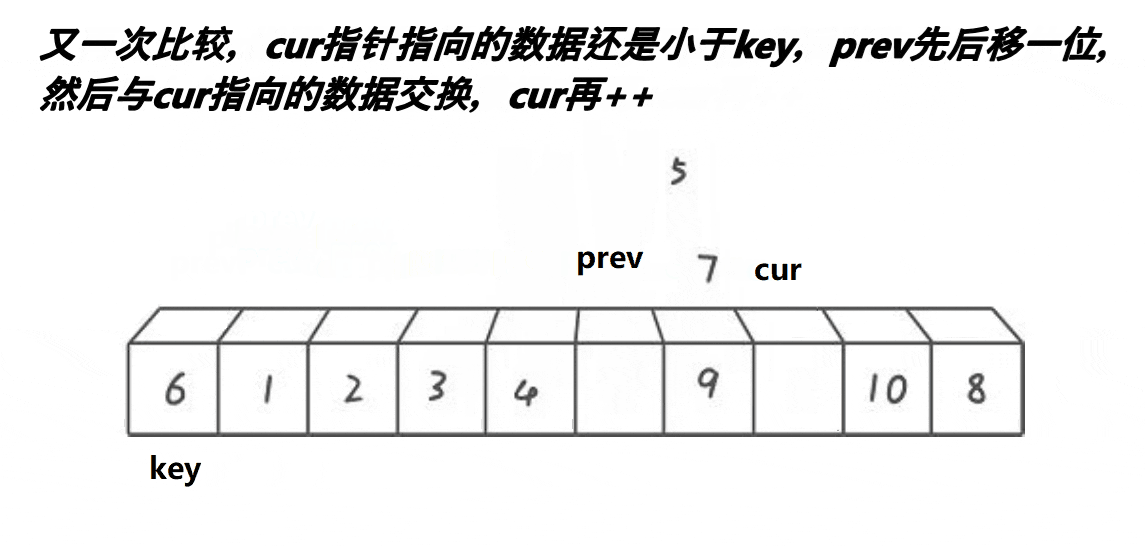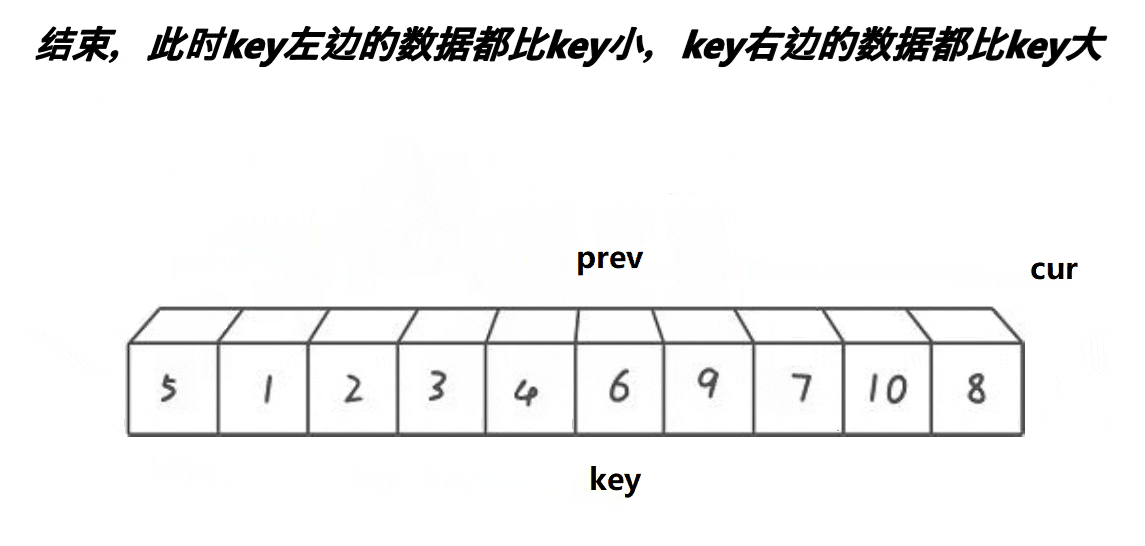

cpp
void QuickSort(int* a, int left, int right)
{
if (left >= right)
return;
int keyi = left;
int prev = left;
int cur = left+1;
while (cur <= right)
{
if (a[cur] < a[keyi] && ++prev != cur)
Swap(&a[prev], &a[cur]);
++cur;
}
Swap(&a[keyi], &a[prev]);
keyi = prev;
// [left, keyi-1]keyi[keyi+1, right]
QuickSort(a, left, keyi - 1);
QuickSort(a, keyi + 1, right);
}d.非递归版本
一般,我们使用递归,消耗的是栈帧(栈空间),而我们使用stack,是在堆空间上开辟空间
cpp
void QuickSortNonR(int* a, int left, int right)
{
ST st;
STInit(&st);
STPush(&st, right);
STPush(&st, left);
while (!STEmpty(&st))
{
int begin = STTop(&st);
STPop(&st);
int end = STTop(&st);
STPop(&st);
// 单趟
int keyi = begin;
int prev = begin;
int cur = begin + 1;
while (cur <= end)
{
if (a[cur] < a[keyi] && ++prev != cur)
Swap(&a[prev], &a[cur]);
++cur;
}
Swap(&a[keyi], &a[prev]);
keyi = prev;
// [begin, keyi-1] keyi [keyi+1, end]
if (keyi + 1 < end)
{
STPush(&st, end);
STPush(&st, keyi + 1);
}
if (begin < keyi-1)
{
STPush(&st, keyi-1);
STPush(&st, begin);
}
}
STDestroy(&st);
}
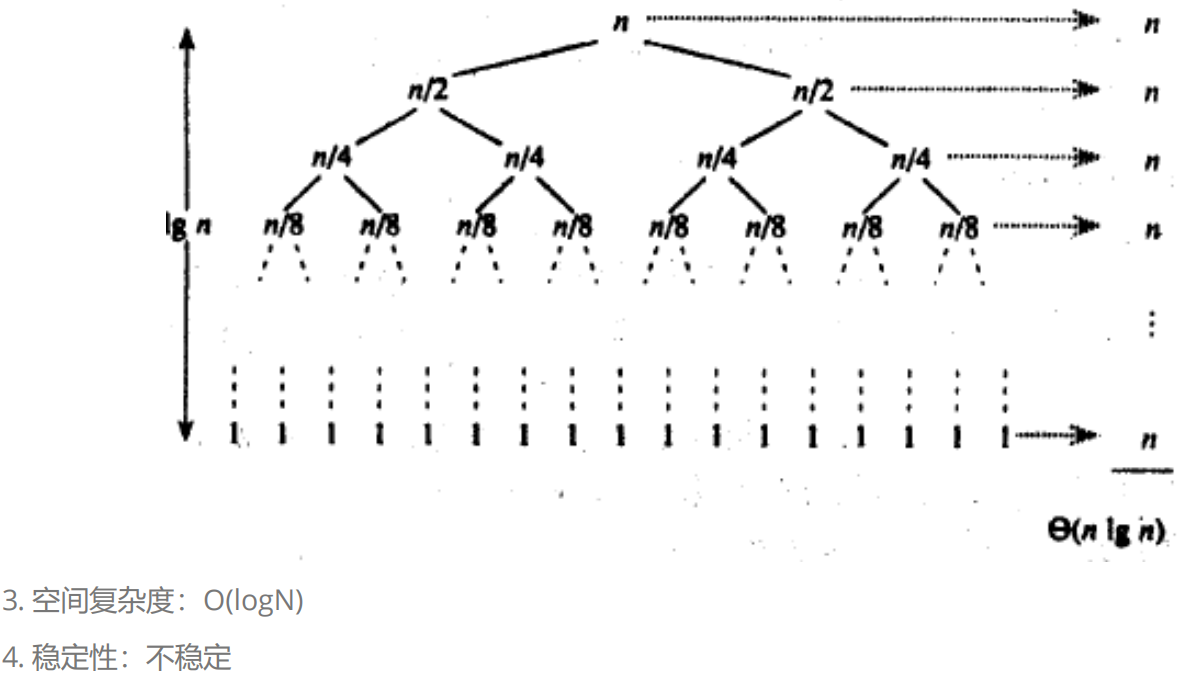
4.归并排序

a.递归实现
cpp
void _MergeSort(int* a, int begin, int end, int* tmp)
{
if (begin == end)
return;
int mid = (begin + end) / 2;
// [begin, mid] [mid+1, end]
_MergeSort(a, begin, mid, tmp);
_MergeSort(a, mid+1, end, tmp);
// 归并
int begin1 = begin,end1 = mid;
int begin2 = mid + 1,end2 = end;
int i = begin;
// 依次比较,取小的尾插tmp数组
while (begin1 <= end1 && begin2 <= end2)
{
if (a[begin1] <= a[begin2])
{
tmp[i++] = a[begin1++];
}
else
{
tmp[i++] = a[begin2++];
}
}
while (begin1 <= end1)
{
tmp[i++] = a[begin1++];
}
while (begin2 <= end2)
{
tmp[i++] = a[begin2++];
}
memcpy(a + begin, tmp + begin, sizeof(int) * (end - begin + 1));
}
void MergeSort(int* a, int n)
{
int* tmp = (int*)malloc(sizeof(int) * n);
if (tmp == NULL)
{
perror("malloc fail");
return;
}
_MergeSort(a, 0, n-1, tmp);
free(tmp);
tmp = NULL;
}b.非递归实现
cpp
void MergeSortNonR(int* a, int n)
{
int* tmp = (int*)malloc(sizeof(int) * n);
if (tmp == NULL)
{
perror("malloc fail");
return;
}
int gap = 1;
while (gap < n)
{
//printf("gap:%d->", gap);
for (int j = 0; j < n; j += 2 * gap)
{
int begin1 = j, end1 = begin1 + gap - 1;
int begin2 = begin1 + gap, end2 = begin2 + gap - 1;
//printf("[%d,%d][%d,%d] ", begin1, end1, begin2, end2);
// 越界的问题处理
if (end1 >= n || begin2 >= n)
break;
if (end2 >= n)
end2 = n - 1;
int i = j;
// 依次比较,取小的尾插tmp数组
while (begin1 <= end1 && begin2 <= end2)
{
if (a[begin1] <= a[begin2])
{
tmp[i++] = a[begin1++];
}
else
{
tmp[i++] = a[begin2++];
}
}
while (begin1 <= end1)
{
tmp[i++] = a[begin1++];
}
while (begin2 <= end2)
{
tmp[i++] = a[begin2++];
}
memcpy(a + j, tmp + j, sizeof(int) * (end2-j+1));
}
//printf("\n");
gap *= 2;
}
free(tmp);
tmp = NULL;
}三.非比较排序


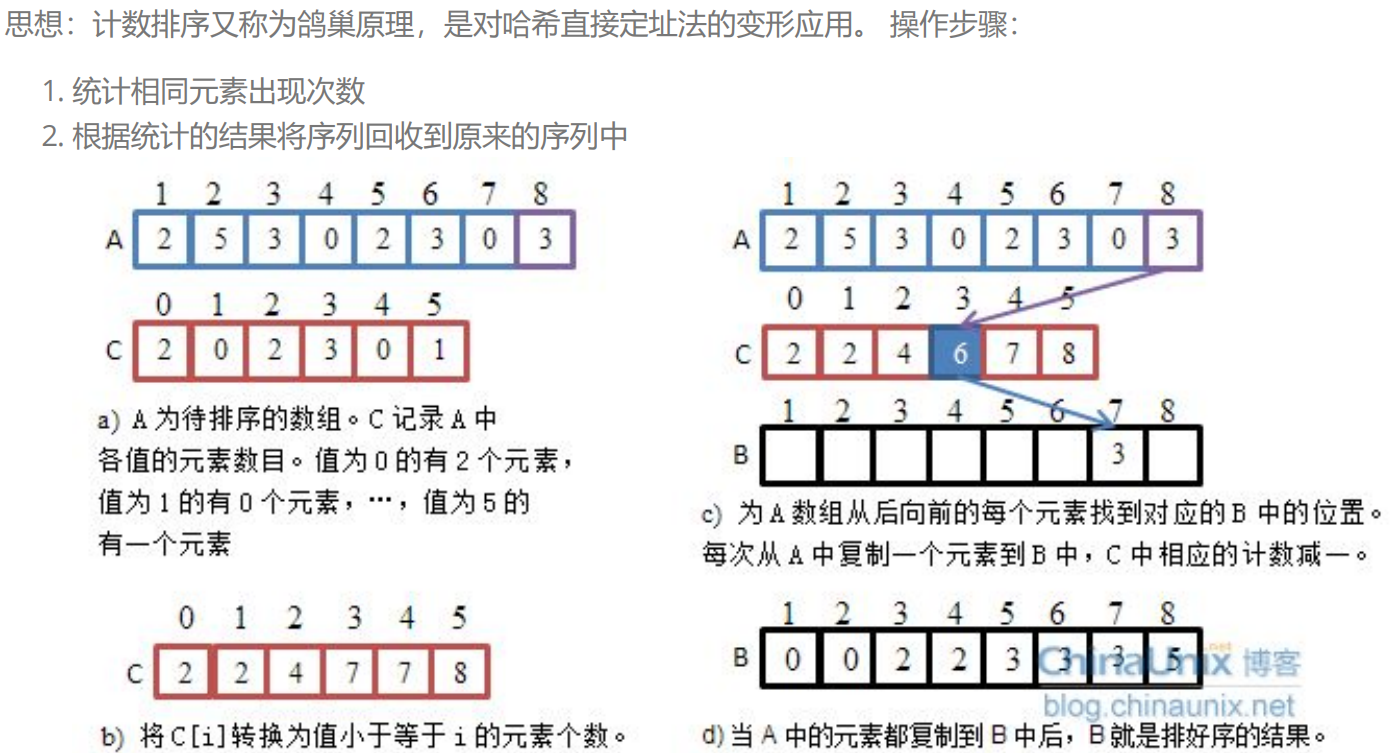
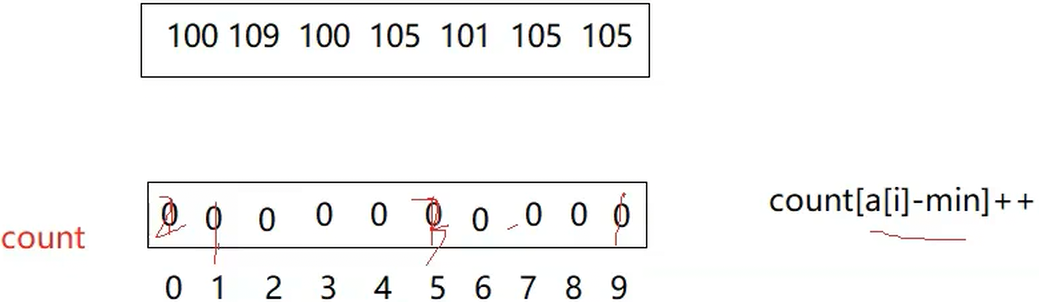


cpp
// 时间复杂度:O(N+range)
// 空间复杂度:O(range)
void CountSort(int* a, int n)
{
int min = a[0], max = a[0];
for (int i = 1; i < n; i++)
{
if (a[i] > max)
max = a[i];
if (a[i] < min)
min = a[i];
}
int range = max - min + 1;
int* count = (int*)malloc(sizeof(int) * range);
if (count == NULL)
{
perror("malloc fail");
return;
}
memset(count, 0, sizeof(int) * range);
// 统计次数
for (int i = 0; i < n; i++)
{
count[a[i] - min]++;
}
// 排序
int j = 0;
for (int i = 0; i < range; i++)
{
while (count[i]--)
{
a[j++] = i + min;
}
}
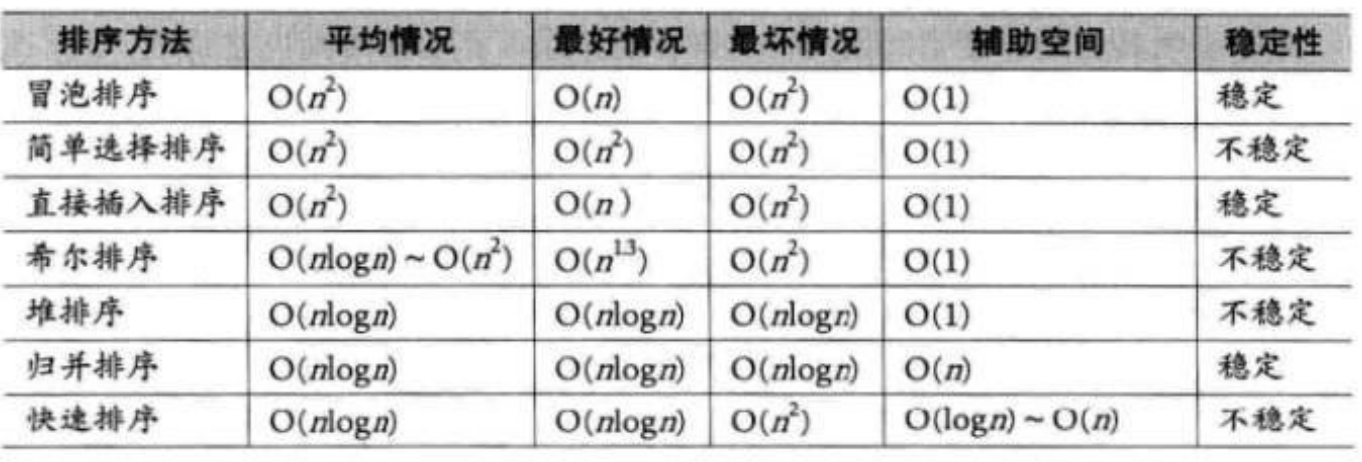
}四.排序算法复杂度及稳定性分析