目录
写在前面:* 代表是重点内容
1.树的相关术语
- 根节点、叶节点、分支节点
- 父节点:直接前驱,根节点没有父节点
- 孩子结点:直接后继,叶子结点没有孩子结点
- 结点的度:某一结点的孩子数量(如叶节点的度为0)
- 树的度:所有结点中,度的最大值
- 树的高度(深度):一共多少层
- 两个结点之间的最短路径:两个结点之间的最短路径(dfs求最短路径)
- 路径长度:两点的路径中,边的个数
2.算法竞赛树的常见形式
- 有序树(结点子树顺序从左往右的顺序)与无序树(没有顺序)
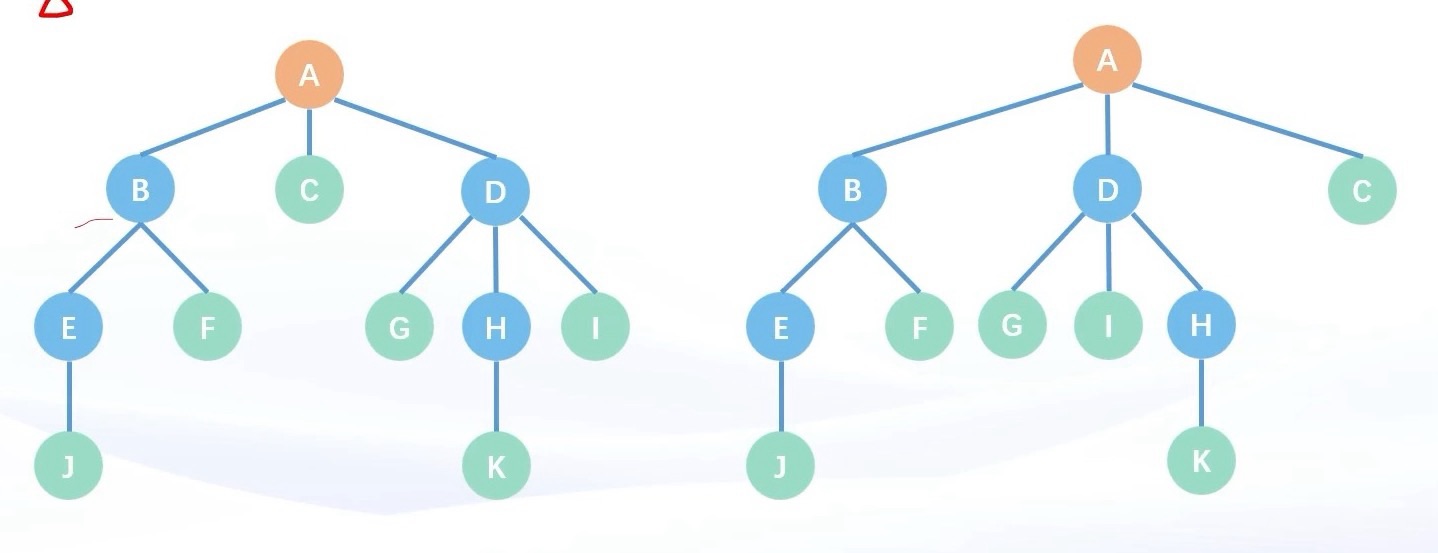
- 有根树(根节点明确)与无根树(根节点不明确,A、B、E任意一个结点都可以作为根节点)

3.*树的存储
孩子表示法:
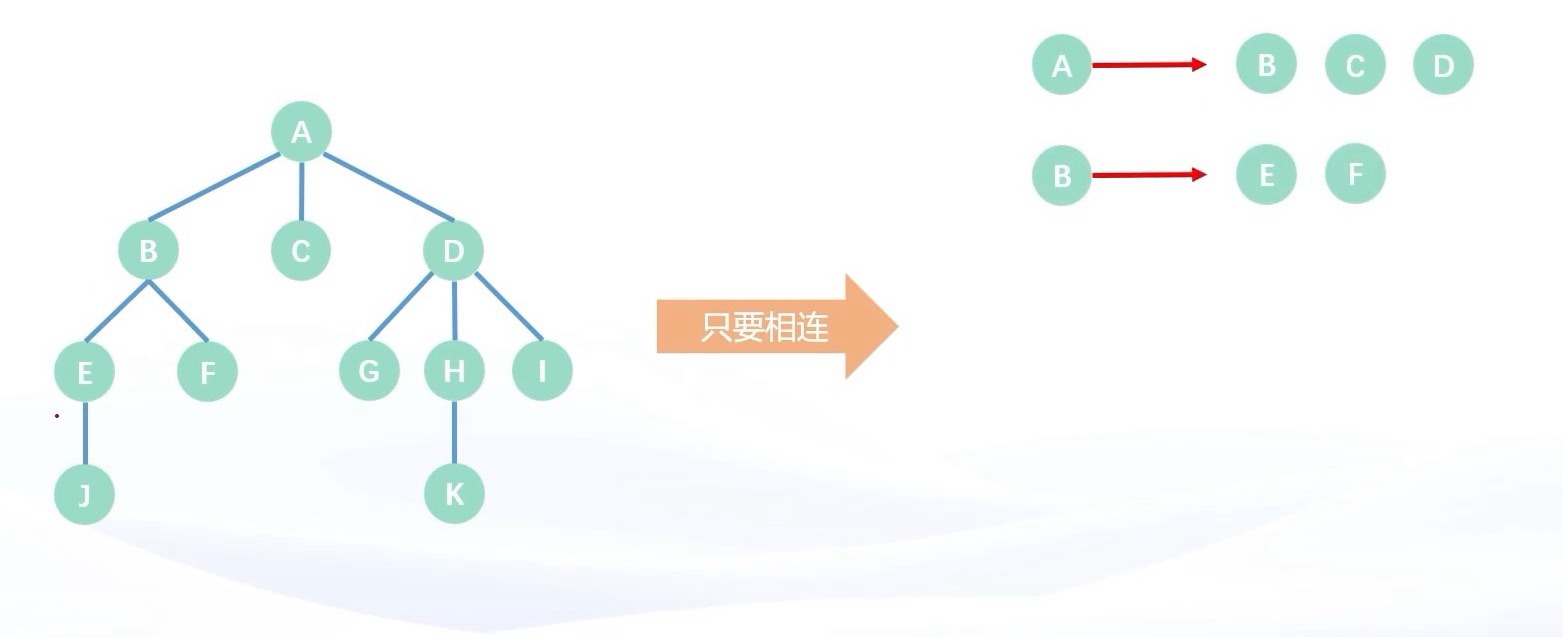
孩子表示法是对于每一个结点,只存储所有孩子的信息;例如A结点有 B、C、D 两个孩子结点,那么对于A结点就存储 BCD 这三个内容
问题在于,对于无根树那种父子关系不明确的树,无法肯定 BCD 和 A 的关系,那我们索性就把 ABCD 全都存储下来,即把结点与其相连的结点全都存储下来
孩子表示法的vector数组实现:
算法比赛中,一般给出的树结构都是用编号简化的,同时会提供下面两条信息:
- 结点的个数 n
- n - 1 条 x 结点与 y 结点相连的边
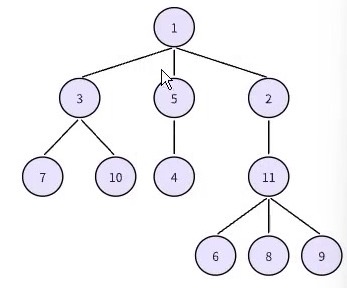
大致如下图所示(下图中虽然告知了根结点,但输入中没有说明父子关系,只讲了 x,y 之间有一条边,所以还是要当作无根树来处理)

代码实现:
- 创建一个大小足够的vector类型数组(不是创建一个vector),即 vector<int> edges[N] ;其中,edges[i] 存放了 i 结点的所有孩子
- 对于 i 的孩子,直接 edges[i].push_back 即可
- 如果是无根树,push_back 完 i 的孩子以后,还得把 i 也 push_back 到其孩子后,因为无法确定他们之间的父子关系
代码:
cpp
#include<iostream>
#include<vector>
using namespace std;
const int N = 1e5+10;//最多是10^5个结点
vector<int> edges[N];
int main()
{
int n;cin>>n;//多少个结点?
for(int i=1;i<n;i++)//n-1条边
{
int x,y;cin>>x>>y;
edges[x].push_back(y);
edges[y].push_back(x);
}
return 0;
}孩子表示法的链式前向星实现:
链式前向星的本质是用链表存储所有的孩子,其中链表是用数组模拟实现的。
相当于创建出 N 个链表,每个链表存储结点与其相连结点的信息。
代码实现:
- 创建一个足够大的数组 h,作为所有链表的头结点**( h[1] 即表示,以1号结点作为头结点的链表中头结点的下一个结点,可以视作表头元素)**
- 创建两个足够大的数组 e 和 ne,一个作为数据域,一个作为指针域
- 一个变量 id ,标记新来结点存储的位置
- 当 x 有一个孩子 y (即相邻且相连)时,就把 y 头插到 x 的链表中,然后再把 x 头插到 y 的链表中(无根树的原因,还得把 x 头插到 y 中)
- h[x] = y 相当于 x -> y (即在头插结束以后,把链表头结点也视作一个有效结点,并且该头结点一定是链表的表头)
- e数组、ne数组需要开 N(链表数量) 的 2 倍大小,因为就拿x、y举例,由于是静态链表,所以x存在y后需要占用一个空间,y存在x后需要占用一个空间
代码:
cpp
#include<iostream>
using namespace std;
const int N = 1e5+10;
int h[N],e[N*2],ne[N*2],id;//h[i]表示某个i结点作为头结点的链表中,表头元素
void push_front(int x,int y)
{
id++;
e[id]=y;
ne[id]=h[x];
h[x]=id;
}
int main()
{
int n;cin>>n;
for(int i=1;i<n;i++)
{
int x,y;cin>>x>>y;
//每次进行头插
push_front(x,y);
push_front(y,x);
}
return 0;
}4.*深度优先遍历(DFS)
深度优先遍历可以看作是对树进行一次前序遍历,前序遍历可以用递归的方式实现
代码实现:
- 创建一个函数dfs,并传入根节点
- 在函数中,访问当前结点
- 找到一个没有遍历过的孩子 v
- 递归调用 dfs 函数,从 v 走到 v 的孩子,然后把其孩子作为根节点
但是对于一棵无根树来说,上面的方法就会出现问题;如下图所示,当A递归调用到了B以后,因为A也有可能是B的孩子,所以B也会递归调用到A,然后无穷无尽无止境也;因此,我们需要标记哪些结点已经遍历过了,即在上述操作3之前加一步,标记当前结点已遍历
代码1(vector数组):
cpp
#include<iostream>
#include<vector>
using namespace std;
const int N = 1e5+10;
vector<int> edges[N];
bool vst[N];//判断结点是否访问过
void dfs(int root)
{
cout<<root<<" ";
vst[root]=true;
for(int i=0;i<edges[root].size();i++)
{
if(!vst[edges[root][i]])
{
dfs(edges[root][i]);
}
}
}
int main()
{
//创建树
int n;cin>>n;
for(int i=1;i<n;i++)
{
int x,y;cin>>x>>y;
edges[x].push_back(y);
edges[y].push_back(x);
}
dfs(1);
return 0;
}

代码2(链式前向星):
cpp
#include<iostream>
using namespace std;
const int N = 1e5+10;
int h[N],e[N*2],ne[N*2],id;//h[i]表示某个i结点作为头结点的链表中,表头元素
bool vst[N];
void push_front(int x,int y)
{
id++;
e[id]=y;
ne[id]=h[x];
h[x]=id;
}
void dfs(int root)
{
cout<<root<<" ";
vst[root]=true;
for(int i=h[root];i;i=ne[i])
//先找到根节点所在链表,然后遍历整个链表,找到还没访问过的结点
{
int val = e[i];
if(!vst[val])
{
dfs(val);
}
}
}
int main()
{
int n;cin>>n;
for(int i=1;i<n;i++)
{
int x,y;cin>>x>>y;
//每次进行头插
push_front(x,y);
push_front(y,x);
}
dfs(1);
return 0;
}

两种代码结果解释:
上面的两种代码,前一种是以根左右的方式输出的,后一种是以根右左的方式输出的,这是由于建树时的不同导致的;vector数组建树是把元素直接进行尾插操作,所以先输入的元素(即左边的元素)dfs遍历的时候先遍历到;链式前向星则是通过头插操作,所以越往后输入的元素dfs越是后遍历到,所以就有了根右左的效果
层序遍历时也一样,一个是从左往右,一个是从右往左
5.*宽度优先遍历(BFS)
宽度优先遍历可以看作是对树进行一次层序遍历,借助queue模板即可实现
代码实现:
- 创建一个队列,辅助bfs
- 根节点入队
- 若队列不为空,对头结点出队并访问该结点,然后将该结点的所有孩子依次根据从左到右的顺序入队
- 重复3过程,直到队列为空
- 为了解决父子关系不明确的问题,和dfs一眼也需要标记当前节点已遍历
代码1(vector数组):
cpp
#include<iostream>
#include<vector>
#include<queue>
using namespace std;
const int N = 1e5+10;
vector<int> edges[N];
bool vst[N];//判断结点是否访问过
void bfs()
{
queue<int> q;
q.push(1);
vst[1]=true;
while(q.size())
{
int val=q.front();q.pop();
cout<<val<<" ";
for(auto v:edges[val])
{
if(!vst[v])
{
q.push(v);
vst[v]=true;
}
}
}
}
int main()
{
//创建树
int n;cin>>n;
for(int i=1;i<n;i++)
{
int x,y;cin>>x>>y;
edges[x].push_back(y);
edges[y].push_back(x);
}
bfs();
return 0;
}
代码2(链式前向星):
cpp
#include<iostream>
#include<queue>
using namespace std;
const int N = 1e5+10;
int h[N],e[N*2],ne[N*2],id;//h[i]表示某个i结点作为头结点的链表中,表头元素
bool vst[N];
void push_front(int x,int y)
{
id++;
e[id]=y;
ne[id]=h[x];
h[x]=id;
}
void bfs()
{
queue<int> q;
//存入整棵树的根节点
q.push(1);
vst[1]=true;
while(q.size())
{
int val = q.front();q.pop();
cout<<val<<" ";
for(int i=h[val];i;i=ne[i])
{
int v = e[i];
if(!vst[v])
{
q.push(v);
vst[v]=true;
}
}
}
}
int main()
{
int n;cin>>n;
for(int i=1;i<n;i++)
{
int x,y;cin>>x>>y;
//每次进行头插
push_front(x,y);
push_front(y,x);
}
bfs();
return 0;
}
6.dfs与bfs的时空复杂度
dfs:
- 时间复杂度:n 个节点,n-1 条边,每条边遍历2次(无根树存两次),所以是2(n-1),即O(N)
- 空间复杂度:一棵树n个结点,最坏情况下可能要开n个函数栈帧(即一棵从上往下的链表一样的树),所以空间复杂度为 O(N)
bfs:
- 时间复杂度:n个结点,每个结点入队1次出队1次,为2n,即O(N)
- 空间复杂度:极端情况为根节点以后,其余结点都是根节点的孩子,此时队列大小为n-1,所以为O(N)
两者都是针对一棵先序遍历(根左右+根右左)建立起来的树进行操作,dfs即是用先序遍历的方法暴力搜索整棵树,bfs即是用层序遍历的方法暴力搜索整棵树