【数据结构】打破线性思维：树形结构与堆在C语言中的完美实现方案

🏠 个人主页: EXtreme35

📚 个人专栏:

专栏名称	专栏主题简述
《C语言》	C语言基础、语法解析与实战应用
《数据结构》	线性表、树、图等核心数据结构详解
《题解思维》	算法思路、解题技巧与高效编程实践

从树到堆：C语言数据结构深度实战教程
一、树------非线性结构的基石
- [1.1 树的严谨定义](#1.1 树的严谨定义)
- [1.2 树的定义与术语](#1.2 树的定义与术语)
- [1.3 树的复杂表示：孩子兄弟表示法](#1.3 树的复杂表示：孩子兄弟表示法)
二、二叉树------规则的艺术
- [2.1 二叉树的特殊规则](#2.1 二叉树的特殊规则)
- [2.2 两种特殊的二叉树（堆的物理基础）](#2.2 两种特殊的二叉树（堆的物理基础）)
- [2.3 二叉树的重要性质](#2.3 二叉树的重要性质)
三、从逻辑到物理------堆的数组映射
- [3.1 为什么堆使用顺序存储？](#3.1 为什么堆使用顺序存储？)
- [3.2 下标映射公式](#3.2 下标映射公式)
- [3.3 堆的定义](#3.3 堆的定义)
四、堆的底层原理与核心算法
- [4.1 核心算法一：上浮 (AdjustUP)](#4.1 核心算法一：上浮 (AdjustUP))
- [4.2 核心算法二：下沉 (AdjustDown)](#4.2 核心算法二：下沉 (AdjustDown))
五、堆的高级应用
- [5.1 堆排序 (Heap Sort)](#5.1 堆排序 (Heap Sort))
- [5.2 Top-K 问题（海量数据处理）](#5.2 Top-K 问题（海量数据处理）)
六、结语

从树到堆：C语言数据结构深度实战教程

前言：在计算机科学的浩瀚海洋中，数据结构是承载算法的基石。我们熟悉的数组和链表是线性的，它们简单直观，但在面对复杂的层级关系或特定的动态排序需求时，往往显得力不从心。本教程将带你从线性的世界迈入非线性的树（Tree）的世界，并最终聚焦于一种特殊的完全二叉树------堆（Heap）。

一、树------非线性结构的基石

在数组和链表的世界里，数据是一对一的线性关系。但在现实世界（如文件系统、组织架构）中，更多的是层次关系。

1.1 树的严谨定义

树是由 n ( n ≥ 0 ) n (n \ge 0) n(n≥0) 个有限结点组成的一个具有层次关系的集合。

递归定义 ：树中有一个特殊的结点称为根（Root） 。除根外，其余结点被分成 M ( M > 0 ) M (M>0) M(M>0) 个互不相交的集合 T 1 , T 2 , . . . , T m T_1, T_2, ..., T_m T1,T2,...,Tm，其中每一个集合又是一棵结构与树类似的子树。

注意：子树之间绝对不能相交，如果相交，那就变成了图（Graph）。

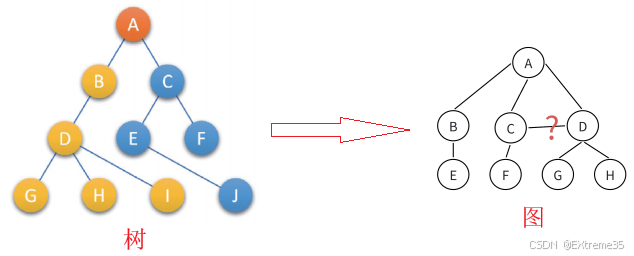
1.2 树的定义与术语

树（Tree） 是一种非线性的数据结构，它是由 n n n ( n ≥ 0 n \geq 0 n≥0) 个节点组成的有限集合。

如果 n = 0 n=0 n=0，它是一棵空树。
如果 n > 0 n>0 n>0，它有一个特定的节点被称为根（Root） ，其余节点被分成 m m m ( m ≥ 0 m \geq 0 m≥0) 个互不相交的集合，每个集合本身又是一棵树，被称为根的子树（SubTree）。

与数组（一对一）不同，树结构通过"一对多"的关系模拟了现实世界中的层级结构（如文件系统、组织架构）。

核心术语表：

术语	定义及图例说明
父结点/双亲结点	若一个结点含有子结点，则这个结点称为其子结点的父结点；
子结点/孩子结点	一个结点含有的子树的根结点称为该结点的子结点；
结点的度	一个结点有几个孩子，它的度就是多少；
树的度	一棵树中，最大的结点的度称为树的度；
叶子结点/终端结点	度为 0 的结点称为叶结点；
分支结点/非终端结点	度不为 0 的结点；
兄弟结点	具有相同父结点的结点互称为兄弟结点（亲兄弟）；
结点的层次	从根开始定义起，根为第 1 层，根的子结点为第 2 层，以此类推。
树的高度或深度	树中结点的最大层次；
结点的祖先	从根到该结点所经分支上的所有结点；
路径	一条从树中任意结点出发，沿父结点-子结点连接，达到任意结点的序列；
子孙	以某结点为根的子树中任一结点都称为该结点的子孙。
森林	由 m ( m > 0 ) m (m>0) m(m>0) 棵互不相交的树的集合称为森林。

1.3 树的复杂表示：孩子兄弟表示法

树不像二叉树那样每个节点只有两个叉，一个节点可能有 N N N 个孩子。如何存储？

最通用且优美的方法是 孩子兄弟表示法 （Left-Child Right-Brother Representation）。

c 复制代码

struct Node {
    int data;
    struct Node* child;    // 指向左边第一个孩子
    struct Node* brother;  // 指向右边的下一个亲兄弟
};

这种设计巧妙地将任意复杂的树转化为了二叉结构，便于统一处理。

二、二叉树------规则的艺术

2.1 二叉树的特殊规则

二叉树不是简单的度为2的树，它要求：

不存在度大于 2 的结点。
有序性：子树有左右之分，次序不能颠倒。

2.2 两种特殊的二叉树（堆的物理基础）

这是本教程最关键的理论部分，请务必区分：

满二叉树 (Full Binary Tree) ：
- 定义：每一层的结点数都达到最大值。
- 公式：深度为 k k k 的满二叉树，结点总数 N = 2 k − 1 N = 2^k - 1 N=2k−1。
完全二叉树 (Complete Binary Tree) ：
- 定义：深度为 k k k 的二叉树，前 k − 1 k-1 k−1 层是满的，第 k k k 层（最后一层）的结点从左到右连续排列，中间没有空隙。
- 意义：完全二叉树是效率极高的数据结构，它是数组存储二叉树的最佳形态。

2.3 二叉树的重要性质

对于任意二叉树，如果度为 0 的叶结点个数为 n 0 n_0 n0，度为 2 的分支结点个数为 n 2 n_2 n2，则有：

n 0 = n 2 + 1 n_0 = n_2 + 1 n0=n2+1

即：叶子永远比分叉多的结点多一个。这一性质常用于快速计算节点数量。

三、从逻辑到物理------堆的数组映射

3.1 为什么堆使用顺序存储？

二叉树通常用链表存储（二叉链表），包含 left 和 right 指针。

但是，对于完全二叉树，我们可以使用数组（顺序结构）存储，且不会有任何空间浪费。

堆（Heap），本质上就是一棵采用数组存储的完全二叉树。

3.2 下标映射公式

假设我们将完全二叉树的节点从上到下、从左到右依次存入数组 a 中，且下标从 0 开始：

父节点找子节点 ：
- 如果父节点索引为 i i i
- 左孩子索引 ： L e f t C h i l d = 2 × i + 1 LeftChild = 2 \times i + 1 LeftChild=2×i+1
- 右孩子索引 ： R i g h t C h i l d = 2 × i + 2 RightChild = 2 \times i + 2 RightChild=2×i+2
子节点找父节点 ：
- 如果子节点索引为 i i i（无论左右）
- 父节点索引 ： P a r e n t = ( i − 1 ) / 2 Parent = (i - 1) / 2 Parent=(i−1)/2 （整数除法，向下取整）

这个公式是堆算法高效运行的核心引擎。

复制代码

       逻辑结构(树)                物理结构(数组)
           10 (idx:0)
         /    \                  -------------------------------------
       15      30                | 10 | 15 | 30 | 40 | 50 | 100 | 70 |
      /  \    /  \               -------------------------------------
    40   50 100  70          idx:   0    1    2    3    4    5    6

    验证公式：
    节点 15 的索引是 1。
    其左孩子 40：2*1 + 1 = 3 (正确)
    其父节点 10：(1-1) / 2 = 0 (正确)

3.3 堆的定义

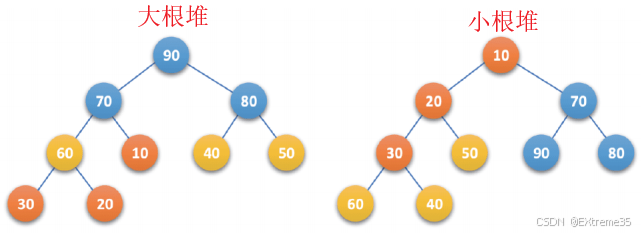
堆，本质上就是一棵满足特定排序规则的完全二叉树。根据排序规则的不同，分为两类：

小根堆 (Min Heap) ： K i ≤ K 2 i + 1 K_i \le K_{2i+1} Ki≤K2i+1 且 K i ≤ K 2 i + 2 K_i \le K_{2i+2} Ki≤K2i+2。即任意父节点 ≤ \le ≤ 子节点，堆顶是最小值。
大根堆 (Max Heap) ： K i ≥ K 2 i + 1 K_i \ge K_{2i+1} Ki≥K2i+1 且 K i ≥ K 2 i + 2 K_i \ge K_{2i+2} Ki≥K2i+2。即任意父节点 ≥ \ge ≥ 子节点，堆顶是最大值。

注意：堆只保证"父子"有序，不保证"兄弟"有序。左孩子可能比右孩子大，也可能小。

为什么需要堆？ 你可能会问："如果我要找最小值，遍历数组不行吗？"

数据结构	插入 (Insert)	删除堆顶 (Pop)	获取堆顶 (Top)
有序数组	O ( N ) O(N) O(N) (需移动元素)	O ( 1 ) O(1) O(1) (尾删) / O ( N ) O(N) O(N) (头删)	O ( 1 ) O(1) O(1)
无序数组	O ( 1 ) O(1) O(1)	O ( N ) O(N) O(N) (需遍历找最值)	O ( N ) O(N) O(N)
堆 (Heap)	O ( log ⁡ N ) O(\log N) O(logN)	O ( log ⁡ N ) O(\log N) O(logN)	O ( 1 ) O(1) O(1)

堆在"插入"和"删除"之间取得了完美的平衡，是插入与查找性能平衡的艺术大师。

四、堆的底层原理与核心算法

堆的运作依赖两个核心算法：上浮（Shift Up） 和 下沉（Shift Down） 。所有的 API（Push, Pop）本质上都是对这两个算法的封装。

数据结构定义如下：

c 复制代码

typedef int HDataType; // 方便后续一键替换为 float 或结构体

typedef struct Heap
{
	HDataType* a;  // 指向动态分配的数组
	int size;      // 有效数据个数（也是下一个插入位置的下标）
	int capacity;  // 数组当前的总容量
} HP;

4.1 核心算法一：上浮 (AdjustUP)

场景：当我们向堆中插入一个新元素时。

策略：我们将新元素放在数组的末尾（维持完全二叉树结构），但这可能会破坏堆序性（例如，在小根堆里插入了一个极小值）。因此，我们需要让这个新元素"上浮"到合适的位置。

步骤：

比较当前节点与父节点。
若 当前节点 < 父节点（小根堆规则），则交换两者。
将当前位置更新为父节点位置，重复步骤1。
若 当前节点 >= 父节点，或已到达根节点（索引0），停止。

c 复制代码

// 向上调整：确保子节点 >= 父节点
void AdjustUP(HDataType* a, int child)
{
	int parent = (child - 1) / 2; // 计算父节点
	
	while (child > 0) // 循环直到根节点
	{
		// 小根堆逻辑：若孩子比父亲小，交换
		if (a[parent] > a[child])
		{
			swap(&(a[parent]), &(a[child]));
			child = parent; // 向上爬一层
			parent = (child - 1) / 2;
		}
		else
		{
			break; // 满足堆序，停止
		}
	}
}

4.2 核心算法二：下沉 (AdjustDown)

当我们删除堆顶元素时。

直接删除堆顶会破坏树结构（变成两棵树）。
巧妙做法 ：将堆顶元素与堆尾元素交换，然后直接删除堆尾（操作数组大小减1）。
此时，新的堆顶元素（原堆尾）通常很大，破坏了小根堆性质。我们需要让它"下沉"。

步骤：

从当前节点（初始为根）开始，找到其左右孩子中较小的那个（对于小根堆）。
若 当前节点 > 较小的孩子，则交换两者。
更新当前节点为该孩子节点的位置，重复步骤1。
若 当前节点 <= 较小的孩子，或没有子节点，停止。

c 复制代码

void AdjustDown(HDataType* a, int n, int parent)
{
	// 1. 预判左孩子
	int child = parent * 2 + 1;
	
	while (child < n) // 只要还有孩子
	{
		// 2. 选出左右孩子中更小的那个
        // 必须先判断 child+1 < n 确保右孩子存在
		if (child + 1 < n && a[child] > a[child + 1])
		{
			child++; // 右孩子更小，child 指向右孩子
		}

		// 3. 父节点与较小孩子比较
		if (a[parent] > a[child])
		{
			swap(&(a[parent]), &(a[child]));
			parent = child; // 继续向下沉
			child = parent * 2 + 1;
		}
		else
		{
			break; // 位置正确
		}
	}
}

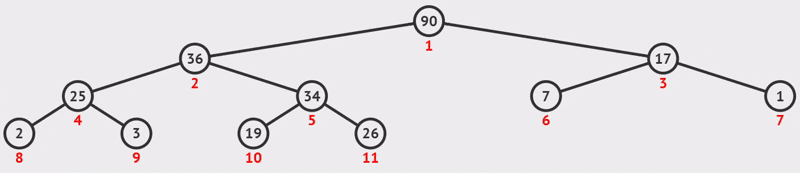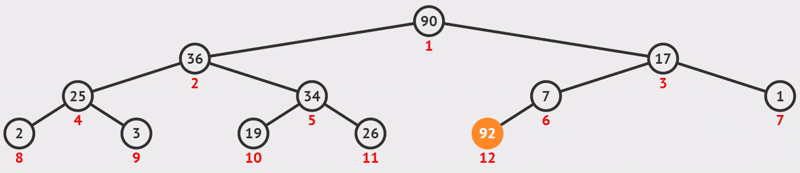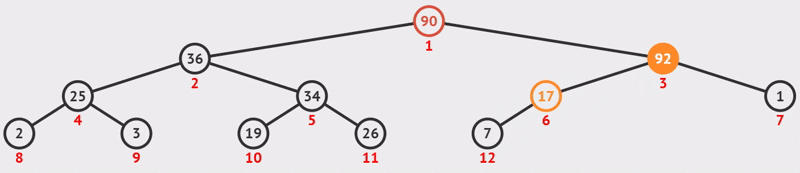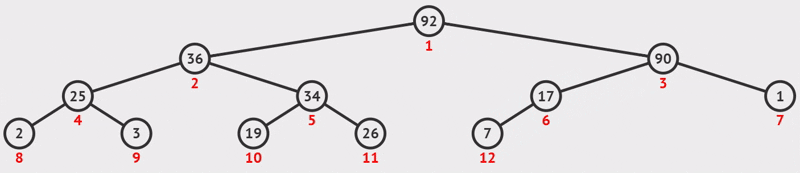
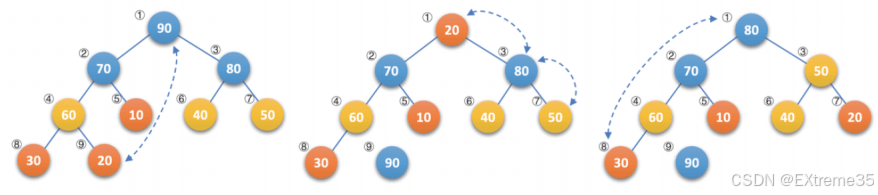
例如下图所示，图1是一个大顶堆 ，90为最大值，将90与20(末尾元素)互换，如图2所示，此时90就成了整个堆序列的最后一个元素，也就是逻辑删除，将20经过下沉调整，使得除90以外的结点继续满足大顶堆定义(所有结点都大于等于其孩子)，见图3，然后再考虑将30与80互换......

五、堆的高级应用

5.1 堆排序 (Heap Sort)

堆排序的精髓在于利用堆顶的最值特性。

建堆：使用 AdjustDown 从最后一个非叶子节点开始调整，复杂度 O ( N ) O(N) O(N)。
排序：不断交换堆顶与堆尾，缩小堆范围，并下沉堆顶。复杂度 O ( N log ⁡ N ) O(N \log N) O(NlogN)。

5.2 Top-K 问题（海量数据处理）

面试必问：如何在 100 亿个整数中找到最大的 K K K 个数？

方案：

取前 K K K 个元素建立一个小根堆。
遍历剩余元素，若 当前元素 > 堆顶，则替换堆顶，并执行 AdjustDown。
遍历结束后，堆中剩余的 K K K 个元素即为最大的 K K K 个。

为什么求最大值要用小根堆？

因为小根堆的堆顶是当前 K K K 个数中的"门槛"。只有比门槛大的数才有资格进入，进入后门槛可能会提高（下沉调整）。

六、结语

从树的递归定义，到二叉树的数学性质，再到堆的数组实现，我们看到数据结构是如何在空间与时间之间寻找平衡的。

满二叉树 是理论的完美。
完全二叉树 是工程的妥协与高效。
堆则是利用这种结构特性解决最值问题的神兵利器。

掌握了 AdjustUp 和 AdjustDown，你不仅学会了堆，更打开了优先队列、堆排序以及海量数据处理的大门。

【数据结构】打破线性思维：树形结构与堆在C语言中的完美实现方案

目录

从树到堆：C语言数据结构深度实战教程

一、树------非线性结构的基石

1.1 树的严谨定义

1.2 树的定义与术语

1.3 树的复杂表示：孩子兄弟表示法

二、二叉树------规则的艺术

2.1 二叉树的特殊规则

2.2 两种特殊的二叉树（堆的物理基础）

2.3 二叉树的重要性质

三、从逻辑到物理------堆的数组映射

3.1 为什么堆使用顺序存储？

3.2 下标映射公式

3.3 堆的定义

四、堆的底层原理与核心算法

4.1 核心算法一：上浮 (AdjustUP)

4.2 核心算法二：下沉 (AdjustDown)

五、堆的高级应用

5.1 堆排序 (Heap Sort)

5.2 Top-K 问题（海量数据处理）

六、结语