1 论文简介
《基于最大类间方差的最大熵图像分割》是由易三莉等人于 2018 年发表在《计算机工程与科学》上的一篇论文。该论文针对图像分割中最大熵算法对目标与背景界限模糊的图像分割效果较好但边缘识别能力差,以及最大类间方差算法边缘识别强但对界限模糊图像分割效果不佳的问题,提出了一种创新的结合方法。核心方法包括三个步骤:首先,应用二维最大类间方差算法对原图像进行初次分割,以有效提取边缘信息;其次,将初次分割结果与原图像通过加权结合,生成边缘增强的结合图像;最后,使用二维最大熵算法对结合图像进行最终分割。该方法还引入了二维直方图技术来改善抗噪性能,并利用积分图算法实现快速阈值选取。实验在多种自然图像上进行,结果显示该算法在分割准确率和边缘识别方面均优于传统的二维最大类间方差、二维最大熵和灰度-梯度熵算法,平均分割准确率达到 98.46%,标准差为 1.16%,表明其具有更高的有效性和鲁棒性。该算法被广泛应用于计算机视觉、模式识别和医学图像处理等领域,为解决复杂图像分割问题提供了有效方案,并在相关研究中显示出重要的影响力。
2 算法原理
假设图像大小为 M×NM \times NM×N,灰度级为 LLL,归一化直方图为 H=h0,h1,⋯ ,hL−1H = {h_0, h_1, \cdots, h_{L-1}}H=h0,h1,⋯,hL−1,其中 hih_ihi 表示灰度级 iii 的像素出现概率。整个算法结合最大类间方差的边缘识别和最大熵的均匀分布优势,实现高效图像分割。
2.1 步骤1:构建二维直方图
对于图像中每个像素点 (x,y)(x, y)(x,y),计算其 K×KK \times KK×K 邻域的平均灰度值 gmean(x,y)g_{\text{mean}}(x, y)gmean(x,y)。公式如下: gmean(x,y)=1K×K∑i=1K∑j=1Kf(x+i,y+j)g_{\text{mean}}(x, y) = \frac{1}{K \times K} \sum_{i=1}^{K} \sum_{j=1}^{K} f(x+i, y+j)gmean(x,y)=K×K1i=1∑Kj=1∑Kf(x+i,y+j) 由灰度值 iii 和平均灰度值 jjj 构成二维直方图,点 (i,j)(i, j)(i,j) 的概率为: pij=fijM×Np_{ij} = \frac{f_{ij}}{M \times N}pij=M×Nfij 其中 fijf_{ij}fij 是出现频率,且满足: ∑i=0L−1∑j=0L−1pij=1\sum_{i=0}^{L-1} \sum_{j=0}^{L-1} p_{ij} = 1i=0∑L−1j=0∑L−1pij=1 此步骤将图像信息扩展至二维空间,增强抗噪能力。
2.2 步骤2:应用二维最大类间方差算法进行初次分割
设阈值 (s,t)(s, t)(s,t),将二维直方图划分为背景区域 C0C_0C0、目标区域 C1C_1C1,以及忽略的边缘和噪声区域 C2C_2C2 和 C3C_3C3。类间方差计算公式为: σSB=ω0[(μi0−μT)2+(μj0−μT)2]+ω1[(μi1−μT)2+(μj1−μT)2]\sigma S_B = \omega_0 [(\mu_{i0} - \mu_T)^2 + (\mu_{j0} - \mu_T)^2] + \omega_1 [(\mu_{i1} - \mu_T)^2 + (\mu_{j1} - \mu_T)^2]σSB=ω0[(μi0−μT)2+(μj0−μT)2]+ω1[(μi1−μT)2+(μj1−μT)2] 其中 ω0\omega_0ω0 和 ω1\omega_1ω1 分别为 C0C_0C0 和 C1C_1C1 的区域概率,μi0\mu_{i0}μi0、μj0\mu_{j0}μj0 是 C0C_0C0 的均值矢量分量,μi1\mu_{i1}μi1、μj1\mu_{j1}μj1 是 C1C_1C1 的均值矢量分量,μT\mu_TμT 是整体均值矢量。通过遍历所有可能的 (s,t)(s, t)(s,t),找到使 σSB\sigma S_BσSB 最大的阈值,进行初次分割得到图像 f1f_1f1。此步骤优先提取图像边缘。
2.3 步骤3:加权结合生成边缘增强图像
将初次分割图像 f1f_1f1 与原图像 fff 通过线性加权结合,公式为: f2=αf1+βff_2 = \alpha f_1 + \beta ff2=αf1+βf 其中 α\alphaα 和 β\betaβ 是可调参数(α>0\alpha > 0α>0, β>0\beta > 0β>0)。此步骤增强图像的边缘特性,为后续分割提供优化输入。
2.4 步骤4:应用二维最大熵算法进行最终分割
对结合图像 f2f_2f2 构建二维直方图,设阈值 (k,m)(k, m)(k,m),划分区域 D0D_0D0(背景)和 D1D_1D1(目标),忽略边缘和噪声区域。计算 D0D_0D0 和 D1D_1D1 的信息熵: P(D0)=∑i=1k∑j=1mpijP(D_0) = \sum_{i=1}^{k} \sum_{j=1}^{m} p_{ij}P(D0)=i=1∑kj=1∑mpij H(D0)=−∑i=1k∑j=1mpijP(D0)ln(pijP(D0))H(D_0) = -\sum_{i=1}^{k} \sum_{j=1}^{m} \frac{p_{ij}}{P(D_0)} \ln \left( \frac{p_{ij}}{P(D_0)} \right)H(D0)=−i=1∑kj=1∑mP(D0)pijln(P(D0)pij) H(D1)=−∑i=k+1L∑j=m+1Lpij1−P(D0)ln(pij1−P(D0))H(D_1) = -\sum_{i=k+1}^{L} \sum_{j=m+1}^{L} \frac{p_{ij}}{1 - P(D_0)} \ln \left( \frac{p_{ij}}{1 - P(D_0)} \right)H(D1)=−i=k+1∑Lj=m+1∑L1−P(D0)pijln(1−P(D0)pij) 总熵为: ψ(k,m)=H(D0)+H(D1)\psi(k, m) = H(D_0) + H(D_1)ψ(k,m)=H(D0)+H(D1) 通过遍历找到使 ψ(k,m)\psi(k, m)ψ(k,m) 最大的阈值,进行最终分割得到图像 f3f_3f3。此步骤确保对界限模糊区域的有效处理。
3 实验结果
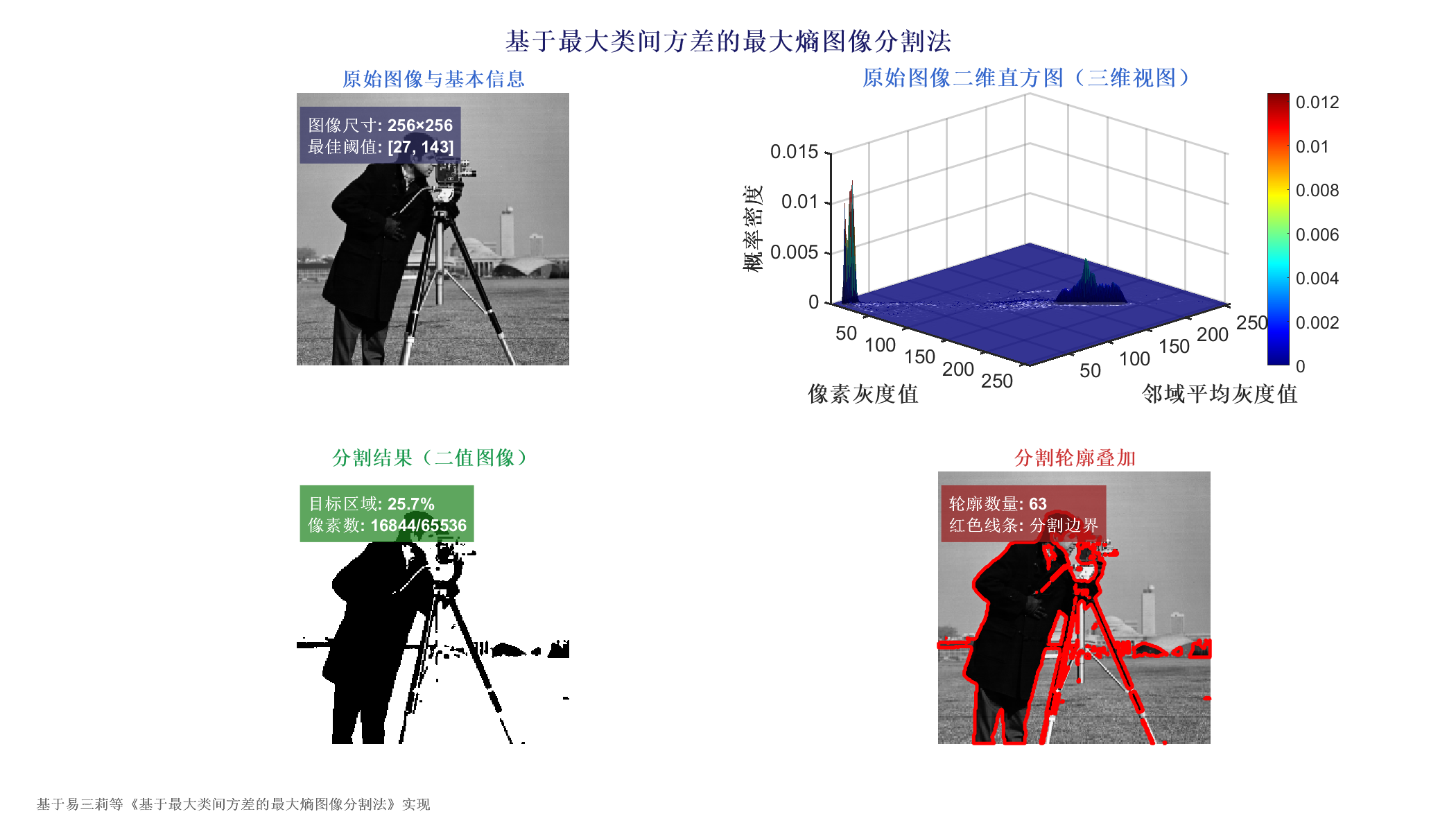
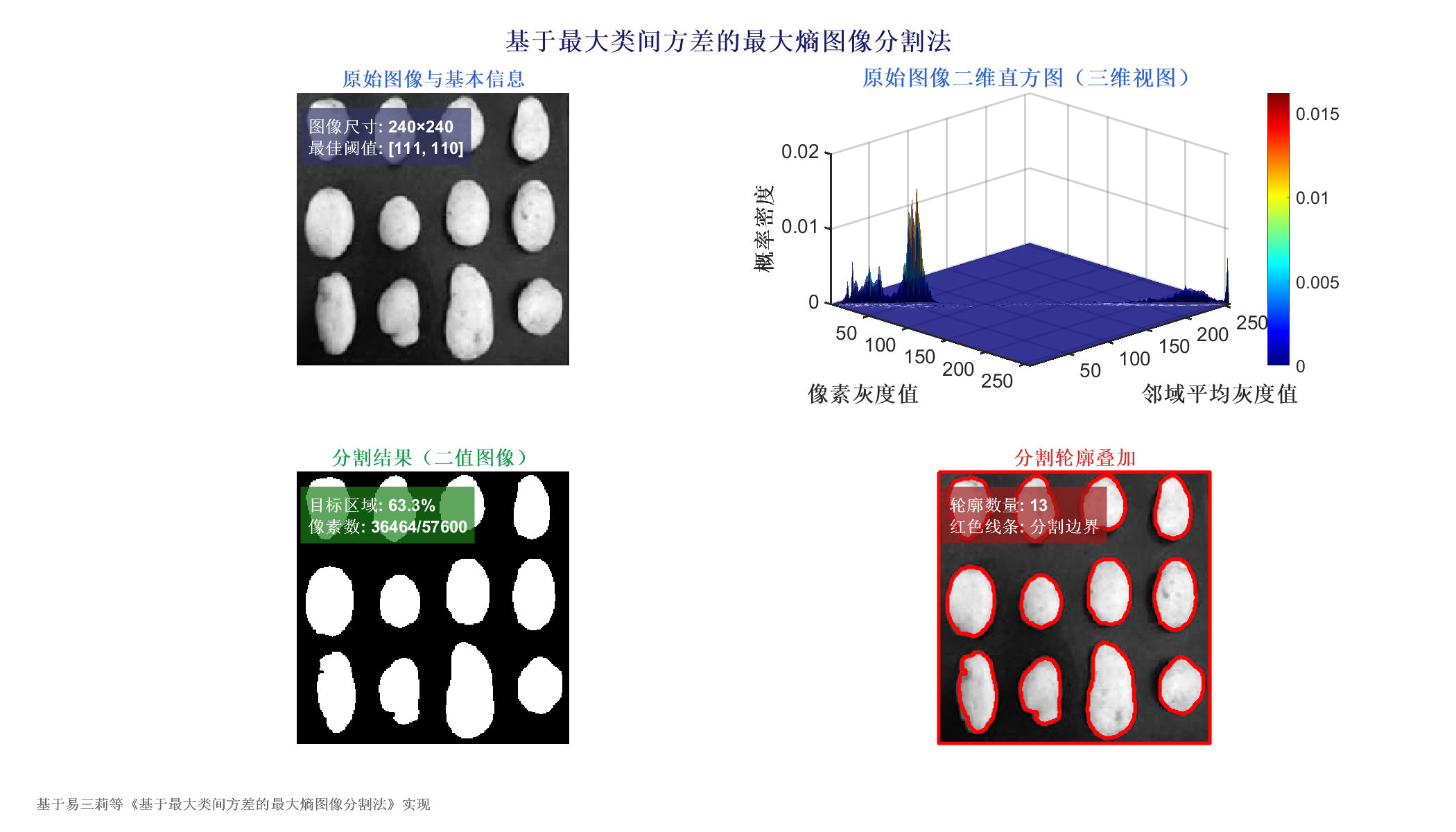
4 参考文献
1\] 易三莉, 张桂芳, 贺建峰, 等. 基于最大类间方差的最大熵图像分割\[J\]. 计算机工程与科学, 2018, 40(10):1874. ## 5 MATLAB 代码